Rotation angular motion angular momentom Physics 100 Chapt

Rotation, angular motion & angular momentom Physics 100 Chapt 6

Rotation

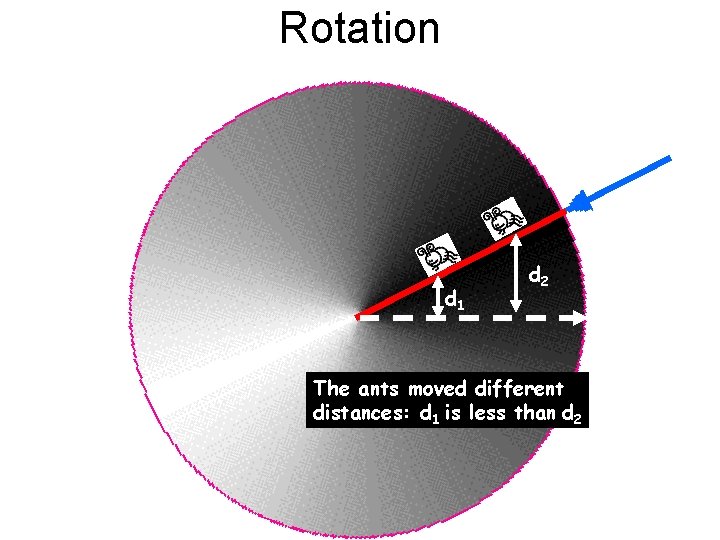
Rotation d 1 d 2 The ants moved different distances: d 1 is less than d 2

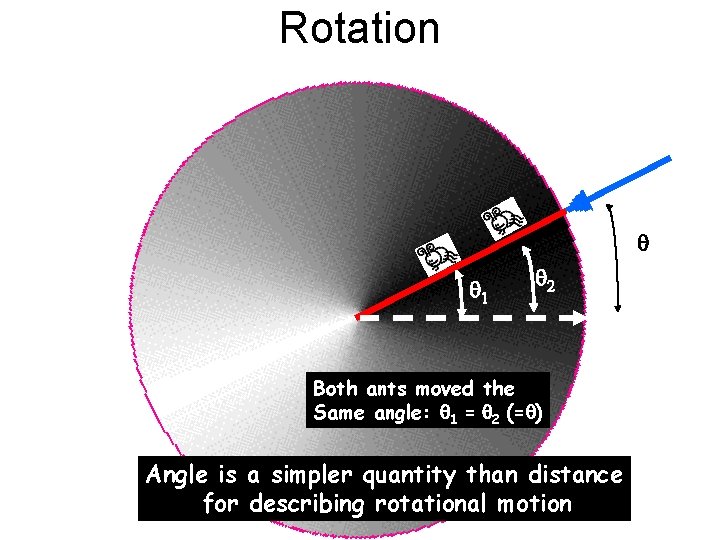
Rotation q q 1 q 2 Both ants moved the Same angle: q 1 = q 2 (=q) Angle is a simpler quantity than distance for describing rotational motion

Angular vs “linear” quantities Linear quantity distance velocity = change in d elapsed time symb. d v Angular quantity symb. angle angular vel. change in q = elapsed time q w

Angular vs “linear” quantities Linear quantity distance velocity acceleration = change in v elapsed time symb. d v a Angular quantity symb. angle q angular vel. w angular accel. a change in w = elapsed time

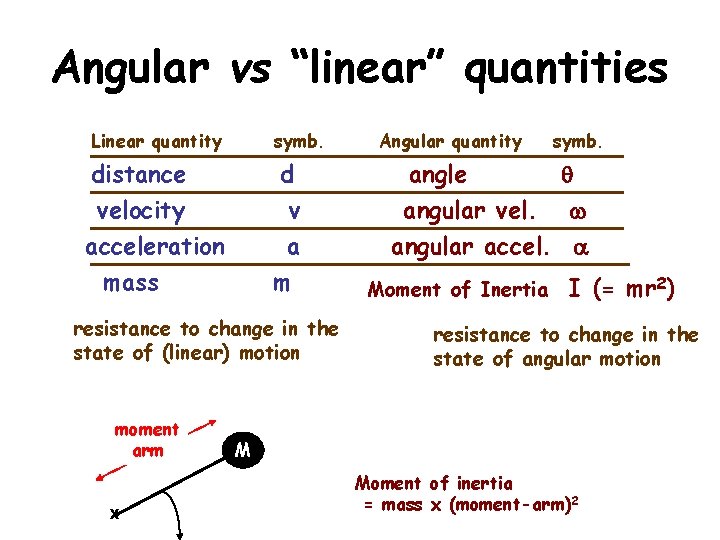
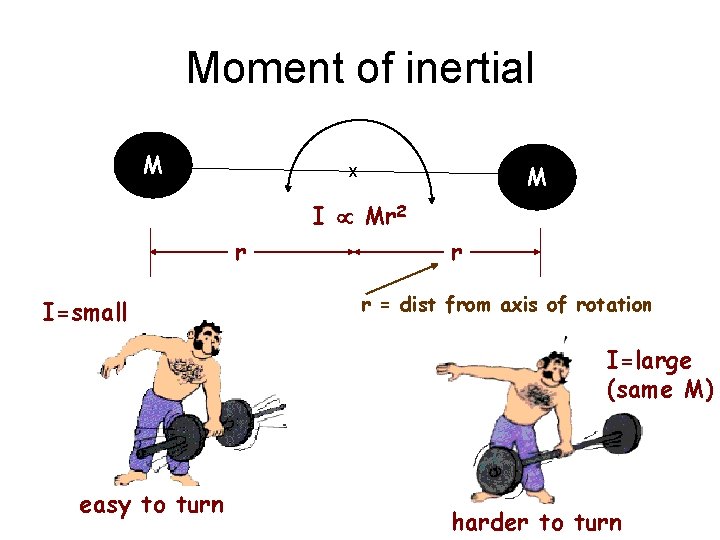
Angular vs “linear” quantities Linear quantity symb. distance velocity acceleration d v a mass m resistance to change in the state of (linear) motion moment arm x Angular quantity symb. angle q angular vel. w angular accel. a Moment of Inertia I (= mr 2) resistance to change in the state of angular motion M Moment of inertia = mass x (moment-arm)2

Moment of inertial M M x I Mr 2 r I=small r r = dist from axis of rotation I=large (same M) easy to turn harder to turn

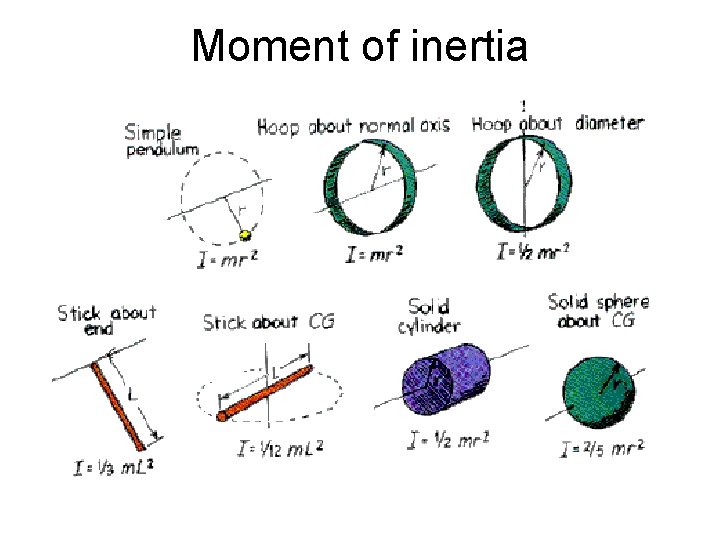
Moment of inertia

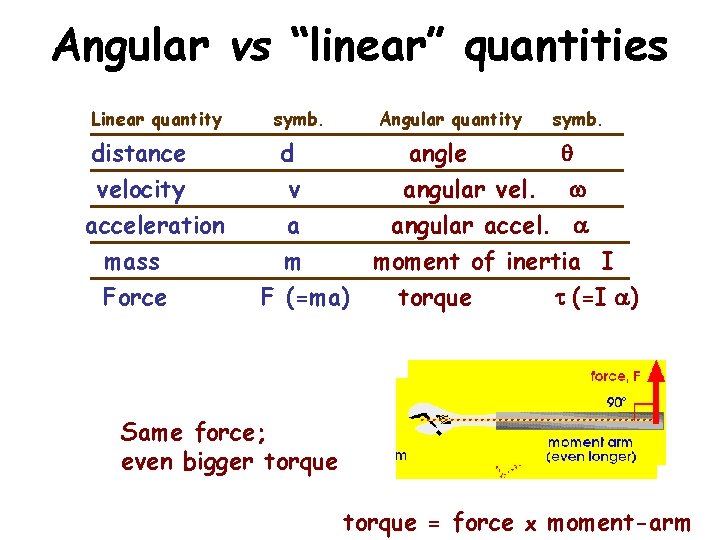
Angular vs “linear” quantities Linear quantity distance velocity acceleration mass Force symb. Angular quantity symb. d angle q v angular vel. w a angular accel. a m moment of inertia I F (=ma) torque t (=I a) Sameforce; Same bigger torque even bigger torque = force x moment-arm

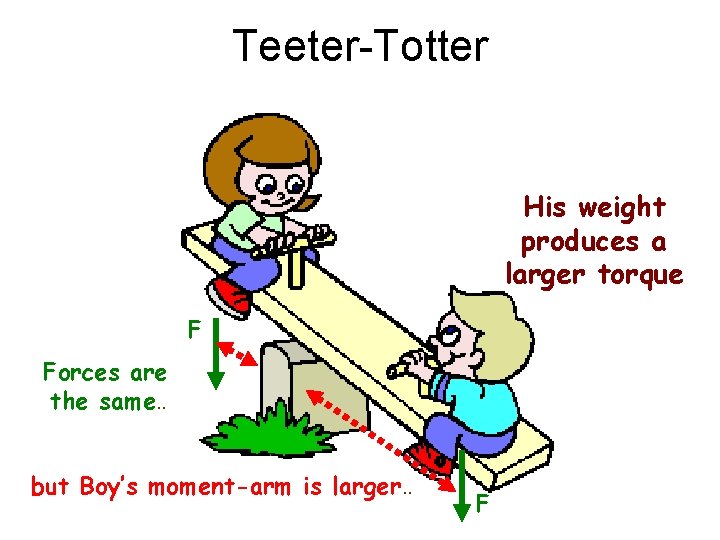
Teeter-Totter His weight produces a larger torque F Forces are the same. . but Boy’s moment-arm is larger. . F

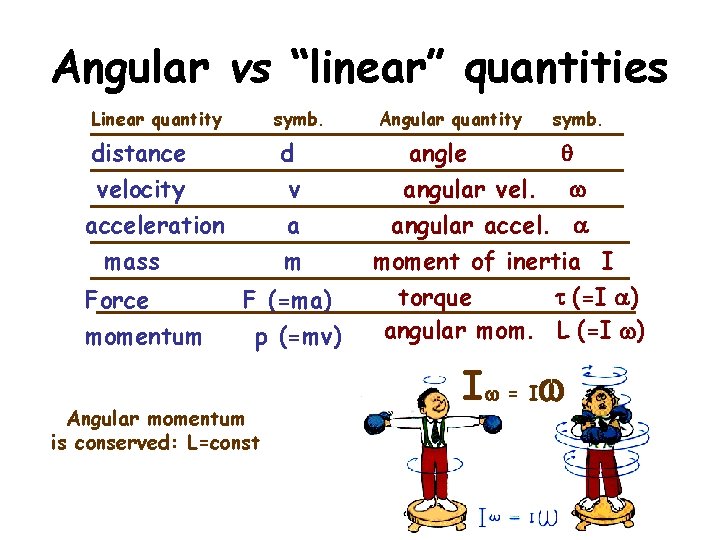
Angular vs “linear” quantities Linear quantity symb. distance velocity acceleration mass Force momentum d v a m F (=ma) p (=mv) Angular momentum is conserved: L=const Angular quantity symb. angle q angular vel. w angular accel. a moment of inertia I torque t (=I a) angular mom. L (=I w) I w = Iw

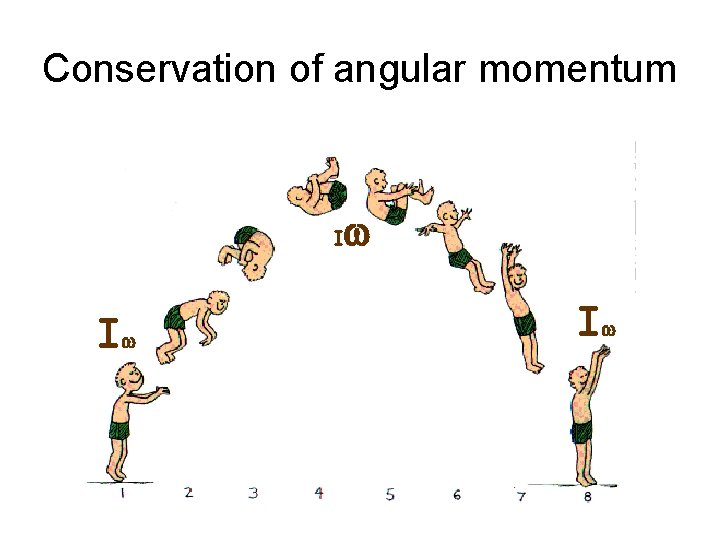
Conservation of angular momentum I Iw w Iw

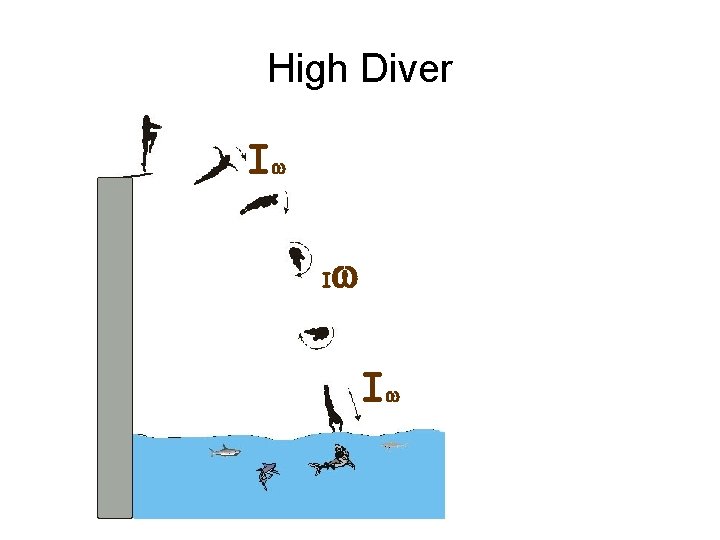
High Diver Iw I w Iw

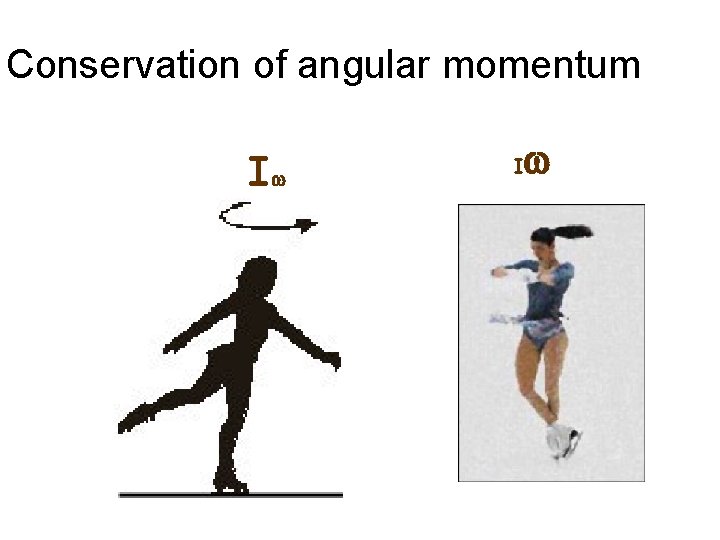
Conservation of angular momentum Iw I w

Angular momentum is a vector Right-hand rule

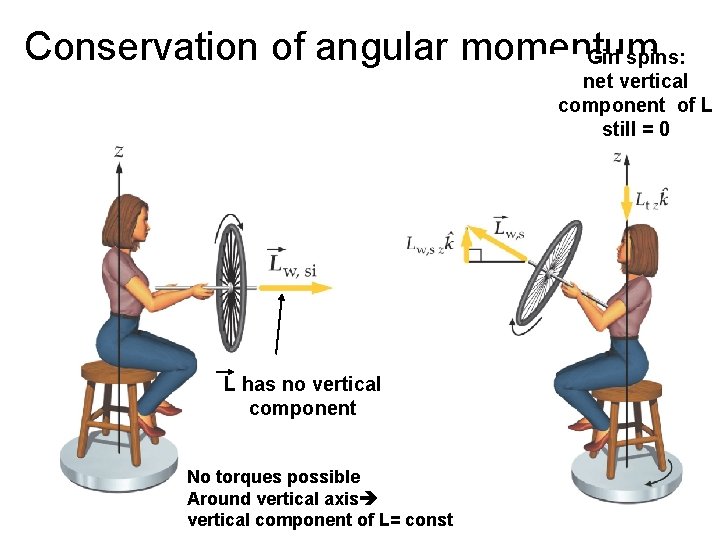
Conservation of angular momentum Girl spins: net vertical component of L still = 0 L has no vertical component No torques possible Around vertical axis vertical component of L= const

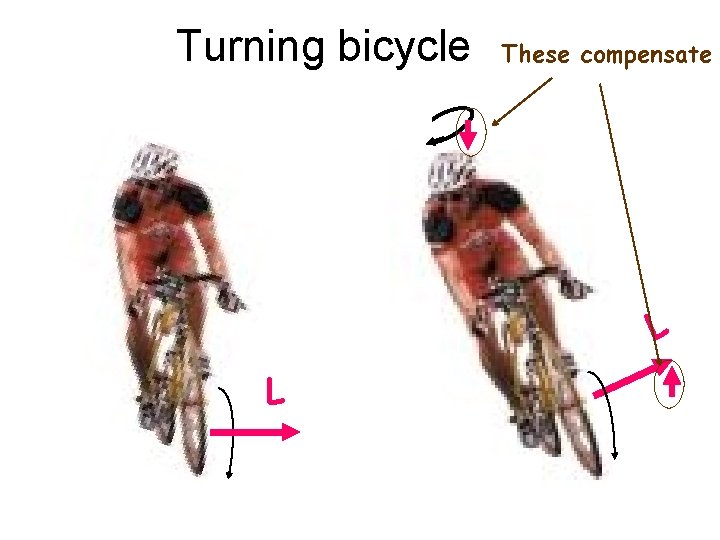
Turning bicycle These compensate L L

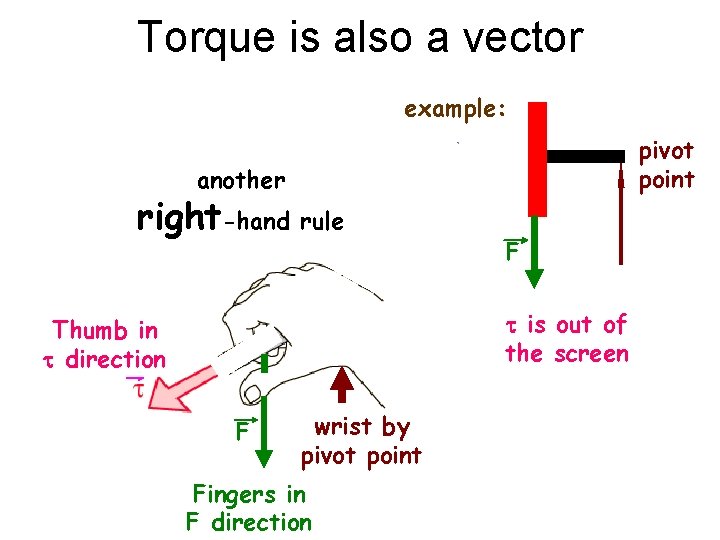
Torque is also a vector example: pivot point another right-hand rule F t is out of the screen Thumb in t direction F wrist by pivot point Fingers in F direction

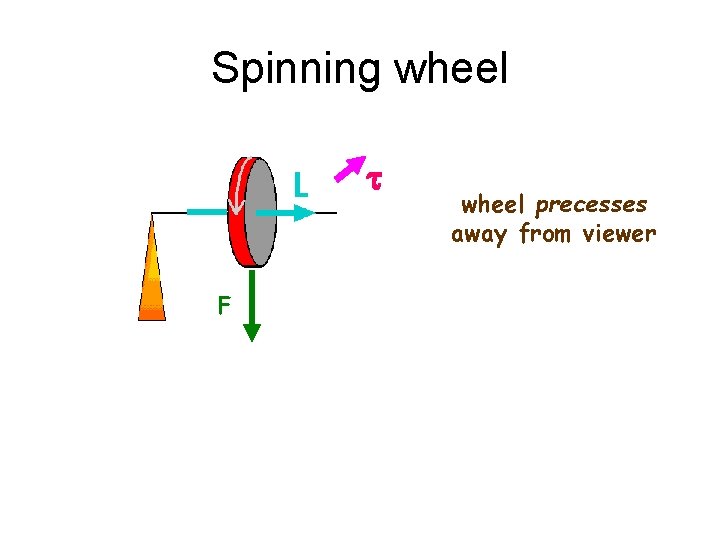
Spinning wheel t F wheel precesses away from viewer

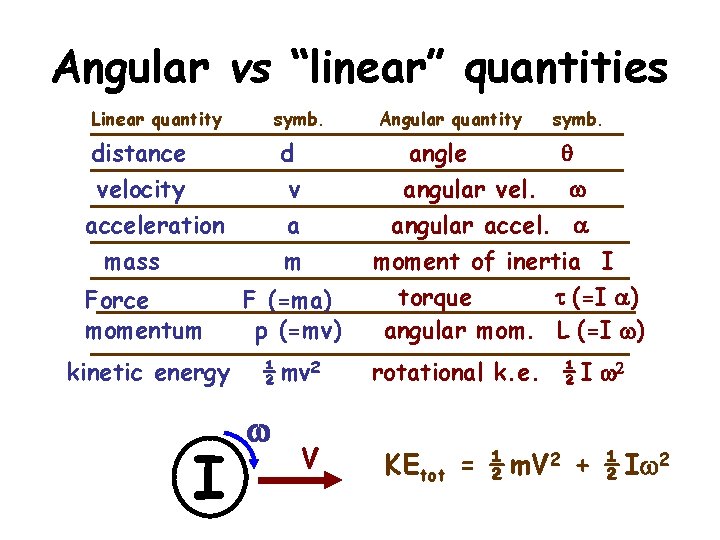
Angular vs “linear” quantities Linear quantity symb. distance velocity acceleration mass d v a m Force momentum F (=ma) p (=mv) kinetic energy ½ mv 2 I w V Angular quantity symb. angle q angular vel. w angular accel. a moment of inertia I torque t (=I a) angular mom. L (=I w) rotational k. e. ½ I w 2 KEtot = ½ m. V 2 + ½ Iw 2

Hoop disk sphere race

Hoop disk sphere race I I I

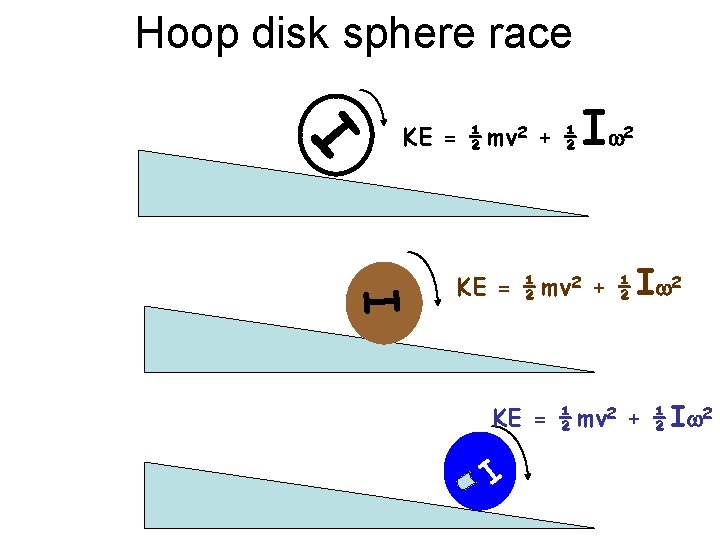
Hoop disk sphere race I KE = ½ mv 2 + ½ Iw 2 I

Hoop disk sphere race Every sphere beats every disk & every disk beats every hoop