Rotational Motion Torque and Angular Momentum AP Physics













- Slides: 21

Rotational Motion – Torque and Angular Momentum AP Physics 1

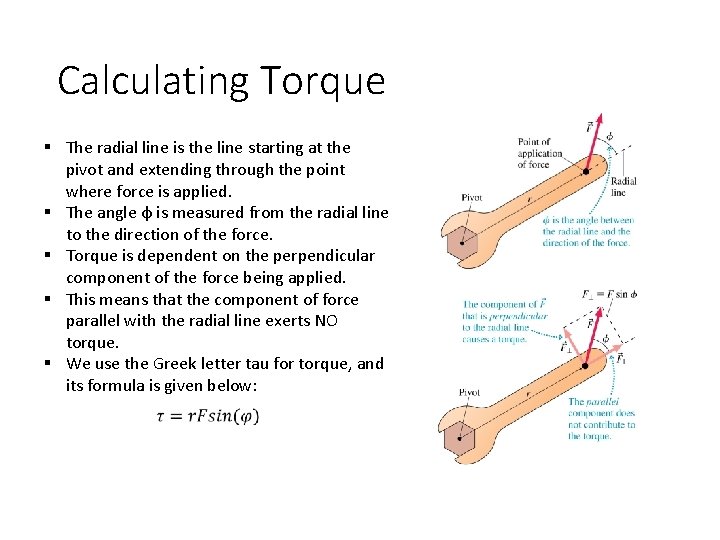
Torque § Forces with equal strength will have different effects on a swinging door. § The ability of a force to cause rotation depends on: § The magnitude F of the force. § The distance r from the pivot (the axis about which the object can rotate) to the point at which force is applied. § The angle at which force is applied. § This ability for a force to rotate something is called torque. § The units for torque are Nm (Newtonmeters).

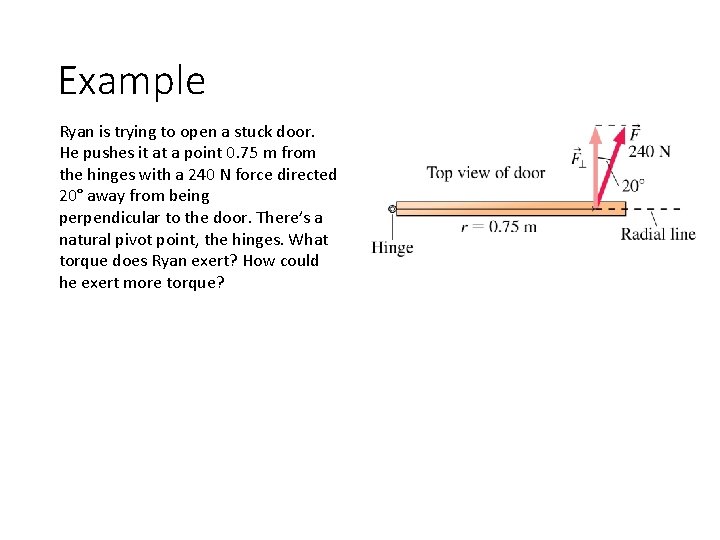
Calculating Torque § The radial line is the line starting at the pivot and extending through the point where force is applied. § The angle φ is measured from the radial line to the direction of the force. § Torque is dependent on the perpendicular component of the force being applied. § This means that the component of force parallel with the radial line exerts NO torque. § We use the Greek letter tau for torque, and its formula is given below:

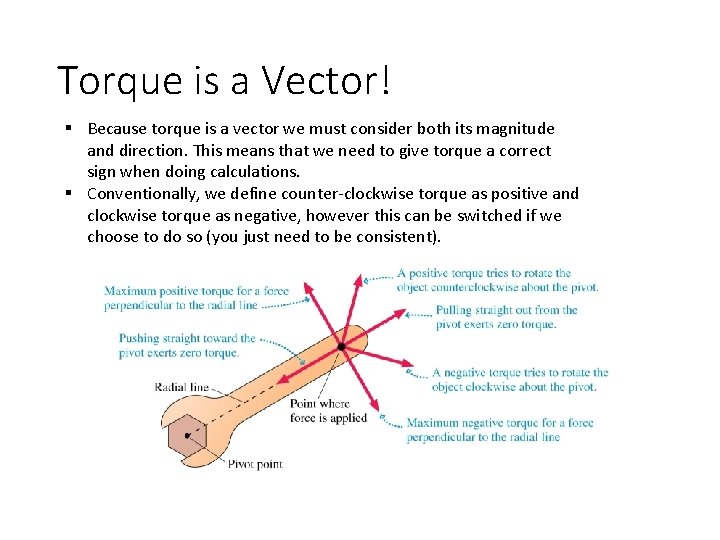
Example Ryan is trying to open a stuck door. He pushes it at a point 0. 75 m from the hinges with a 240 N force directed 20° away from being perpendicular to the door. There’s a natural pivot point, the hinges. What torque does Ryan exert? How could he exert more torque?

Torque is a Vector! § Because torque is a vector we must consider both its magnitude and direction. This means that we need to give torque a correct sign when doing calculations. § Conventionally, we define counter-clockwise torque as positive and clockwise torque as negative, however this can be switched if we choose to do so (you just need to be consistent).

Static Equilibrium § Often we will have more than one torques acting on an object. § In this case we can add these torques together (BE CAREFULL WITH DIRECTION!) to find our net torque. § If an object is at rest we can say that our net torque is equal to zero, meaning that all of our torques balance each other out. § Keep in mind that not every force exerts a torque! If a force does not provide a torque then it is not included in calculating net torque. § Forces that do not provide torques are still included when calculating net FORCE.

Example Suppose a 4600 kg elephant were placed on a see-saw with a 0. 025 kg mouse. The elephant is placed 10 meters from the point of rotation. How far from the point of rotation would the mouse need to be placed so that the system exists in a state of static equilibrium?

We missed something… § The plank itself had mass, and that means the force of gravity would be acting on it as well. This means that there is another torque that we would need to account for. § The question is where did that force act? § Technically, the force of gravity acts on every particle that makes up an object, but there is an easier way to view this force. § We will say that this force of gravity acts at a singular point, which we call the center of gravity, or center of mass.

Center of Mass § The center of mass of an object represents the average position of mass for an object or system. § The formula to calculate the center of mass for an object or system is given below. § This means that we would have to take every particle that makes up an object or system and multiply their masses with their positions, and then add all of these products together (and then divide by the total mass). Lets not do that. § The rigid bodies we will work with will be basic geometric shapes with a uniform density, so we can assume that the center of mass is located at the middle of the object. Yah symmetry!

Gravitational Torque § Gravitational torque is the torque that gravity exerts on an object. § If you are working a problem where things are balanced on a plank or there is a rod with stuff attached to it, be careful not to neglect the torque caused by the force of gravity on the plank or rod. § Side note: Sometimes problems will say that the mass of the plank is negligible, in this case we can consider the gravitational torque to equal 0.

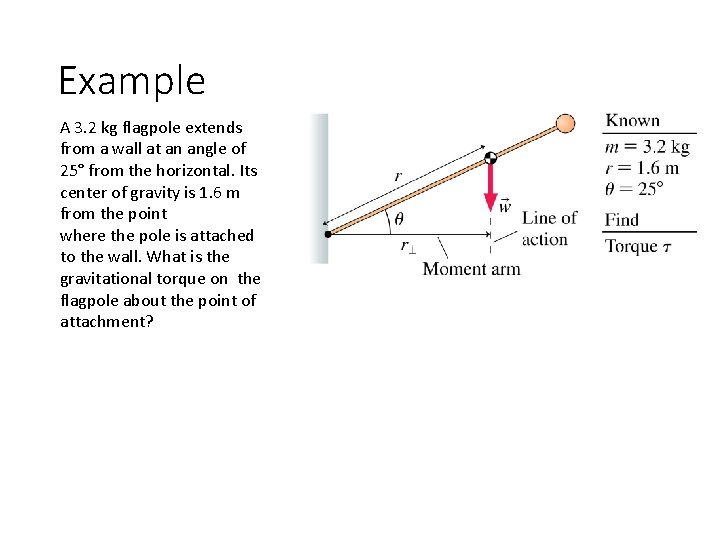
Example A 3. 2 kg flagpole extends from a wall at an angle of 25° from the horizontal. Its center of gravity is 1. 6 m from the point where the pole is attached to the wall. What is the gravitational torque on the flagpole about the point of attachment?

Rotational Dynamics § Many times torques will be acting on an object and the object will not be at static equilibrium. § We have seen that a net force causes an object to accelerate, which tells us that a net torque causes an object to experience angular acceleration! § In linear dynamics, we wrote out Newton’s second law with the formula: § In rotational dynamics (dynamics meaning that there is acceleration) this formula becomes: § Notice the similarities:

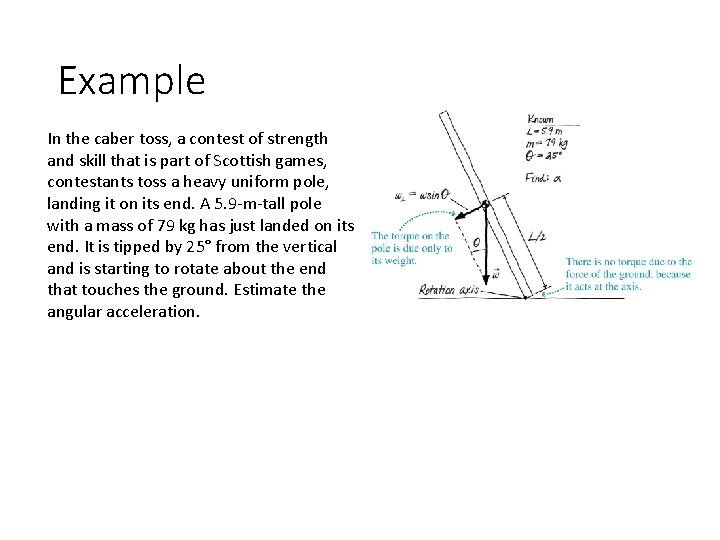
Example In the caber toss, a contest of strength and skill that is part of Scottish games, contestants toss a heavy uniform pole, landing it on its end. A 5. 9 -m-tall pole with a mass of 79 kg has just landed on its end. It is tipped by 25° from the vertical and is starting to rotate about the end that touches the ground. Estimate the angular acceleration.

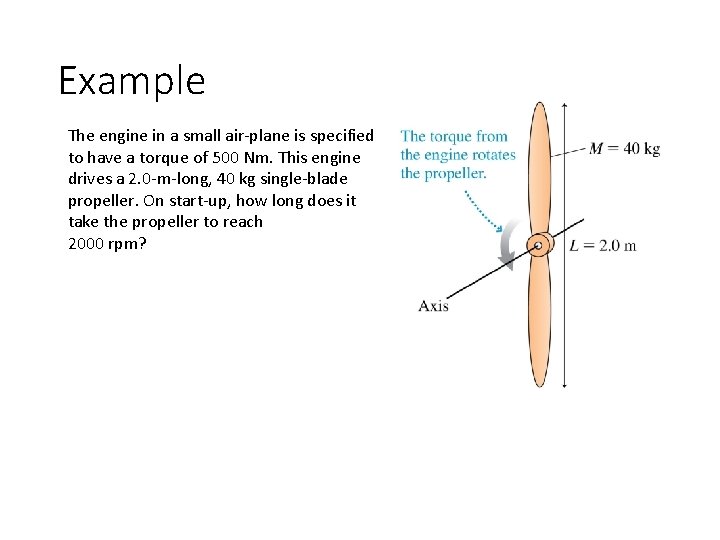
Example The engine in a small air-plane is specified to have a torque of 500 Nm. This engine drives a 2. 0 -m-long, 40 kg single-blade propeller. On start-up, how long does it take the propeller to reach 2000 rpm?

So I may have lied to you § In linear dynamics, we said if you lay a rope over a pulley, the tension is the same on both sides. This is only true if the pulley is MASSLESS. § If the pulley has mass, then it has a moment of inertia. If an object has a moment of inertia, it requires a net torque to get it rotating. § In order for us to have a net torque, one of our torques must be larger than the other. Because both tension forces act at the same distance from the rotational axis, one force must be larger than the other. § You still use Newton’s second law in the same way, you just cannot assume the tensions are the same anymore. § Side not: Sometimes the problem will say that the pulley is very light or massless, in that case you CAN say that the tensions are equal, but ONLY in that case.

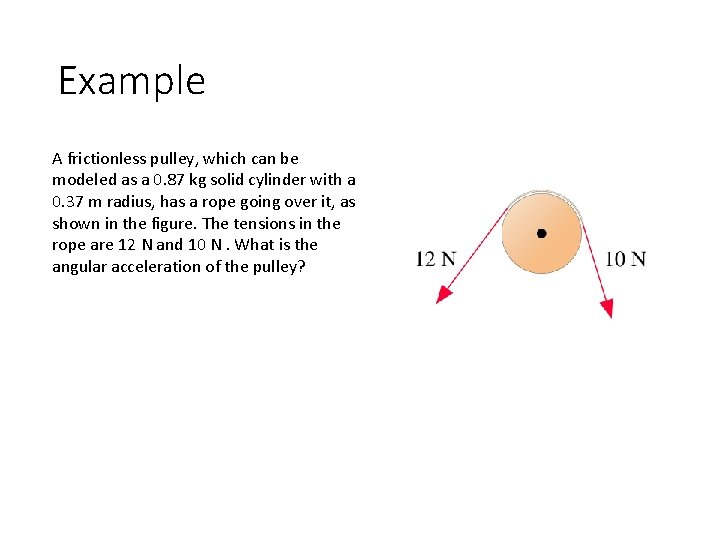
Example A frictionless pulley, which can be modeled as a 0. 87 kg solid cylinder with a 0. 37 m radius, has a rope going over it, as shown in the figure. The tensions in the rope are 12 N and 10 N. What is the angular acceleration of the pulley?

Angular Momentum § Momentum is not conserved for a spinning object because the direction of motion keeps changing. § Still, if it weren’t for friction, a spinning bicycle wheel would keep turning. § The quantity that expresses this idea for circular motion is called angular momentum. § Our variable for angular momentum is L. § The units for angular momentum are kg m/s 2. § The formula for the angular moment of a rotating rigid body is:

Angular Impulse-Momentum Theorem § In linear mechanics, we used Newton’s second law to show that a net force acting on a system changed the momentum of the system. § We can do the exact same thing in rotational mechanics by using Newton’s second law for rotation. In this case a net torque acting on a system changes the angular momentum of the system. The product of net torque and time is angular impulse.

Conservation of Angular Momentum § Using our equation for angular impulse, we can see that if there is no net torque acting on a system, the angular momentum of the system does not change. What does this mean? § Angular momentum is conserved! This can be used to explain various interesting occurrences, one of which is figure skating. § If a figure skater is spinning in a circle with their arms outstretched, they have angular momentum. § The skater brings their arms in, and they rotate faster. Angular momentum is conserved, and by bringing in their arms, their moment of inertia decrease. This means that their angular velocity has to increase!

Example An ice skater spins around on the tips of his blades while holding a 5. 0 kg weight in each hand. He begins with his arms straight out from his body and his hands 140 cm apart. While spinning at 2. 0 rev/s, he pulls the weights in and holds them 50 cm apart against his shoulders. If we neglect the mass of the skater, how fast is he spinning after pulling the weights in?

Conservation of Angular Momentum in Collisions § If an object strikes another object and makes it spin, we can conclude that there is angular momentum in the system and that it is conserved. § This is true even if neither object is rotating to begin with. § In the picture to the right the puck had angular momentum before the collision and both objects have angular momentum after the collision. § Because there is no torque on the system, the angular momentum is conserved. § The angular momentum of the puck is found by multiplying its linear momentum and the vertical position vector. § The vertical position vector is the distance between the point where the rod is hit and its rotational axis.