Angular and Linear Quantities Rotational Kinetic Energy Moment

-Angular and Linear Quantities -Rotational Kinetic Energy -Moment of Inertia AP Physics C Mrs. Coyle

Tangential (Linear) Speed and Angular Speed s=qr

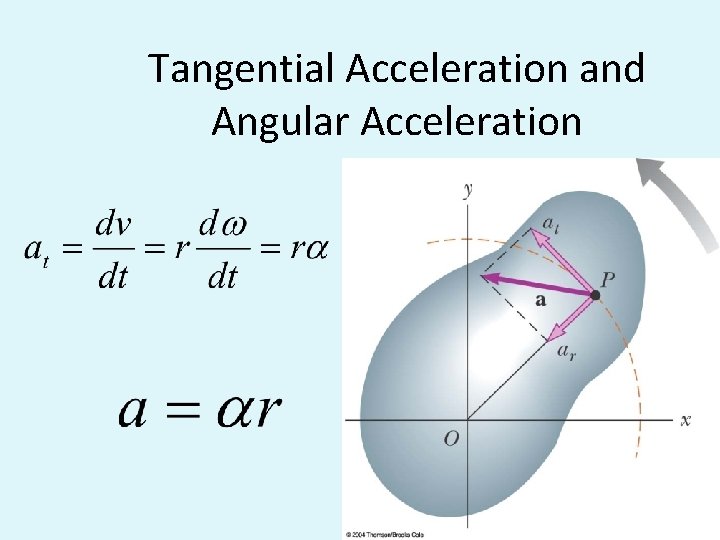
Tangential Acceleration and Angular Acceleration

Angular and Linear Quantities • Displacements • Speeds • Accelerations • Every point on the rotating object has the same angular motion but not the same linear motion. The a and v are functions of r.

Remember: Centripetal Acceleration v is the tangential speed

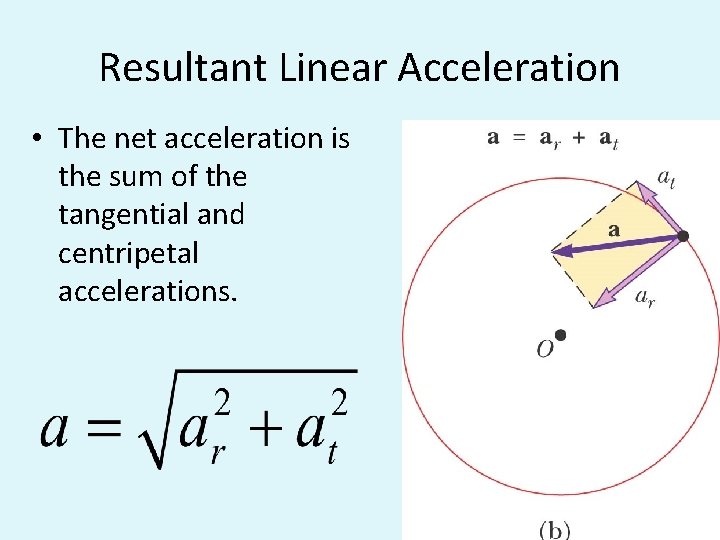
Resultant Linear Acceleration • The net acceleration is the sum of the tangential and centripetal accelerations.

Rotational Kinetic Energy • A particle in a rotating object has rotational kinetic energy: Ki = ½ mivi 2 , vi = wi r (tangential velocity) For the Object:

Rotational Kinetic Energy and Moment of Inertia • The total rotational kinetic energy of the rigid object is the sum of the energies of all its particles • I is called the moment of inertia

Moment of Inertia, I • Moment of Inertia, I, is a measure of the resistance of an object to changes in its rotational motion. • Moment of Inertia is analogous to mass in translational motion.

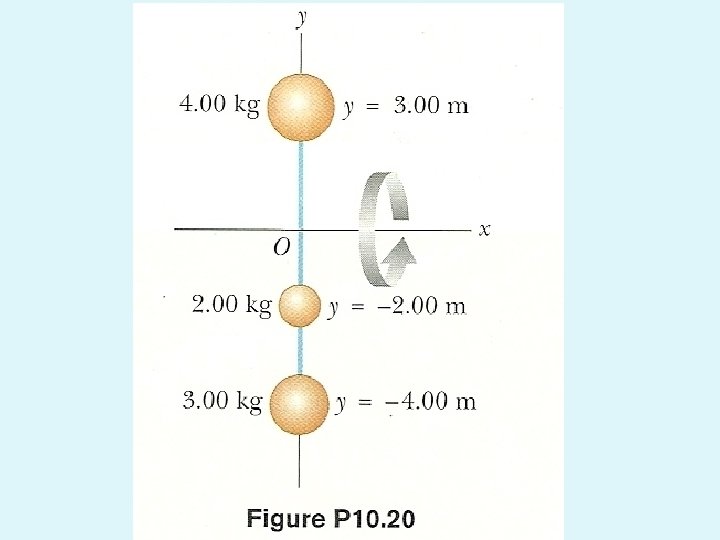
Example #20 Rigid rods of negligible mass lying along the y axis connect three particles. If the system rotates about the x-axis with an angular speed of 2. 00 rad/s find a) the moment of inertia about the x-axis and the total rotational kinetic energy evaluated from ½ I ω2 and b) the tangential speed of each particle and the total kinetic energy evaluated from ½ mi vi 2 Ans: a)92 kg m 2 , 184 J , b) 6 m/s, 4 m/s, 8 m/s, 184 J