Rotational KE Angular Momentum Rotational Energy l It












- Slides: 19

Rotational KE, Angular Momentum

Rotational Energy l It is moving so it is a type of Kinetic Energy (go back and rename the first) Translational KE Rotaional KE

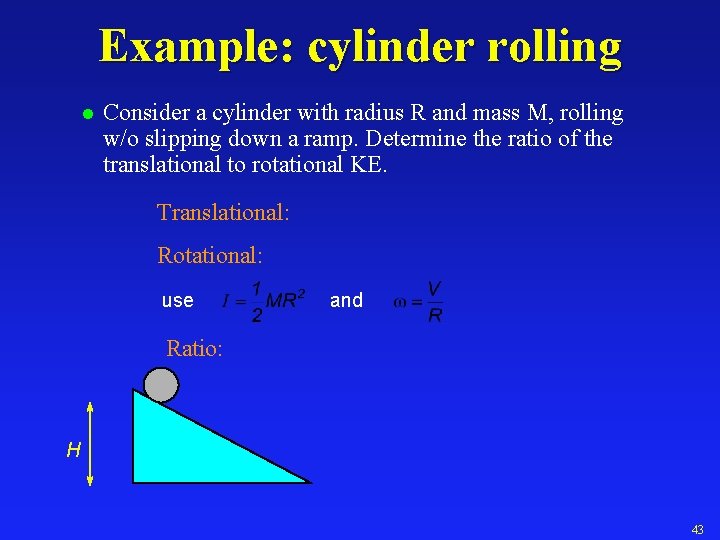
Example: cylinder rolling l Consider a cylinder with radius R and mass M, rolling w/o slipping down a ramp. Determine the ratio of the translational to rotational KE. Friction causes object to roll, but if it rolls w/o slipping friction does NO work! W = F d cos q H d is zero for point in contact No dissipated work, energy is conserved Need to include both translation and rotation kinetic energy. 43

Example: cylinder rolling l Consider a cylinder with radius R and mass M, rolling w/o slipping down a ramp. Determine the ratio of the translational to rotational KE. Translational: Rotational: use and Ratio: H 43

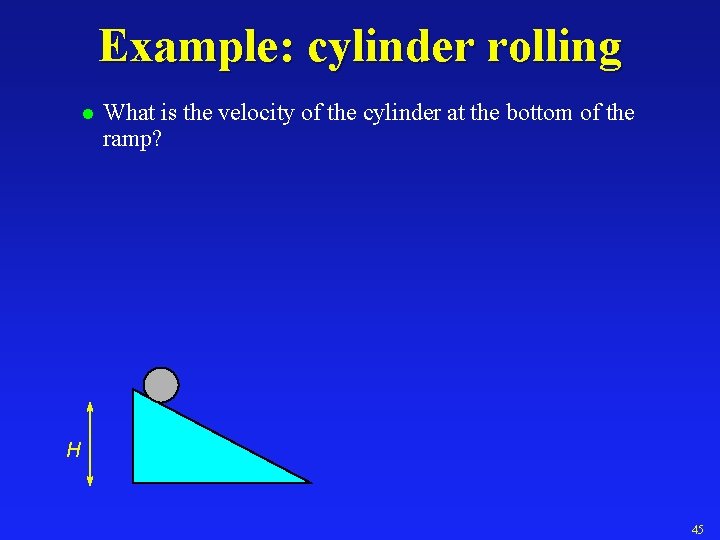
Example: cylinder rolling l What is the velocity of the cylinder at the bottom of the ramp? H 45

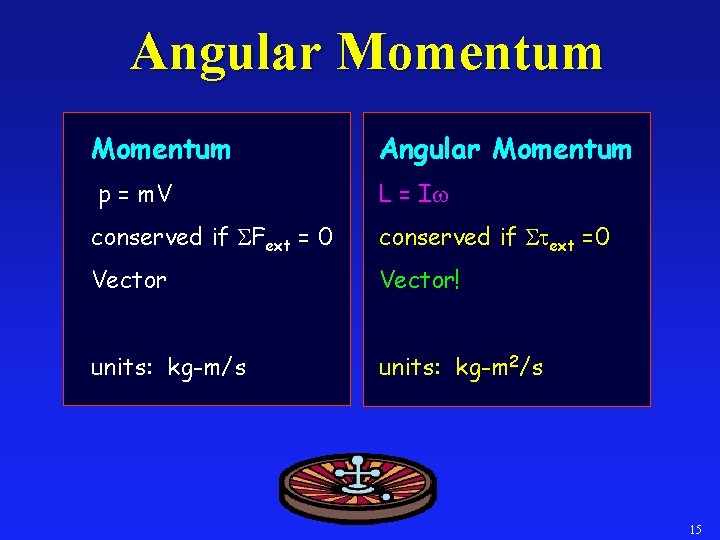
Angular Momentum p = m. V L = I conserved if Fext = 0 conserved if ext =0 Vector! units: kg-m/s units: kg-m 2/s 15

Direction of Angular Momentum l Right Hand Rule l Wrap fingers of right hand around direction of rotation, thumb gives direction of angular momentum.

Example: Two Disks l A disk of mass M and radius R rotates around the z axis with angular velocity i. A second identical disk, initially not rotating, is dropped on top of the first. There is friction between the disks, and eventually they rotate together with angular velocity f. Find f. z z i f 20

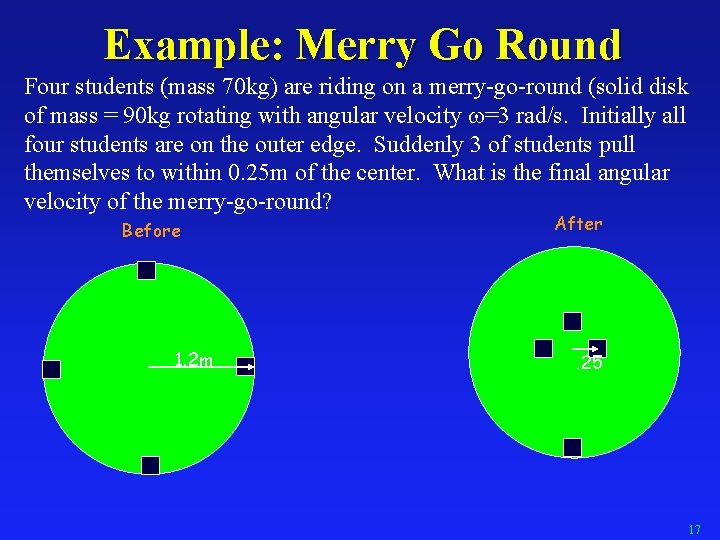
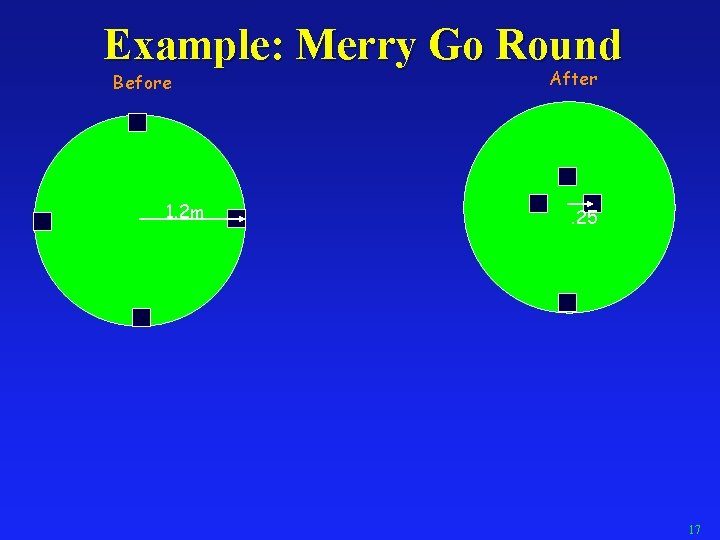
Example: Merry Go Round Four students (mass 70 kg) are riding on a merry-go-round (solid disk of mass = 90 kg rotating with angular velocity =3 rad/s. Initially all four students are on the outer edge. Suddenly 3 of students pull themselves to within 0. 25 m of the center. What is the final angular velocity of the merry-go-round? Before 1. 2 m After . 25 17

Example: Merry Go Round Before 1. 2 m After . 25 17

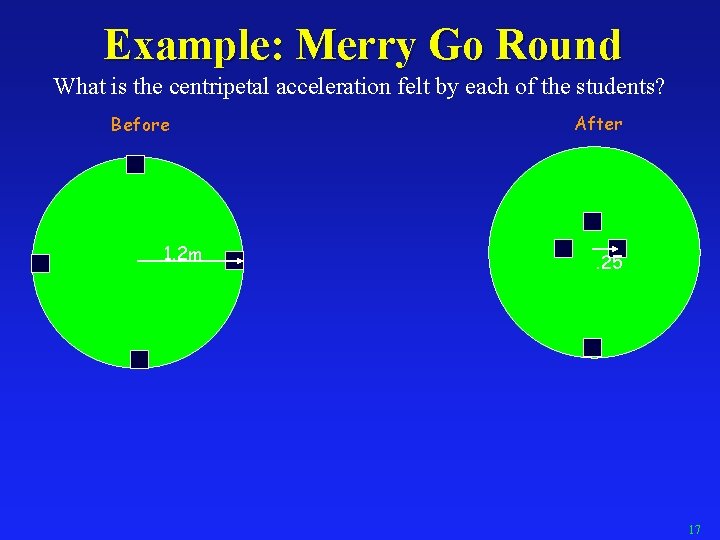
Example: Merry Go Round What is the centripetal acceleration felt by each of the students? Before 1. 2 m After . 25 17

Demo You are sitting on a freely rotating bar-stool with your arms stretched out and a weight in each hand. Your professor gives you a twist and you start rotating around a vertical axis though the center of the stool. You can assume that the bearing the stool turns on is frictionless, and that there is no net external torque present once you have started spinning. You now pull your arms and hands (and weights) close to your body. 22

Demo What happens to the angular momentum as you pull in your arms? 1. it increases 2. it decreases 3. it stays the same L L 1 2 What happens to your angular velocity as you pull in your arms? 1. it increases 2. it decreases 3. it stays the same 25

Demo What happens to your kinetic energy as you pull in your arms? 1. it increases 2. it decreases 3. it stays the same (using L = I ) 2 1 I 2 I 1 L L 29

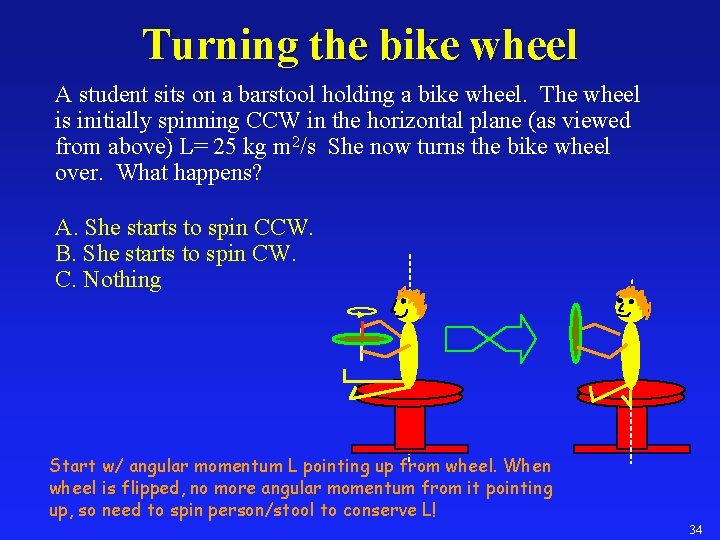
Turning the bike wheel A student sits on a barstool holding a bike wheel. The wheel is initially spinning CCW in the horizontal plane (as viewed from above) L= 25 kg m 2/s She now turns the bike wheel over. What happens? A. She starts to spin CCW. B. She starts to spin CW. C. Nothing Start w/ angular momentum L pointing up from wheel. When wheel is flipped, no more angular momentum from it pointing up, so need to spin person/stool to conserve L! 34

Gyroscopic Motion: l Suppose you have a spinning gyroscope in the configuration shown below: l If the left support is removed, what will happen? ? support pivot g 48

Gyroscopic Motion. . . l Suppose you have a spinning gyroscope in the configuration shown below: l If the left support is removed, what will happen? èThe gyroscope does not fall down! pivot g 45

Gyroscopic Motion. . . Bicycle wheel l. . . instead it precesses around its pivot axis ! pivot

Summary l l. L =Ia =I èRight Hand Rule gives direction èIf = 0, L is conserved