Rotational Motion Kinematics Moment of Inertia and Energy

















- Slides: 24

Rotational Motion – Kinematics, Moment of Inertia, and Energy AP Physics 1

Before we start § Up to this point, everything we have covered has been in regards to linear motion (except for circular motion). § Rotational motion will take all of these same ideas and apply them to rotating objects. § You will notice that all of our linear quantities (velocity, kinetic energy, force, ect…) have rotational counterparts. The formulas will have different variables, but they will be glued together the exact same way. § Use this to your advantage! Even though what we are about to do will look new, you have seen something very similar to it before.

Rotational Motion § Rotational motion is the motion of objects that spin about an axis. § We use the angle θ from the positive x-axis to describe the particle’s location. § Angle θ is the angular position of the particle. § Conventionally speaking, θ is positive when measured counterclockwise from the positive x-axis, and negative when measured clockwise from the positive x-axis.

Radians § We measure angle θ in the angular unit of radians, not degrees. § The radian is abbreviated “rad. ” § The arc length, s, is the distance that the particle has traveled along its circular path. § We define the particle’s angle θ in terms of arc length and radius of the circle: § Notice the angle an object rotates about when it travels a full circle: There are 2π radians in a full circle! Hooray Pre-Cal!

Angular Displacement § With linear motion, we calculated displacement of an object using the formula: § In rotation, we have a similar idea that we call angular displacement. This represents the number of radians an object is displaced through. § Again, these measurements must be made in RADIANS, not degrees.

Angular Velocity § The motion of an object moving in a straight line is often described by its velocity, which is the rate of change of the position of the object. § An object rotating in a circle has angular velocity, which represents the rate at which the angular position is changing. § Our units for angular velocity are rad/s. You may sometimes see this written as 1/s. § A common unit for angular velocity is RPM (revolutions per minute), you should convert this to rad/s before doing any calculations. § We can also relate period and frequency (which we discussed in SHM) to angular velocity:

Converting RPM to Rad/Second § It is important to understand how to convert from RPM to rad/s as many questions will give you angular velocities in units of RPM. Never use RPM in a problem, only rad/s! § To convert to rad/s we must use dimensional analysis. § There are 2π radians in 1 revolution. § We can see from this example that to go from RPM to rad/s, you simply need to multiply the angular speed in RPM by a factor of π/30.

Linear-Angular Velocity Relationship § We have said that a rotating object has an angular velocity, but the object still technically has a linear velocity. § Imagine a bike wheel spinning in a circle. If you mark a point on the wheel and spin it, the marked point has a velocity vector that is tangent to the path of the wheel. § We can use our expression for angle from earlier to relate the linear and angular velocity of an object. Dividing both sides by Δt This shows that an object that is spinning farther away from its rotational axis is actually traveling at a higher linear velocity!

Example The diameter of an audio compact disk is 12. 0 cm. When the disk is spinning at its maximum rate of 540 rpm, what is the speed of a point a. at a distance 3. 0 cm from the center and 1. 7 m/s b. at the outside edge of the disk, 6. 0 cm from the center? 3. 4 m/s

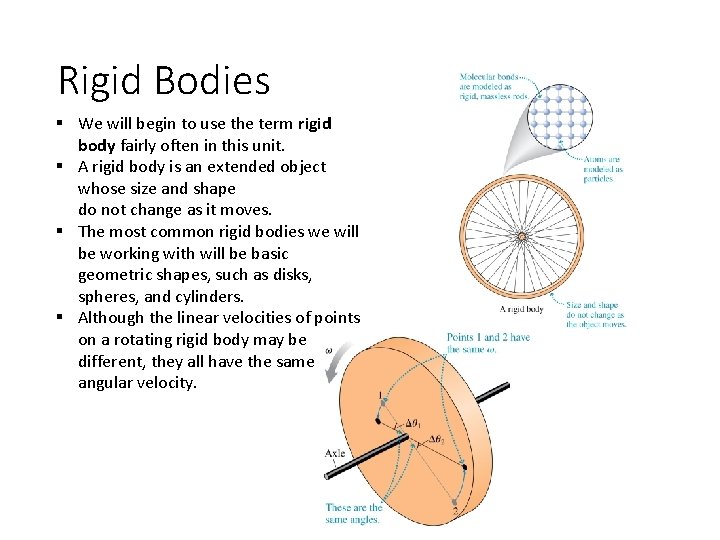
Rigid Bodies § We will begin to use the term rigid body fairly often in this unit. § A rigid body is an extended object whose size and shape do not change as it moves. § The most common rigid bodies we will be working with will be basic geometric shapes, such as disks, spheres, and cylinders. § Although the linear velocities of points on a rotating rigid body may be different, they all have the same angular velocity.

Angular Acceleration § In linear motion we said that a change in velocity for an object meant that it was accelerating. § A rotating object can also undergo a change in angular velocity. We call this angular acceleration. § The unit for angular acceleration is rad/s 2. § We can use the same method as before to show the relationship between linear and angular acceleration. Keep in mind that this is acceleration that is tangent to the path. This is different than centripetal acceleration!

Rotational Kinematics § These rotational quantities we have just introduced are all vectors, so the have magnitude and DIRECTION. DO NOT FORGET TO USE THE CORRECT SIGN WHEN DOING CALCULATIONS! § Using the relationships between our linear and angular terms, we can take our linear kinematic equations and create a set of kinematics that can be used for a rotating object! Linear Kinematics Rotational Kinematics

Example A car engine is idling at 500 RPM. When the light turns green, the crankshaft rotation speeds up at a constant rate to 2500 RPM over and interval of 3. 0 s. How many revolutions does the crankshaft go through during this interval? 75 Revolutions

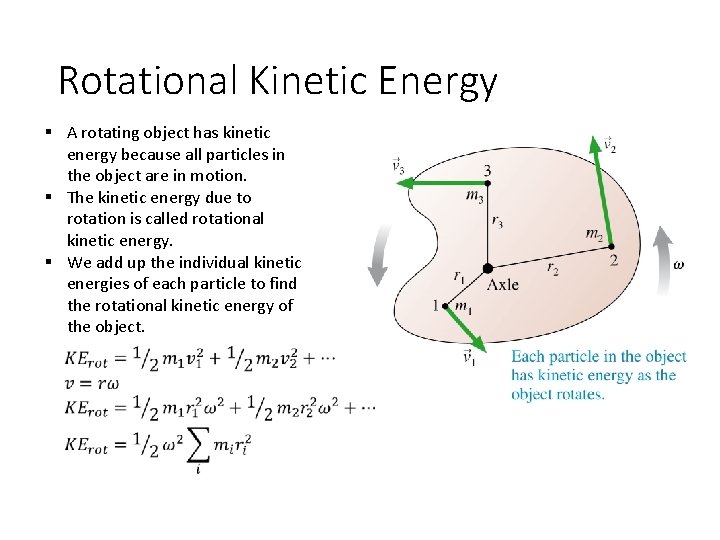
Rotational Kinetic Energy § A rotating object has kinetic energy because all particles in the object are in motion. § The kinetic energy due to rotation is called rotational kinetic energy. § We add up the individual kinetic energies of each particle to find the rotational kinetic energy of the object.

Rotational Kinetic Energy and Moment of Inertia § Looking at our formula for rotational kinetic energy, there is an interesting term: § We define this term as our moment of inertia, which is the rotational analog to inertia. § We use the letter I for moment of inertia, so we will substitute that into our formula for rotational kinetic energy. § This is not a new form of energy, merely the familiar kinetic energy of motion written in a new way.

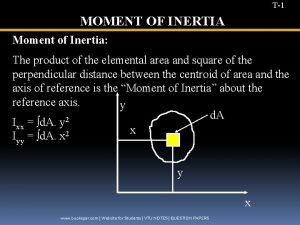
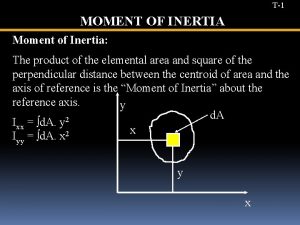
Moment of Inertia § Moment of Inertia represents an object’s resistance to change in rotational motion. This is a fancy way of saying it represents and object’s resistance to angular acceleration. § The units of moment of inertia are kg m 2. § The moment of inertia is the rotational equivalent of mass. § An object’s moment of inertia depends not only on the object’s mass but also on how the mass is distributed around the rotation axis. § If the object is a collection of point masses, the moment of inertia of the system is given by the formula:

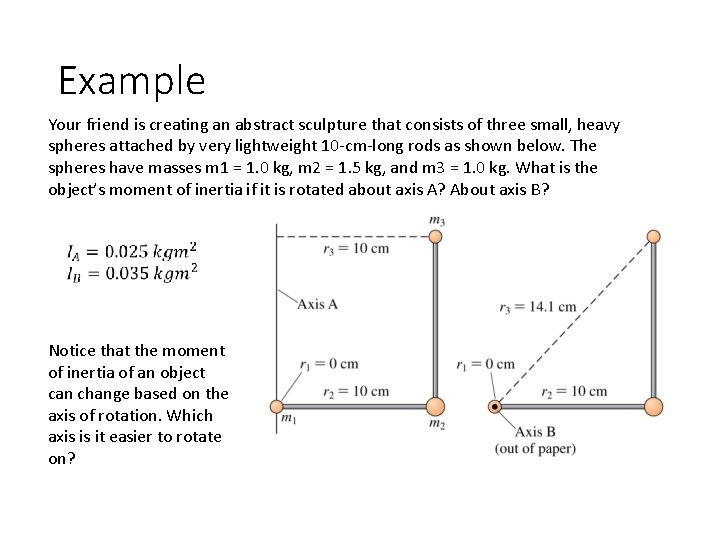
Example Your friend is creating an abstract sculpture that consists of three small, heavy spheres attached by very lightweight 10 -cm-long rods as shown below. The spheres have masses m 1 = 1. 0 kg, m 2 = 1. 5 kg, and m 3 = 1. 0 kg. What is the object’s moment of inertia if it is rotated about axis A? About axis B? Notice that the moment of inertia of an object can change based on the axis of rotation. Which axis is it easier to rotate on?

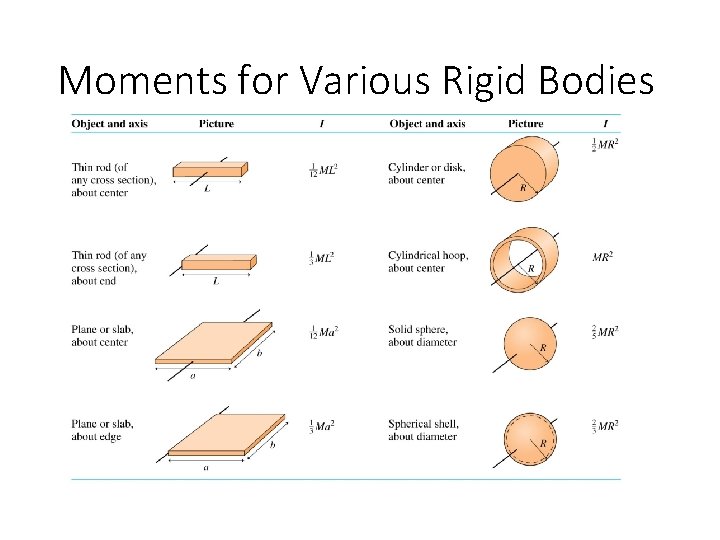
Moment of Inertia of a Rigid Body § Most of the time our rotating object will not be a collection of point masses, but rather a rigid body. To find the moment of inertia of rigid bodies, our formula for moment of inertia changes from a summation to an integral. Hooray for calculus! § Because this class is algebra based, you will not be asked to find moment of inertia this way. § We instead will use a table that has the formulas for moment of inertia for various rigid bodies. § You will notice that the formula changes based on the shape of the rigid body and the axis about which it is rotated.

Moments for Various Rigid Bodies

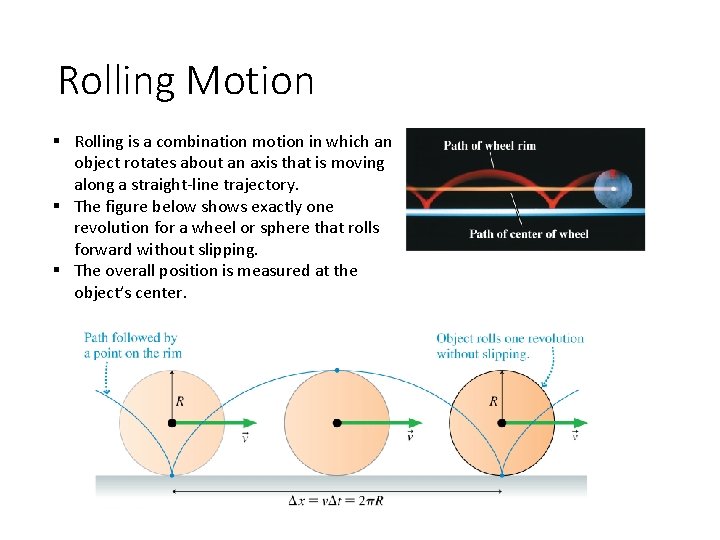
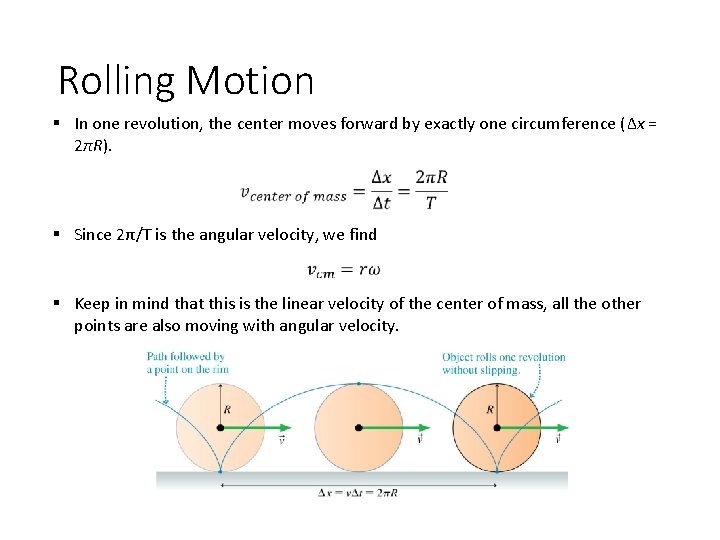
Rolling Motion § Rolling is a combination motion in which an object rotates about an axis that is moving along a straight-line trajectory. § The figure below shows exactly one revolution for a wheel or sphere that rolls forward without slipping. § The overall position is measured at the object’s center.

Rolling Motion § In one revolution, the center moves forward by exactly one circumference (Δx = 2πR). § Since 2π/T is the angular velocity, we find § Keep in mind that this is the linear velocity of the center of mass, all the other points are also moving with angular velocity.

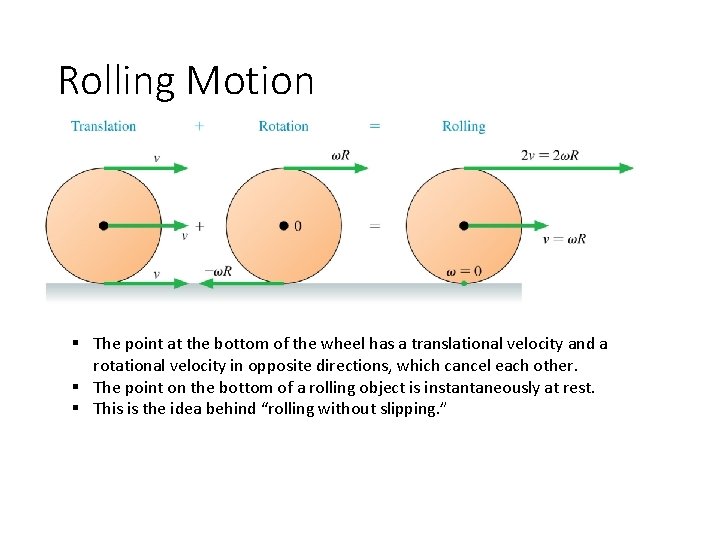
Rolling Motion § The point at the bottom of the wheel has a translational velocity and a rotational velocity in opposite directions, which cancel each other. § The point on the bottom of a rolling object is instantaneously at rest. § This is the idea behind “rolling without slipping. ”

Rolling Motion and Energy § To describe the kinetic energy of a rolling object, we must take into account the linear velocity and the rotational velocity of the object. § This means that the total kinetic energy of a rolling object can be calculated by adding the linear kinetic energy of the center of mass and the rotational kinetic energy about the center of mass. § When calculating total energy we will often use our linear-angular velocity relationship to make substitutions: § Doing this makes both types of kinetic energy easier to combine.

Example A ball rolls down a ramp of height 2 m (the ball starts from rest at the top of the ramp). The ball is solid, so its moment of inertia is given by the formula: Determine the velocity of the ball at the bottom of the ramp. Hint: Total mechanical energy is conserved.
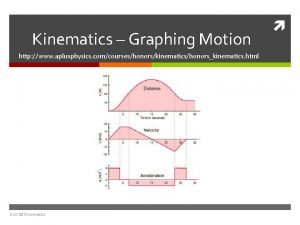
 Aplusphysics kinematics-horizontal kinematics
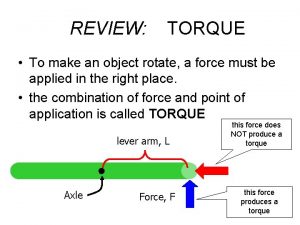
Aplusphysics kinematics-horizontal kinematics Torque free body diagram
Torque free body diagram Second condition of equilibrium
Second condition of equilibrium Equation for torque and angular velocity
Equation for torque and angular velocity Translational and rotational equilibrium
Translational and rotational equilibrium 4 linear motion equations
4 linear motion equations Kinematics equations
Kinematics equations Rotational kinematics
Rotational kinematics Rotational kinematics
Rotational kinematics Angular acceleration
Angular acceleration Parallel axis theorem ap physics c
Parallel axis theorem ap physics c How make your small big
How make your small big Youtube.com
Youtube.com Icm + md^2
Icm + md^2 Rotational inertia
Rotational inertia Moment of inertia units
Moment of inertia units A sanding disk with rotational inertia
A sanding disk with rotational inertia Moment of inertia of different sections
Moment of inertia of different sections Parallel axis theorem area moment of inertia
Parallel axis theorem area moment of inertia Define radius of gyration
Define radius of gyration Symbol for angular acceleration
Symbol for angular acceleration Horizontal centroidal axis
Horizontal centroidal axis Ix=bh^3/12
Ix=bh^3/12 Moments of inertia statics
Moments of inertia statics Radius of gyration
Radius of gyration