Moment of Inertia Area Moment of Inertia MET

Moment of Inertia Area Moment of Inertia MET 2214 Statics (MET 2214) Prof. Simin Nasseri

MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA, & MOMENTS OF INTERTIA BY INTEGRATION Objectives: You will be able to: a) Define the moments of inertia (Mo. I) for an area. b) Determine the Mo. I for an area by integration. Statics (MET 2214) Prof. Simin Nasseri

APPLICATIONS Many structural members like beams and columns have cross sectional shapes like I, H, C, etc. Some others are made of tubes rather than solid squares or rounds. Why do they usually not have solid rectangular, square, or circular cross sectional areas? What primary property of these members influences design decisions? How can we calculate this property? Statics (MET 2214) Prof. Simin Nasseri

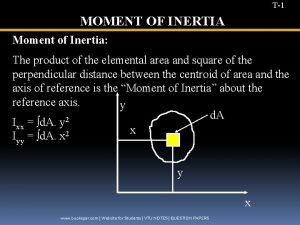
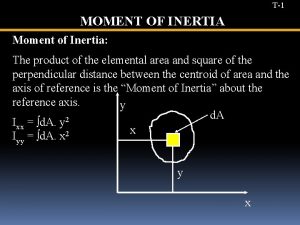
MOMENTS OF INERTIA FOR AREAS Consider a plate submerged in a liquid. The pressure of a liquid at a distance z below the surface is given by p = z, where is the specific weight of the liquid. The force on the area d. A at that point is d. F = p d. A. The moment about the x-axis due to this force is z(d. F). The total moment is A z d. F = A z 2 d. A = A( z 2 d. A). This sort of integral term also appears in solid mechanics when determining stresses and deflection. This integral term is referred to as the moment of inertia of the area of the plate about an axis. Statics (MET 2214) Prof. Simin Nasseri

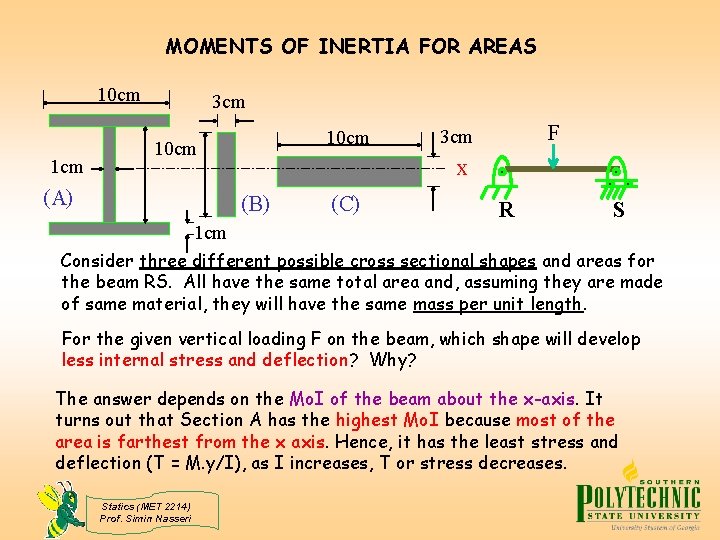
MOMENTS OF INERTIA FOR AREAS 10 cm 1 cm 3 cm 10 cm (A) x (B) 1 cm F 3 cm (C) R S Consider three different possible cross sectional shapes and areas for the beam RS. All have the same total area and, assuming they are made of same material, they will have the same mass per unit length. For the given vertical loading F on the beam, which shape will develop less internal stress and deflection? Why? The answer depends on the Mo. I of the beam about the x-axis. It turns out that Section A has the highest Mo. I because most of the area is farthest from the x axis. Hence, it has the least stress and deflection (T = M. y/I), as I increases, T or stress decreases. Statics (MET 2214) Prof. Simin Nasseri

MOMENTS OF INERTIA FOR AREAS For the differential area d. A, shown in the figure: d Ix = y 2 d. A , d Iy = x 2 d. A , and, d JO = r 2 d. A , where JO is the polar moment of inertia about the pole O or z axis. The moments of inertia for the entire area are obtained by integration. Ix = A y 2 d. A ; JO = A r 2 d. A = Iy = A x 2 d. A A ( x 2 + y 2 ) d. A = Ix + I y The Mo. I is also referred to as the second moment of an area and has units of length to the fourth power (m 4 or in 4). Statics (MET 2214) Prof. Simin Nasseri

RADIUS OF GYRATION OF AN AREA A y kx For a given area A and its Mo. I, Ix , imagine that the entire area is located at distance kx from the x axis. Then, Ix = kx 2 A or kx = ( Ix / A). x This kx is called the radius of gyration of the area about the x axis. Similarly; k. Y = ( Iy / A ) and k. O = ( JO / A ) The radius of gyration has units of length and gives an indication of the spread of the area from the axes. This characteristic is important when designing columns. Statics (MET 2214) Prof. Simin Nasseri

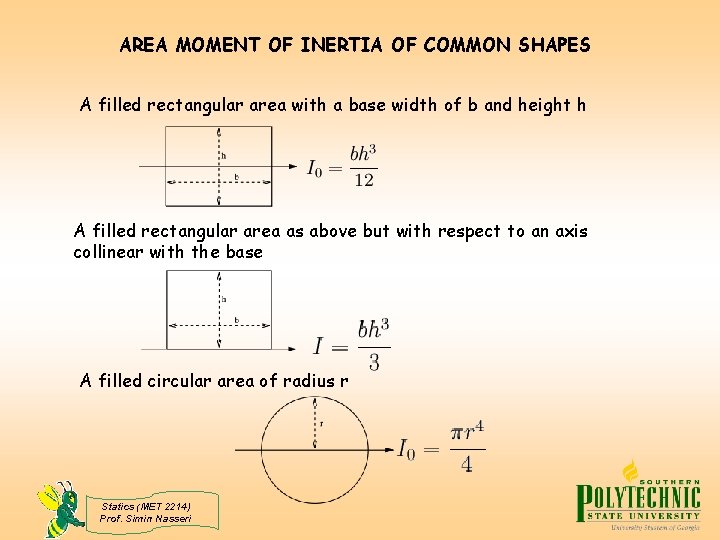
AREA MOMENT OF INERTIA OF COMMON SHAPES A filled rectangular area with a base width of b and height h A filled rectangular area as above but with respect to an axis collinear with the base A filled circular area of radius r Statics (MET 2214) Prof. Simin Nasseri

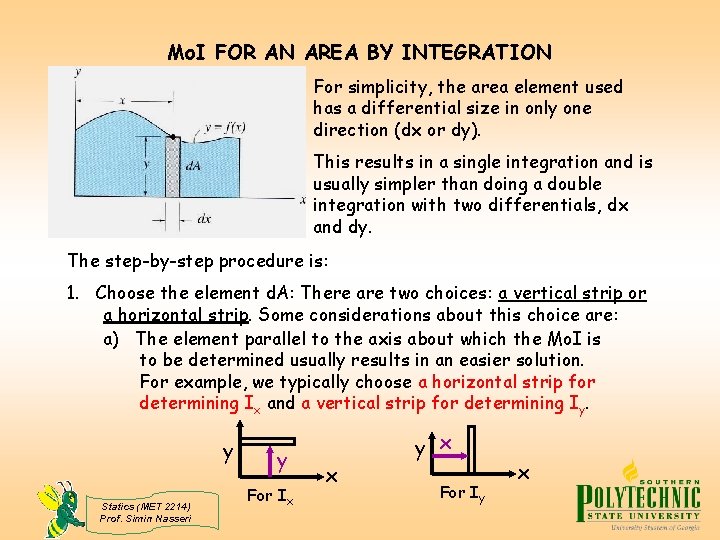
Mo. I FOR AN AREA BY INTEGRATION For simplicity, the area element used has a differential size in only one direction (dx or dy). This results in a single integration and is usually simpler than doing a double integration with two differentials, dx and dy. The step-by-step procedure is: 1. Choose the element d. A: There are two choices: a vertical strip or a horizontal strip. Some considerations about this choice are: a) The element parallel to the axis about which the Mo. I is to be determined usually results in an easier solution. For example, we typically choose a horizontal strip for determining Ix and a vertical strip for determining Iy. y Statics (MET 2214) Prof. Simin Nasseri y For Ix x y x For Iy x

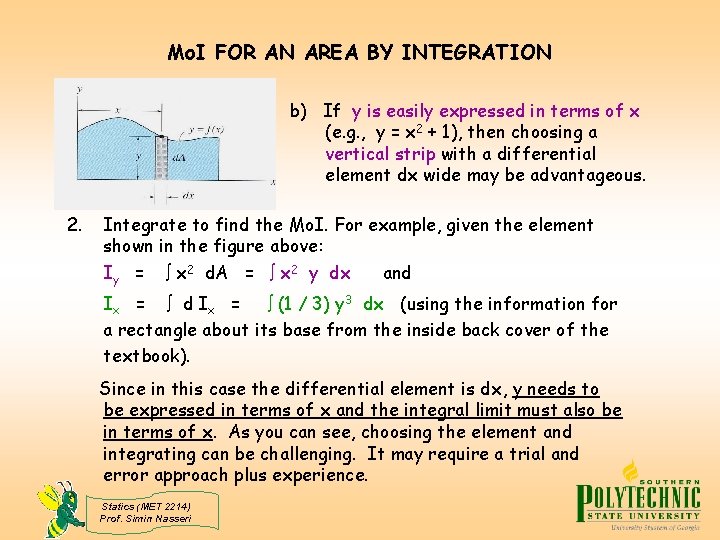
Mo. I FOR AN AREA BY INTEGRATION b) If y is easily expressed in terms of x (e. g. , y = x 2 + 1), then choosing a vertical strip with a differential element dx wide may be advantageous. 2. Integrate to find the Mo. I. For example, given the element shown in the figure above: Iy = x 2 d. A = x 2 y dx and Ix = (1 / 3) y 3 dx (using the information for a rectangle about its base from the inside back cover of the textbook). Since in this case the differential element is dx, y needs to be expressed in terms of x and the integral limit must also be in terms of x. As you can see, choosing the element and integrating can be challenging. It may require a trial and error approach plus experience. Statics (MET 2214) Prof. Simin Nasseri

READING QUIZ 1. The definition of the Moment of Inertia for an area involves an integral of the form A) x d. A. B) x 2 d. A. C) x 2 dm. D) m d. A. 2. Select the SI units for the Moment of Inertia for an area. A) m 3 B) m 4 C) kg·m 2 D) kg·m 3 Statics (MET 2214) Prof. Simin Nasseri

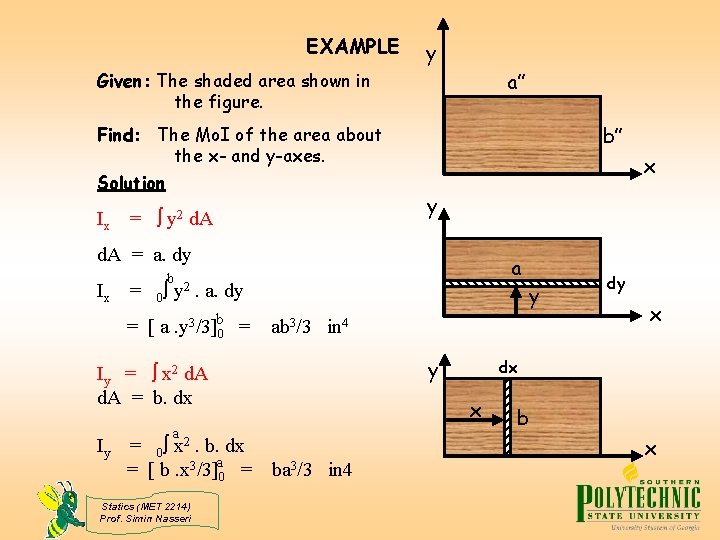
EXAMPLE y a” Given: The shaded area shown in the figure. Find: The Mo. I of the area about the x- and y-axes. Solution Ix = y 2 d. A b” x y d. A = a. dy Ix = a b 0 y 2. a. dy = [ a. y 3/3]b 0 = y ab 3/3 in 4 y Iy = x 2 d. A = b. dx Iy = 0 x 2. b. dx = [ b. x 3/3]a 0 = Statics (MET 2214) Prof. Simin Nasseri ba 3/3 in 4 x dx x a dy b x

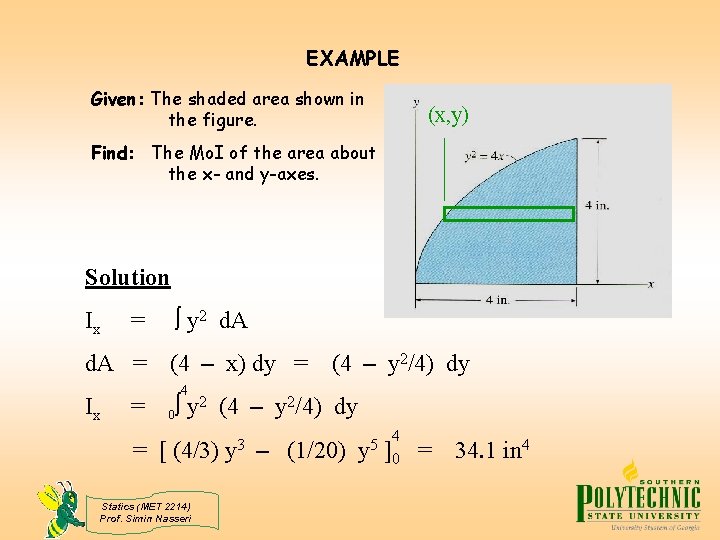
EXAMPLE Given: The shaded area shown in the figure. (x, y) Find: The Mo. I of the area about the x- and y-axes. Solution Ix d. A = Ix y 2 d. A = = (4 – x) dy = (4 – y 2/4) dy 4 0 y 2 (4 – y 2/4) dy = [ (4/3) Statics (MET 2214) Prof. Simin Nasseri y 3 – (1/20) y 5 4 ]0 = 34. 1 in 4

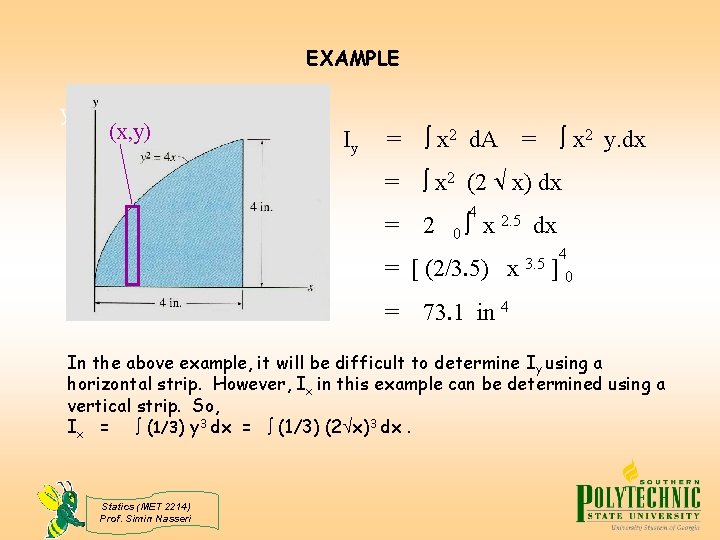
EXAMPLE y (x, y) Iy = x 2 d. A = x 2 (2 x) dx = 2 4 0 x 2. 5 dx = [ (2/3. 5) x = x 2 y. dx = 3. 5 4 ]0 73. 1 in 4 In the above example, it will be difficult to determine Iy using a horizontal strip. However, Ix in this example can be determined using a vertical strip. So, Ix = (1/3) y 3 dx = (1/3) (2 x)3 dx. Statics (MET 2214) Prof. Simin Nasseri

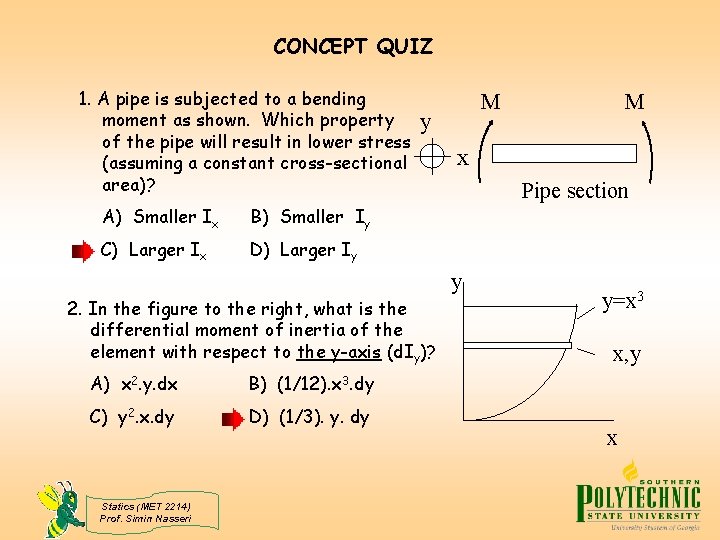
CONCEPT QUIZ 1. A pipe is subjected to a bending moment as shown. Which property of the pipe will result in lower stress (assuming a constant cross-sectional area)? A) Smaller Ix B) Smaller Iy C) Larger Ix D) Larger Iy M y x Pipe section y 2. In the figure to the right, what is the differential moment of inertia of the element with respect to the y-axis (d. Iy)? A) x 2. y. dx B) (1/12). x 3. dy C) y 2. x. dy D) (1/3). y. dy Statics (MET 2214) Prof. Simin Nasseri M y=x 3 x, y x

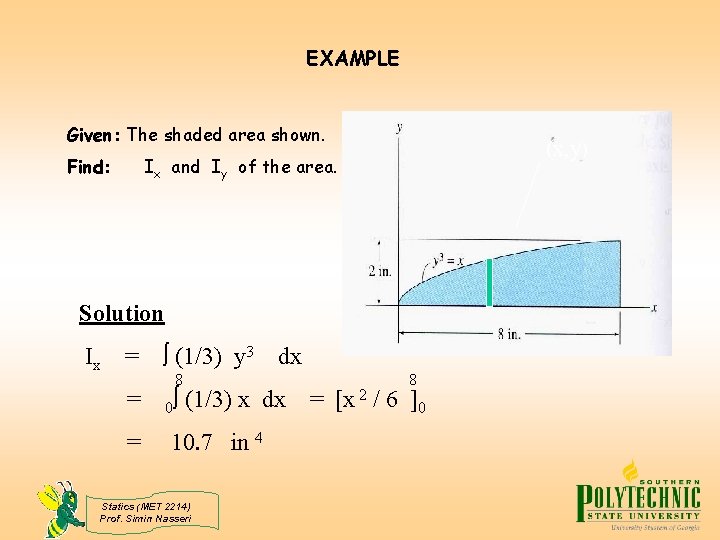
EXAMPLE Given: The shaded area shown. Find: (x, y) Ix and Iy of the area. Solution Ix = = = (1/3) y 3 dx 8 0 (1/3) x dx 10. 7 in 4 Statics (MET 2214) Prof. Simin Nasseri = [x 2 8 / 6 ]0

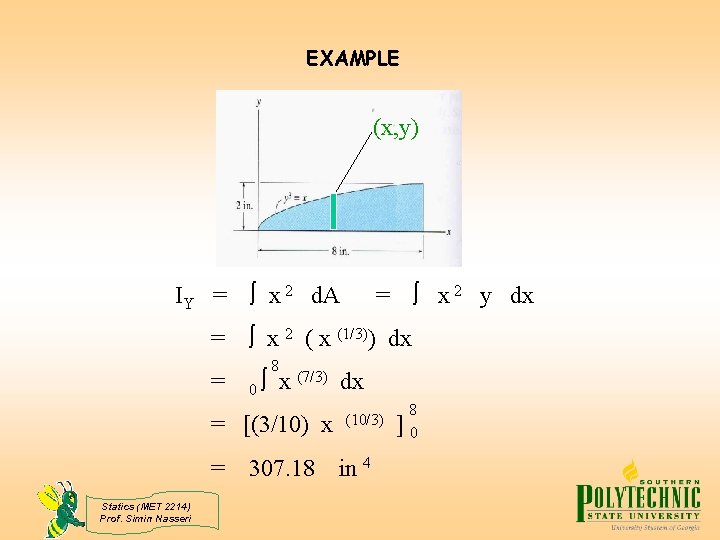
EXAMPLE (x, y) IY = = = x 2 d. A x 2 ( x (1/3)) dx 0 8 x (7/3) dx = [(3/10) x = Statics (MET 2214) Prof. Simin Nasseri x 2 y dx = 307. 18 (10/3) in 4 ] 8 0

ATTENTION QUIZ 1. When determining the Mo. I of the element in the figure, d. Iy equals A) x 2 dy C) (1/3) y B) x dx 3 2 (x, y) dx D) x 2. 5 dx y 2 = x 2. Similarly, d. Ix equals A) (1/3) x 1. 5 C) (1/12) x Statics (MET 2214) Prof. Simin Nasseri 3 dx B) y dy D) (1/3) x 2 d. A 3 dx