DEFINITION OF MOMENTS OF INERTIA FOR AREAS RADIUS

DEFINITION OF MOMENTS OF INERTIA FOR AREAS, RADIUS OF GYRATION OF AN AREA Today’s Objectives: Students will be able to: a) Define the moments of inertia (Mo. I) for an area. b) Determine the Mo. I for an area by integration.

APPLICATIONS Many structural members like beams and columns have cross sectional shapes like an I, H, C, etc. Why do they usually not have solid rectangular, square, or circular cross sectional areas? What primary property of these members influences design decisions?

DEFINITION OF MOMENTS OF INERTIA FOR AREAS (Section 10. 1) Consider a plate submerged in a liquid. The pressure of a liquid at a distance y below the surface is given by p = y, where is the specific weight (Weight/Volume) of the liquid. The force on the area d. A at that point is d. F = p d. A. The moment about the x-axis due to this force is y (d. F). The total moment is A y d. F = A y 2 d. A = A( y 2 d. A). This sort of integral term also appears in solid mechanics when determining stresses and deflection. This integral term is referred to as the moment of inertia of the area of the plate about an axis.

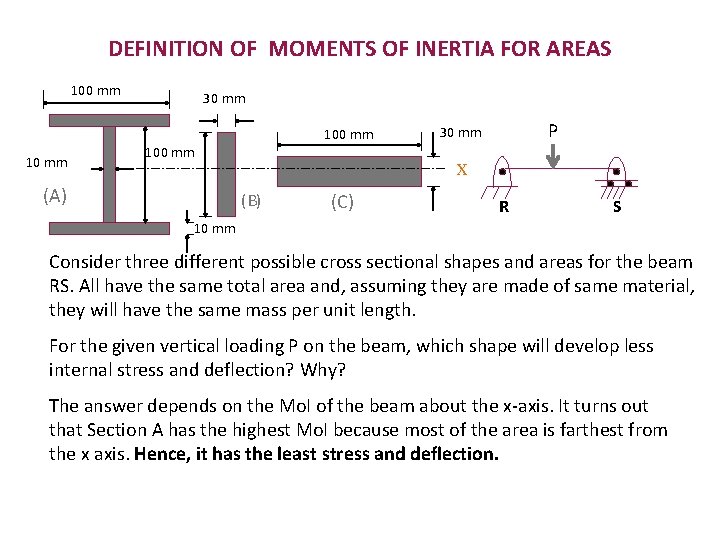
DEFINITION OF MOMENTS OF INERTIA FOR AREAS 100 mm 10 mm 30 mm 100 mm (A) P 30 mm x (B) (C) R S 10 mm Consider three different possible cross sectional shapes and areas for the beam RS. All have the same total area and, assuming they are made of same material, they will have the same mass per unit length. For the given vertical loading P on the beam, which shape will develop less internal stress and deflection? Why? The answer depends on the Mo. I of the beam about the x-axis. It turns out that Section A has the highest Mo. I because most of the area is farthest from the x axis. Hence, it has the least stress and deflection.

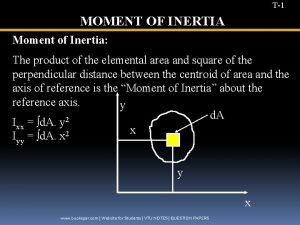
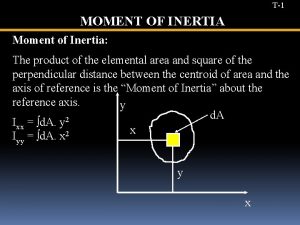
DEFINITION OF MOMENTS OF INERTIA FOR AREAS For the differential area d. A, shown in the figure: d Ix = y 2 d. A , d Iy = x 2 d. A , and d JO = r 2 d. A , where JO is the polar moment of inertia about the pole O or z axis. The moments of inertia for the entire area are obtained by integration. Ix = A y 2 d. A ; Iy = A x 2 d. A JO = A r 2 d. A = A ( x 2 + y 2 ) d. A = Ix + I y The Mo. I is also referred to as the second moment of an area and has units of length to the fourth power (m 4 or in 4).

Mo. I FOR AN AREA BY INTEGRATION For simplicity, the area element used has a differential size in only one direction (dx or dy). This results in a single integration and is usually simpler than doing a double integration with two differentials, i. e. , dx·dy. The step-by-step procedure is: 1. Choose the element d. A: There are two choices: a vertical strip or a horizontal strip. Some considerations about this choice are: a) The element parallel to the axis about which the Mo. I is to be determined usually results in an easier solution. For example, we typically choose a horizontal strip for determining Ix and a vertical strip for determining Iy.

Mo. I FOR AN AREA BY INTEGRATION b) If y is easily expressed in terms of x (e. g. , y = x 2 + 1), then choosing a vertical strip with a differential element dx wide may be advantageous. 2. Integrate to find the Mo. I. For example, given the element shown in the figure above: Iy = x 2 d. A = x 2 y dx and Ix = (1 / 3) y 3 dx (using the parallel axis theorem as per Example 10. 2 of the textbook). Since the differential element is dx, y needs to be expressed in terms of x and the integral limit must also be in terms of x. As you can see, choosing the element and integrating can be challenging. It may require a trial and error approach, plus experience.

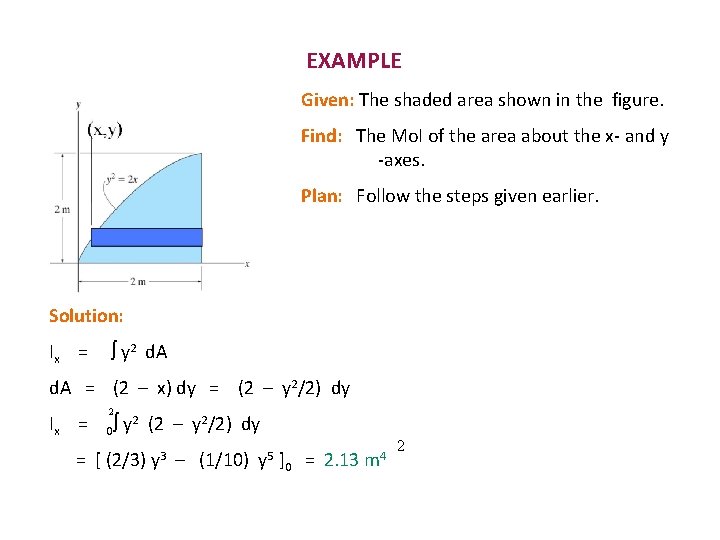
EXAMPLE Given: The shaded area shown in the figure. Find: The Mo. I of the area about the x- and y -axes. Plan: Follow the steps given earlier. Solution: Ix = y 2 d. A = (2 – x) dy = (2 – y 2/2) dy Ix = 2 0 y 2 (2 – y 2/2) dy = [ (2/3) y 3 – (1/10) y 5 ]0 = 2. 13 m 4 2

EXAMPLE (continued) Iy = x 2 d. A = x 2 y dx = x 2 ( 2 x) dx 2 = √ 2 0 x 2. 5 dx = [ (√ 2/3. 5) x 3. 5 ]0 2 = 4. 57 m 4 In this example, it would be difficult to determine Iy using a horizontal strip. However, Ix in this example can be determined using a vertical strip. Using a vertical strip, Ix = (1/3) y 3 dx = (1/3) ( 2 x)3 dx.

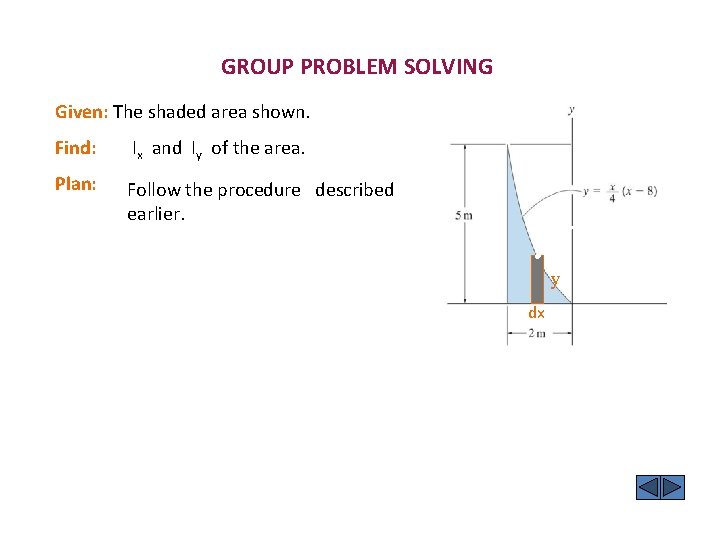
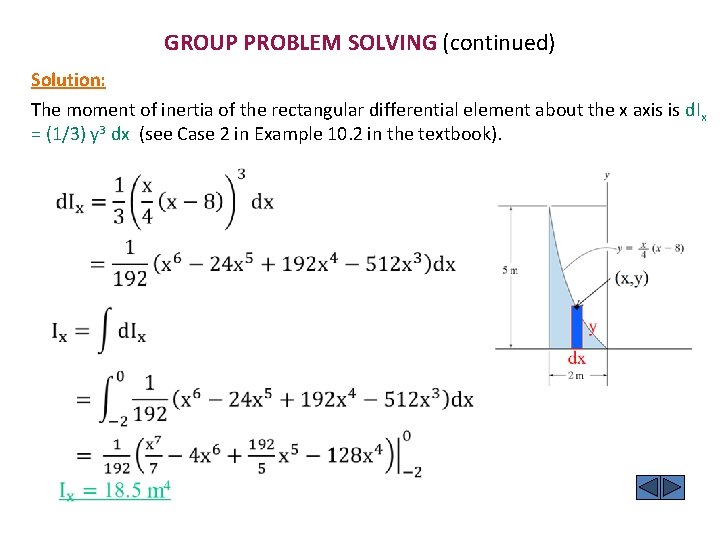
GROUP PROBLEM SOLVING Given: The shaded area shown. Find: Ix and Iy of the area. Plan: Follow the procedure described earlier. (x, y) y dx

GROUP PROBLEM SOLVING (continued) Solution: The moment of inertia of the rectangular differential element about the x axis is d. Ix = (1/3) y 3 dx (see Case 2 in Example 10. 2 in the textbook).

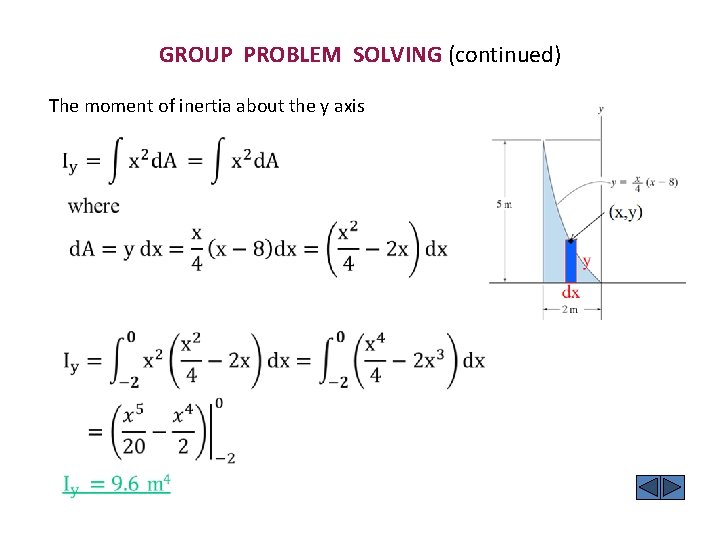
GROUP PROBLEM SOLVING (continued) The moment of inertia about the y axis

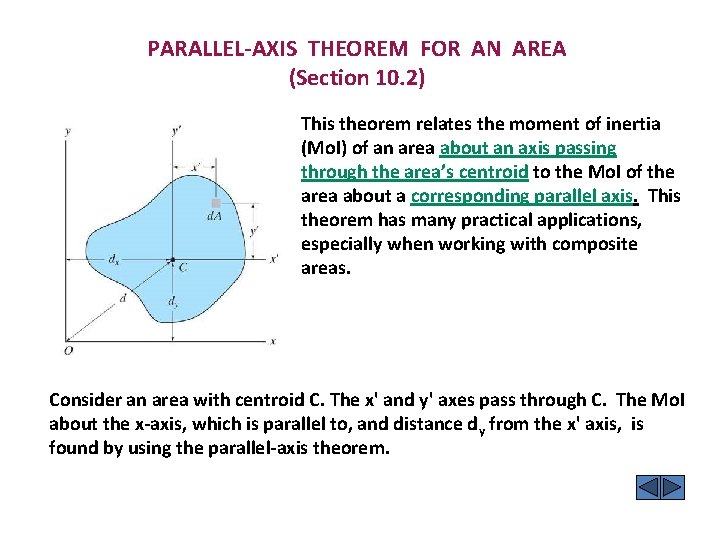
PARALLEL-AXIS THEOREM FOR AN AREA (Section 10. 2) This theorem relates the moment of inertia (Mo. I) of an area about an axis passing through the area’s centroid to the Mo. I of the area about a corresponding parallel axis. This theorem has many practical applications, especially when working with composite areas. Consider an area with centroid C. The x' and y' axes pass through C. The Mo. I about the x-axis, which is parallel to, and distance dy from the x' axis, is found by using the parallel-axis theorem.

PARALLEL-AXIS THEOREM (continued) IX = A y 2 d. A = A (y' + dy)2 d. A = A y' 2 d. A + 2 dy A y'd. A + dy 2 A d. A Using the definition of the centroid: y' = ( A y' d. A) / ( A d. A). Now since C is at the origin of the x' – y' axes, y' = 0 , and hence A y' d. A = 0. Thus IX = IX' + A d y 2 Similarly, IY = IY' + A d. X 2 and JO = J C + A d 2

MOMENT OF INERTIA FOR A COMPOSITE AREA (Section 10. 4) A composite area is made by adding or subtracting a series of “simple” shaped areas like rectangles, triangles, and circles. For example, the area on the left can be made from a rectangle plus a triangle, minus the interior rectangle. The Mo. I about their centroidal axes of these “simpler” shaped areas are found in most engineering handbooks. Using these data and the parallel-axis theorem, the Mo. I for a composite area can easily be calculated.

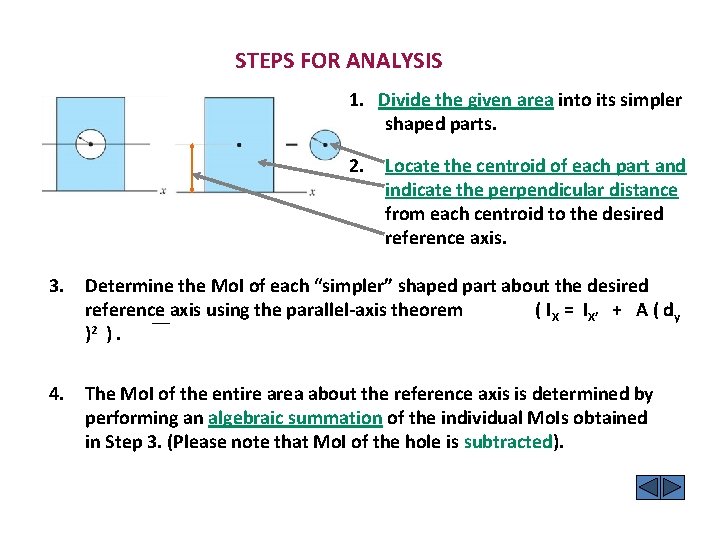
STEPS FOR ANALYSIS 1. Divide the given area into its simpler shaped parts. 2. Locate the centroid of each part and indicate the perpendicular distance from each centroid to the desired reference axis. 3. Determine the Mo. I of each “simpler” shaped part about the desired reference axis using the parallel-axis theorem ( IX = IX’ + A ( dy )2 ). 4. The Mo. I of the entire area about the reference axis is determined by performing an algebraic summation of the individual Mo. Is obtained in Step 3. (Please note that Mo. I of the hole is subtracted).

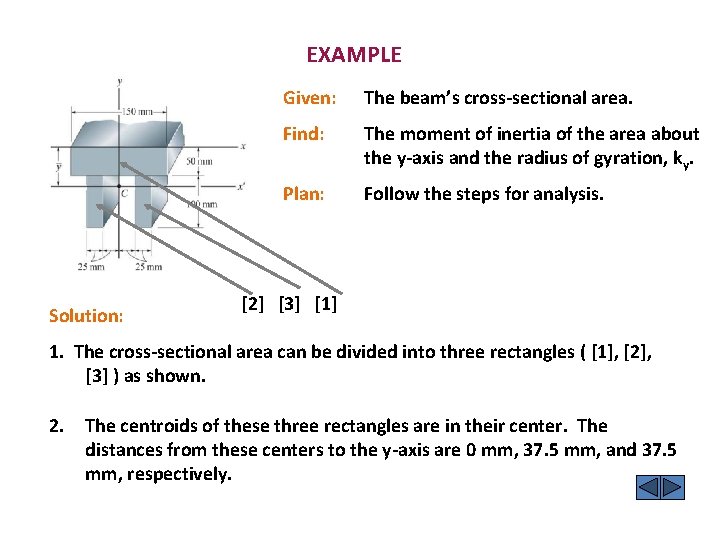
EXAMPLE Solution: Given: The beam’s cross-sectional area. Find: The moment of inertia of the area about the y-axis and the radius of gyration, ky. Plan: Follow the steps for analysis. [2] [3] [1] 1. The cross-sectional area can be divided into three rectangles ( [1], [2], [3] ) as shown. 2. The centroids of these three rectangles are in their center. The distances from these centers to the y-axis are 0 mm, 37. 5 mm, and 37. 5 mm, respectively.

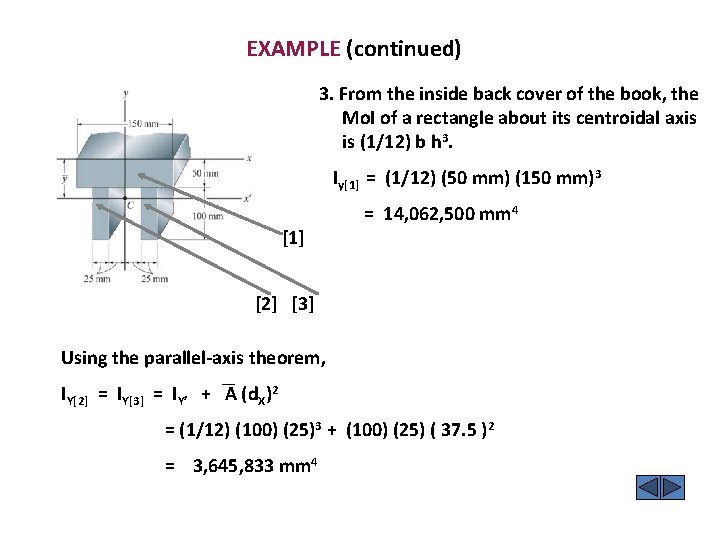
EXAMPLE (continued) 3. From the inside back cover of the book, the Mo. I of a rectangle about its centroidal axis is (1/12) b h 3. Iy[1] = (1/12) (50 mm) (150 mm)3 [1] = 14, 062, 500 mm 4 [2] [3] Using the parallel-axis theorem, IY[2] = IY[3] = IY’ + A (d. X)2 = (1/12) (100) (25)3 + (100) (25) ( 37. 5 )2 = 3, 645, 833 mm 4

EXAMPLE (continued) Summing these three Mo. Is: 4. Iy = Iy 1 + Iy 2 + Iy 3 Iy = 21, 354, 166 mm 4 Now, finding the radius of gyration: ky = ( Iy / A) A = 150 (50) + 100 (25) = 12500 mm 2 ky = (21, 354, 166) / (12500) = 41. 3 mm

MASS MOMENT OF INERTIA Obj: 1. Define the mass moments of inertia (MMI). b) Determine the MMI by integration.

APPLICATIONS (continued) If a torque M is applied to a fan blade initially at rest, its angular speed (rotation) begins to increase. Which property (which we will call P) of the fan blade do you think effects the angular acceleration ( ) the most? How can we determine a value for this property? What is the relationship between M, P, and ?

MASS MOMENT OF INERTIA Consider a rigid body with a center of mass at G. It is free to rotate about the z axis, which passes through G. Now, if we apply a torque T about the z axis to the body, the body begins to rotate with an angular acceleration . T and are related by the equation T = I . In this equation, I is the mass moment of inertia (MMI) about the z axis. The MMI of a body is a property that measures the resistance of the body to angular acceleration. This is similar to the role of mass in the equation F = m a. The MMI is often used when analyzing rotational motion (done in dynamics).

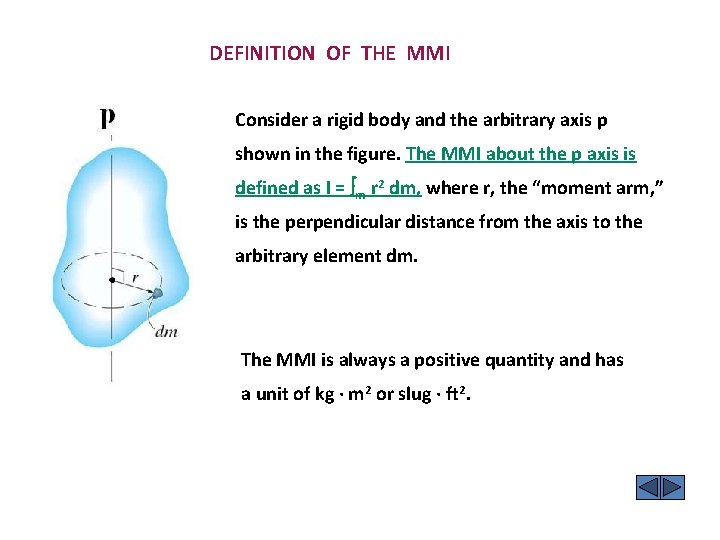
DEFINITION OF THE MMI Consider a rigid body and the arbitrary axis p shown in the figure. The MMI about the p axis is defined as I = m r 2 dm, where r, the “moment arm, ” is the perpendicular distance from the axis to the arbitrary element dm. The MMI is always a positive quantity and has a unit of kg · m 2 or slug · ft 2.

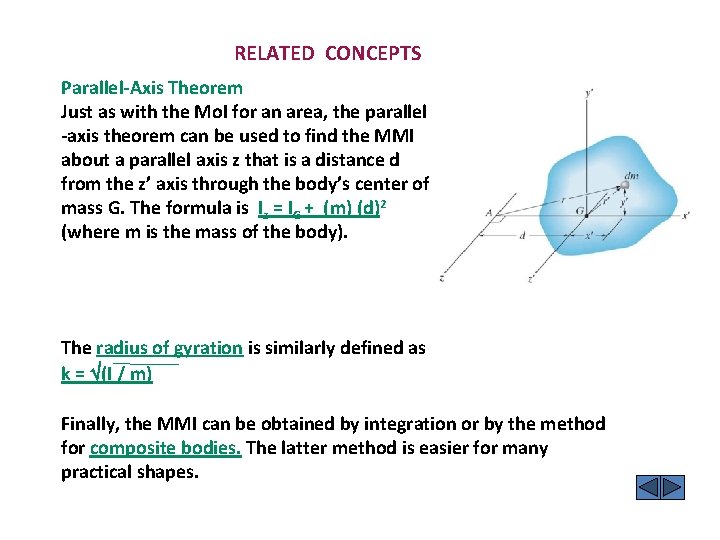
RELATED CONCEPTS Parallel-Axis Theorem Just as with the Mo. I for an area, the parallel -axis theorem can be used to find the MMI about a parallel axis z that is a distance d from the z’ axis through the body’s center of mass G. The formula is Iz = IG + (m) (d)2 (where m is the mass of the body). m The radius of gyration is similarly defined as k = (I / m) Finally, the MMI can be obtained by integration or by the method for composite bodies. The latter method is easier for many practical shapes.

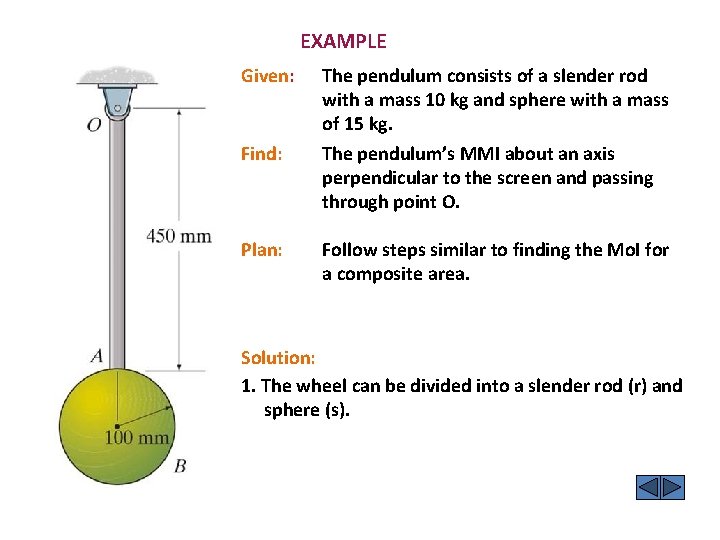
EXAMPLE Given: Find: Plan: The pendulum consists of a slender rod with a mass 10 kg and sphere with a mass of 15 kg. The pendulum’s MMI about an axis perpendicular to the screen and passing through point O. Follow steps similar to finding the Mo. I for a composite area. Solution: 1. The wheel can be divided into a slender rod (r) and sphere (s).

EXAMPLE (continued) 2. The center of mass for rod is at point Gr, 0. 225 m from Point O. The center of mass for sphere is at Gs, 0. 55 m from point O. Gr Gs O 3. The MMI data for a slender rod and sphere are given on the inside back cover of the textbook. Using those data and the parallel-axis theorem, calculate the following. IO = IG + (m) (d) 2 IOr = (1/12) (10)(0. 45)2 +10 (0. 225)2 = 0. 675 kg·m 2 IOs = (2/5) (15) (0. 1)2 + 15 (0. 55)2 = 4. 598 kg·m 2 4. Now add the three MMIs about point O. IO = IOr + IOs = 5. 27 kg·m 2

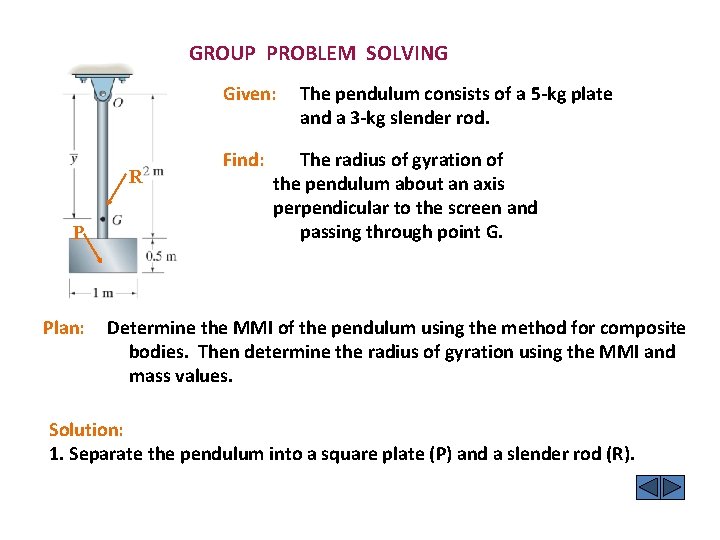
GROUP PROBLEM SOLVING Given: R P Plan: Find: The pendulum consists of a 5 -kg plate and a 3 -kg slender rod. The radius of gyration of the pendulum about an axis perpendicular to the screen and passing through point G. Determine the MMI of the pendulum using the method for composite bodies. Then determine the radius of gyration using the MMI and mass values. Solution: 1. Separate the pendulum into a square plate (P) and a slender rod (R).

GROUP PROBLEM SOLVING (continued) 2. The center of mass of the plate and rod are 2. 25 m and 1 m from point O, respectively. y = ( y m) / ( m ) = {(1) 3 + (2. 25) 5} / (3+5) = 1. 781 m 3. Using the MMI data on plates and slender rods and the parallel-axis theorem, IP = (1/12) 5 (0. 52 + 12) + 5 (2. 25 1. 781)2 = 1. 621 kg·m 2 IR = (1/12) 3 (2)2 + 3 (1. 781 1)2 = 2. 830 kg·m 2

GROUP PROBLEM SOLVING (continued) 4. IO = IP + IR = 1. 621 + 2. 830 = 4. 45 kg·m 2 5. Total mass (m) equals 8 kg Radius of gyration k = IO / m = 4. 45 / 8 = 0. 746 m

Do EXAMPLE 10. 13 Find the pendulum’s mass moment of inertia about an axis passing through: 1. The pin at O. 2. The mass center G of the pendulum.