Rotational Kinematics AP Physics C Rotational Kinematics l






















- Slides: 26

Rotational Kinematics AP Physics C

Rotational Kinematics l Just like basic kinematics, rotational kinematics follows similar principles and equations. l l Throughout today’s discussion you will see the connection between linear kinematics and rotational kinematics. You will also be able to solve problems involving rotational kinematics.

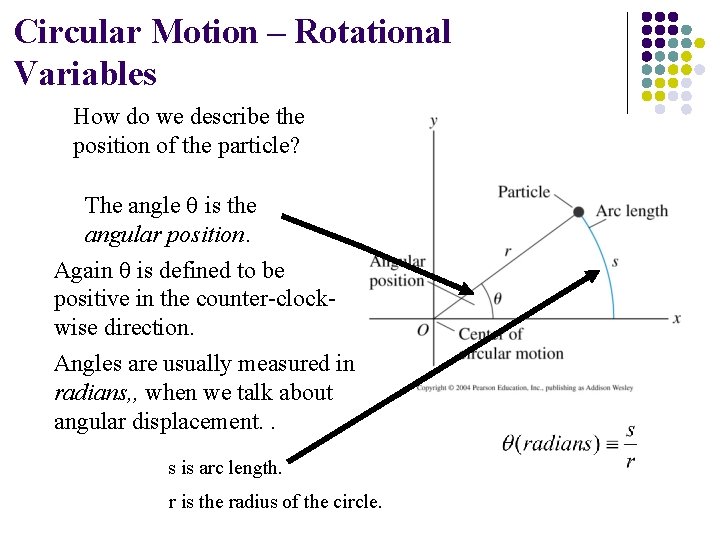
Circular Motion – Rotational Variables How do we describe the position of the particle? The angle q is the angular position. Again q is defined to be positive in the counter-clockwise direction. Angles are usually measured in radians, , when we talk about angular displacement. . s is arc length. r is the radius of the circle.

Angular Position: θ

Angular Position: θ Degrees and revolutions: 1 rev = 2π = 360˚

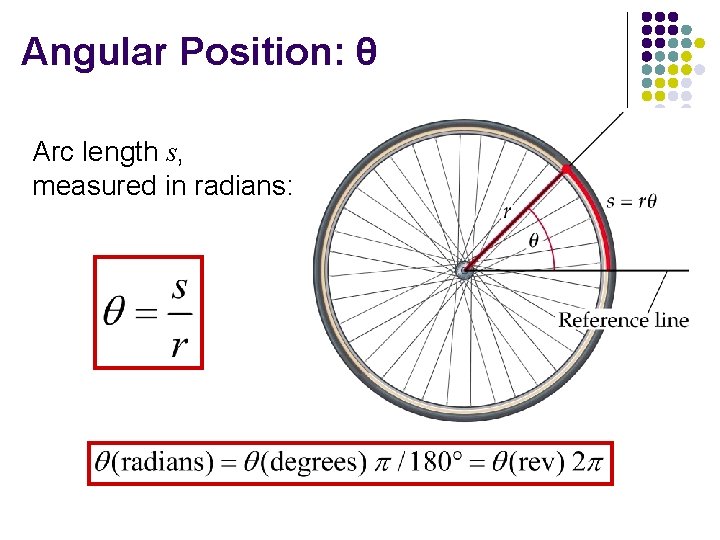
Angular Position: θ Arc length s, measured in radians:

Angular Velocity: ω Angular velocity The angular displacement is Average angular velocity Instantaneous angular velocity Relationship between vt and w Positive angular velocity is counter -clockwise.

Example Problem A particle is moving in a circle of radius 3 m according to the relation = t 3 + 4 t 2 + 6 t, where is measured in radians and t in seconds. The speed of the particle at t = 4 seconds is

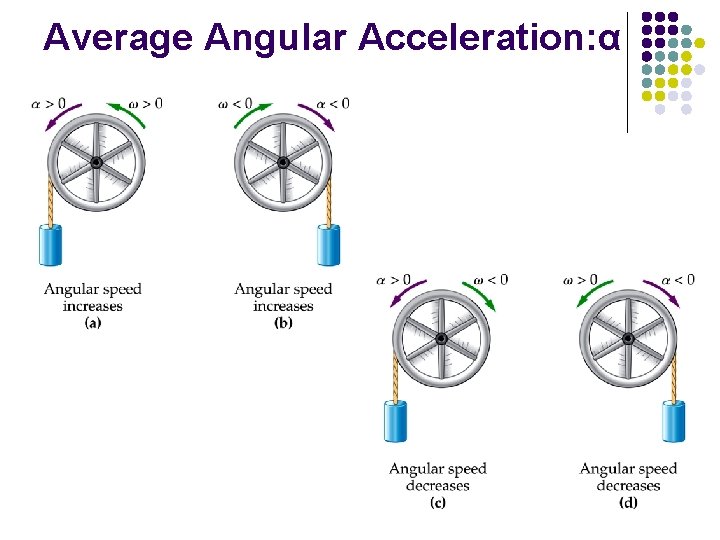
Average Angular Acceleration: α l The average angular acceleration, a, of an object is defined as the ratio of the change in the angular speed to the time it takes for the object to undergo the change: t = t i : wi t = t f : wf

Average Angular Acceleration: α

Instantaneous Angular Acceleration: α l The instantaneous angular acceleration is defined as the limit of the average angular acceleration as the time goes to 0 l SI Units of angular acceleration: rad/s² Positive angular acceleration l l if an object rotating ccw is speeding up if an object rotating cw is slowing down Negative angular acceleration l l if an object rotating ccw is slowing down if an object rotating cw is speeding up

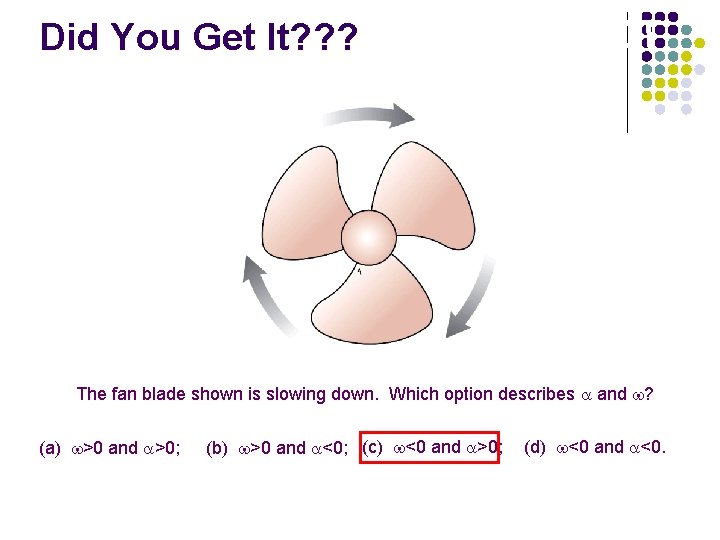
Angular & Acceleration ACT Did You. Velocity Get It? ? ? The fan blade shown is slowing down. Which option describes a and w? (a) w>0 and a>0; (b) w>0 and a<0; (c) w<0 and a>0; (d) w<0 and a<0.

Acceleration in Nonuniform Circular Motion Average Acceleration: α l l The particle in the figure is moving along a circle and is speeding up. The centripetal acceleration is ar vt 2/r, where vt is the tangential speed. There is also a tangential acceleration at, which is always tangent to the circle. The magnitude of the total acceleration is Slide 4 -115

Speed and Acceleration Note l l l All points on the rigid object will have the same angular speed, but not the same tangential speed All points on the rigid object will have the same angular acceleration, but not the same tangential acceleration The tangential quantities depend on r, and r is not the same for all points on the object

. 12 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s angular velocity is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -95

Quick. Check 4. 12 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s angular velocity is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -96

Quick. Check 4. 13 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s speed is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -97

Quick. Check 4. 13 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s speed is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -98

Quick. Check 4. 14 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s acceleration is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -99

Quick. Check 4. 14 Did You Get It? ? ? Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s acceleration is ______ that of Rasheed. A. half B. the same as C. twice D. four times E. We can’t say without knowing their radii. Slide 4 -100

Rotational Kinematics l A number of parallels exist between the equations for rotational motion and those for linear motion. l Under constant angular acceleration, we can describe the motion of the rigid object using a set of kinematic equations l These are similar to the kinematic equations for linear motion l The rotational equations have the same mathematical form as the linear equations

Comparison Between Rotational and Linear Equations

A Rotating Wheel Example l A wheel rotates with a constant angular acceleration of 3. 5 rad/s 2. If the angular speed of the wheel is 2. 0 rad/s at t = 0 (a) through what angle does the wheel rotate between t = 0 and t = 2. 0 s? Given your answer in radians and in revolutions. (b) What is the angular speed of the wheel at t = 2. 0 s?

A 3 cm diameter crankshaft rotates at 2500 rpm comes to a halt in 1. 5 s. a) b) c) What is the angular acceleration? What is the tangential acceleration? How many revolutions does it turn through before it stops.

A wheel rotates with a constant angular acceleration of 3. 50 rad/s 2. If the angular speed of the wheel is 2. 00 rad/s at t = 0 s. a. Through what angular displacement does the wheel rotate in 2 s? b. How many revolutions does it make? c. What is the angular speed of the wheel at t = 2. 00 s?

Exit Ticket On a separate sheet of paper, answer the following questions. Be sure to show all work and include units. 1) 2) A potter’s wheel moves uniformly from rest to an angular speed of 1. 00 rev/s in 30. 0 s. Find its average angular acceleration in radians per second squared. During a the time interval, the angular position of a door is described by θ = 5. 00 + 10. 0 t + 2. 00 t 2. Determine the angular position, angular speed , and angular acceleration of the door at t = 0 and 3 seconds.
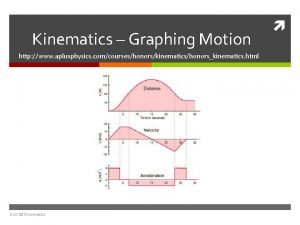
 Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Angular acceleration
Angular acceleration Rotational kinematics
Rotational kinematics Rotational kinematics
Rotational kinematics Constant angular acceleration
Constant angular acceleration Rotational kinematics
Rotational kinematics Torque right hand rule
Torque right hand rule Rotational equilibrium and rotational dynamics
Rotational equilibrium and rotational dynamics A level physics kinematics
A level physics kinematics Ib physics data booklet
Ib physics data booklet Kinematics
Kinematics A level physics kinematics
A level physics kinematics Ap physics c rotational motion
Ap physics c rotational motion Torque of gravity
Torque of gravity Ap physics unit 7
Ap physics unit 7 Rolling physics
Rolling physics University physics with modern physics fifteenth edition
University physics with modern physics fifteenth edition Linkedin
Linkedin Modern physics vs classical physics
Modern physics vs classical physics Forward kinematics
Forward kinematics Forward kinematics
Forward kinematics Define variable acceleration
Define variable acceleration Tempus
Tempus Kinematics
Kinematics Rrt
Rrt Body kinematics
Body kinematics Rectilinear kinematics continuous motion
Rectilinear kinematics continuous motion