T1 MOMENT OF INERTIA Moment of Inertia The

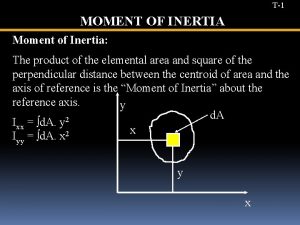
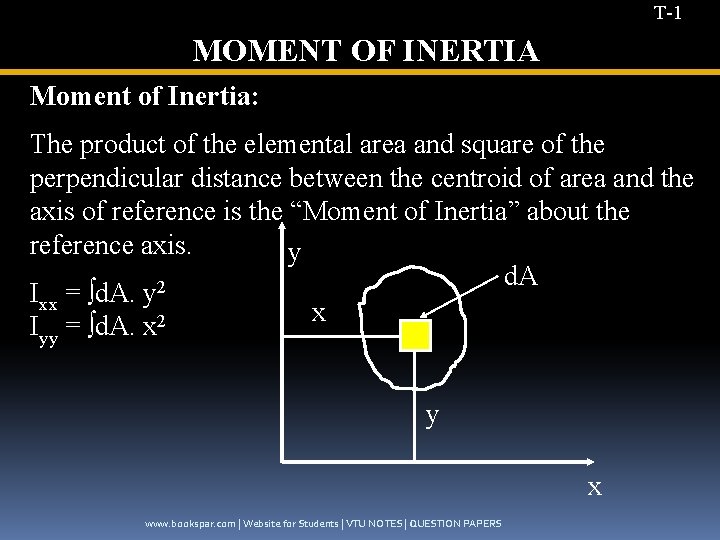
T-1 MOMENT OF INERTIA Moment of Inertia: The product of the elemental area and square of the perpendicular distance between the centroid of area and the axis of reference is the “Moment of Inertia” about the reference axis. y d. A 2 Ixx = ∫d. A. y x Iyy = ∫d. A. x 2 y x www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

T-2 It is also called second moment of area because first moment of elemental area is d. A. y and d. A. x; and if it is again multiplied by the distance, we get second moment of elemental area as (d. A. y)y and (d. A. x)x. www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

T-3 Polar moment of Inertia (Perpendicular Axes theorem) The moment of inertia of an area about an axis perpendicular to the plane of the area is called “Polar Moment of Inertia” and it is denoted by symbol Izz or J or Ip. The moment of inertia of an area in xy plane w. r. to z. axis is Izz = Ip = J = ∫r 2 d. A = ∫(x 2 + y 2) d. A = ∫x 2 d. A + ∫y 2 d. A = Ixx +Iyy Y x r y O z www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS x

T-4 PERPENDICULAR AXIS THEOREM Hence polar M. I. for an area w. r. t. an axis perpendicular to its plane of area is equal to the sum of the M. I. about any two mutually perpendicular axes in its plane, passing through the point of intersection of the polar axis and the area. www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

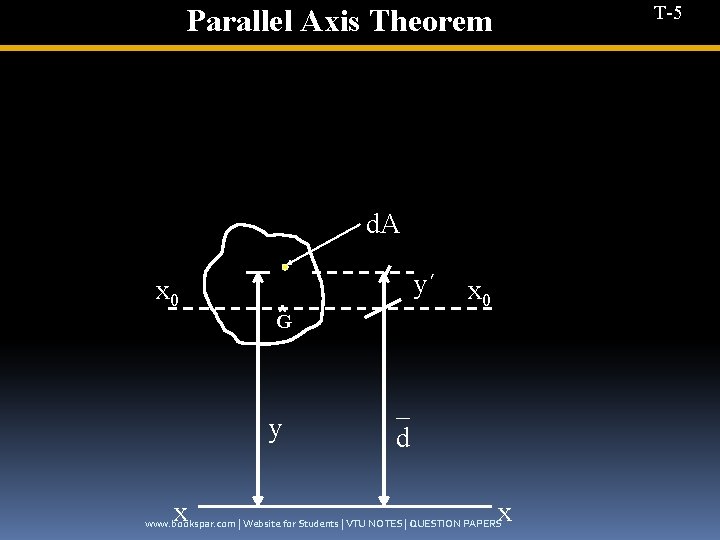
T-5 Parallel Axis Theorem d. A x 0 *G y x y´ x 0 _ d x www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

T-6 Ixx = ∫d. A. y 2 _ = ∫d. A (d +y')2 _ _ = ∫d. A (d 2+ y'2 + 2 dy') _ = ∫d. A. d 2 + ∫d. Ay΄2 + ∫ 2 d. d. Ay' _ 2 d 2 ∫d. A = A. (d) ∫d. A. y'2 = Ix 0 x 0 _ 2 d ∫ d. Ay’ = 0 ( since Ist moment of area about centroidal axis = 0) _ Ix x = Ix x +Ad 2 | Website for Students | VTU NOTES | QUESTION PAPERS 0 www. bookspar. com 0

T-7 Hence, moment of inertia of any area about an axis xx is equal to the M. I. about parallel centroidal axis plus the product of the total area and square of the distance between the two axes. Radius of Gyration It is the perpendicular distance at which the whole area may be assumed to be concentrated, yielding the same second moment of the area above the axis under consideration. www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

T-8 y Iyy = A. ryy 2 Ixx = A. rxx 2 A ryy = √ Iyy/A And rxx = √ Ixx /A A y rxx ryy x rxx and ryy are called the radii of gyration www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS x

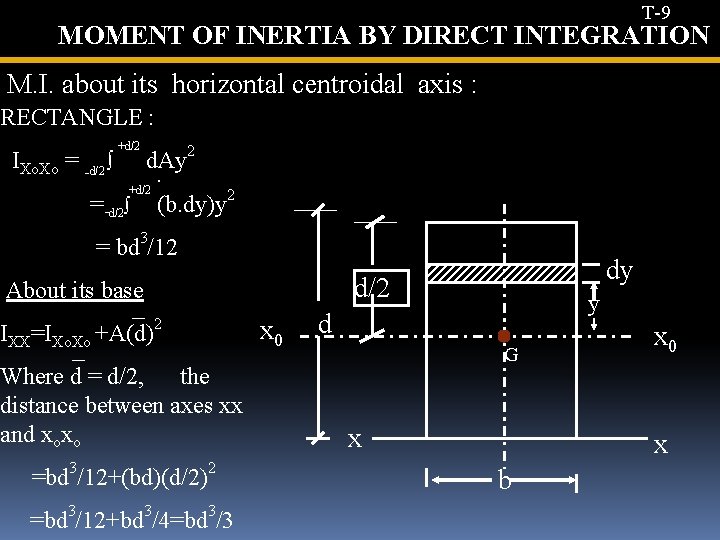
T-9 MOMENT OF INERTIA BY DIRECT INTEGRATION M. I. about its horizontal centroidal axis : RECTANGLE : +d/2 IXo. Xo = -d/2 ∫ d. Ay. +d/2 2 =-d/2∫ (b. dy)y 2 = bd 3/12 d/2 About its base IXX=IXo. Xo +A(d)2 x 0 Where d = d/2, the distance between axes xx and xoxo =bd 3/12+(bd)(d/2)2 =bd 3/12+bd 3/4=bd 3/3 dy y d G x x 0 x b

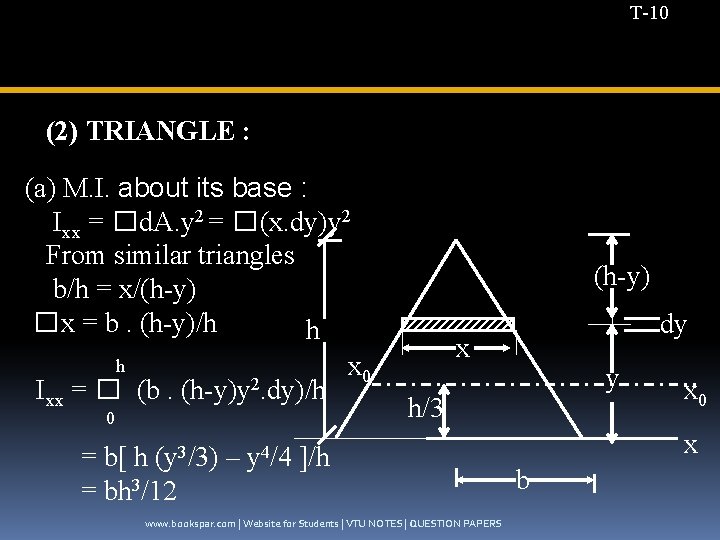
T-10 (2) TRIANGLE : (a) M. I. about its base : Ixx = � d. A. y 2 = � (x. dy)y 2 From similar triangles b/h = x/(h-y) � x = b. (h-y)/h h h x 0 I = � (b. (h-y)y 2. dy)/h xx 0 = b[ h (y 3/3) – y 4/4 ]/h = bh 3/12 (h-y) dy x y h/3 www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS x 0 x b

T-11 (b) Moment of inertia about its centroidal axis: _ Ixx = Ix x + Ad 2 0 0 _ Ix x = Ixx – Ad 2 0 0 = bh 3/12 – bh/2. (h/3)2 = bh 3/36 www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

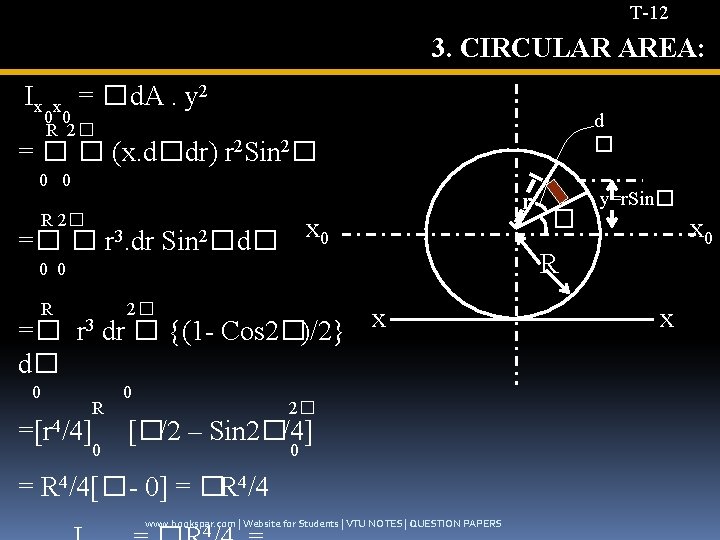
T-12 3. CIRCULAR AREA: Ix x = � d. A. y 2 0 0 R 2� d � = � � (x. d�. dr) r 2 Sin 2� 0 0 r R 2� =� � r 3. dr Sin 2� d� x 0 0 0 R 2� =� r 3 dr � {(1 - Cos 2�)/2} x 0 R x d� 0 R 0 2� =[r 4/4] [�/2 – Sin 2�/4] 0 0 = R 4/4[� - 0] = �R 4/4 www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS 4 � y=r. Sin� x

T-13 4. SEMI CIRCULAR AREA: Ixx = � d. A. y 2 R � = � � (r. d�. dr) r 2 Sin 2� 0 0 R � =� r 3. dr � Sin 2� d� y 0 0 R � =� � r 3 dr (1 - Cos 2�)/2) d� 0 0 � 4 R/3�x 0 x =[R 4/4] [�/2 – Sin 2�/4] 0 = R 4/4[�/2 - 0] = �R 4/8 www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS R x 0 x y 0

T-14 About horizontal centroidal axis: Ixx = Ix x + A(d)2 0 0 Ix 2 = I – A(d) xx x 0 0 = � R 4/8 �R 2/2. (4 R/3�)2 Ix 4 = 0. 11 R x 0 0 www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

T-15 QUARTER CIRCLE: y Ixx = Iyy R �/2 Ixx = � � (r. d�. dr). r 2 Sin 2� y 0 x 0 0 R �/2 =� r 3. dr � Sin 2� d� x 0 x 0 4 R/3π y y 0 R �/2 x =� r 3 dr � (1 - Cos 2�)/2) 4 R/3π d� 0 �/2 =[R 4/4] [�/2 – (Sin 2 �)/4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS 0

T-16 Moment of inertia about Centroidal axis, _ Ix x = Ixx - Ad 2 0 0 = �R 4/16 - �R 2. (0. 424 R)2 = 0. 055 R 4 The following table indicates the final values of M. I. about X and Y axes for different geometrical figures. www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

Sl. No Y 1 2 x 0 x Figure b d x 0 x d/2 Y Xo h x 0 x b 3 x 0 O y 0 x 0 x y y 0 Iy -y 0 0 I xx bd 3/12 - bd 3/3 - bh 3/36 - bh 3/12 - �R 4/4 - - 0. 11 R 4 �R 4/8 - 0. 055 R 4 �R 4/16 h/3 x x 0 4 R/3π x 0 x x 0 4 R/3π -x 0 0 y 0 R 4 5 Ix T-17 I yy 4 R/3π www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

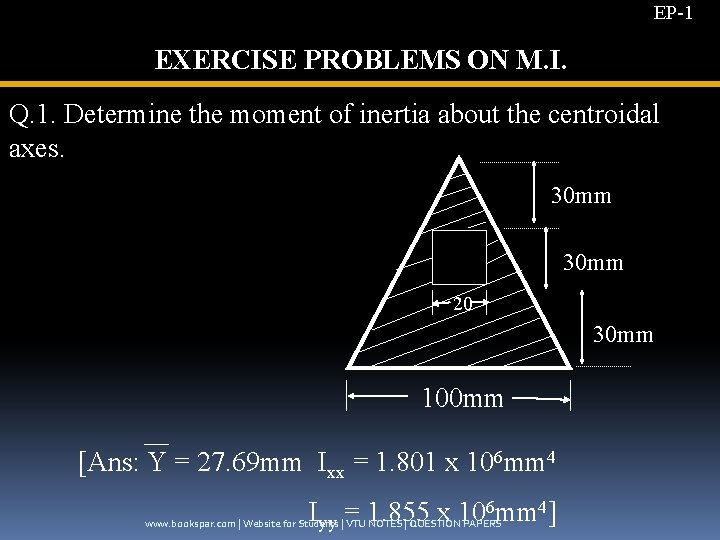
EP-1 EXERCISE PROBLEMS ON M. I. Q. 1. Determine the moment of inertia about the centroidal axes. 30 mm 20 30 mm 100 mm [Ans: Y = 27. 69 mm Ixx = 1. 801 x 106 mm 4 Iyy = 1. 855 x 106 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

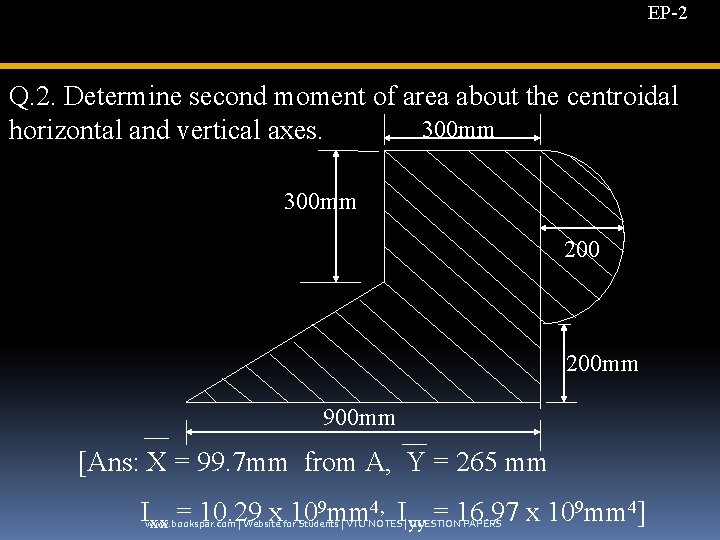
EP-2 Q. 2. Determine second moment of area about the centroidal 300 mm horizontal and vertical axes. 300 mm 200 mm 900 mm [Ans: X = 99. 7 mm from A, Y = 265 mm Ixx = 10. 29 x 109 mm 4, Iyy = 16. 97 x 109 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

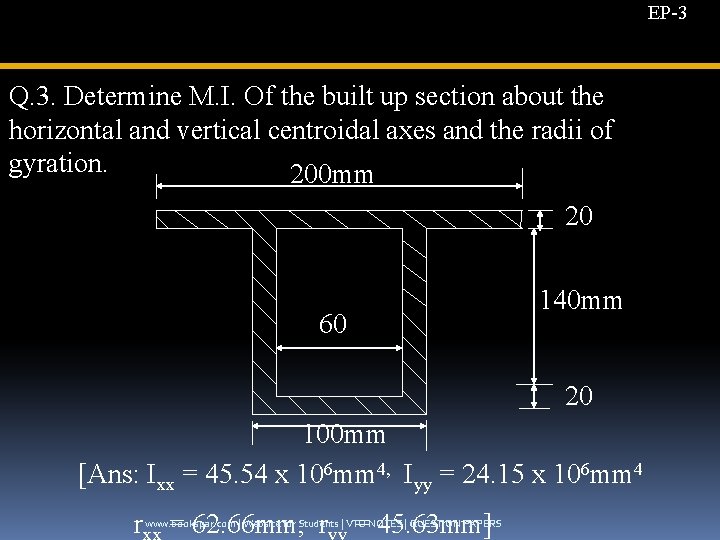
EP-3 Q. 3. Determine M. I. Of the built up section about the horizontal and vertical centroidal axes and the radii of gyration. 200 mm 20 60 140 mm 20 100 mm [Ans: Ixx = 45. 54 x 106 mm 4, Iyy = 24. 15 x 106 mm 4 r = 62. 66 mm, r = 45. 63 mm] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

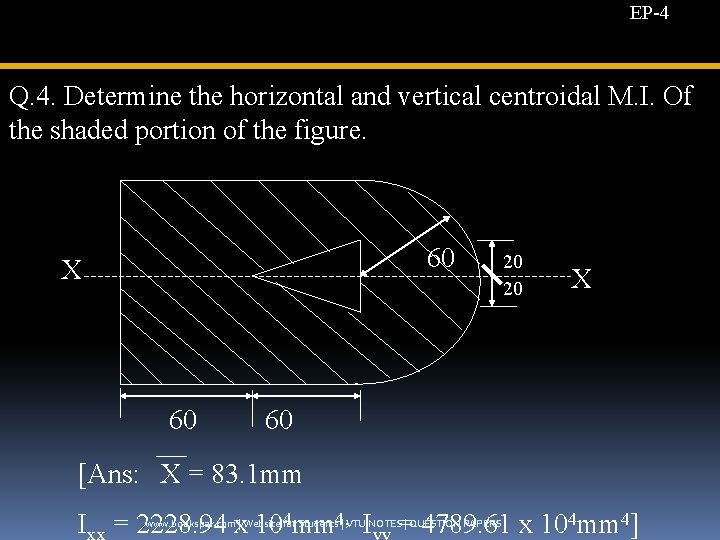
EP-4 Q. 4. Determine the horizontal and vertical centroidal M. I. Of the shaded portion of the figure. 60 X 60 20 20 X 60 [Ans: X = 83. 1 mm I = 2228. 94 x 104 mm 4, I = 4789. 61 x 104 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

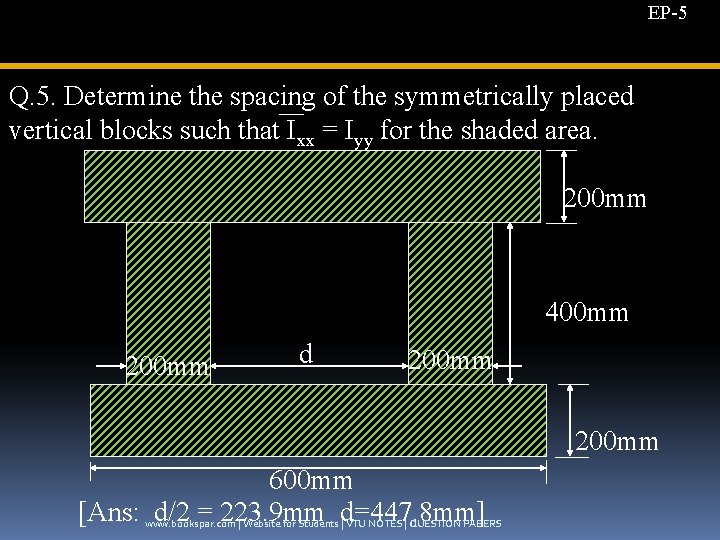
EP-5 Q. 5. Determine the spacing of the symmetrically placed vertical blocks such that Ixx = Iyy for the shaded area. 200 mm 400 mm 200 mm d 200 mm 600 mm [Ans: d/2 = 223. 9 mm d=447. 8 mm] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

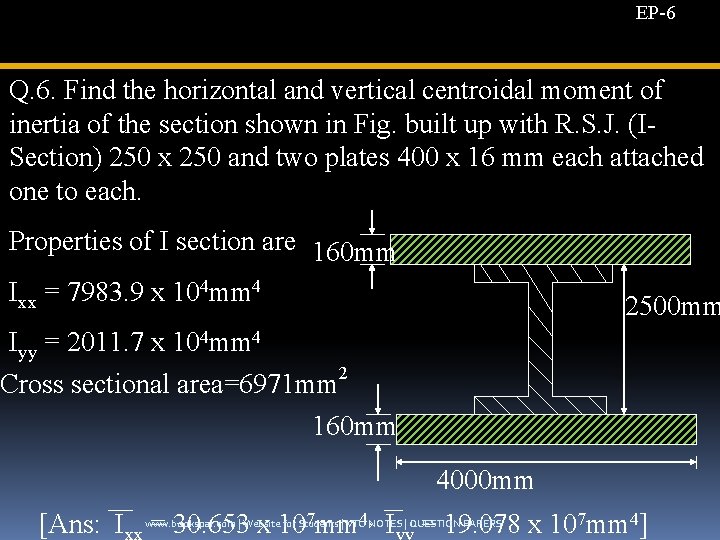
EP-6 Q. 6. Find the horizontal and vertical centroidal moment of inertia of the section shown in Fig. built up with R. S. J. (ISection) 250 x 250 and two plates 400 x 16 mm each attached one to each. Properties of I section are 160 mm Ixx = 7983. 9 x 104 mm 4 2500 mm Iyy = 2011. 7 x 104 mm 4 2 Cross sectional area=6971 mm 160 mm 4000 mm [Ans: I = 30. 653 x 107 mm 4, I = 19. 078 x 107 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

EP-7 Q. 7. Find the horizontal and vertical centroidal moment of inertia of built up section shown in Figure. The section consists of 4 symmetrically placed ISA 60 x 60 with two plates 300 x 20 mm 2. Properties of ISA Cross sectional area = 4400 mm 2 Ixx = Iyy ; Cxx = Cyy =18. 5 mm 200 mm 18. 5 mm 20 mm 300 mm [Ans: I = 111. 078 x 107 mm 4, I = 39. 574 x 107 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

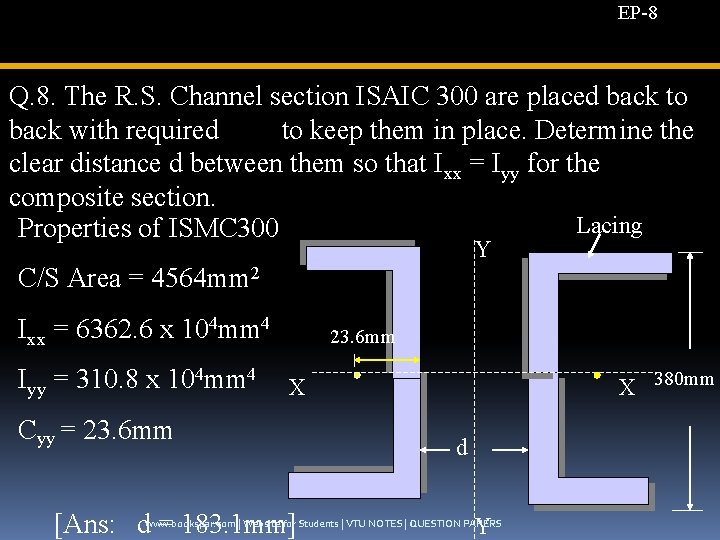
EP-8 Q. 8. The R. S. Channel section ISAIC 300 are placed back to back with required to keep them in place. Determine the clear distance d between them so that Ixx = Iyy for the composite section. Lacing Properties of ISMC 300 Y C/S Area = 4564 mm 2 Ixx = 6362. 6 x 104 mm 4 Iyy = 310. 8 x 104 mm 4 23. 6 mm X 380 mm X Cyy = 23. 6 mm [Ans: d = 183. 1 mm] d Y www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS

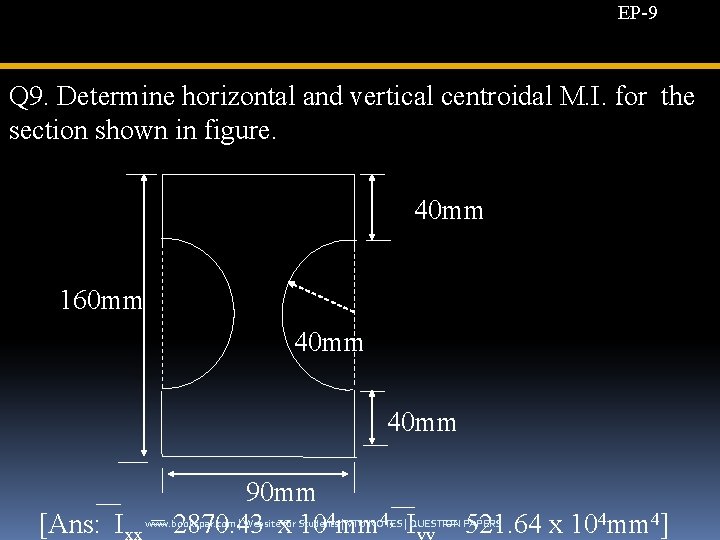
EP-9 Q 9. Determine horizontal and vertical centroidal M. I. for the section shown in figure. 40 mm 160 mm 40 mm 90 mm [Ans: I = 2870. 43 x 104 mm 4, I = 521. 64 x 104 mm 4] www. bookspar. com | Website for Students | VTU NOTES | QUESTION PAPERS