T1 MOMENT OF INERTIA Moment of Inertia The

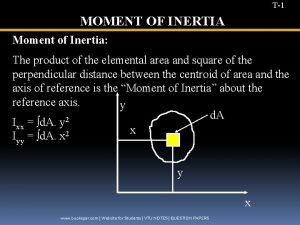
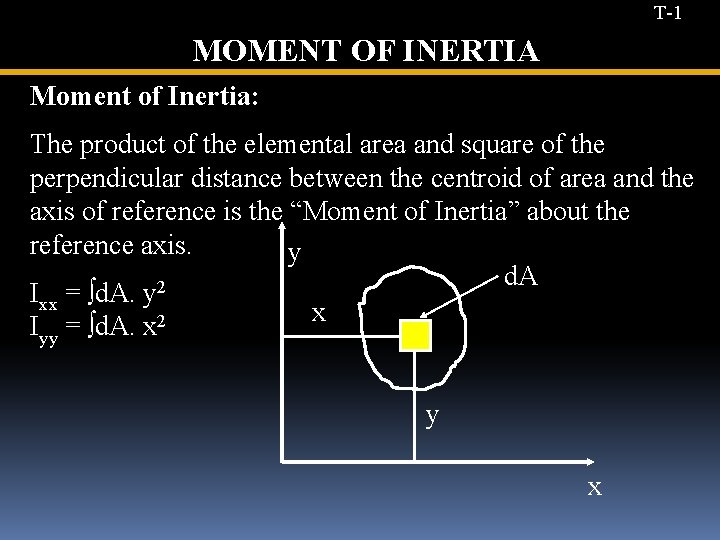
T-1 MOMENT OF INERTIA Moment of Inertia: The product of the elemental area and square of the perpendicular distance between the centroid of area and the axis of reference is the “Moment of Inertia” about the reference axis. y d. A 2 Ixx = ∫d. A. y x Iyy = ∫d. A. x 2 y x

T-2 It is also called second moment of area because first moment of elemental area is d. A. y and d. A. x; and if it is again multiplied by the distance, we get second moment of elemental area as (d. A. y)y and (d. A. x)x.

T-3 Polar moment of Inertia (Perpendicular Axes theorem) The moment of inertia of an area about an axis perpendicular to the plane of the area is called “Polar Moment of Inertia” and it is denoted by symbol Izz or J or Ip. The moment of inertia of an area in xy plane w. r. to z. axis is Izz = Ip = J = ∫r 2 d. A = ∫(x 2 + y 2) d. A = ∫x 2 d. A + ∫y 2 d. A = Ixx +Iyy Y x r y O x z

T-4 PERPENDICULAR AXIS THEOREM Hence polar M. I. for an area w. r. t. an axis perpendicular to its plane of area is equal to the sum of the M. I. about any two mutually perpendicular axes in its plane, passing through the point of intersection of the polar axis and the area.

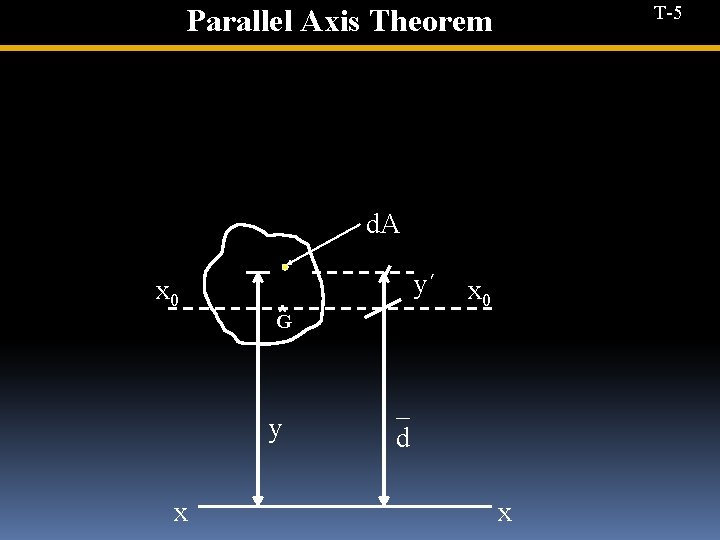
T-5 Parallel Axis Theorem d. A x 0 *G y x y´ x 0 _ d x

T-6 Ixx = ∫d. A. y 2 _ = ∫d. A (d +y')2 _ _ = ∫d. A (d 2+ y'2 + 2 dy') _ = ∫d. A. d 2 + ∫d. Ay΄2 + ∫ 2 d. d. Ay' _ 2 d 2 ∫d. A = A. (d) ∫d. A. y'2 = Ix 0 x 0 _ 2 d ∫ d. Ay’ = 0 ( since Ist moment of area about centroidal axis = 0) _ Ix x = Ix x +Ad 2 0 0

T-7 Hence, moment of inertia of any area about an axis xx is equal to the M. I. about parallel centroidal axis plus the product of the total area and square of the distance between the two axes. Radius of Gyration It is the perpendicular distance at which the whole area may be assumed to be concentrated, yielding the same second moment of the area above the axis under consideration.

T-8 Iyy = A. ryy 2 Ixx = A. rxx 2 y A ryy = √ Iyy/A And rxx = √ Ixx /A A y rxx ryy x rxx and ryy are called the radii of gyration x

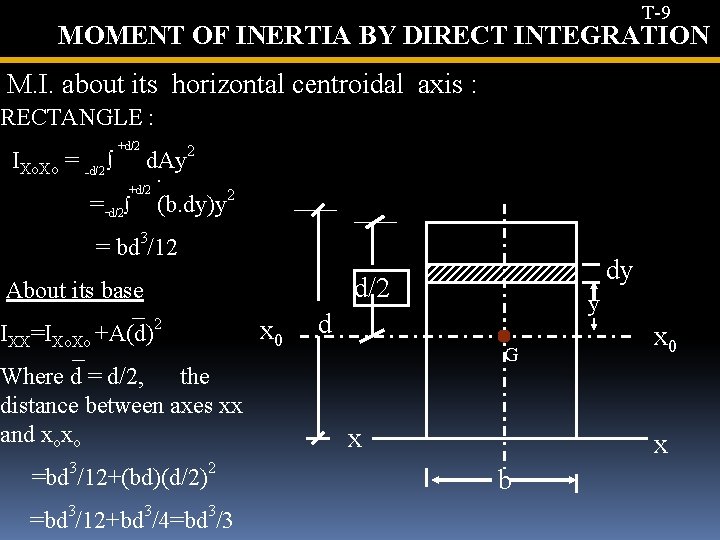
T-9 MOMENT OF INERTIA BY DIRECT INTEGRATION M. I. about its horizontal centroidal axis : RECTANGLE : +d/2 IXo. Xo = -d/2 ∫ d. Ay. +d/2 2 =-d/2∫ (b. dy)y 2 = bd 3/12 d/2 About its base IXX=IXo. Xo +A(d)2 x 0 Where d = d/2, the distance between axes xx and xoxo =bd 3/12+(bd)(d/2)2 =bd 3/12+bd 3/4=bd 3/3 dy y d G x x 0 x b

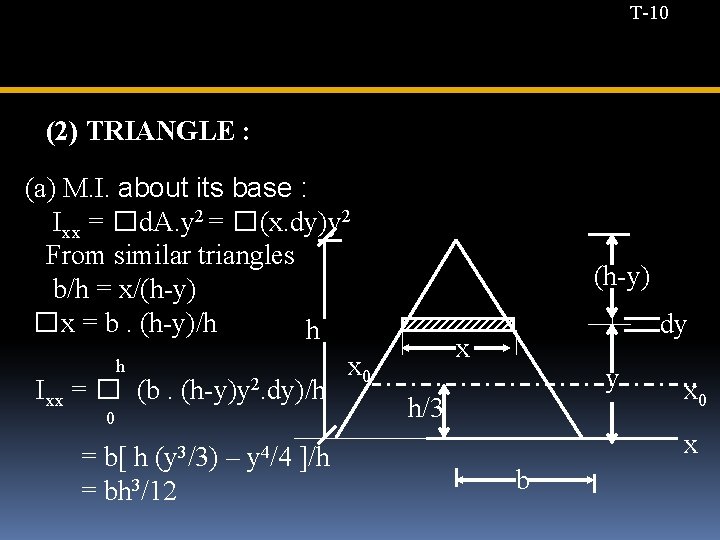
T-10 (2) TRIANGLE : (a) M. I. about its base : Ixx = � d. A. y 2 = � (x. dy)y 2 From similar triangles b/h = x/(h-y) � x = b. (h-y)/h h h x 0 I = � (b. (h-y)y 2. dy)/h xx 0 = b[ h (y 3/3) – y 4/4 ]/h = bh 3/12 (h-y) dy x y h/3 x 0 x b

T-11 (b) Moment of inertia about its centroidal axis: _ Ixx = Ix x + Ad 2 0 0 _ Ix x = Ixx – Ad 2 0 0 = bh 3/12 – bh/2. (h/3)2 = bh 3/36

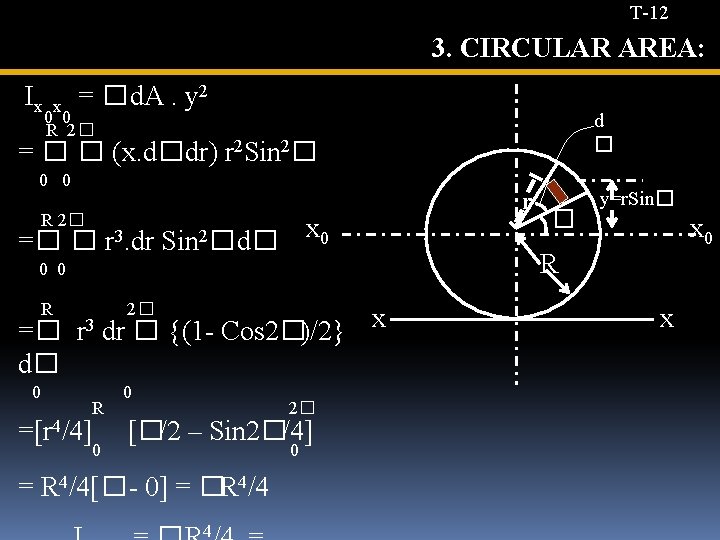
T-12 3. CIRCULAR AREA: Ix x = � d. A. y 2 0 0 R 2� d � = � � (x. d�. dr) r 2 Sin 2� 0 0 r R 2� =� � r 3. dr Sin 2� d� x 0 0 0 R 2� =� r 3 dr � {(1 - Cos 2�)/2} d� 0 R 0 2� =[r 4/4] [�/2 – Sin 2�/4] 0 0 = R 4/4[� - 0] = �R 4/4 4 � y=r. Sin� x 0 R x x

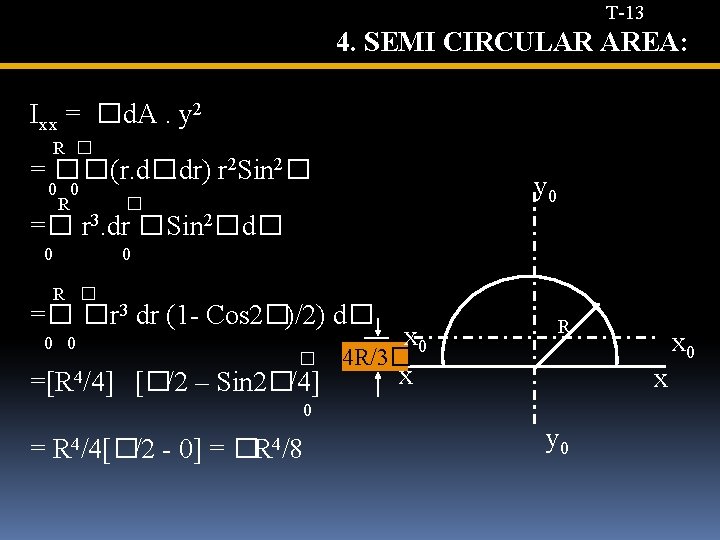
T-13 4. SEMI CIRCULAR AREA: Ixx = � d. A. y 2 R � = � � (r. d�. dr) r 2 Sin 2� 0 0 R � =� r 3. dr � Sin 2� d� y 0 0 R � =� � r 3 dr (1 - Cos 2�)/2) d� 0 0 � 4 R/3�x 0 x =[R 4/4] [�/2 – Sin 2�/4] 0 = R 4/4[�/2 - 0] = �R 4/8 R x 0 x y 0

T-14 About horizontal centroidal axis: Ixx = Ix x + A(d)2 0 0 Ix 2 = I – A(d) xx x 0 0 = � R 4/8 �R 2/2. (4 R/3�)2 Ix 4 = 0. 11 R x 0 0

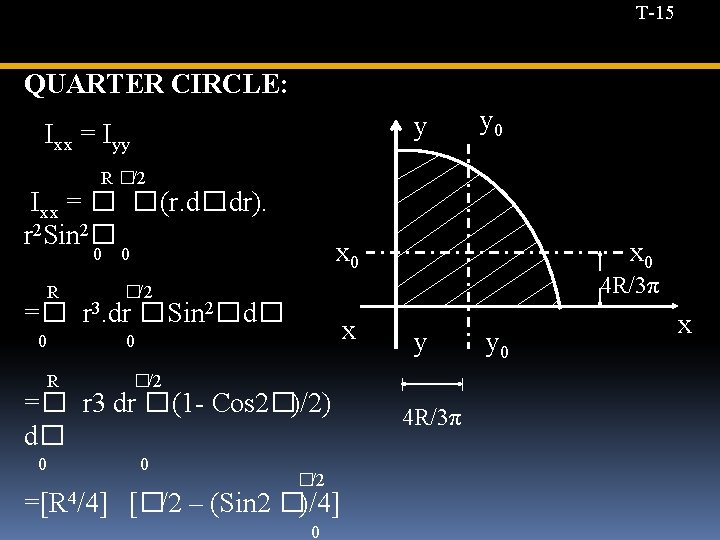
T-15 QUARTER CIRCLE: y Ixx = Iyy R �/2 Ixx = � � (r. d�. dr). r 2 Sin 2� y 0 x 0 0 R �/2 =� r 3. dr � Sin 2� d� x 0 R �/2 x 0 4 R/3π y y 0 x =� r 3 dr � (1 - Cos 2�)/2) 4 R/3π d� 0 �/2 =[R 4/4] [�/2 – (Sin 2 �)/4] 0

T-16 Moment of inertia about Centroidal axis, _ Ix x = Ixx - Ad 2 0 0 = �R 4/16 - �R 2. (0. 424 R)2 = 0. 055 R 4 The following table indicates the final values of M. I. about X and Y axes for different geometrical figures.

Sl. No Y 1 2 x 0 x Figure b d x 0 x d/2 Y Xo h x 0 x b 3 x 0 O y 0 x 0 x y y 0 Iy -y 0 0 I xx bd 3/12 - bd 3/3 - bh 3/36 - bh 3/12 - �R 4/4 - - 0. 11 R 4 �R 4/8 - 0. 055 R 4 �R 4/16 h/3 x x 0 4 R/3π x 0 x x 0 4 R/3π -x 0 0 y 0 R 4 5 Ix T-17 I yy 4 R/3π