Moment of Inertia Lecture 10 Moment it is

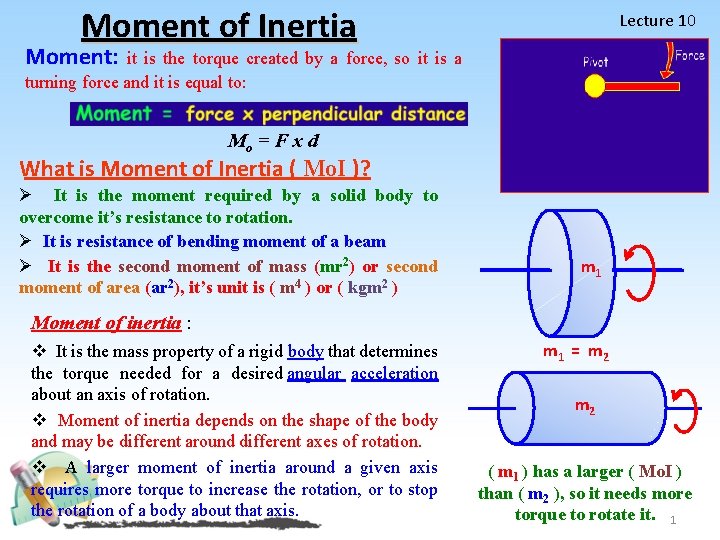
Moment of Inertia Lecture 10 Moment: it is the torque created by a force, so it is a turning force and it is equal to: Mo = F x d What is Moment of Inertia ( Mo. I )? Ø It is the moment required by a solid body to overcome it’s resistance to rotation. Ø It is resistance of bending moment of a beam Ø It is the second moment of mass (mr 2) or second moment of area (ar 2), it’s unit is ( m 4 ) or ( kgm 2 ) m 1 Moment of inertia : v It is the mass property of a rigid body that determines the torque needed for a desired angular acceleration about an axis of rotation. v Moment of inertia depends on the shape of the body and may be different around different axes of rotation. v A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation of a body about that axis. m 1 = m 2 ( m 1 ) has a larger ( Mo. I ) than ( m 2 ), so it needs more torque to rotate it. 1

Moment of Inertia for Area Ø To understand the concept of ( Mo. I ) for Area, lets Consider a plate submerged in a liquid. Ø The pressure of a liquid at a distance z below the surface is given by: Lecture 10 Liquid surface p = . z where: is the specific weight of the liquid. v The force on the area ( d. A ) at that point is: d. F = p. d. A v The moment about the x-axis due to this force is [ z. (d. F) ], the total moment is: A z. d. F = A z. P. d. A = A . z 2. d. A = . A( z 2. d. A ) = . Iwhere: the integral term is referred to as the moment of inertial of the area of the plate about an axis. A( z 2. d. A ) = I = the moment of inertia for area or the second moment for area This sort of integral term also appears in solid mechanics ( strength of material ) when determining stresses and deflection. 2

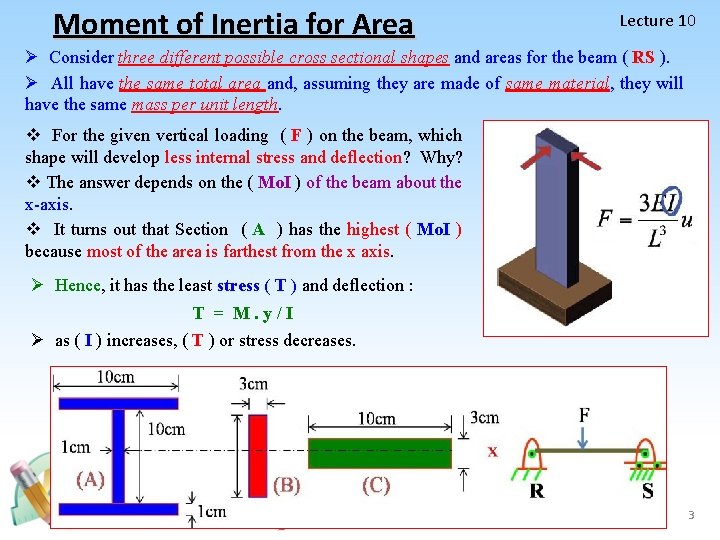
Moment of Inertia for Area Lecture 10 Ø Consider three different possible cross sectional shapes and areas for the beam ( RS ). Ø All have the same total area and, assuming they are made of same material, they will have the same mass per unit length. v For the given vertical loading ( F ) on the beam, which shape will develop less internal stress and deflection? Why? v The answer depends on the ( Mo. I ) of the beam about the x-axis. v It turns out that Section ( A ) has the highest ( Mo. I ) because most of the area is farthest from the x axis. Ø Hence, it has the least stress ( T ) and deflection : T = M. y/I Ø as ( I ) increases, ( T ) or stress decreases. 3

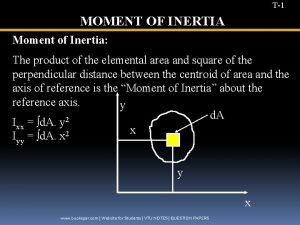
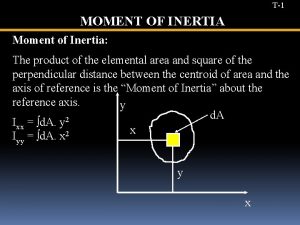
Moment of Inertia for Area Lecture 10 The Rectangular moments of inertia Ix and Iy of an area are defined as: Ø For the differential area ( d. A ), shown in the figure: d Ix d Iy = = y 2. d. A x 2. d. A The Polar moments of inertia Ix and Iy of an area are defined as: d JO = r 2. d. A = ( x 2 + y 2 ). d. A d JO = x 2. d. A + y 2. d. A d JO = d I x + d I y where: ( JO ) is the polar moment of inertia about the pole ( O ) or ( z axis ). v The moments of inertia for the entire area are obtained by integration. JO Ix = A y 2. d. A ; Iy = A x 2. d. A = A r 2. d. A = A ( x 2 + y 2 ). d. A = Ix + Iy v The ( Mo. I ) is also referred to as the second moment of an area and has units of length to the fourth power (m 4 or in 4). 4

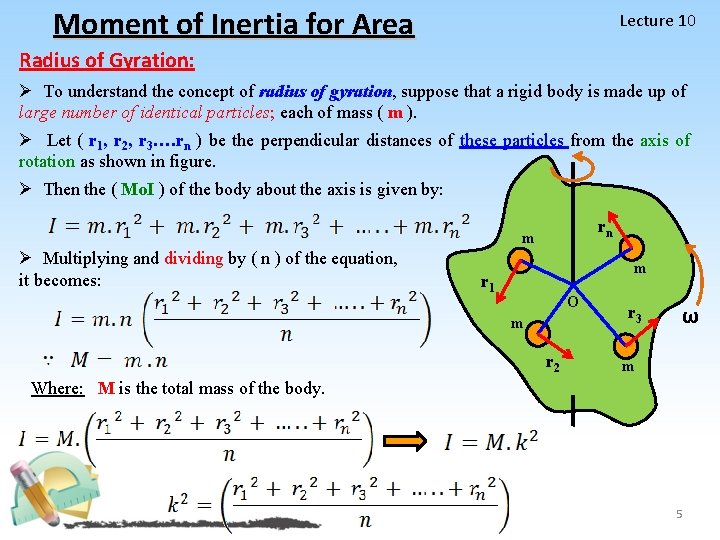
Moment of Inertia for Area Lecture 10 Radius of Gyration: Ø To understand the concept of radius of gyration, suppose that a rigid body is made up of large number of identical particles; each of mass ( m ). Ø Let ( r 1, r 2, r 3…. rn ) be the perpendicular distances of these particles from the axis of rotation as shown in figure. Ø Then the ( Mo. I ) of the body about the axis is given by: rn m Ø Multiplying and dividing by ( n ) of the equation, it becomes: m r 1 O m r 2 r 3 ω m Where: M is the total mass of the body. 5

Moment of Inertia for Area Lecture 10 v The radius of gyration of an area ( A ) with respect to the ( x axis ) is defined as the distance ( kx ). where: Ix = k x. A v With similar definitions for the radii of gyration of ( A ) with respect to the ( y axis ) and with respect to ( O ), we have: Parallel - Axis Theorem for an Area: Ø This theorem relates the moment of inertia (Mo. I) of an area about an axis passing through the area’s centroid to the ( Mo. I ) of the area about a corresponding parallel axis. Ø This theorem has many practical applications, especially when working with composite areas. Ø Consider an area with centroid ( C ). The ( x' and y' ) axes pass through ( C ). 6

Parallel - Axis Theorem for an Area: Lecture 10 v The ( Mo. I ) about the ( x-axis ), which is parallel to, and with distance ( dy ) from the ( x ' axis ), is found by using the parallel-axis theorem. IX = A y 2 d. A = A (y' + dy)2 d. A = A y' 2 d. A + 2 dy A y' d. A + dy 2 A d. A Using the definition of the centroid: y' = y’ + dy ( A y' d. A) / ( A d. A) Now, since ( C ) is at the origin of the ( x' – y‘ axes ): y' = 0 , Thus: and hence, IX = I X ' + A d y 2 A y' d. A = 0 Similarly, IY = I Y ' + A d X 2 Ø The polar moment of inertia ( JO ) of an area about (O ) and the polar moment of inertia ( JC ) of the area about its centroid are related to the distance ( d ) between points (C ) and (O ) by the relationship: JO = JC + Ad 2 Ø The parallel-axis theorem is used very effectively to compute the moment of inertia of a composite area with respect to a given axis. 7

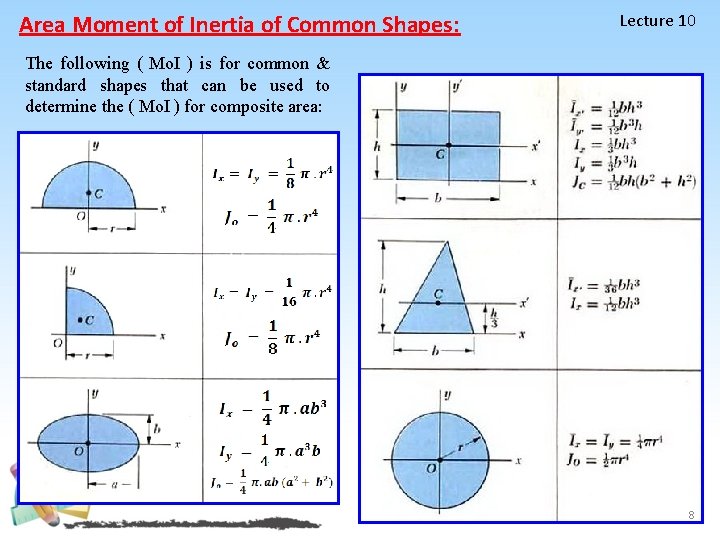
Area Moment of Inertia of Common Shapes: Lecture 10 The following ( Mo. I ) is for common & standard shapes that can be used to determine the ( Mo. I ) for composite area: 8

Lecture 10 Mo. I for an Area by Integration: Ø For simplicity, the area element used has a differential size in only one direction ( dx or dy ). Ø This results in a single integration and is usually simpler than doing a double integration with two differentials ( dx and dy ). The step-by-step procedure is: 1. Choose the element d. A: There are two choices a vertical strip or a horizontal strip. Some considerations about this choice are: x a) The element parallel to the axis about which the ( Mo. I ) is to be determined usually results in an easier solution. For example, it is typically choose a horizontal strip for determining ( Ix ) and a vertical strip for determining ( Iy ). b) If ( y ) is easily expressed in terms of x (e. g. , y = x 2 + 1), then choosing a vertical strip with a differential element ( dx ) wide may be advantageous. 2. Integrate to find the ( Mo. I ). For example, given the element shown in the figure above: Iy = x 2 d. A = x 2 y dx Ix = d Ix = (1 / 3) y 3 dx 9

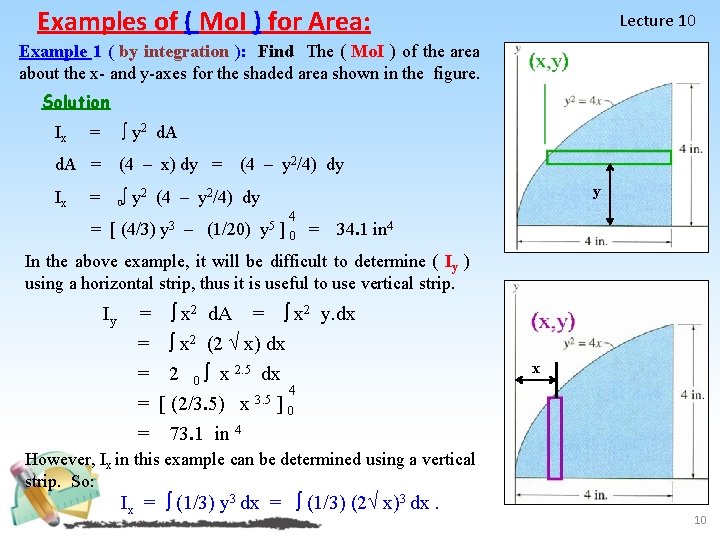
Examples of ( Mo. I ) for Area: Lecture 10 Example 1 ( by integration ): Find The ( Mo. I ) of the area about the x- and y-axes for the shaded area shown in the figure. Solution Ix y 2 d. A = (4 – x) dy = Ix 0 = (4 – y 2/4) dy y y 2 (4 – y 2/4) dy 4 = [ (4/3) y 3 – (1/20) y 5 ] 0 = 34. 1 in 4 In the above example, it will be difficult to determine ( Iy ) using a horizontal strip, thus it is useful to use vertical strip. Iy = = = x 2 d. A = x 2 y. dx x 2 (2 x) dx 2 0 x 2. 5 dx 4 3. 5 [ (2/3. 5) x ] 0 73. 1 in 4 x However, Ix in this example can be determined using a vertical strip. So: Ix = (1/3) y 3 dx = (1/3) (2 x)3 dx. 10

Example 2 ( by integration ): (a) Determine the centroidal polar moment of inertia of a circular area by direct integration. (b) Using the result of part a, determine the moment of inertia of a circular area with respect to a diameter. Solution Lecture 10 x x 11

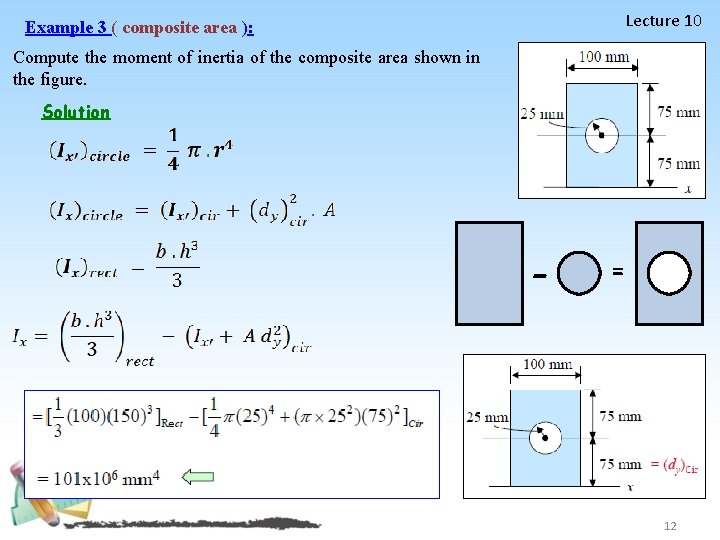
Lecture 10 Example 3 ( composite area ): Compute the moment of inertia of the composite area shown in the figure. Solution = 12

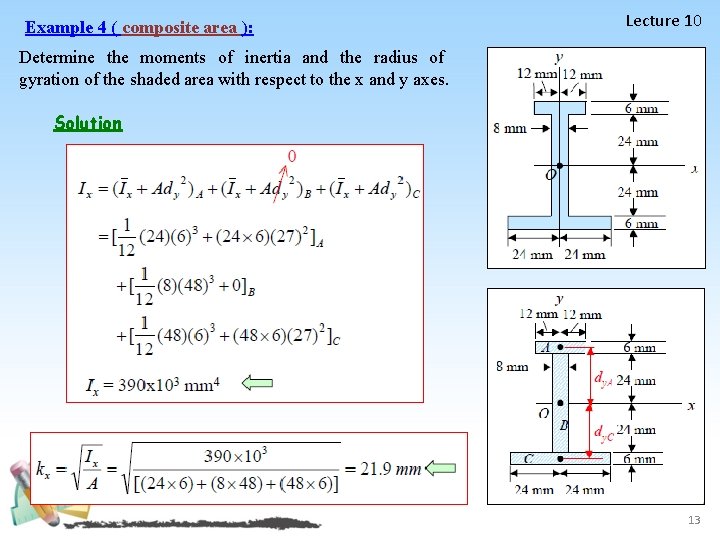
Example 4 ( composite area ): Lecture 10 Determine the moments of inertia and the radius of gyration of the shaded area with respect to the x and y axes. Solution 13

Continue Example 4 ( composite area ): Lecture 10 14