Rotational Inertia Kinetic Energy Linear Angular Linear Angular

Rotational Inertia & Kinetic Energy

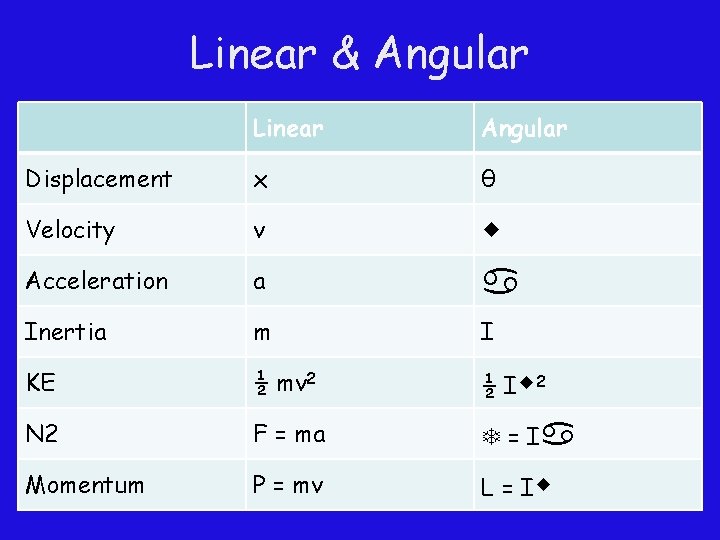
Linear & Angular Linear Angular Displacement x θ Velocity v Acceleration a Inertia m I KE ½ mv 2 ½ I 2 N 2 F = ma = I Momentum P = mv L = I

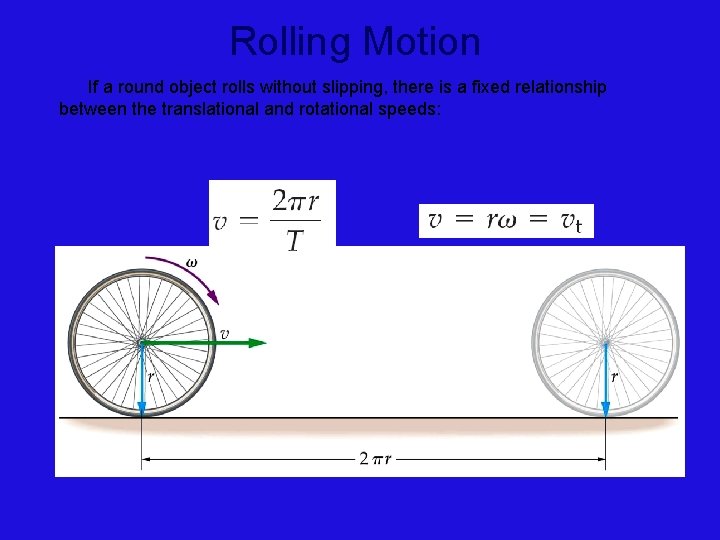
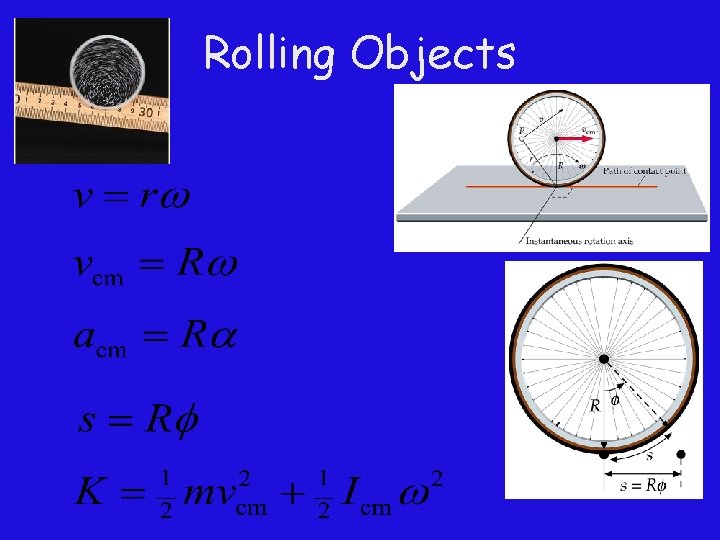
Rolling Motion If a round object rolls without slipping, there is a fixed relationship between the translational and rotational speeds:

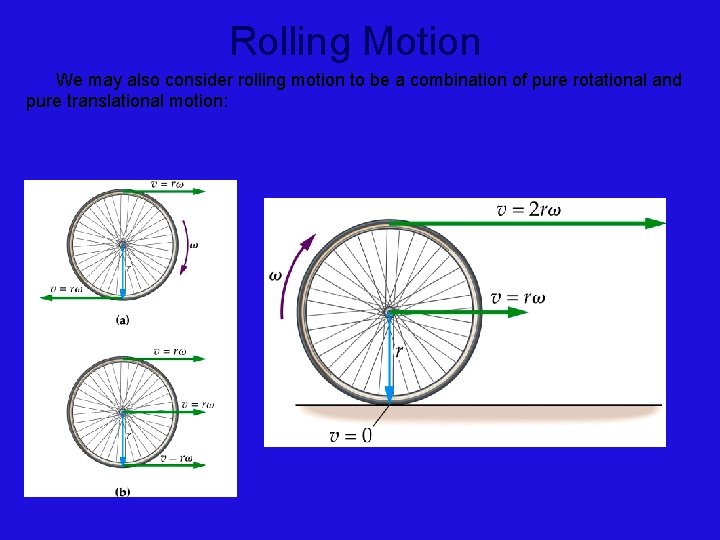
Rolling Motion We may also consider rolling motion to be a combination of pure rotational and pure translational motion:

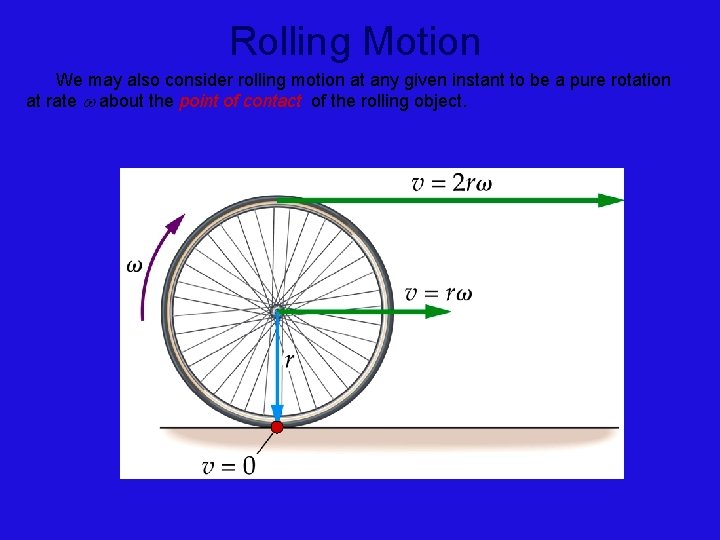
Rolling Motion We may also consider rolling motion at any given instant to be a pure rotation at rate w about the point of contact of the rolling object.

A Rolling Tire A car with tires of radius 32 cm drives on a highway at a speed of 55 mph. (a) What is the angular speed w of the tires? (b) What is the linear speed vtop of the top to the tires?

Rotational Kinetic Energy • Consider a mass M on the end of a string being spun around in a circle with radius r and angular frequency w – Mass has speed v = w r – Mass has kinetic energy M • K = ½ M v 2 • K = ½ M w 2 r 2 • Rotational Kinetic Energy is energy due to circular motion of object. 24

Rotational Inertia I • Tells how much “work” is required to get object spinning. Just like mass tells you how much “work” is required to get object moving. – Ktran = ½ m v 2 Linear Motion – Krot = ½ I w 2 Rotational Motion 13

Inertia Rods Two batons have equal mass and length. Which will be “easier” to spin? A) Mass on ends B) Same C) Mass in center I = S m r 2 Further mass is from axis of rotation, greater moment of inertia (harder to spin)

Inertia of a Dumbbell Use the definition of moment of inertia to calculate that of a dumbbell-shaped object with two point masses m separated by a distance of 2 r and rotating about a perpendicular axis through their center of symmetry. If the rod has mass then +Irod=1/12

Nose to the Grindstone A grindstone of radius r = 0. 610 m is being used to sharpen an axe. If the linear speed of the stone is 1. 50 m/s and the stone’s kinetic energy is 13. 0 J, what is its moment of inertia I ?

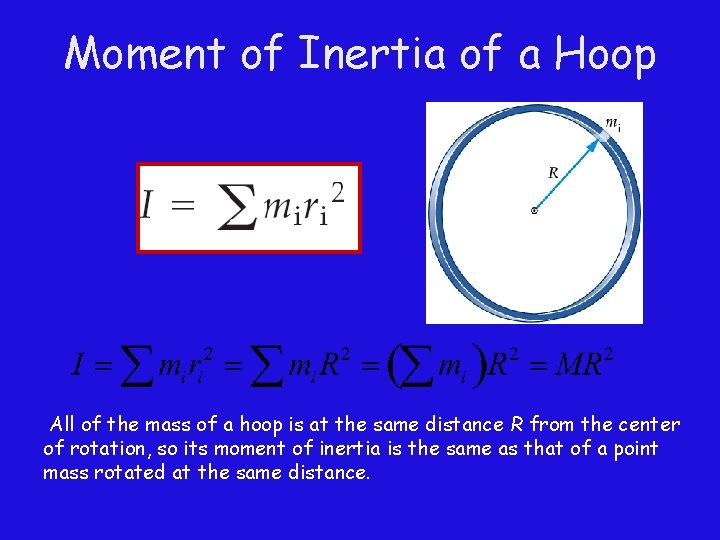
Moment of Inertia of a Hoop All of the mass of a hoop is at the same distance R from the center of rotation, so its moment of inertia is the same as that of a point mass rotated at the same distance.

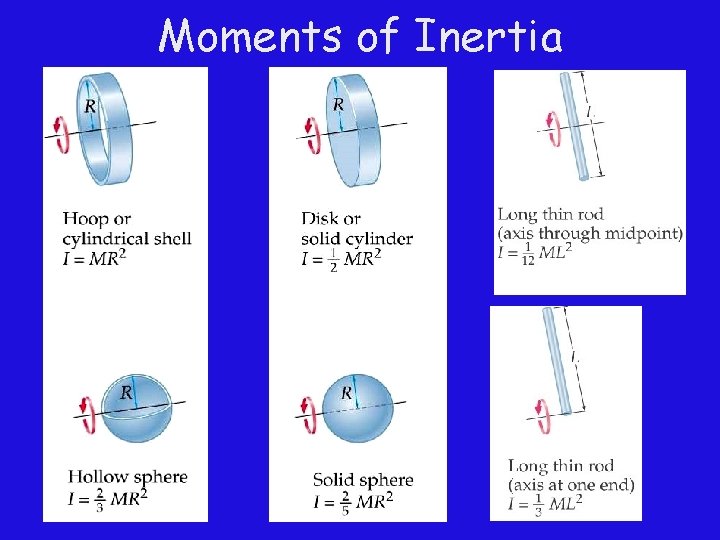
Moments of Inertia

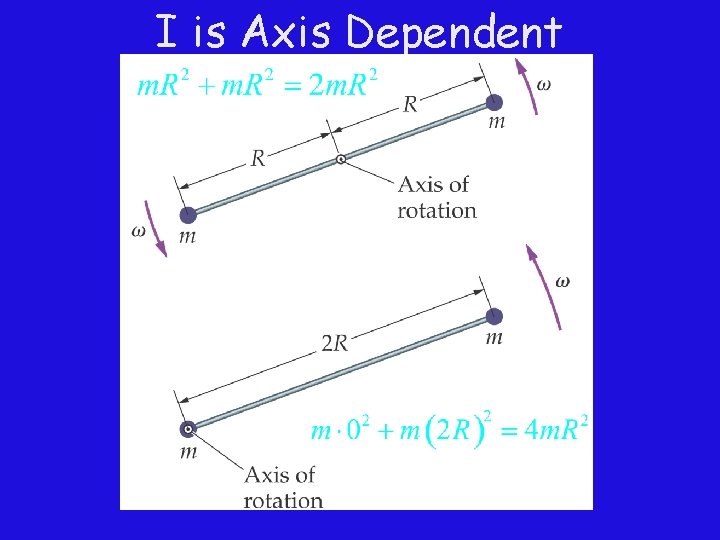
I is Axis Dependent

Rolling Objects

Like a Rolling Disk A 1. 20 kg disk with a radius 0 f 10. 0 cm rolls without slipping. The linear speed of the disk is v = 1. 41 m/s. (a) Find the translational kinetic energy. (b) Find the rotational kinetic energy. (c) Find the total kinetic energy.

Preflight: Rolling Race (Hoop vs Cylinder) A hoop and a cylinder of equal mass roll down a ramp with height h. Which has greatest KE at bottom? A) Hoop B) Same C) Cylinder 20% 50% 30%

Preflight: Rolling Race (Hoop vs Cylinder) A hoop and a cylinder of equal mass roll down a ramp with height h. Which has greatest speed at the bottom of the ramp? A) Hoop B) Same C) Cylinder I = MR 2 I = ½ MR 2

Rolling Down an Incline 0 0

Spinning Wheel A block is attached to a string around a pulley. The string is pulled rising the block at a velocity v spinning the pulley with a rotational velocity w. To what height h does the block rise? mgh=1/2 mv 2(1+I/m. R 2)

A Bowling Ball A bowling ball that has an 11 cm radius and a 5. 0 kg mass is rolling without slipping at 2. 0 m/s on a horizontal ball return. It continues to roll without slipping up a hill to a height h before momentarily coming to rest and then rolling back down the hill. Model the bowling ball as a uniform sphere and calculate h.

Torque and Energy • • Remember Torque=Fd=Iα A torque makes an acceleration ω=αt • So with an initial torque you can spin something up and that can roll to do work.

Example • A torque of 5. 0 Nm is applied to a 1. 0 kg disk with a 50. cm radius for 5. 0 seconds. • What is the initial ω? • If the coefficient of rolling friction is μ=. 05 use work to find how far the wheel rolls.

Example • A torque of 5. 0 Nm is applied to a 1. 0 kg disk with a 50. cm radius for 5. 0 seconds. • What is the initial ω? • ω=αt τ=Iα so α= τ/I • ω=t (τ/I) Idisk= 1/2 mr 2 • ω=t (τ/(1/2 mr 2)) • ω=5 (5/(1/2*1*. 52)) = 200 rad/s 2

Example • A torque of 5. 0 Nm is applied to a 1. 0 kg disk with a 50. cm radius for 5. 0 seconds. • If the coefficient of rolling friction is μ=. 05 use work to find how far the wheel rolls. • ω=200 rad/s 2 KE=1/2 mv 2 + 1/2 Iω2 • v= ωr Idisk= 1/2 mr 2 KE=1/2 m(ωr)2 + ½(1/2 mr 2)ω2 • KE=3/4 m(ωr)2 =. 75*1*(200*. 5)2 = 7, 500 J