Chapter 10 Rotation 10 1 What is Physics




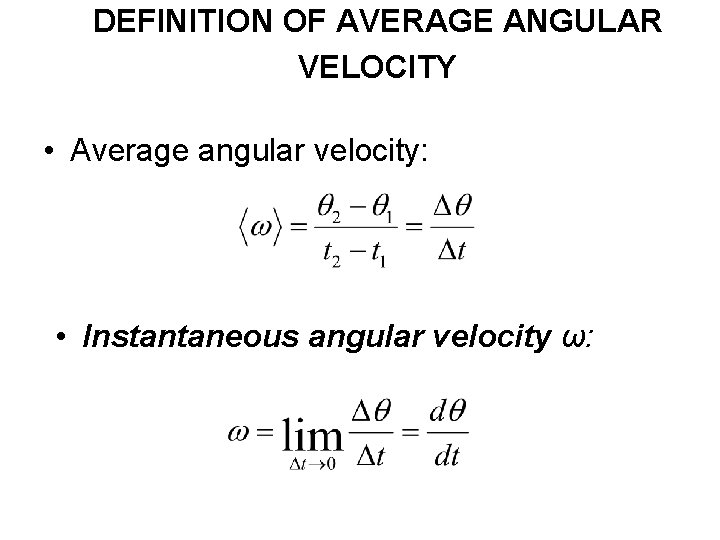





















- Slides: 46

Chapter 10. Rotation 10. 1. What is Physics? 10. 2. The Rotational Variables 10. 3. Are Angular Quantities Vectors? 10. 4. Rotation with Constant Angular Acceleration 10. 5. Relating the Linear and Angular Variables 10. 6. Kinetic Energy of Rotation 10. 7. Calculating the Rotational Inertia 10. 8. Torque 10. 9. Newton's Second Law for Rotation 10. Work and Rotational Kinetic Energy

Translation and Rotation

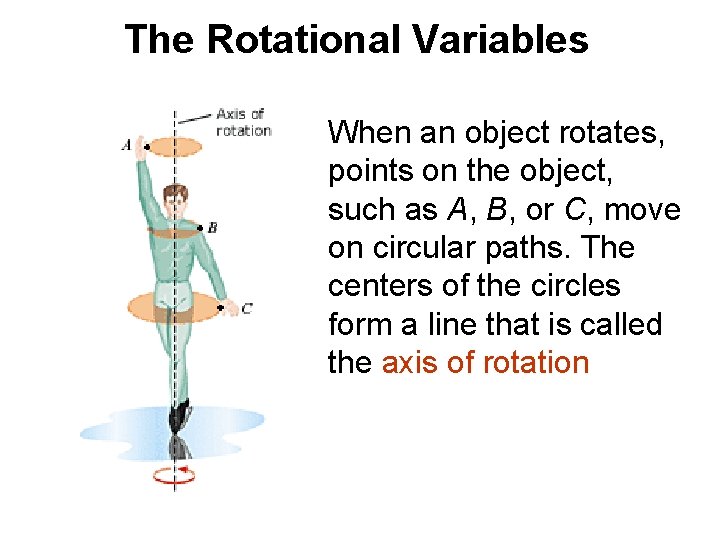
The Rotational Variables When an object rotates, points on the object, such as A, B, or C, move on circular paths. The centers of the circles form a line that is called the axis of rotation

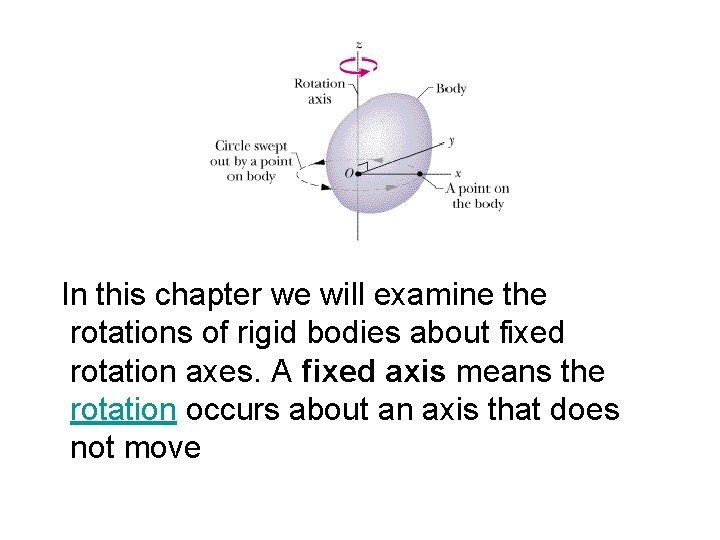
In this chapter we will examine the rotations of rigid bodies about fixed rotation axes. A fixed axis means the rotation occurs about an axis that does not move

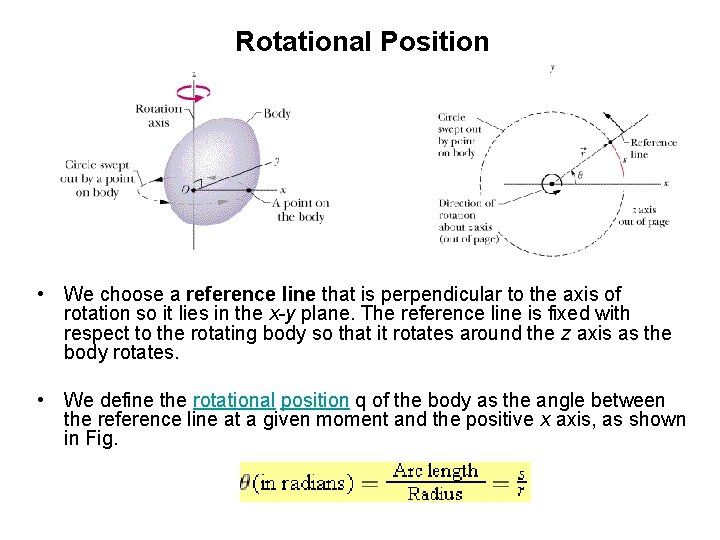
Rotational Position • We choose a reference line that is perpendicular to the axis of rotation so it lies in the x-y plane. The reference line is fixed with respect to the rotating body so that it rotates around the z axis as the body rotates. • We define the rotational position q of the body as the angle between the reference line at a given moment and the positive x axis, as shown in Fig.

DEFINITION OF ANGULAR DISPLACEMENT • When a rigid body rotates about a fixed axis, the angular displacement is the angle Δθ= - 0 swept out by a line passing through any point on the body and intersecting the axis of rotation perpendicularly. • SI Unit of Angular Displacement: radian (rad)

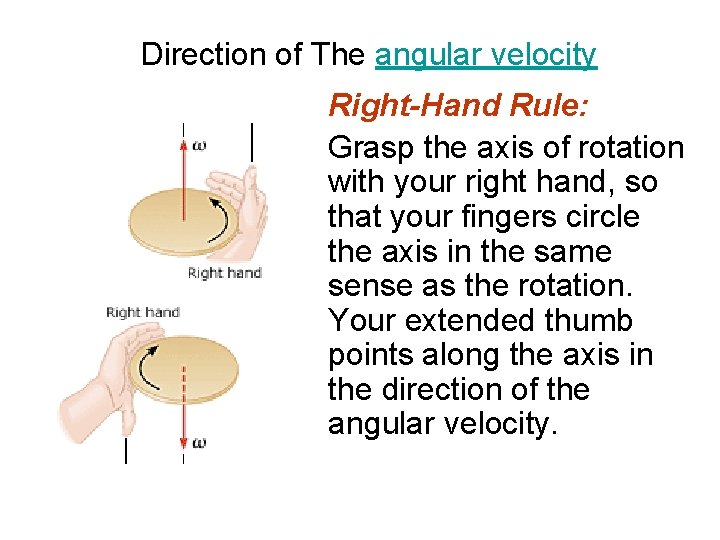
Direction of angular displacement Right-hand rule: Curl the fingers of your right hand in the direction of the rotation. • If your extended thumb points in the negative direction along the chosen axis of rotation, we call the rotational displacement negative. • If your thumb points in the positive direction along the axis of rotation, the rotational displacement was positive.
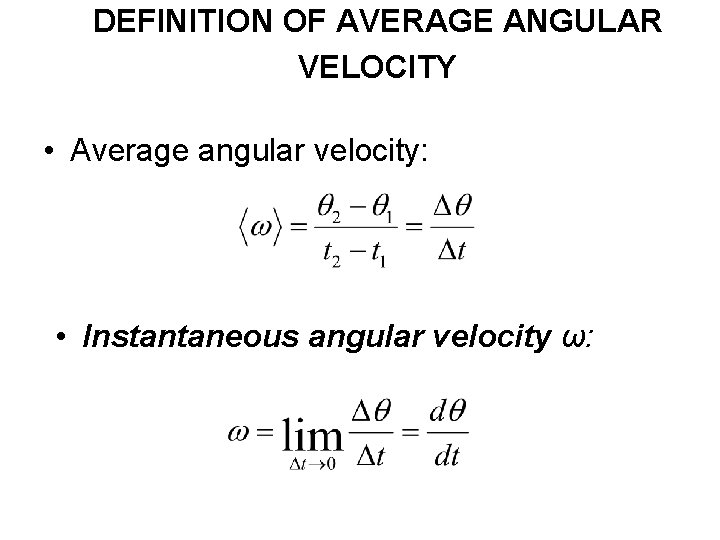
DEFINITION OF AVERAGE ANGULAR VELOCITY • Average angular velocity: • Instantaneous angular velocity ω:

Direction of The angular velocity Right-Hand Rule: Grasp the axis of rotation with your right hand, so that your fingers circle the axis in the same sense as the rotation. Your extended thumb points along the axis in the direction of the angular velocity.

DEFINITION OF ANGULAR ACCELERATION Average angular acceleration: Instantaneous angular acceleration: SI Unit of Average Angular Acceleration: radian per second squared (rad/s 2)

Direction of The angular acceleration The acceleration is a vector pointing along the axis of rotation. The acceleration vector has the same direction as the change in the angular velocity: • When the angular velocity is increasing, the angular acceleration vector points in the same direction as the angular velocity. • When the angular velocity is decreasing, the angular acceleration vector points in the direction opposite to the angular velocity.

Example 1 A Jet Revving Its Engines A jet awaiting clearance for takeoff is momentarily stopped on the runway. As seen from the front of one engine, the fan blades are rotating with an angular velocity of – 110 rad/s, where the negative sign indicates a clockwise rotation (see Figure). As the plane takes off, the angular velocity of the blades reaches – 330 rad/s in a time of 14 s. Find the angular acceleration, assuming it to be constant.

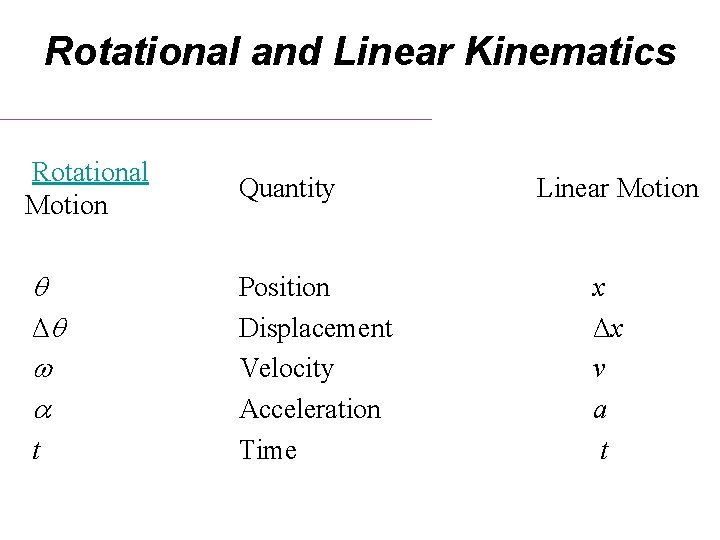
Rotational and Linear Kinematics Rotational Motion Quantity Linear Motion q Δq w a t Position Displacement Velocity Acceleration Time x Δx v a t

Rotation with Constant Rotational Acceleration Linear Motion Rotational Motion

Example 2 Blending with a Blender The blades of an electric blender are whirling with an angular velocity of +375 rad/s while the “puree” button is pushed in, as Figure 8. 11 shows. When the “blend” button is pressed, the blades accelerate and reach a greater angular velocity after the blades have rotated through an angular displacement of +44. 0 rad (seven revolutions). The angular acceleration has a constant value of +1740 rad/s 2. Find the final angular velocity of the blades.

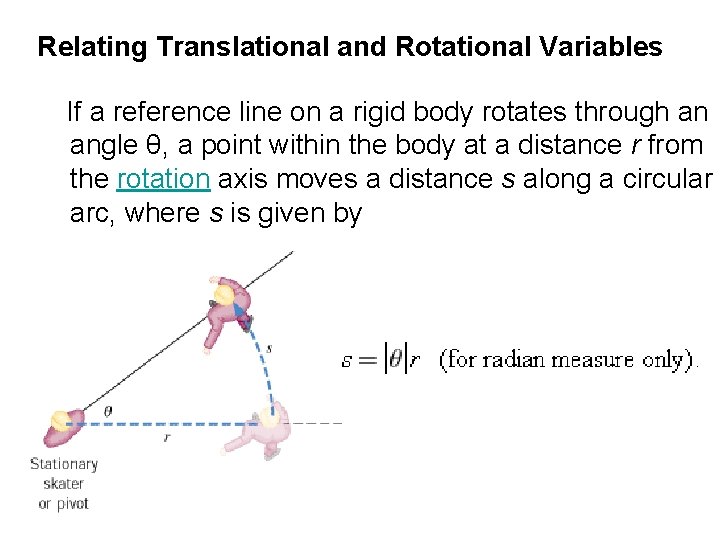
Relating Translational and Rotational Variables If a reference line on a rigid body rotates through an angle θ, a point within the body at a distance r from the rotation axis moves a distance s along a circular arc, where s is given by

Relating Rotational and Translational Speed • The rotational speed ω is the same at any points • The translational speed is different for the points with different distance from the rotational axis.

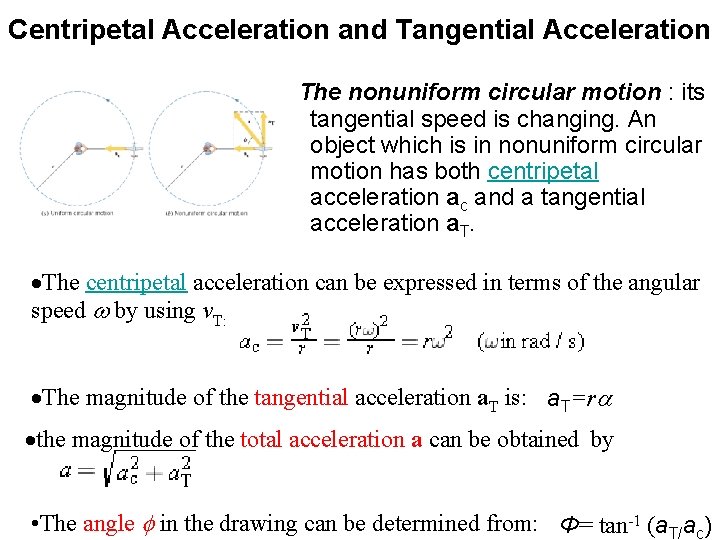
Centripetal Acceleration and Tangential Acceleration The nonuniform circular motion : its tangential speed is changing. An object which is in nonuniform circular motion has both centripetal acceleration ac and a tangential acceleration a. T. The centripetal acceleration can be expressed in terms of the angular speed w by using v. T: The magnitude of the tangential acceleration a. T is: a. T=ra the magnitude of the total acceleration a can be obtained by • The angle f in the drawing can be determined from: Φ= tan-1 (a. T/ac)

Example 3 A Helicopter Blade A helicopter blade has an angular speed of w=6. 50 rev/s and an angular acceleration of a=1. 30 rev/s 2. For points 1 and 2 on the blade in Figure, find the magnitudes of (a) the tangential speeds and (b) the tangential accelerations.

Example 4 A Discus Thrower Discus throwers often warm up by standing with both feet flat on the ground and throwing the discus with a twisting motion of their bodies. Figure (a) illustrates a top view of such a warm-up throw. Starting from rest, the thrower accelerates the discus to a final angular velocity of +15. 0 rad/s in a time of 0. 270 s before releasing it. During the acceleration, the discus moves on a circular arc of radius 0. 810 m. Find (a) the magnitude a of the total acceleration of the discus just before it is released and (b) the angle Φ that the total acceleration makes with the radius at this moment.

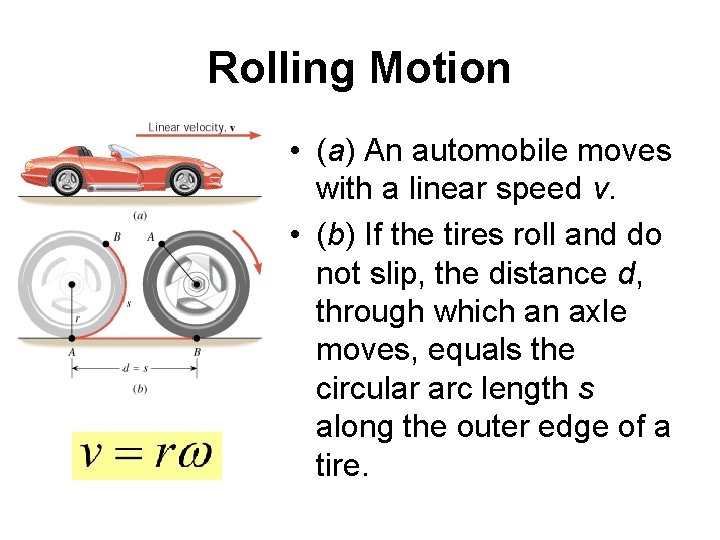
Rolling Motion • (a) An automobile moves with a linear speed v. • (b) If the tires roll and do not slip, the distance d, through which an axle moves, equals the circular arc length s along the outer edge of a tire.

Kinetic Energy of Rotation • The kinetic energy of a rigid rotating body is sum over kinetic energy all the particles in the body • Because v =ω r and ω is the same for all particles in a rigid rotating body, so that we have: • The rotational inertia for a collection of particles is defined as:

DEFINITION OF ROTATIONAL KINETIC ENERGY The rotational kinetic energy KER of a rigid object rotating with an angular speed ω about a fixed axis and having a rotational of inertia I is Requirement: ω must be expressed in rad/s. SI Unit of Rotational Kinetic Energy: joule (J)

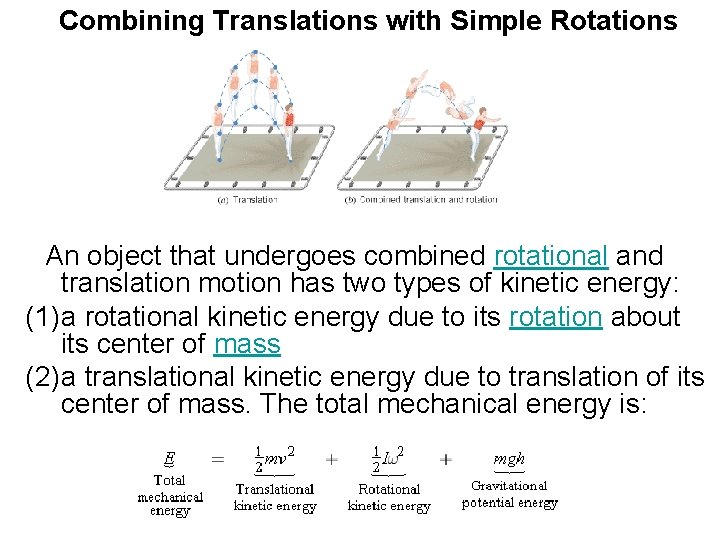
Combining Translations with Simple Rotations An object that undergoes combined rotational and translation motion has two types of kinetic energy: (1) a rotational kinetic energy due to its rotation about its center of mass (2) a translational kinetic energy due to translation of its center of mass. The total mechanical energy is:

Calculating Rotational Inertia For a continuous body, we define the rotational inertia of the body as

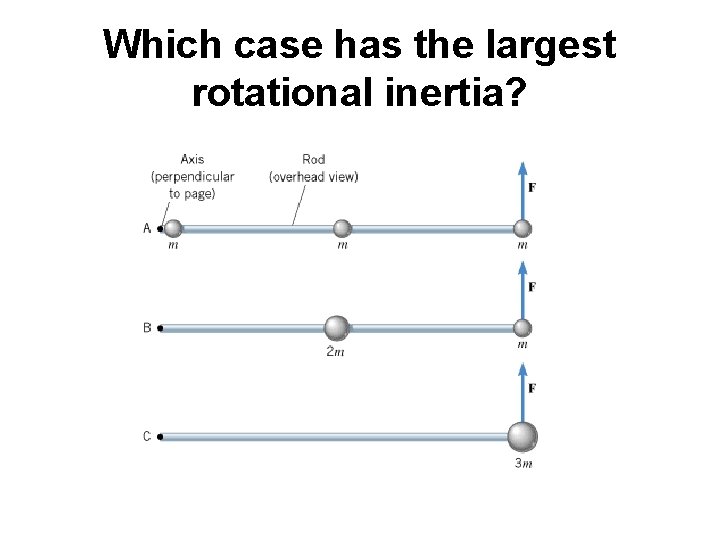
Which case has the largest rotational inertia?

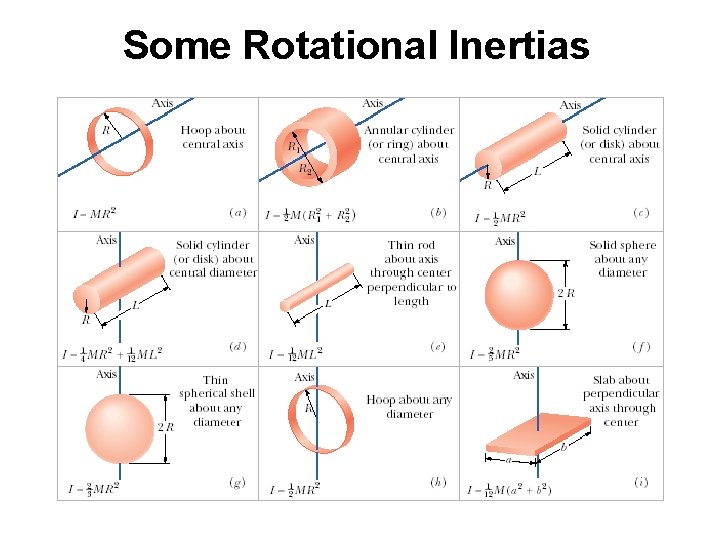
Some Rotational Inertias

Parallel-Axis Theorem If we know the rotational inertia of a symmetric object rotating about an axis passing through its center of mass, then the rotational inertia I about another parallel axis (where the perpendicular distance between the given axis and the axis through the center of mass is h) is:

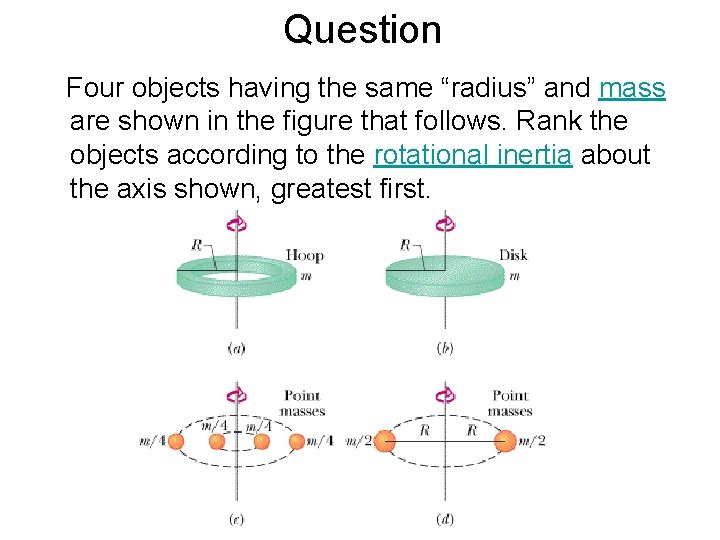
Question Four objects having the same “radius” and mass are shown in the figure that follows. Rank the objects according to the rotational inertia about the axis shown, greatest first.

Example 5 Rolling Cylinders A thin-walled hollow cylinder (mass=mh, radius=rh) and a solid cylinder (mass=ms, radius=rs) start from rest at the top of an incline (Figure). Both cylinders start at the same vertical height h 0. All heights are measured relative to an arbitrarily chosen zero level that passes through the center of mass of a cylinder when it is at the bottom of the incline (see the drawing). Ignoring energy losses due to retarding forces, determine which cylinder has the greatest translational speed upon reaching the bottom.

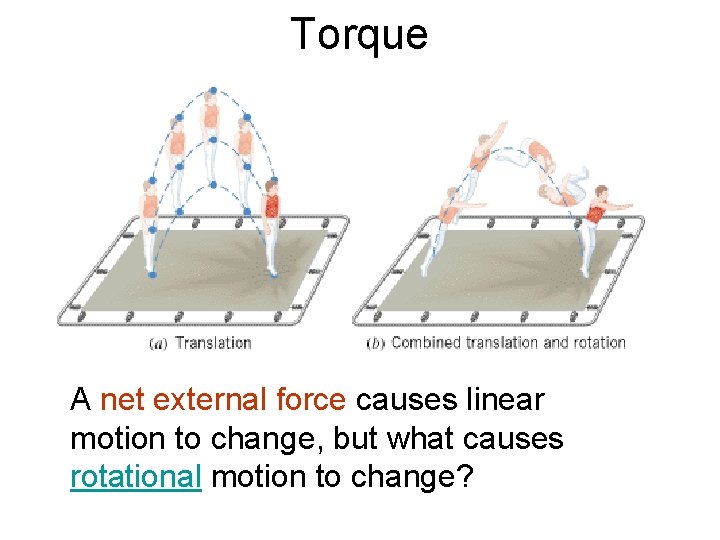
Torque A net external force causes linear motion to change, but what causes rotational motion to change?

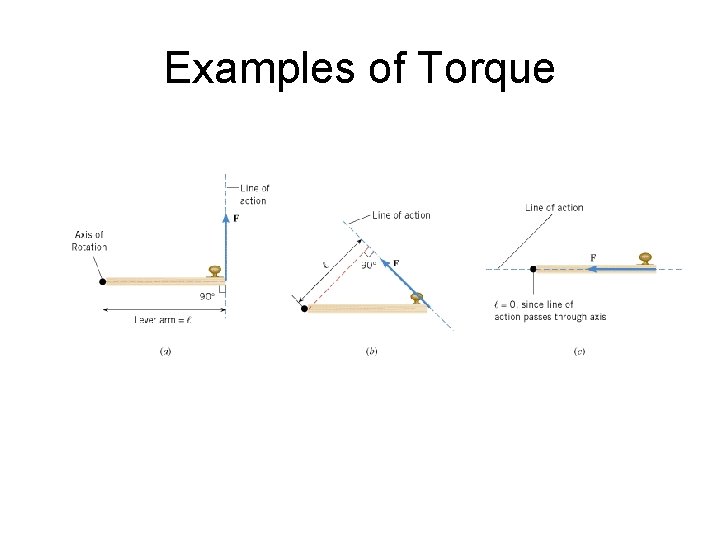
Examples of Torque

Definition of torque • Magnitude: • Direction is determined by the right hand rule. Note: for fixed rotational axis motion, only components of and in the x-y plane will contribute to the torque along the rotational axis

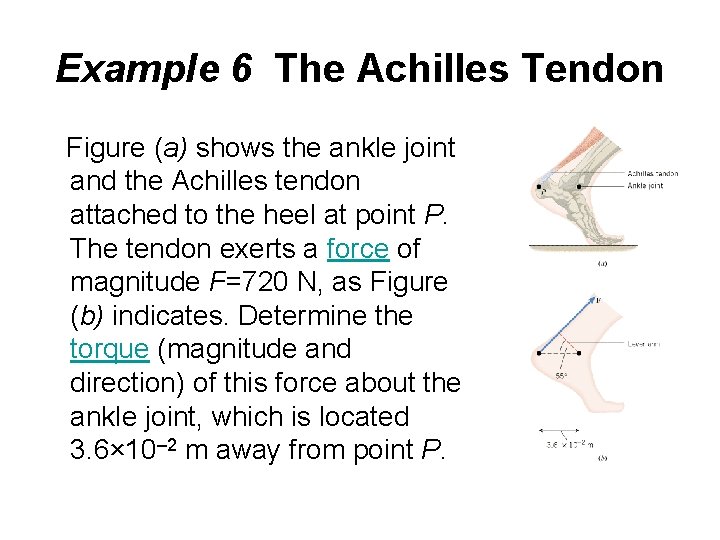
Example 6 The Achilles Tendon Figure (a) shows the ankle joint and the Achilles tendon attached to the heel at point P. The tendon exerts a force of magnitude F=720 N, as Figure (b) indicates. Determine the torque (magnitude and direction) of this force about the ankle joint, which is located 3. 6× 10– 2 m away from point P.

Newton's Second Law for Rotation ROTATIONAL ANALOG OF NEWTON’S SECOND LAW FOR A RIGID BODY ROTATING ABOUT A FIXED AXIS: Requirement: a must be expressed in rad/s 2. Important: and are vector components along the same axis

Example 7 The Torque of an Electric Saw Motor The motor in an electric saw brings the circular blade from rest up to the rated angular velocity of 80. 0 rev/s in 240. 0 rev. One type of blade has a moment of inertia of 1. 41× 10– 2 kg · m 2. What net torque (assumed constant) must the motor apply to the blade?

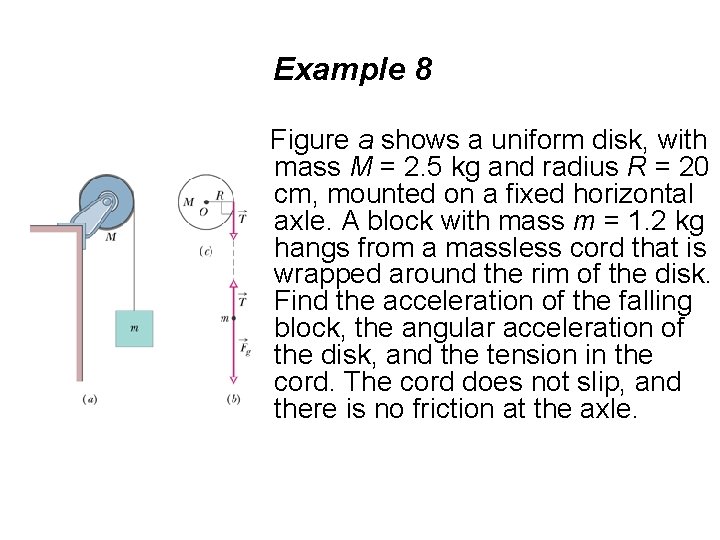
Example 8 Figure a shows a uniform disk, with mass M = 2. 5 kg and radius R = 20 cm, mounted on a fixed horizontal axle. A block with mass m = 1. 2 kg hangs from a massless cord that is wrapped around the rim of the disk. Find the acceleration of the falling block, the angular acceleration of the disk, and the tension in the cord. The cord does not slip, and there is no friction at the axle.

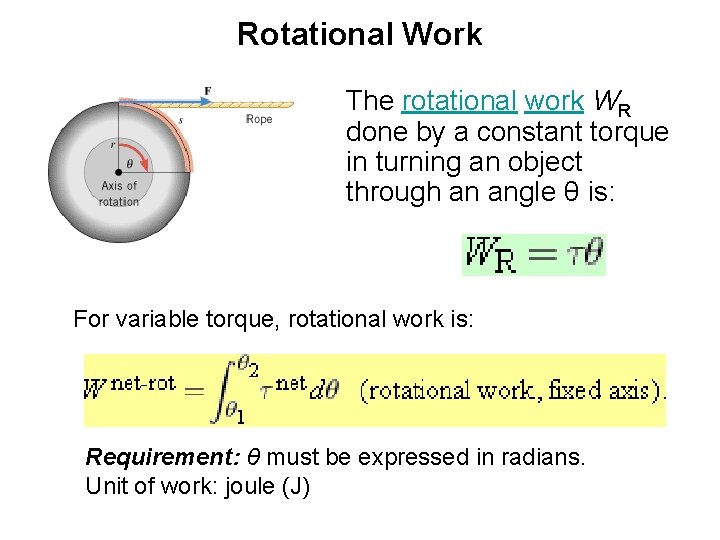
Rotational Work The rotational work WR done by a constant torque in turning an object through an angle θ is: For variable torque, rotational work is: Requirement: θ must be expressed in radians. Unit of work: joule (J)

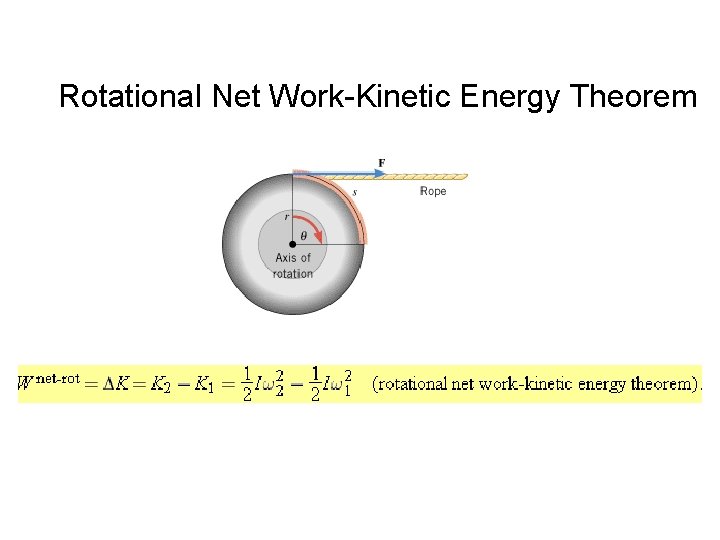
Rotational Net Work-Kinetic Energy Theorem

Power for a Rotating Body In addition, we can find the power P associated with the rotational motion of a rigid object about a fixed axis using the equation d. W = d : Note: The signs of both torque and rotational velocity are determined by the right-hand rule.

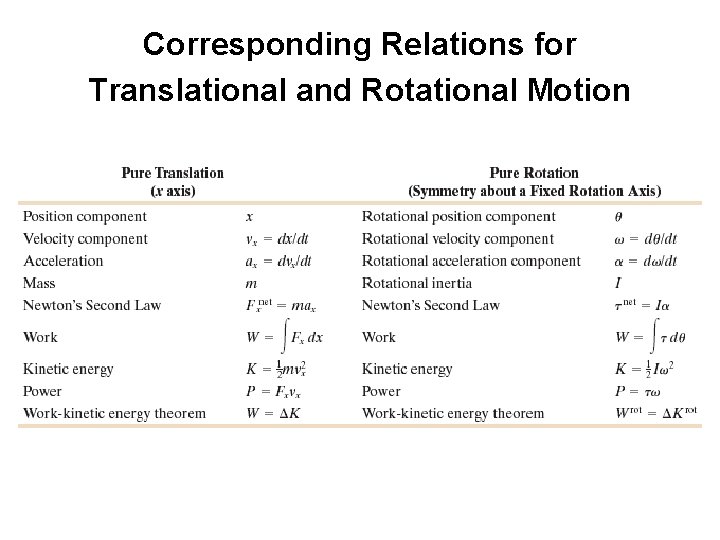
Corresponding Relations for Translational and Rotational Motion

EXAMPLE 9: Rotating Sculpture A rigid sculpture consists of a thin hoop (of mass m and radius R = 0. 15 m) and a thin radial rod (of mass m and length L = 2. 0 R), arranged as shown in Fig. The sculpture can pivot around a horizontal axis in the plane of the hoop, passing through its center. (a) In terms of m and R, what is the sculpture's rotational inertia I about the rotation axis? (b) Starting from rest, the sculpture rotates around the rotation axis from the initial upright orientation of Fig. What is its rotational speed ω about the axis when it is inverted?

Sample Problem 10 A tall, cylindrical chimney will fall over when its base is ruptured. Treat the chimney as a thin rod of length L = 55. 0 m (Fig. 10 -20 a). At the instant it makes an angle of θ=35 o with the vertical, what is its angular speed ωf ?

Conceptual Questions • 1 The earth rotates once per day about its axis. Where on the earth’s surface should you stand in order to have the smallest possible tangential speed? Justify your answer. • 2 Explain (a) how it is possible for a large force to produce only a small, or even zero, torque, and (b) how it is possible for a small force to produce a large torque.

• 3 A bicycle is turned upside down, the front wheel is spinning (see the drawing), and there is an angular acceleration. At the instant shown, there are six points on the wheel that have arrows associated with them. Which of the following quantities could the arrows represent: (a) tangential velocity, (b) tangential acceleration, (c) centripetal acceleration? In each case, answer why the arrows do or do not represent the quantity. • 4 An object has an angular velocity. It also has an angular acceleration due to torques that are present. Therefore, the an-gular velocity is changing. What happens to the angular velocity if (a) additional torques are applied so as to make the net torque suddenly equal to zero and (b) all the torques are suddenly removed?

• 5 The space probe in the drawing is initially moving with a constant translational velocity and zero angular velocity. (a) When the two engines are fired, each generating a thrust of magnitude T, will the translational velocity increase, decrease, or remain the same? Why? (b) Explain what will happen to the angular velocity. • 6 For purposes of computing the translational kinetic energy of a rigid body, its mass can be considered as concentrated at the center of mass. If one wishes to compute the body’s moment of inertia, can the mass be considered as concentrated at the center of mass? If not, why not?