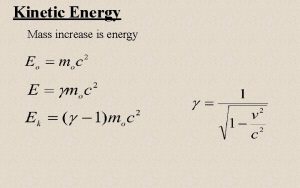The Race Rotational Kinetic Energy The Forgotten Kinetic
















- Slides: 23

The Race

Rotational Kinetic Energy The Forgotten Kinetic Energy

ENERGY l What is Energy? l The l ability of an object to do work. What are the two Forms of Energy? l Potential Energy l Kinetic Energy

KINETIC ENERGY l Translational Kinetic Energy l Rotational Kinetic Energy l Vibrational Kinetic Energy

CONSERVATION OF ENERGY “The law of conservation of energy states that the total amount of energy in an isolated system remains constant. A consequence of this law is that energy cannot be created or destroyed. ”

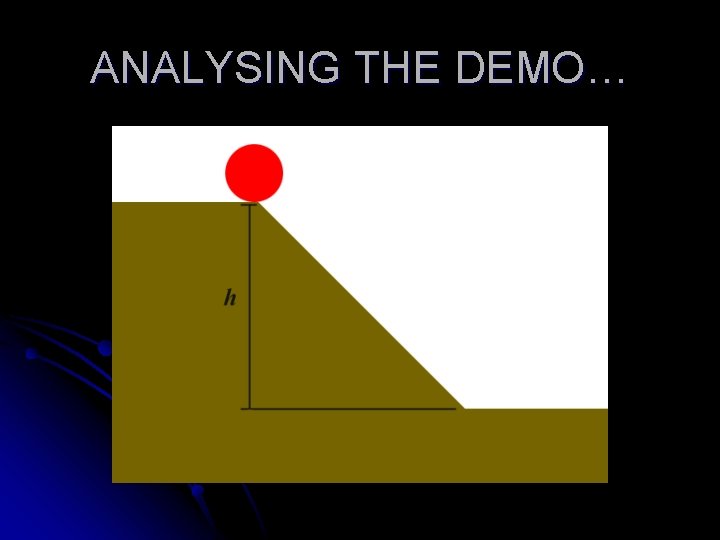
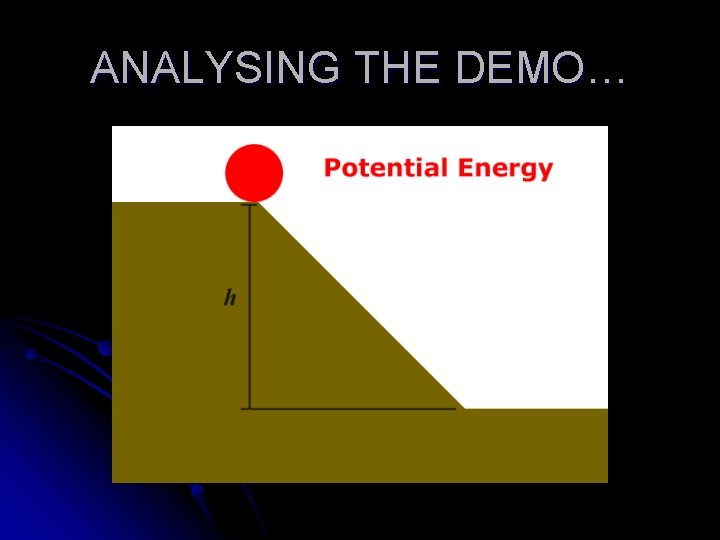
ANALYSING THE DEMO…

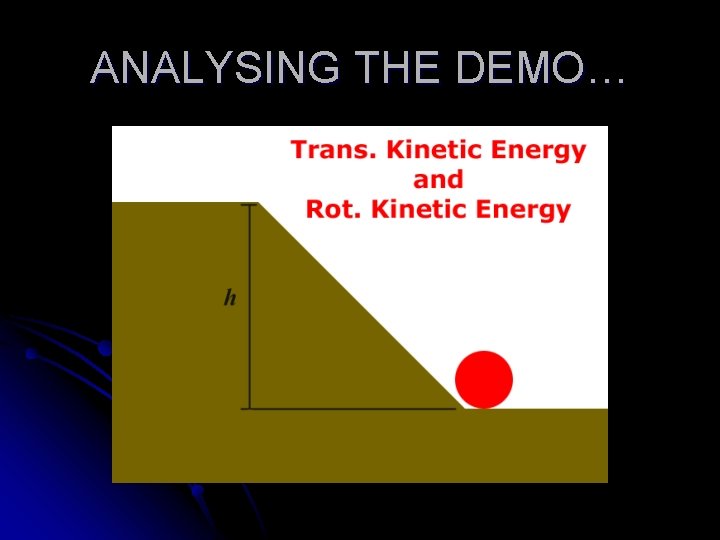
ANALYSING THE DEMO…

ANALYSING THE DEMO…

ANALYSING THE DEMO…

EQUATION REPRESENTATION

MOMENT OF INERTIA l What is Inertia? l l An object’s tendency to remain in whatever state it is in. Moment of Inertia l l A measure of an object’s resistance to rotational motion. Analogous to Mass l Mass dictates the degree of Translational Inertia; Moment of Inertia dictates the degree of Rotational Inertia.

MOMENT OF INERTIA l Depending on the axis of rotation, different objects have different moments of inertia.

Tangential Velocity B 1 > A 1 B 2 > A 2

EQUATION REPRESENTATION

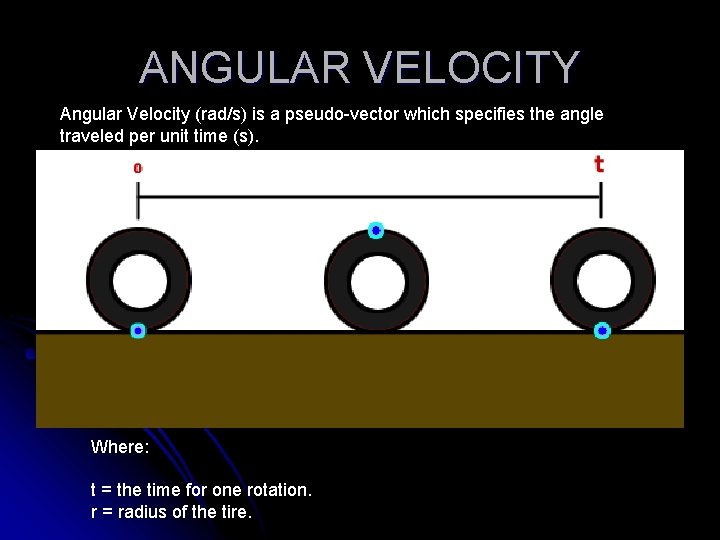
ANGULAR VELOCITY Angular Velocity (rad/s) is a pseudo-vector which specifies the angle traveled per unit time (s). Where: t = the time for one rotation. r = radius of the tire.

ANGULAR VELOCITY Where: • 2π = one rotation in radians • v = translational velocity • t = time for one rotation • r = radius of tire

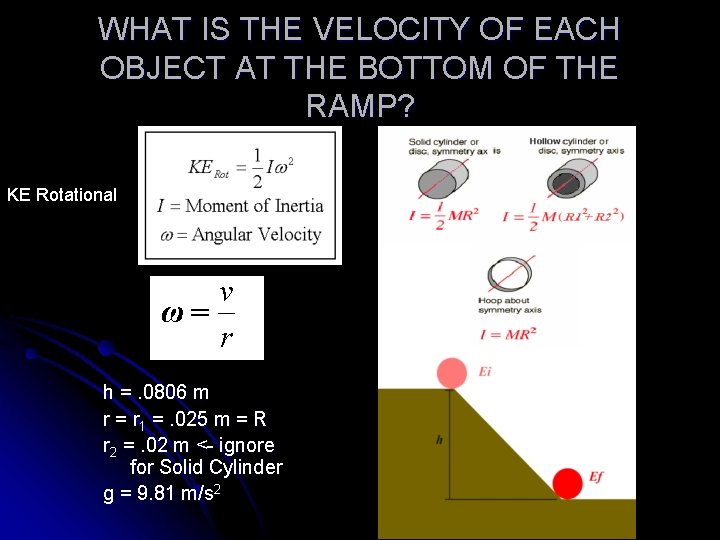
WHAT IS THE VELOCITY OF EACH OBJECT AT THE BOTTOM OF THE RAMP? KE Rotational h =. 0806 m r = r 1 =. 025 m = R r 2 =. 02 m <- ignore for Solid Cylinder g = 9. 81 m/s 2

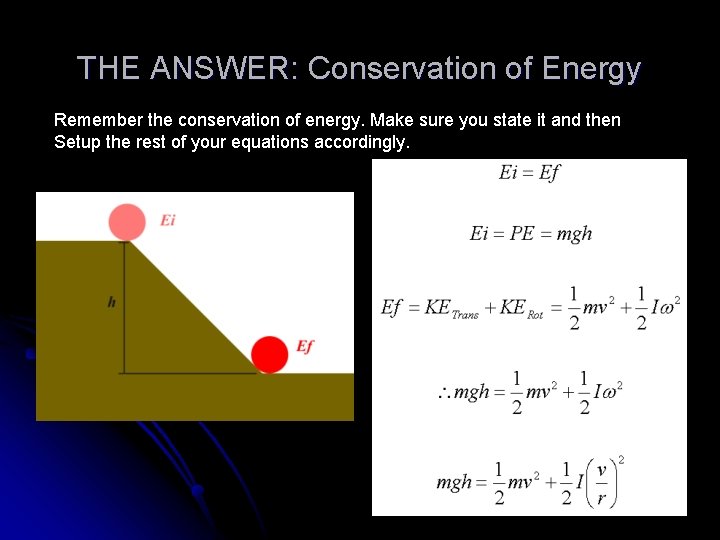
THE ANSWER: Conservation of Energy Remember the conservation of energy. Make sure you state it and then Setup the rest of your equations accordingly.

THE ANSWER: Rotational Kinetic Energy Use the Moment of Inertia from the list and the Angular Velocity in terms of Translational Velocity to find the Rotational Kinetic Energy.

THE ANSWER: Velocity! The masses cancel and you can easily solve for velocity. Velocity of Solid Cylinder: 1. 03 m/s Velocity of Hollow Cylinder: 0. 932 m/s Velocy of Hoop: 0. 889 m/s

THEORY vs PRACTICE l Do our theoretical values match up with our measured values? l If not, are they within reason? l What are some reasons they are different? l l l Friction A digital Camera is not very accurate. Location might not be exactly 8 cm off the table

CONCEPTUAL QUESTIONS l If they were to roll up an incline right after, what height would they stop at? l What would the velocity of the objects be if the ramp were frictionless?

QUESTIONS?
 Moment of inertia of disc
Moment of inertia of disc Kinetic rotational energy formula
Kinetic rotational energy formula Parallel axis theorem ap physics c
Parallel axis theorem ap physics c A rigid sculpture consists of a thin hoop
A rigid sculpture consists of a thin hoop Rotational kinetic energy
Rotational kinetic energy Rotational equilibrium and dynamics
Rotational equilibrium and dynamics Second condition of equilibrium
Second condition of equilibrium Data race vs race condition
Data race vs race condition Velocity triangle of pelton turbine
Velocity triangle of pelton turbine Dam
Dam Potential energy in spring
Potential energy in spring Gravity
Gravity Gravitational potential energy vs kinetic energy
Gravitational potential energy vs kinetic energy Kinetic energy to thermal energy
Kinetic energy to thermal energy Potential energy vs kinetic energy
Potential energy vs kinetic energy Where is the highest potential energy
Where is the highest potential energy Potential energy of a spring at equilibrium
Potential energy of a spring at equilibrium Gravitational potential energy
Gravitational potential energy Kinetic energy and potential energy formula
Kinetic energy and potential energy formula Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis The resourceful citer example
The resourceful citer example The forgotten footnote example
The forgotten footnote example Listening the forgotten skill
Listening the forgotten skill