WORK POWER ENERGY COLLISIONS What is Work Work

WORK POWER ENERGY COLLISIONS

What is Work? Work Done by a Constant Force Dimensions and Units of Work Nature of Work Done by a Variable Force Conservative and Non-Conservative Forces

What is Work? Work is said to be done when a force applied on a body produces some displacement in it in any direction except in a direction perpendicular to the direction of the force. For example, when a person carrying a load moves on a horizontal road, he is not performing any work as distance moved is in a direction perpendicular to the force applied.

When a constant force F acting on a body produces a displacement s in the body, then work done by the force(W) is the dot product of force and displacement i. e. W = F. s If is smaller angle between F and s, then W = Fscos

When displacement is produced in the direction of application of force then = 0°. cos = cos 0° = 1 W = Fs Thus work done by a constant force is the product of force and displacement, when the two vectors F and s are in the same direction. Work is a scalar quantity i. e. it has magnitude only and no direction.

WORK DONE IN RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM F = i^Fx +^j Fy +^k Fz s =^i x +^j y +^kz W=F. s + k Fz ) ^. ( i x^+ j y^+ kz W = (^i Fx +^j Fy ^ ) W = x F x + y Fy + z Fz

DIMENSIONS OF WORK As work = force * distance W = (M 1 L 1 T-2) * L = [ M 1 L 2 T-2 ] UNITS OF WORK Joule Work done is said to be 1 joule, when a force of 1 newton moves a body actually through a distance of 1 metre in the direction of applied force.

Erg Work done is said to be 1 erg, when a force of 1 dyne moves a body actually through a distance of 1 cm in the direction of applied force. RELATION BETWEEN JOULE AND ERG As 1 joule =1 N * 1 m * cos 0° 1 J = 105 dyne * 102 cm * 1 1 joule = 107 erg

(1) Positive Work As W = F. s = Fscos when is acute (<90 °) , cos is positive. Hence work done is positive. Example – When a body falls freely under the action of gravity. (2) Negative Work

when is obtuse (>90 °) , cos is negative Hence work done is negative. Example – When brakes are applied on moving vehicle. (3) Zero Work When = 90 °, cos = cos 90 °= 0 Hence work done is zero. Example – When a coolie carrying some

Work Done by a Variable Force F(x) Work done in moving R to S = F * dx = Area of PQRS D Work done in moving x 1 to x 2 x. A = x 1 Fdx x 2 W= x 1 x 2 O A S R PQ Fdx = Area of ABCD Hence work done by a variable force is numerically equal to the force curve and the displacement axis. C x. B B x

Power – It is defined as the rate at which the body can do the work, i. e. Power = Rate of doing work = Work / Time =W/t = ( F. s )/ t P = F. v Instantaneous Power – Power at a particular instant of time. P = dw / dt

DIMENSIONS OF POWER P = W/t = [M 1 L 2 T-2] / [T 1] = [M 1 L 2 T-3] UNITS OF POWER The SI unit of power is watt. From P= W/t, 1 Watt = 1 joule / 1 sec i, e 1 W = 1 Js-1

Hence power of an agent is said to be one watt, if it can do one joule of work in 1 second. Bigger units of power are – 1 kilo watt = 1000 watt 1 k. W = 103 1 mega watt = 1, 000 watt i. e. 1 MW = 106 W Absolute unit of power in c. g. s. system is 1 erg s-1 Another popular unit of power is horse power(h. p). 1 h. p = 746 W

Conservative and Non-Conservative Forces Conservative forces – If the amount of work done aganist the force depends on initial and final position of body moved the force is called conservative forces. Examples : - Gravitational force, Magnetic force. Work done against force does not

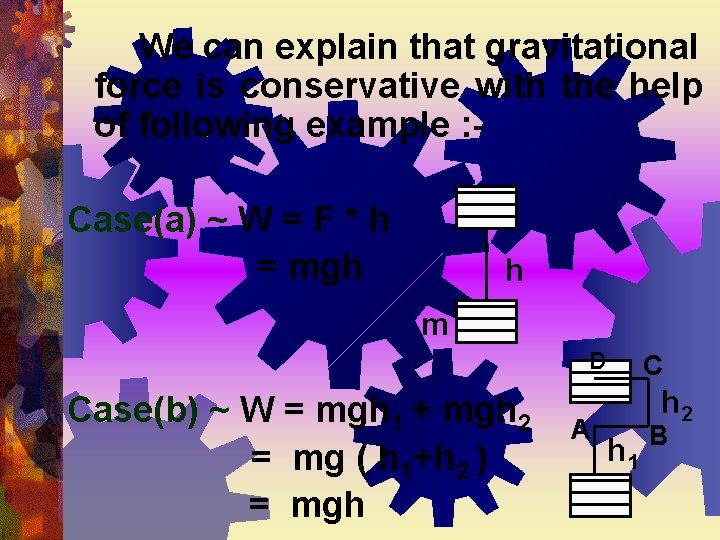
We can explain that gravitational force is conservative with the help of following example : Case(a) ~ W = F * h = mgh h m D Case(b) ~ W = mgh 1 + mgh 2 = mg ( h 1+h 2 ) = mgh A C h 2 h 1 B

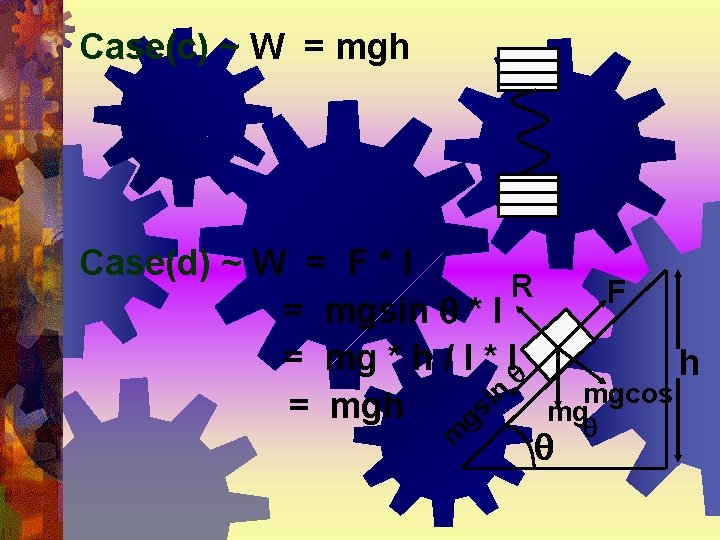
Case(c) ~ W = mgh Case(d) ~ W = F * l R = mgsin * l = mg * h / l * l n i = mgh gs m F mgcos mg h

Work done in lifting a body against gravity is independent of path taken only depends on initial and final position of the object. So, the gravitational force is conservative. Non-Conservative forces – If work done depend on the path taken by body in motion, the force is called nonconservative force. In this case, mechanical energy is not constant. Example : - frictional force depend on length of path.

What is Power? Dimensions and Units of Power

What is Energy? Types of Energy Different forms of Energy Work Energy Theorem Transformation of Energy Principle of Conservation of Energy

What is Energy? Energy of a body is defined as the capacity or ability of the body to do the work. DIMENSIONS OF ENERGY The dimensions of energy are [M 1 L 2 T-2]. UNIT OF ENERGY In SI, absolute unit of energy is joule and in c. g. s. system, the absolute unit of energy is erg.

TYPES OF ENERGY Energy is of several types e. g. mechanical energy, heat energy, light energy, electric energy, chemical energy, sound energy, nuclear energy, solar energy and so on. But we shall confine ourselves to the study of mechanical energy which is of two types : - KINETIC ENERGY POTENTIAL ENERGY

KINETIC ENERGY The kinetic energy of a body is the energy possessed by the body by virtue of its motion. For example: - A bullet fired from gun. EXPRESSION FOR KINETIC ENERGY From v 2 – u 2 = 2 as As u = 0 v 2 = 2 as a = v 2 / 2 s. . . . (1)

As , From (1) , F = ma F = m( v 2 / 2 s) Work done = Force * Distance W = mv 2 / 2 s * s W = ½mv 2 This work done on the body is a measure of kinetic energy of the body , K. E. of body = W = ½mv 2

POTENTIAL ENERGY The potential energy of a body is defined as the energy possessed by the body by virtue of its position. Example – A compressed spring. Three important types of potential energy are : Gravitational potential energy Elastic potential energy Electrostatic potential energy

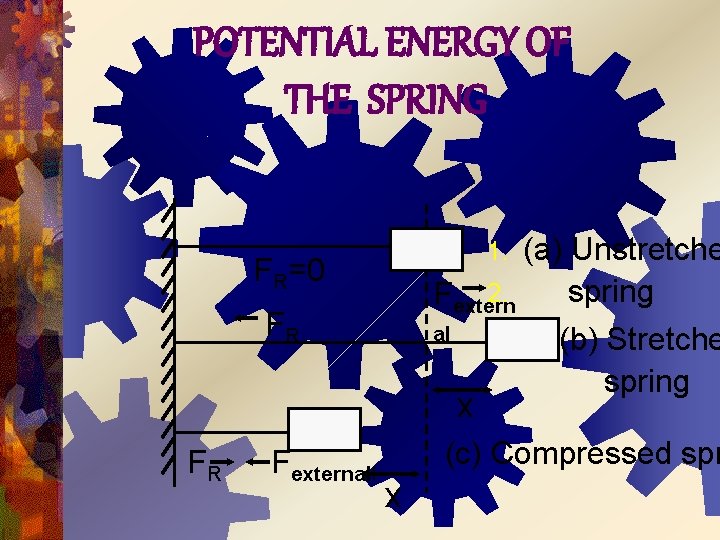
POTENTIAL ENERGY OF THE SPRING (a) Unstretche 2. spring Fextern al (b) Stretche spring 1. FR=0 FR x FR Fexternall (c) Compressed spr x

Let us consider smooth mass m attached to a spring whose one end is rigidly fixed to a wall as shown in the figure. For a small stretch or compression, spring obeys Hook’s law, Restoring force stretch or compression -F x

During the elongation and compression of spring, some work is done and that work is stored in the spring as its potential energy. A Force B O x(extension) Work done = Area of AOB = ½. x. F = ½. x. kx W = kx 2 / 2

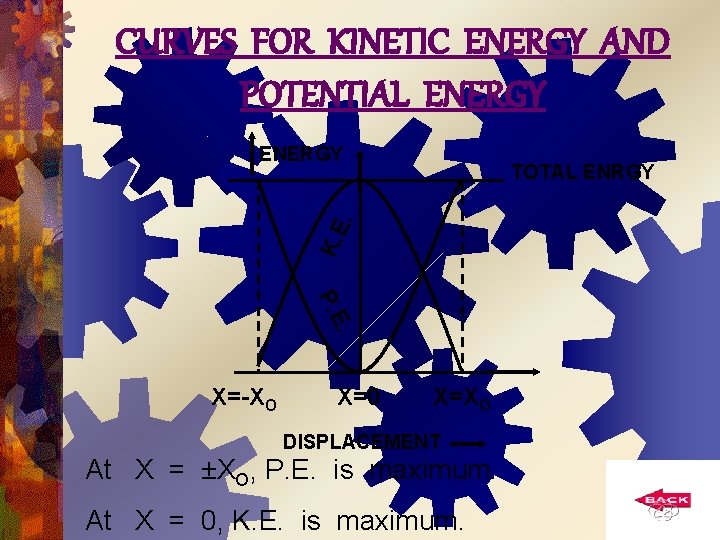
CURVES FOR KINETIC ENERGY AND POTENTIAL ENERGY K. E. TOTAL ENRGY . P. E X=-XO X=0 X=XO DISPLACEMENT At X = ±XO, P. E. is maximum. At X = 0, K. E. is maximum.

According this to principle, work done by a forces in displacing a body measures the changes in kinetic energy of the body. DERIVATION OF WORK ENERGY THEOREM Suppose , m = mass of the body, u = initial velocity of the body , F = force applied on the body in the direction of motion,

ds = small displacement of the body in the direction of F. d. W = F. ds = F ds cos 00 d. W = F ds = m a ds { F = ma } = m (dv / dt) ds { a = dv/dt } = m (ds / dt) dv dw = m v dv { v = ds/dt } Total work done by the force in increasing the body from u to v is W = mvdv = m [v 2/2]v = ½m(v 2 -u 2)

W W = ½mv 2 - ½mu 2 = Final K. E - Initial K. E = change in K. E of the body Hence work done by a force is a measure of change in K. E of a body, which proves the work energy principle.

Transformation of Energy It is a phenomenon of energy from one form to other. We come across such changes in day –to - day life. For example : - In an electric bulb, electric energy is converted into light energy and heat energy. In an electric iron , electric heater , geyser etc. , electric energy is converted into heat energy

In an electric fan , electric motor, electric energy is converted into mechanical energy. In a hydroelectric power station , potential energy of water is converted ultimately into electric energy. In a heat engine , chemical energy from coal / oil is converted into mechanical energy. In a nuclear reactor , mass is being converted into energy. In the sun and other stars , mass is being converted into energy , and so on.

Principle of Conservation of Energy

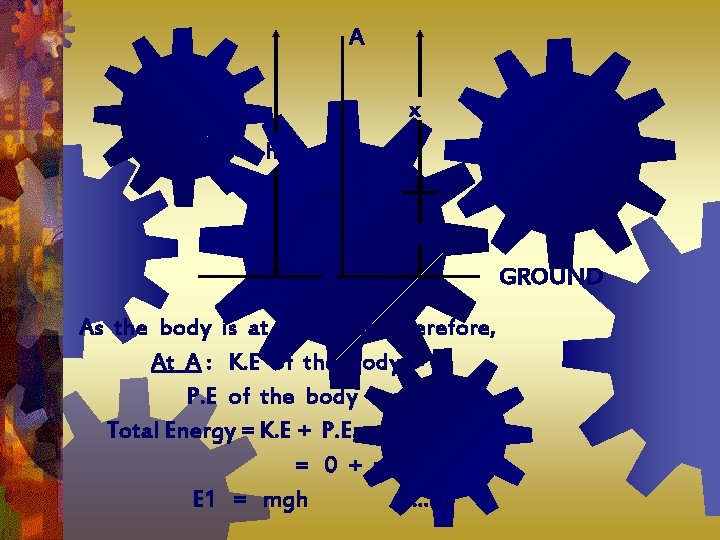
A x h B (h – x) C As the body is at rest at A , therefore, At A : K. E of the body = 0 P. E of the body = mgh, Total Energy = K. E + P. E. = 0 + mgh E 1 = mgh. . . (i) GROUND

Let the body be allowed to fall freely under gravity , when it strikes the ground at C with a velocity v. From v 2 - u 2 = 2 as v 2 – 0 = 2 gh v 2 = 2 gh. . . (ii) At C : K. E. of the body = ½ mv 2 = ½ m (2 gh) = mgh P. E. of the body = mgh = mg(0) = 0 Total energy of the body = K. E. + P. E E 2 = mgh + 0 = mgh. . . (iii)

In free fall, let the body cross any point B with a velocity v 1, where AB = x From v 2 –u 2 = 2 as v 12 - 0 = 2 gx v 12 = 2 gx . . . (iv) At B : K. E. of the body = 1/2 mv 12 = ½ m (2 gx) = mgx Height of the body at B above the ground CB = ( h – x ) =

P. E. of the body at B = mg(h - x ) Total energy of the body at B = K. E. + P. E. E 3 = mgx + mg ( h – x ) = mgx + mgh – mgx = mgh. . . . (v) From (i) , (iii) , (v) : E 1 = E 2 = E 3 = mgh

DIFFERENT FORMS OF ENERGY HEAT ENERGY : - It is the energy possessed by a body by virtue of random motion of the molecules of the body. INTERNAL ENERGY : - It is the energy possessed by the body of particular configuration of its molecules and also their random motion. ELECTRIC ENERGY : - It arises on account of work required to be done in

moving the free charge carriers in a particular direction through a conductor. CHEMICAL ENERGY : - chemical energy of a body , say a chemical compound is the energy possessed by it by virtue of chemical bonding of its atom. NUCLEAR ENERGY : - It is the energy obtainable from an atomic nucleus.

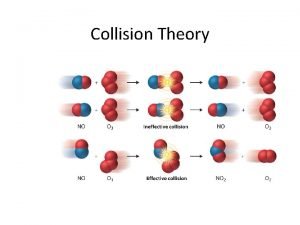
What is collision? Coefficient of Restitution Types of collision

WHAT IS COLLISION? A collision is defined as an isolated event in which two or more colliding bodies exert relatively strong forces on each other for a relatively short time.

Types of collision Collisions between particles have been divided broadly into two types : Elastic collisions Inelastic collisions

Elastic Collisions What is elastic collision? Elastic Collision in One Dimension Elastic Collision in Two Dimension

Elastic Collisions A collision in which there is absolutely no loss of kinetic energy is called an elastic collision. For example – Collision between atomic and sub atomic particles. CHARACTERISTICS OF AN ELASTIC COLLISION ARE : - The linear momentum is conserved.

The kinetic energy is conserved. The forces involved during elastic collisions must be conservative forces.

Inelastic collisions A collision in which there occurs some loss of kinetic energy is called an inelastic collision. For example - If a meteorite collides head on with earth, it becomes buried in earth. CHARACTERISTICS OF AN ELASTIC COLLISION ARE : - The linear momentum is conserved. Total energy of the system is

The kinetic energy is conserved. The forces involved during elastic collisions must be conservative forces.

Coefficient of Restitution It is defined as the ratio of relative velocity of separation after collision to the relative velocity of approach before collision. It relative velocity of sep e = is represented by ‘e’. relative velocity of ap

v 2 - v 1 e = u -u 1 2 where u 1 , u 2 are velocities of two bodies before collision and v 1 , v 2 are their respective velocities after collision. For a perfectly elastic

approach before collision. e=1 For a perfectly inelastic collision, relative velocity of separation after collision = 0. e =0 For all other collisions, e

Elastic Collision in One Dimension BEFORE COLLISION DURING COLLISION A m 1 u 1 B m 2 u 2 A B m 1 m 2 AFTER COLLISION A m 1 v 1 B m 2 v 2

Applying the law of conservation of momentum : Momentum before = Momentum after collision m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2. . (1) or m 1 ( u 1 – v 2 ) = m 2 ( v 2 – u 2 ). . . . (2) Applying the law of conservation of energy : Total K. E. of two = Total K. E. of two balls before collision balls after collision ½m 1 u 21 + ½ m 2 u 22 = ½ m 1 v 21 + ½ m 2 v 22. . (3)

or 2 2 m 1 ( u 1 – v 2 ) = 2 2 m 2 ( v 2 – u 2 ). . . (4) Dividing (4) by (2) , we get : 2 2 m 1 ( u 1 – v 2 ) = m 1 ( u 1 – v 2 ) u 1 + v 1 = u 1 – u 2 = m 2 ( v 2 – u 2 ) v 2 + u 2 v 2 – v 1. . . (5) Relative velocity of approach = of separation before collision after collision From (5), v 2 – v 1 = e = 1 u 1 – u 2

Calculation of velocities after collision : VELOCITY OF A : From (5), v 2 = u 1 + v 1 – u 2 Putting this value in (1) : m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2(u 1 + v 1 – u 2) m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 u 1 + m 2 v 1 – m 2 u 2 v 1 = ( m 1 u 1 + 2 m 2 u 2 - m 2 u 1 ) / ( m 1 + m 2 ). . (6) u 1 ( m 1 - m 2 ) + 2 m 2 u 2 v 1 = m 1 + m 2 VELOCITY OF B : Putting this value of v 1 in (5) : -

v 2 = u 1 – u 2 + u 1 ( m 1 - m 2 ) + 2 m 2 u 2 m 1 + m 2 v 2 = ( u 1 – u 2 ) ( m 1 - m 2 ) + u 1 ( m 1 - m 2 ) + 2 m 2 u 2 m 1 + m 2 v 2 = 2 m 1 u 1 + u 2 ( m 2 – m 1 ) . . (7) m 1 + m 2 1) When masses of two bodies are equal : m 1 = m 2 = m From (6), v 1 = 2 mu 2 / 2 m = u 2 i. e. velocity of A = velocity of B after collision before collision

From (7), v 2 = 2 mu 1 / 2 m = u 1 i. e. velocity of B = velocity of A after collision before collision Hence after collision , velocities are just interchanged. 2) When the target body B is initially at rest : i. e. u 2 = 0 From (6), v 1 = ( m 1 - m 2 ) u 1 / (m 1 + m 2). . (8) From (7), v 2 = 2 m 1 u 1 / (m 1 + m 2). . (9) THREE CASES ARISE FURTHER: (a) When masses of two bodies are equal : i. e. m 1 = m 2

From (8), From (9), v 1 = 0 v 2 = 2 m 1 u 1 / 2 m 1 = u 1 i. e. body A comes to rest and body B starts moving with the initial velocity of A. (b) When body B at rest is very heavy : i. e. m 2 >> m 1 can be ignored compared to m 2. Putting m 1 = 0 in (8) and (9) , we obtain : v 1 = - m 2 u 1 / m 2 = -u 1 v 2 = 0 Hence when a light body A collides against a heavy body B at rest then A rebounds with its own velocity and B continues to be at rest.

(c) When body B at rest has negligible mass : i. e. m 2 << m 1 m 2 can be ignored compared to m 1. Putting m 2 = 0 in (8) and (9) , we obtain : v 1 = m 1 u 1 / m 1 = u 1 v 2 = 2 m 1 u 1 / m 1 = 2 u 1 Hence when a heavy body A undergoes an elastic collision with a light body B at rest, the body A keeps on moving with the same velocity of its own and the body B starts moving with double the initial velocity of A.

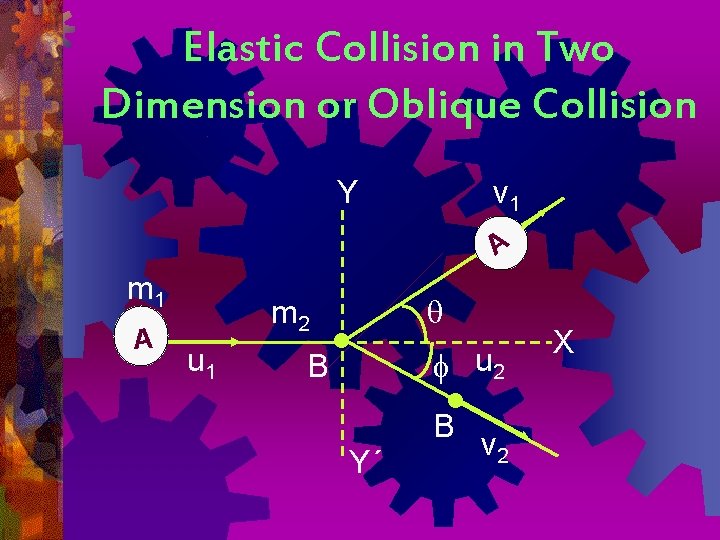
Elastic Collision in Two Dimension or Oblique Collision Y v 1 A m 2 u 1 • B Y´ u 2 • B v 2 X

As the collision is elastic, kinetic energy is conserved. Total K. E. after = Total K. E. before collision 2 2 or ½m 1 u 1 + ½ m 2 u 2 = ½ m 1 v 1 + ½ m 2 v 2. . . . (10) m 1 u 21 + m 2 u 22 = m 1 v 21 + m 2 v 22. . (11) As linear momentum is conserved in elastic collision, therefore, along X-axis, total linear momentum = total linear momentum after collision m 1 v 1 cos + m 2 v 2 cos = m 1 u 1 + m 2 u 2. . . . (12) Along Y-axis, m 1 v 1 sin - m 2 v 2 sin = 0. . . . (13)

From three equations (11), (12) and (13), we have to calculate four variables v 1, v 2, and , which is not possible. We have, therefore, to measure experimentally any one parameter.

MRS CHITRA JOSHI PGT (PHYSICS) KV FRI DEHRADUN