CHAPTER 4 WORK POWER AND ENERGY WORK DEFINITION

CHAPTER 4 WORK , POWER AND ENERGY

WORK

DEFINITION • Work involve force and displacement. • The work done by a constant force acting on a object is equal to the product of the magnitudes of the displacement and the component of the force parallel to that displacement.

Where F => force (N) d => displacement (m) W => work (Nm @ J) Θ => angle between displacement and force vectors WORK = an activity involving a force and movement in the direction of the force or when a force acts upon an object to cause a displacement of the object

• Work then involves a force acting on an object through distance. But if there is no motion (or no displacement), then no work is done. • For a constant force F acting in the same direction as the displacement, d , the work (W) done as. In this case work is a scalar quantity (may have +ve and –ve value). W =F d • In general, work is done on an object only by a force , or force component, parallel to the line of motion or displacement of the object.

• That is, if the force acts at an angle θ, to the object’s displacement, then F Cos θ is the component of force parallel to the displacement. In general work done by constant force W = (F Cos θ ) d • Note that the SI unit for work is Newtonmeter (N-m) or Joule (J). * 1 N-m = 1 J

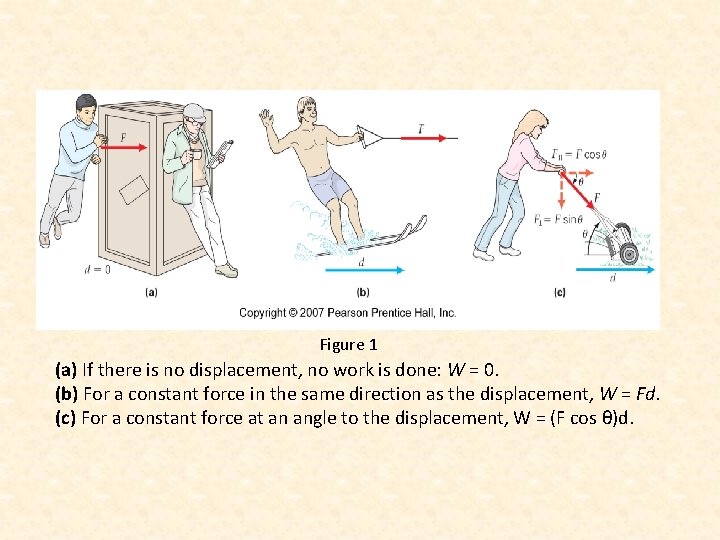
Figure 1 (a) If there is no displacement, no work is done: W = 0. (b) For a constant force in the same direction as the displacement, W = Fd. (c) For a constant force at an angle to the displacement, W = (F cos θ)d.

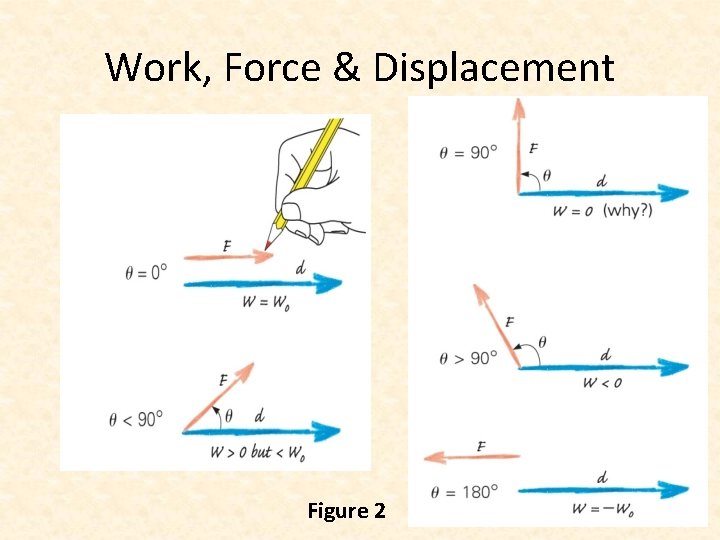
Work, Force & Displacement Figure 2

Total or Net work • Work done by all the forces acting on the object or scalar sum of all those quantities of work. • The concept of net force ### SCAN

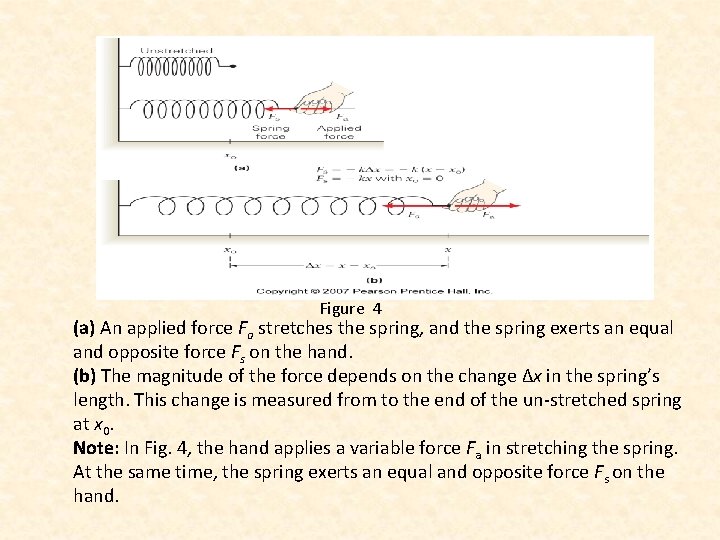
Work Done by a Variable Force • Forces in practice will often vary, they change in magnitude or angle with time or position. E. g. Someone might push harder and harder on an object to overcome the force of static friction, until the applied force exceeds fsmax. • For ideal spring force: • Thus, where k = force constant x= distance

Figure 4 (a) An applied force Fa stretches the spring, and the spring exerts an equal and opposite force Fs on the hand. (b) The magnitude of the force depends on the change Δx in the spring’s length. This change is measured from to the end of the un-stretched spring at x 0. Note: In Fig. 4, the hand applies a variable force Fa in stretching the spring. At the same time, the spring exerts an equal and opposite force Fs on the hand.

ENERGY

DEFINITION • The property of a system that enables its to do work or the ability to do work. When work is done, energy is transferred. • Units: Joules (J) • Source of energy – practically all our energy is the sun. • Form of energy - electrical, chemical heat, nuclear, mechanical , thermal, sound etc.

Types of Energy • 2 types of energy i) Kinetic Energy • Kinetic energy is energy of motion • Energy that a body possesses by virtue of being in motion. ii) Potential Energy • the energy possessed by a body by virtue of its position relative to others, stresses within itself, electric charge, and other factors.

Kinetic Energy Concept • Kinetic energy is the ability to do work through motion. Also called as energy of motion. Remember Multiply both side with mass; Thus, kinetic energy; K = kinetic energy m= mass v = velocity vf = final velocity vo = initial velocity

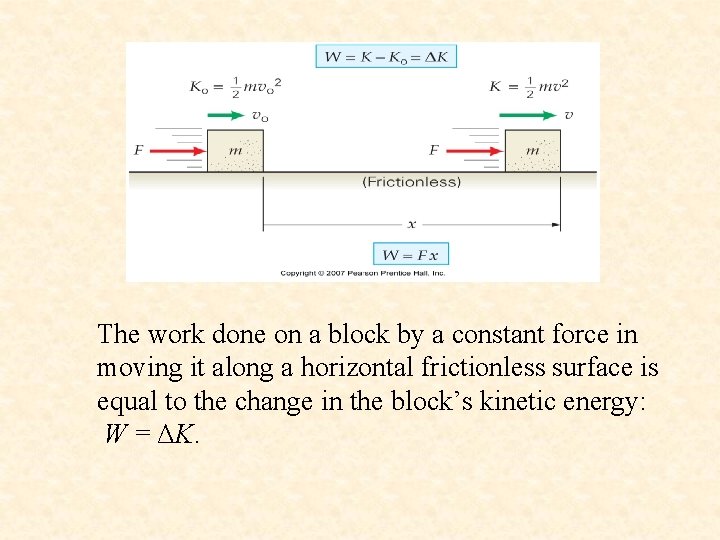
The work done on a block by a constant force in moving it along a horizontal frictionless surface is equal to the change in the block’s kinetic energy: W = ΔK.

Potential Energy • Potential energy exists whenever an object which has mass has a position within a force field (gravitational, magnetic, electrical). • An object having potential energy has potential to do work • Often called the energy of position • We will focus primarily on gravitational potential energy (energy an object has because of its height above the Earth)

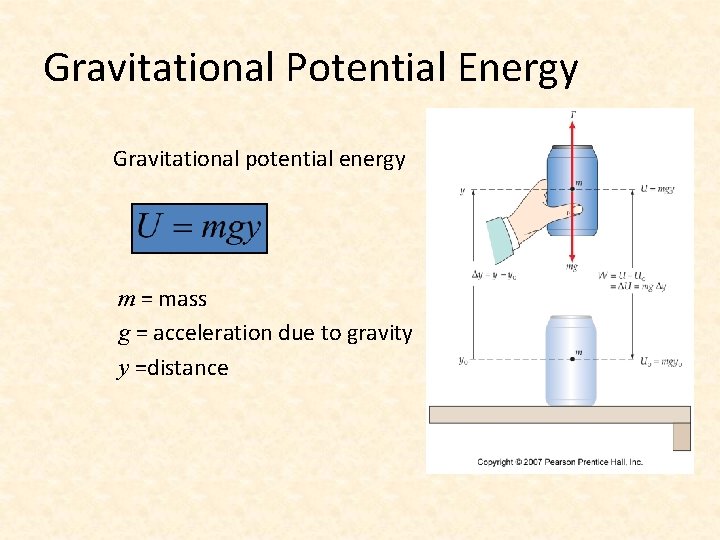
Gravitational Potential Energy Gravitational potential energy m = mass g = acceleration due to gravity y =distance

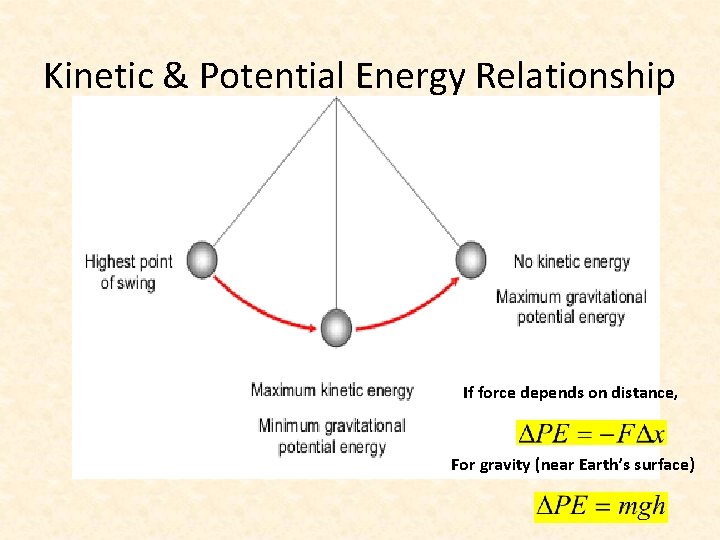
Kinetic & Potential Energy Relationship If force depends on distance, For gravity (near Earth’s surface)

The Law of Conservation of Energy • The Law of Conservation of Energy States: the total energy of an isolated system is always conserved • Energy is neither created nor destroyed; it is converted from one form to another • example in a nuclear power station. – Nuclear energy is converted into heat. – Heat boils water to steam – Heat in the steam is converted into kinetic energy in the turbines – Which is converted into electrical energy in the generator

Conservative & Non-conservative Force Conservative Non-conservative Work done by it in moving an object is independent of the object’s path Work done by it in moving an object does depend on the object’s path depends only on the initial and final positions of an object E. g: Friction, a longer path would produce more work done by friction than a shorter one, more energy would be lost Total energy is constant E = Eo, K + U = Ko - Uo Total energy is not constant E = Eo Allows to conserve or store energy as potential energy

Power

Definition • the rate of doing work or the rate of using energy • Power = energy transferred (J) time taken (s) = work done (J) time taken (s) • SI Unit : 1 W (watt) = 1 Js-1 (joule per second) • British Unit: 1 hp (Horsepower) = 746 W

• Work done = force x distance moved: W • Power = energy ÷ time: P = W/t • Speed = distance ÷ time: v = s/t • So we can write: P = W/t = Fs/t • Therefore: Power (W) = force (N) × speed (m/s) = Fs

Efficiency • Relates work output to energy (work) input as a percent ε = Work output Energy input ε = Power output Power input

Summary • Work done by a constant force is the product of magnitude of the displacement and the component of the force parallel to the displacement. • Calculating work done by variable force requires advance mathematics. An example of a variable force is the spring force, given by Hooke’s Law : Fs = - kx. • The work done by spring force is given by W= ½ kx 2

• Kinetic energy is the energy of motion an is given by • By the work-energy theorem, the net work done on an object is equal to the change in the kinetic energy of the object. O W = K – K = K • Potential Energy is the energy of position and/or configuration. The elastic potential energy of a spring is given by 2 U = ½ kx with x = 0

• The most common type of potential energy is gravitational potential energy, associated with the gravitational attraction near the Earth’s surface. U = mgy • Conservation of energy : the total energy of the universe or of an isolated system is always conserved. • Power : time rate of doing work or expanding energy. • Efficiency relates work output to energy (work) input as a percent (%).

EXERCISE

Q 1 A students holds a book, which has a mass of 1. 5 kg, out a second -story dormitory until her arm is tired, then she releases it (a) How much work is done on the book by the student in simply holding it out the window? (b) How much work is done by the force of gravity during the time in which the book falls 3. 0 m?

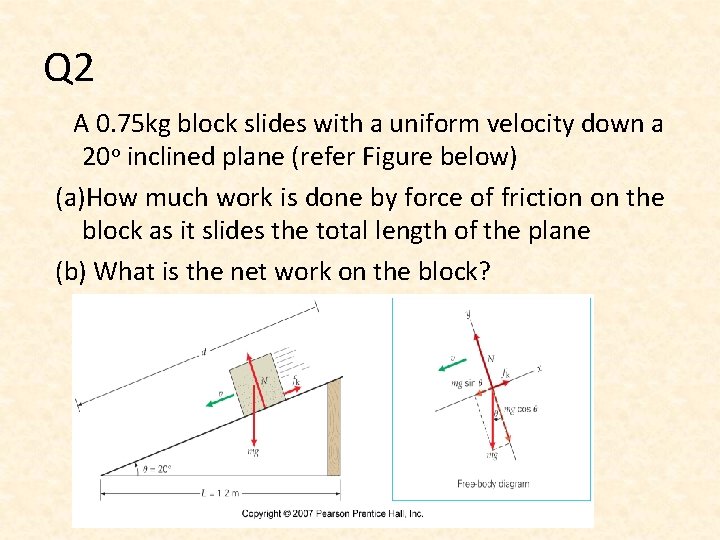
Q 2 A 0. 75 kg block slides with a uniform velocity down a 20 o inclined plane (refer Figure below) (a)How much work is done by force of friction on the block as it slides the total length of the plane (b) What is the net work on the block?

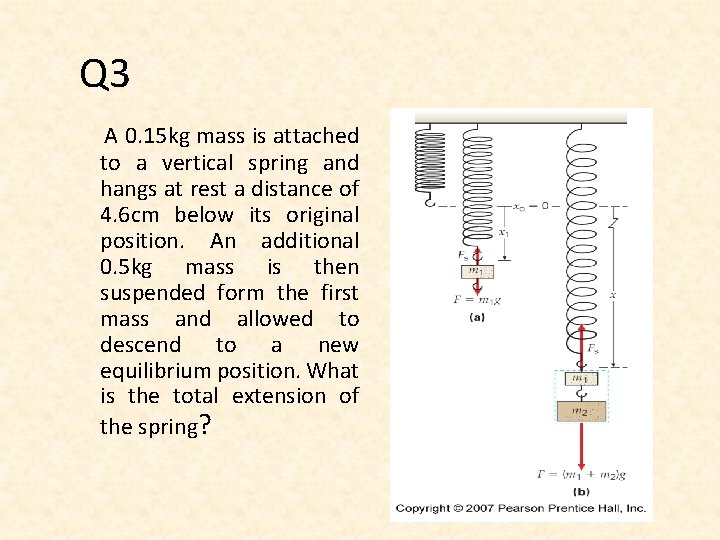
Q 3 A 0. 15 kg mass is attached to a vertical spring and hangs at rest a distance of 4. 6 cm below its original position. An additional 0. 5 kg mass is then suspended form the first mass and allowed to descend to a new equilibrium position. What is the total extension of the spring?

Q 4 Calculate the kinetic energy of a 4 kg shotput thrown by an athlete at a speed of 15 m/s? Q 5 Determine the potential energy of a 12 kg mass raised to a height of 25 m?