Weryfikacja hipotez parametrycznych WERYFIKACJA HIPOTEZ STATYSTYCZNYCH Przez hipotez

* Weryfikacja hipotez parametrycznych

WERYFIKACJA HIPOTEZ STATYSTYCZNYCH Przez hipotezę statystyczną rozumie się dowolne przypuszczenie na temat wartości parametrów lub postaci funkcyjnej zbiorowości generalnej. Z hipotezą parametryczną mamy do czynienia gdy przypuszczenie to dotyczy wartości parametrów rozkładu, natomiast pozostałe hipotezy nazywane są hipotezami nieparametrycznymi. W testach istotności hipotezę H 0 formułuje się jako hipotezę „o równości” natomiast hipotezę alternatywną H 1 jako hipotezę o „różności”, „większości” lub „mniejszości”.

Q - parametr zbiorowości generalnej oszacowany na podstawie próby, Q 0 – porównywana z nim wartość hipotetyczna. H 0: H 1 : Q = Q 0 Q ≠ Q 0 Q > Q 0 Q < Q 0 H 0: Q = Q 0 H 1: Q ≠ Q 0 H 0: Q ≤ Q 0 H 1: Q > Q 0 H 0: Q ≥ Q 0 H 1: Q < Q 0

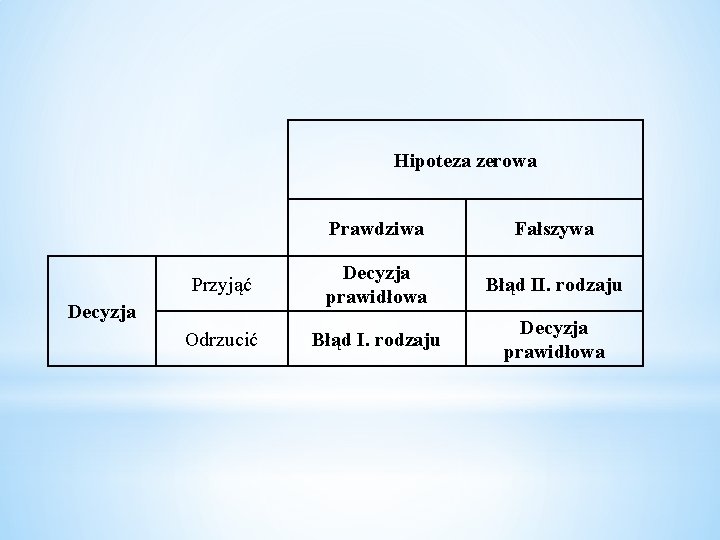
Hipoteza zerowa Prawdziwa Fałszywa Przyjąć Decyzja prawidłowa Błąd II. rodzaju Odrzucić Błąd I. rodzaju Decyzja prawidłowa Decyzja

Oznaczmy przez D pewną charakterystykę, która jest miarą odchylenia między rozkładem z próby a rozkładem hipotetycznym. Miara ta nazywa się zwykle sprawdzianem hipotezy i określa się ją jako funkcję wyników próby, na podstawie której podejmuje się decyzję przyjęcia lub odrzucenia hipotezy zerowej.

* Obszarem krytycznym, zwanym inaczej obszarem odrzuceń lub zbiorem krytycznym nazywamy podzbiór przestrzeni prób, który ma tę własność, że jeżeli wartość charakterystyki D zostanie zakwalifikowana do niego, to wtedy hipotezę zerową należy odrzucić.

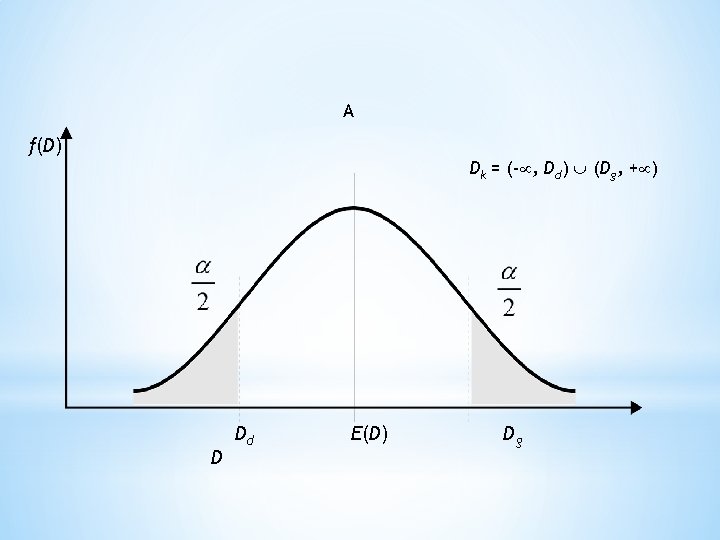
Obszar krytyczny zbudowany z dwóch rozłącznych przestrzeni prób w rozkładzie charakterystyki nosi nazwę obszaru krytycznego testu dwustronnego. Obszar krytyczny testu w zależności od hipotezy alternatywnej może być jednostronny, lewolub prawostronny. Test jest dwustronny w zależności od tego, czy odrzuca się hipotezę zerową dla wartości charakterystyki testu, która przypada na dwa przedziały lub tez na jeden przedział rozkładu z próby. *

Wprowadzenie podziału testów na jednostronny i dwustronny ma swoje uzasadnienie w przypadku odczytywania z tablic statystycznych wartości krytycznych Dα. Jeżeli, na przykład, sprawdzamy hipotezę stosując test jednostronny, a tablice statystyczne zbudowane dla testu dwustronnego, to wtedy Dα odczytujemy nie dla poziomu istotności α, ale dla podwojonego poziomu istotności, tzn. dla 2 α.

A f(D) Dk = (- , Dd) (Dg, + ) D Dd E(D) Dg

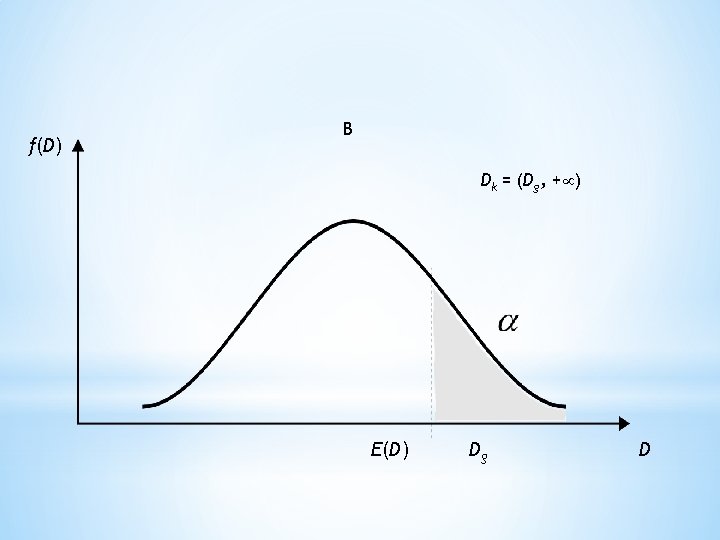
f(D) B Dk = (Dg, + ) E(D) Dg D

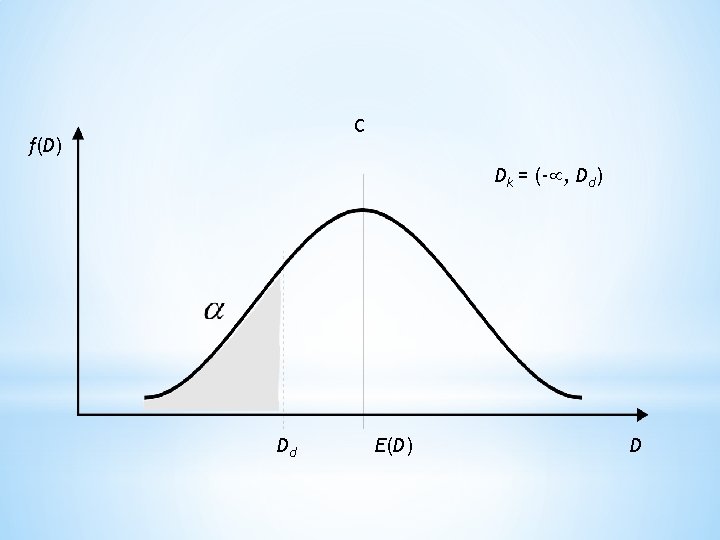
C f(D) Dk = (- , Dd) Dd E(D) D

Weryfikacja hipotez dotyczących wartości oczekiwanej Zmienna X w zbiorowości generalnej ma rozkład N(m, ) lub zbliżony do normalnego i wartość m jest nieznana: H 0: m=m 0 1) - znane H 1: m m 0 H 1: m>m 0 H 1: m<m 0 2) - nieznane, n>30 3) - nieznane, n 30 Statystyka t ma rozkład Studenta z n-1 stopniami swobody

Przyjmijmy, że zbiorowość generalna ma rozkład normalny N(m, σ ) o nieznanej wartości średniej. Ze zbiorowości tej wylosowano n-elementową próbę statystyczną w celu zweryfikowania hipotezy H 0, że wartość oczekiwana z próby równa jest wartości oczekiwanej zbiorowości. W tym przypadku hipoteza alternatywna H 1 mówi o istotnej różnicy pomiędzy tymi wartościami. H 0 : m = m 0 H 1 : m ≠ m 0 Wartość statystyki testującej obliczamy na podstawie wzoru: gdzie: - średnia arytmetyczna - wartość oczekiwana

Jeśli znane jest odchylenie standardowe: gdzie: - średnia arytmetyczna - wartość oczekiwana

Procedura podejmowania decyzji dotyczących przyjęcia lub odrzucenia H 0 przebiega następująco: a) w przypadku testu dwustronnego (H 1: m ≠ m 0) • jeśli wartość obliczona t spełnia nierówność - należy odrzucić H 0 na korzyść H 1, • jeśli natomiast: - nie ma podstaw do odrzucenia H 0. b) w przypadku testu jednostronnego (H 1: m < m 0 lub H 1: m > m 0) • jeśli wartość obliczona t spełnia nierówność - należy odrzucić H 0 na korzyść H 1, • jeśli natomiast: - nie ma podstaw do odrzucenia H 0.

W przypadku, gdy odchylenie standardowe nie jest znane, należy posłużyć się odchyleniem standardowym z próby. Wartość sprawdzianu hipotezy obliczamy wykorzystując następujący wzór: Granicę obszaru krytycznego dla zadanego poziomu istotności α odczytujemy z tablicy rozkładu t-Studenta dla r =n-1 stopni swobody. W przypadku testu dwustronnego (H 1: m ≠ m 0) obszar krytyczny ma postać:

W przypadku testów jednostronnych (H 1: m < m 0 lub H 1: m > m 0) mamy natomiast: lub Jeżeli obliczona wartość t znajdzie się w obszarze krytycznym, to wtedy H 0 należy odrzucić na korzyść hipotezy alternatywnej H 1. W przeciwnym razie nie ma podstaw do jej odrzucenia. Hipoteza zerowa może również przyjąć postać H 0: m ≤ m 0 lub H 0: m ≥ m 0. W pierwszym przypadku hipoteza H 1: m > m 0 a w drugim: H 1: m < m 0. Taki zapis jednoznacznie określa sposób wyznaczenia obszaru krytycznego.

Zadanie przykładowe W 40 wylosowanych zakładach pewnej gałęzi przemysłowej zbadano koszty materiałowe przy produkcji pewnego wyrobu i otrzymano średnią 550 PLN. Zakładając, że poziom kosztów materiałowych ma rozkład N(m, 160), zweryfikować hipotezę na poziomie istotności alfa = 0, 05, że średnie koszty materiałowe przy produkcji tego wyrobu wynoszą 600 PLN.

Przykład Na podstawie badań rynku nieruchomości przeprowadzonych w pierwszym kwartale zeszłego roku obliczono, że średnia cena lokali mieszkalnych w miejscowości B wynosi 6500 zł/m 2. W drugim kwartale zeszłego roku specjalista w pewnej firmie zajmującej się sprzedażą nieruchomości przeprowadził na 25 elementowej próbie podobne badanie i stwierdził, że średnia cena lokali mieszkalnych wyniosła 6560 zł/m 2 a odchylenie standardowe 250 zł/m 2. Czy oznacza to, że ceny nieruchomości wzrosły? Należy przyjąć poziom istotności α = 0, 05.

WERYFIKACJA ISTOTNOŚCI RÓŻNICY MIĘDZY OCZEKIWANYMI DWÓCH ZMIENNYCH LOSOWYCH WARTOŚCIAMI

W zbadanej losowo próbie 150 rodzin zamieszkałych w Krakowie średnie miesięczne wydatki na mieszkanie wynosiły 250 PLN z odchyleniem standardowym równym 100 PLN. W podobnej 100 -elementowej próbie rodzin zamieszkałych we Wrocławiu średnie miesięczne wydatki na mieszkanie wynosiły 200 PLN z odchyleniem standardowym równym 80 PLN. Czy otrzymane wyniki potwierdzają hipotezę zerową, że średnie wydatki na mieszkanie w Krakowie nie są wyższe niż we Wrocławiu? Przyjąć poziom istotności alfa = 0, 05. H 0 : m 1 ≤ m 2 H 1 : m 1 > m 2

Jeśli wartość obliczona t spełnia nierówność , gdzie r = (n 1 -1)+ (n 2 -1) stopni swobody - należy odrzucić H 0 na korzyść H 1, Jeżeli natomiast: - przeto nie ma podstaw do odrzucenia H 0.

Zadanie przykładowe Wysunięto hipotezę, że muzyka przy warsztatach zwiększa wydajność pracy robotników. Wylosowano grupę 8 robotników i zmierzono ich wydajność pracy przed i po umieszczeniu przy ich stanowiskach głośników, z których nadawano cicho muzykę. Wydajności (liczba sztuk na godzinę) przed i po zastosowaniu głośników były następujące: Przed Po Średnia = 30 Średnia =32 Odch. standardowe = 5 Odch. standardowe =7 Zakładając, że wydajność pracy ma rozkład normalny zweryfikować na poziomie istotności alfa = 0, 05 hipotezę, że wydajność pracy przy muzyce wzrasta.

H 0 : m 1 = m 2 H 1 : m 1 < m 2

* Niech cecha X ma w zbiorowości generalnej rozkład N(m, σ). Należy zweryfikować hipotezę H 0: σ2=σ20 przeciwko H 1: σ2>σ20. Taką hipotezę alternatywną przyjmuje się najczęściej, gdyż zwykle sytuacja, gdy wariancja cechy w zbiorowości jest duża, jest niekorzystna. Jeśli m jest znane, to sprawdzian hipotezy H 0 ma postać: Przy założeniu prawdziwości H 0 statystyka ta ma rozkład χ2 o n stopniach swobody.

Jeśli m jest nieznane, sprawdzianem H 0 hipotezy jest: Statystyka ta ma rozkład χ2 o n-1 stopniach swobody. Z uwagi na postać H 1 relacja P(χ2>χ2α)=α wyznacza prawostronny zbiór krytyczny, gdzie χ2α jest wartością krytyczną odczytaną z tablic rozkładu χ2 dla odpowiedniej liczby stopni swobody i P=α. Jeśli dla danej próby losowej relacja wyznaczająca zbiór krytyczny jest spełniona, to H 0 należy odrzucić na korzyść H 1.

Zadanie przykładowe Średnie odchylenie od normy pracochłonności przy produkcji wyrobu pojedynczego robotnika powinno wynosić 7, 9 min/wyrób. Wylosowano 20 robotników, których odchylenie standardowe pracochłonności wynosiło 8, 4 min/wyrób. Przyjmując poziom istotności 0, 01 zweryfikować hipotezę o równości faktycznego i zakładanego odchylenia standardowego.

Jeśli n>30, sprawdzian hipotezy przyjmuje jedną z poniższych postaci: Jeśli m jest znane w zbiorowości generalnej, to Jeśli m jest nieznane, wówczas Statystyka T ma rozkład zbliżony do N(0, 1), zatem dalsze postępowanie jest identyczne jak w opisanych wcześniej testach istotności wykorzystujących statystyki o rozkładzie N(0, 1).

* Badamy dwie zbiorowości o rozkładzie normalnym N(m 1, σ1) i N(m 2, σ2). Należy zweryfikować hipotezę: H 0: σ21=σ22 przy H 1: σ21>σ22. Z obydwu populacji losuje się próby proste o liczebności n 1 i n 2. Niech S 2(1) i S 2(2) oznaczają wariancję S 2. Ze względu na postać hipotezy H 1 tak numerujemy zbiorowości, aby S 2(1)>S 2(2). Sprawdzianem hipotezy jest statystyka: Statystyka ta ma rozkład F-Snedecora o r 1=(n 1 -1) i r 2=(n 2 -1) stopniach swobody. Relacja wyznaczająca prawostronny zbiór krytyczny jest postaci: P(F>Fα)=α, Gdzie Fα odczytujemy z tablic rozkładu F-Snedecora dla r 1 i r 2 stopni swobody.

Zadanie przykładowe Dla porównania regularności uzyskiwanych wyników sportowych dwóch zawodników (skok w dal) w pewnym okresie czasu wylosowano 7 wyników skoków dwóch zawodników, otrzymując rezultaty: Zawodnik A Średnia =8, 01 m Odch. standardowe =0, 05 m Zawodnik B Średnia =7, 99 m Odch. standardowe =0, 1 m Na poziomie istotności alfa = 0, 05 zweryfikować hipotezę o jednakowej regularności uzyskiwanych wyników (tzn. hipotezę, że wariancje rezultatów obu zawodników są równe) wobec hipotezy alternatywnej, że regularność pierwszego zawodnika jest wyższa. H 0: σ21=σ22 przy H 1: σ21>σ22.