Versin Junio de 2019 FSICA GENERAL II Tema

Versión: Junio de 2019

FÍSICA GENERAL II Tema 1: Termodinámica I Tema 2: Termodinámica II Tema 3: Campo eléctrico I Tema 4: Campo eléctrico II Tema 5: Corriente eléctrica Tema 6: Campo magnético I Tema 5: Corriente eléctrica • Transporte de cargas bajo diferencias de potencial. Intensidad y densidad de corriente • Conductividad y resistividad. Conductancia y resistencia. Ley de Ohm. Asociaciones de resistencias. Ley de Ohm local. Tema 7: Campo magnético II • Fuerza electromotriz y circuitos. Leyes de Kirchhoff en circuitos resistivos. Tema 8: Inducción electromagnética I • Energía y potencia en circuitos eléctricos Tema 9: Corriente alterna Tema 10: Ondas mecánicas Tema 11: Ecuaciones de Maxwell y ondas electromagnéticas Tema 12: Óptica Tema 13: Relatividad restringida Tema 14: Estructura de la materia II

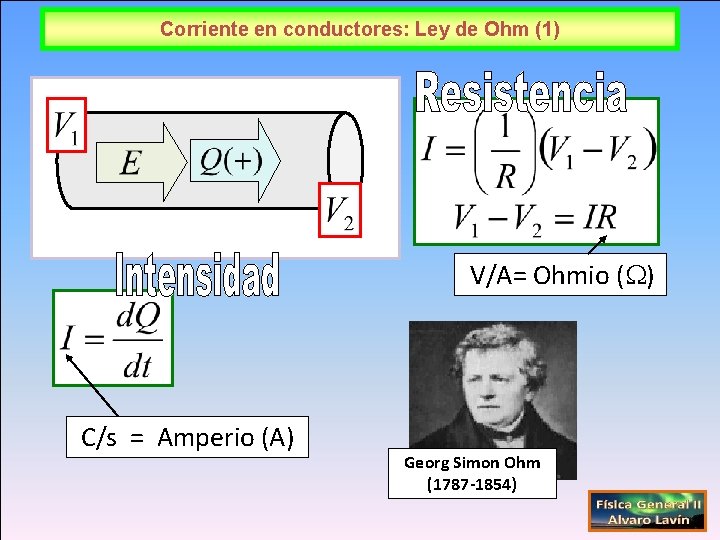
Corriente en conductores: Ley de Ohm (1) V/A= Ohmio ( ) C/s = Amperio (A) Georg Simon Ohm (1787 -1854)

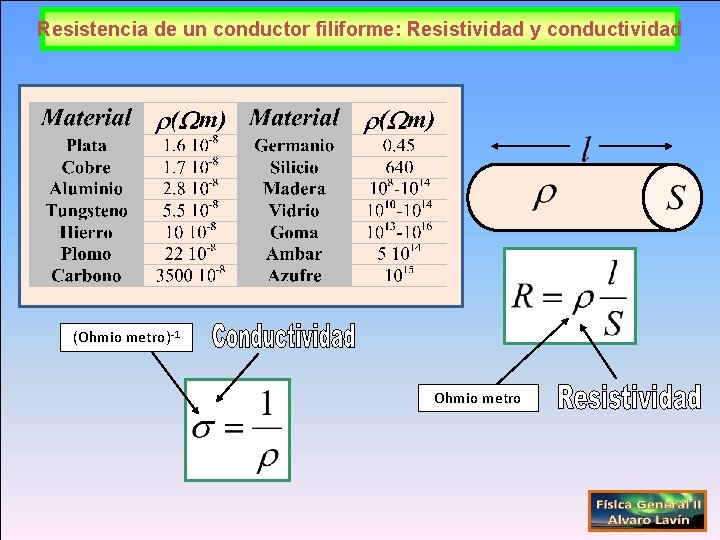
Resistencia de un conductor filiforme: Resistividad y conductividad (Ohmio metro)-1 Ohmio metro

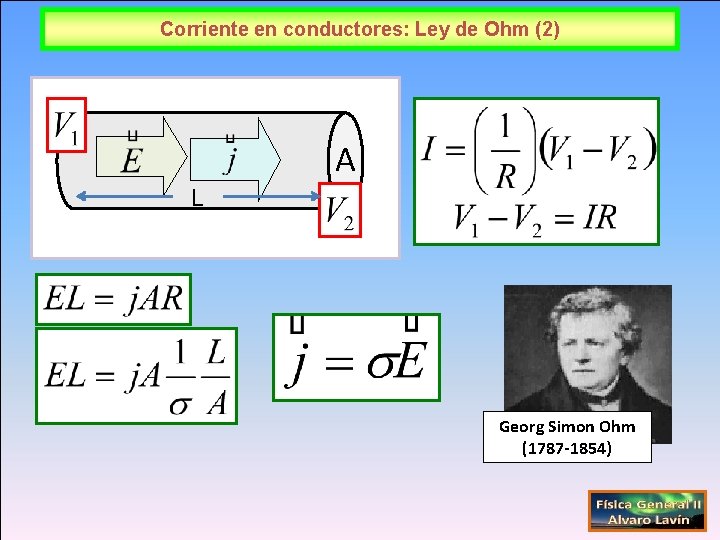
Corriente en conductores: Ley de Ohm (2) A L Georg Simon Ohm (1787 -1854)

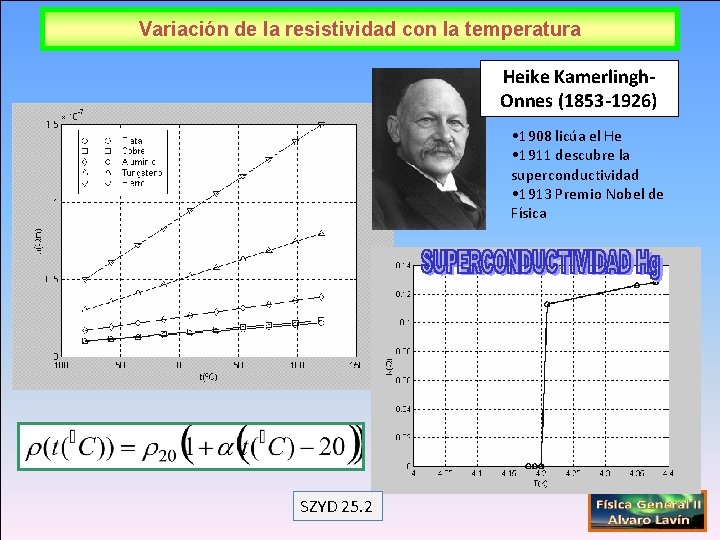
Variación de la resistividad con la temperatura Heike Kamerlingh. Onnes (1853 -1926) • 1908 licúa el He • 1911 descubre la superconductividad • 1913 Premio Nobel de Física SZYD 25. 2

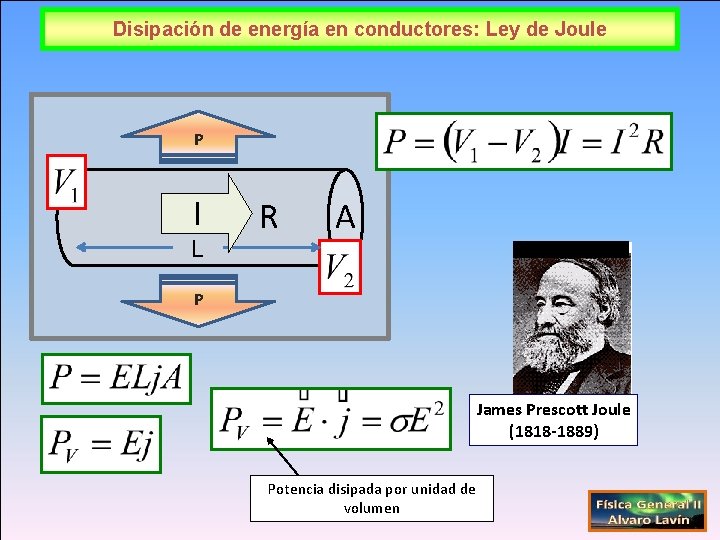
Disipación de energía en conductores: Ley de Joule P I L R A P James Prescott Joule (1818 -1889) Potencia disipada por unidad de volumen

• la resistencia del conductor • la potencia disipada en forma de calor a lo largo del conductor • la densidad de corriente que atraviesa una sección del conductor • la densidad de electrones de conducción • la velocidad media a la que se mueven los electrones de conducción en el conductor

• La conductividad del cobre • La densidad de corriente en el conductor • El campo eléctrico en el interior del conductor • La potencia que disipa la resistencia en forma de calor

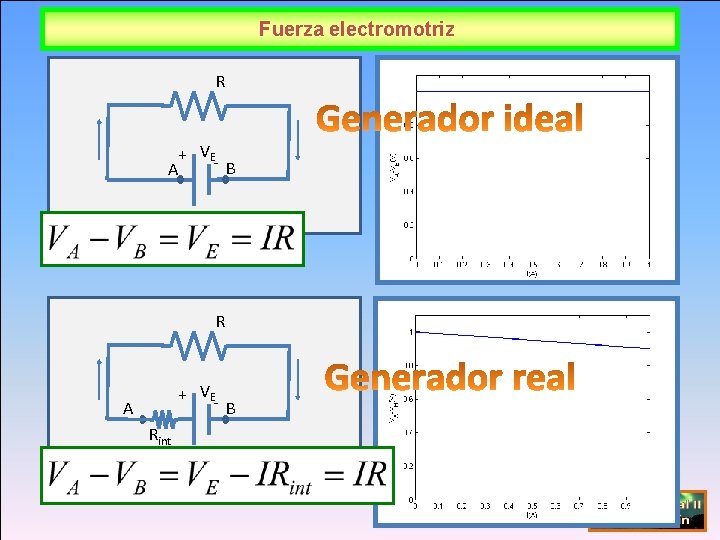
Fuerza electromotriz R + VEB A Rint

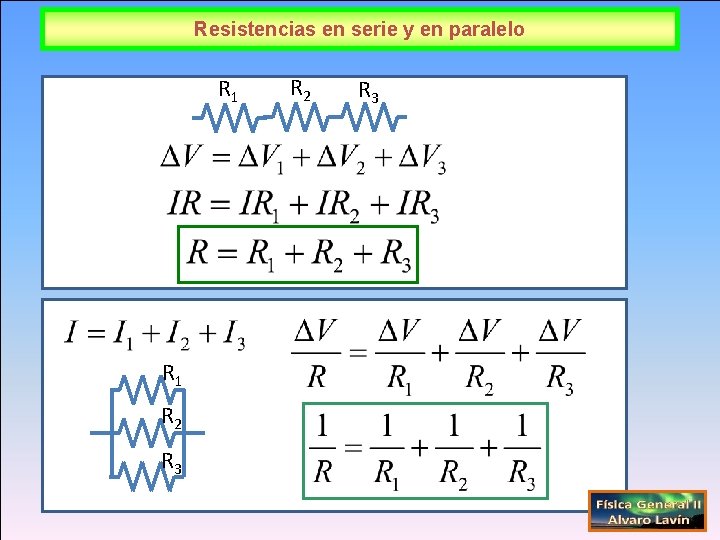
Resistencias en serie y en paralelo R 1 R 2 R 3

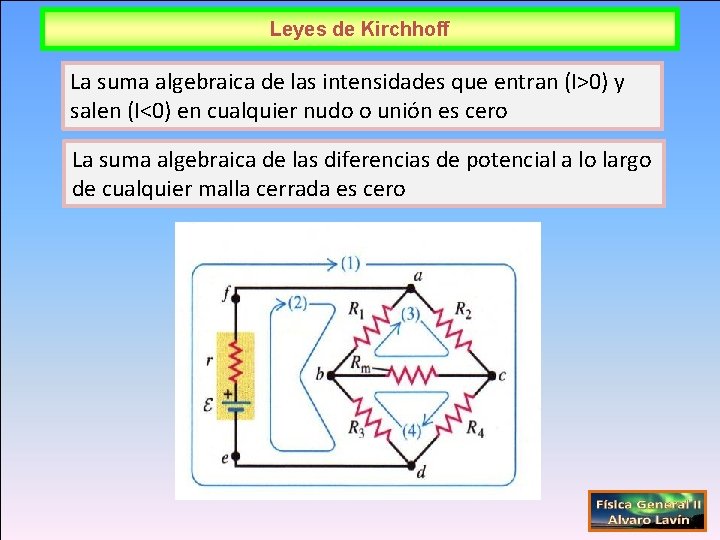
Leyes de Kirchhoff La suma algebraica de las intensidades que entran (I>0) y salen (I<0) en cualquier nudo o unión es cero La suma algebraica de las diferencias de potencial a lo largo de cualquier malla cerrada es cero

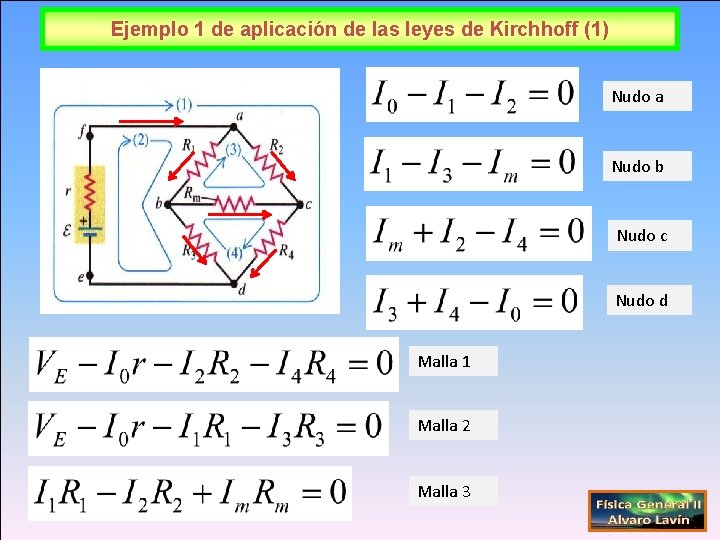
Ejemplo 1 de aplicación de las leyes de Kirchhoff (1) Nudo a Nudo b Nudo c Nudo d Malla 1 Malla 2 Malla 3

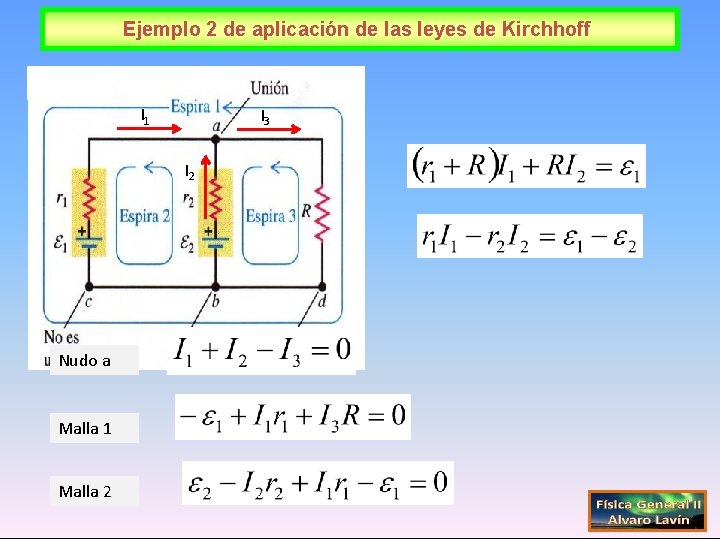
Ejemplo 2 de aplicación de las leyes de Kirchhoff I 1 I 3 I 2 Nudo a Malla 1 Malla 2

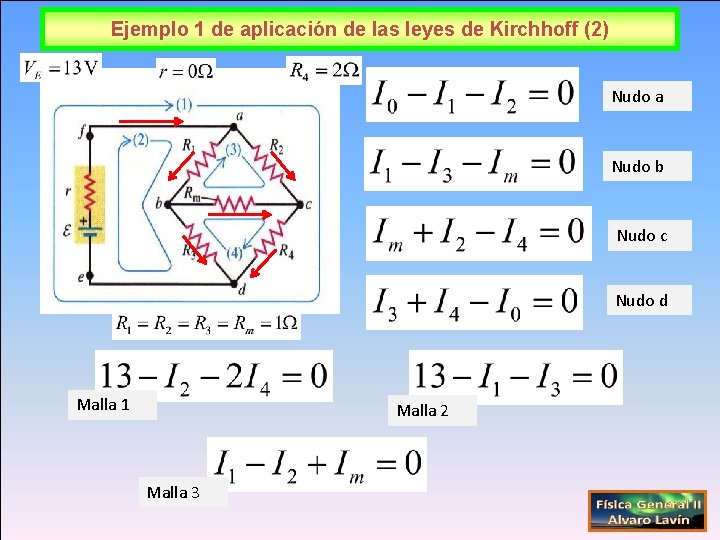
Ejemplo 1 de aplicación de las leyes de Kirchhoff (2) Nudo a Nudo b Nudo c Nudo d Malla 1 Malla 2 Malla 3

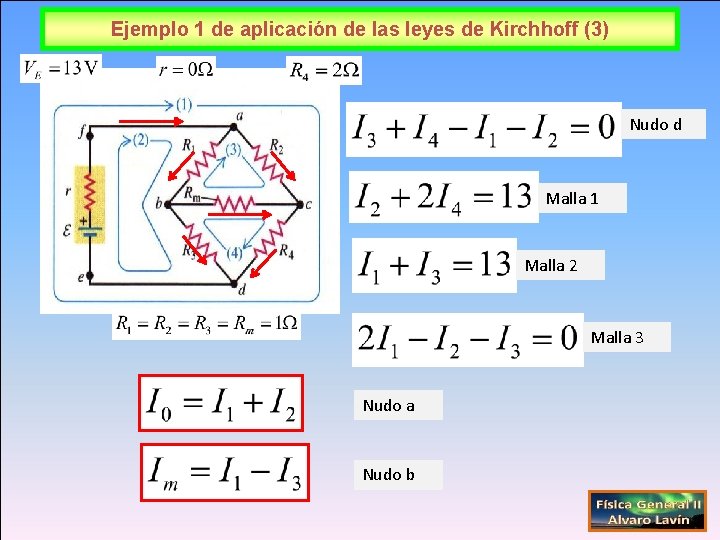
Ejemplo 1 de aplicación de las leyes de Kirchhoff (3) Nudo d Malla 1 Malla 2 Malla 3 Nudo a Nudo b

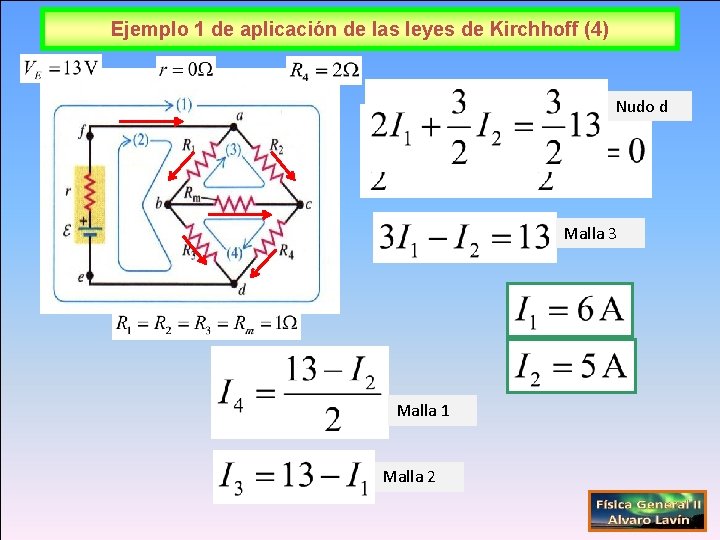
Ejemplo 1 de aplicación de las leyes de Kirchhoff (4) Nudo d Malla 3 Malla 1 Malla 2

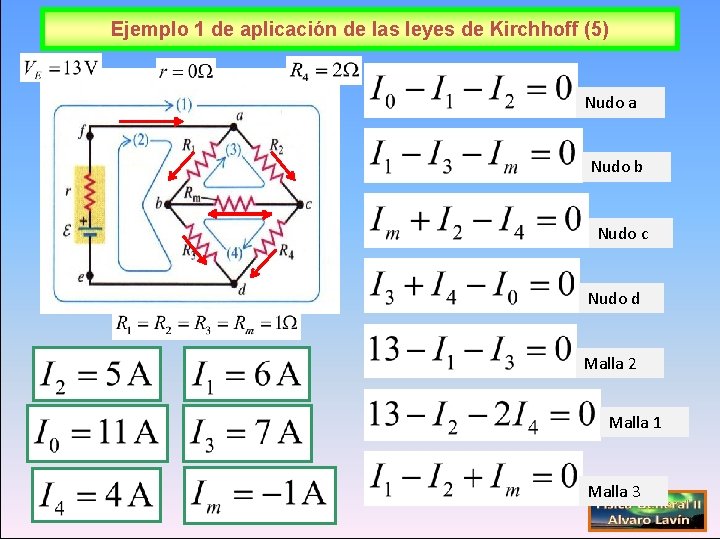
Ejemplo 1 de aplicación de las leyes de Kirchhoff (5) Nudo a Nudo b Nudo c Nudo d Malla 2 Malla 1 Malla 3

En el circuito de la figura I 1=2 A, I 2=3 A, I 4=5 A, R 2=4Ω, R 3=3Ω y R 4=6Ω. Se pide calcular: Las fuerzas electromotrices de las baterías 1 y 2 en V Como nos dan los sentidos y valores de I 2=3 A e I 4=5 A la ley de los nudos nos permite determinar el valor de I 3=8 A y su sentido ‘hacia arriba’ en el dibujo. La ley de las mallas aplicada a las mallas señaladas en el dibujo con el sentido de recorrido indicado nos da las ecuaciones:

En el circuito de la figura I 1=2 A, I 2=3 A, I 4=5 A, R 2=4Ω, R 3=3Ω y R 4=6Ω. Se pide calcular: La potencia que suministran cada una de las baterías al circuito en W Como nos dan el sentido y valor de I 2=3 A e I 1=2 A la ley de los nudos nos permite determinar el valor de la intensidad que circula por la rama del circuito de la batería 1 IVE 1=1 A Como nos dan el sentido y valor de I 4=5 A e I 1=2 A la ley de los nudos nos permite determinar el valor de la intensidad que circula por la rama del circuito de la batería 1 IVE 2=7 A

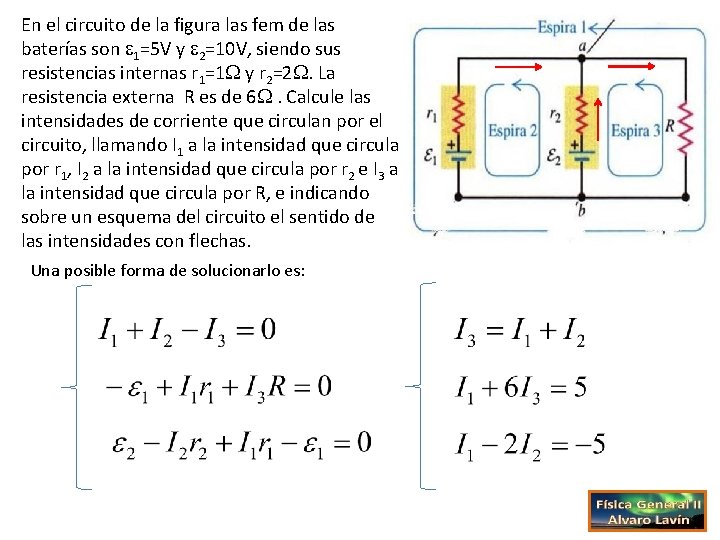
En el circuito de la figura las fem de las baterías son 1=5 V y 2=10 V, siendo sus resistencias internas r 1=1 y r 2=2. La resistencia externa R es de 6 . Calcule las intensidades de corriente que circulan por el circuito, llamando I 1 a la intensidad que circula por r 1, I 2 a la intensidad que circula por r 2 e I 3 a la intensidad que circula por R, e indicando sobre un esquema del circuito el sentido de las intensidades con flechas. Una posible forma de solucionarlo es:

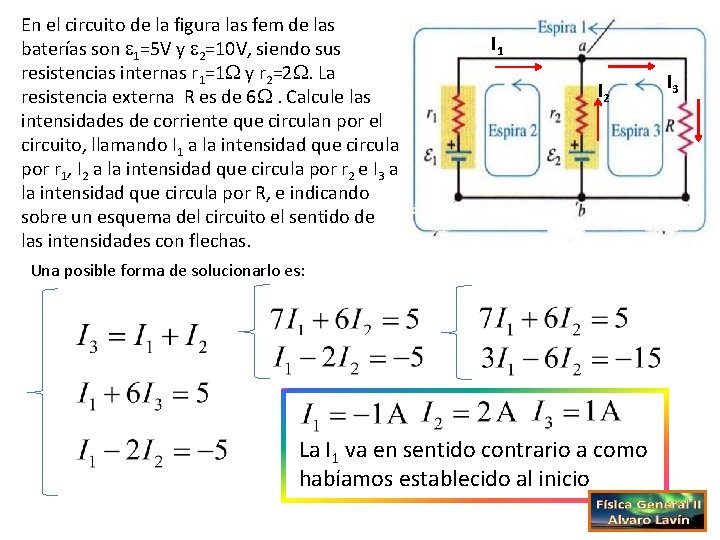
En el circuito de la figura las fem de las baterías son 1=5 V y 2=10 V, siendo sus resistencias internas r 1=1 y r 2=2. La resistencia externa R es de 6 . Calcule las intensidades de corriente que circulan por el circuito, llamando I 1 a la intensidad que circula por r 1, I 2 a la intensidad que circula por r 2 e I 3 a la intensidad que circula por R, e indicando sobre un esquema del circuito el sentido de las intensidades con flechas. I 1 I 2 Una posible forma de solucionarlo es: La I 1 va en sentido contrario a como habíamos establecido al inicio I 3

En el circuito de la figura R 1=R 2=R 3=2Ω, R 4=3Ω, R 5=6Ω y las baterías son iguales suministrando una tensión de 6 V. Calcule las intensidades de corriente I 1 e I 2 señaladas en la figura que circulan por las ramas del circuito. Llamando I 3 a la intensidad que circula por la rama de la resistencia R 3 Como las resistencias 4 y 5 están en paralelo pueden ser sustituidas por su resistencia equivalente La ley de las mallas aplicada a las mallas señaladas en el dibujo con el sentido de recorrido indicado nos da las ecuaciones: Combinándolas con la ecuación del nudo obtenemos: Sistema de ecuaciones cuya solución es:

En el circuito de la figura R 1=2 , R 2=2 , R 3=2 y R 4=4 , VE=16 V y C=3 p. F. Calcule, en el régimen permanente: La intensidad que circula en la rama del condensador En régimen permanente no puede circular intensidad por la rama del condensador. Las intensidades que circulan por las resistencias 1 y 2. Las intensidades que circulan por las resistencias 3 y 4. A B

En el circuito de la figura R 1=2 , R 2=2 , R 3=2 y R 4=4 , VE=16 V y C=3 p. F. Calcule, en el régimen permanente: La carga que ha adquirido el condensador Aplicando la regla de las mallas a la malla del condensador y la pila Suponiendo que el condensador de la primera parte de este ejercicio tiene aire entre sus placas planas r=1. Calcule: La nueva carga del condensador si se introduce entre sus placas una lámina de un material de permitividad relativa r=2 una vez alcanzado de nuevo el régimen permanente. La tensión entre las placas del condensador se mantiene, mientras que la capacidad del condensador se multiplica por 2.

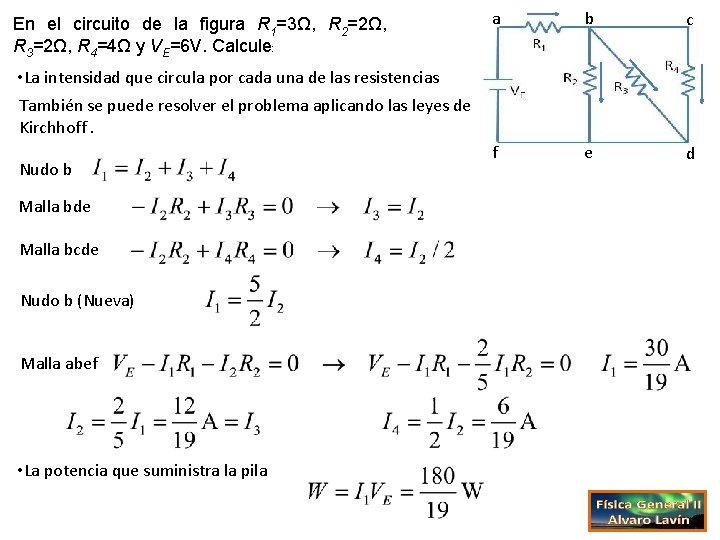
En el circuito de la figura R 1=3Ω, R 2=2Ω, R 3=2Ω, R 4=4Ω y VE=6 V. Calcule: • La intensidad que circula por cada una de las resistencias Se puede resolver el problema de forma muy sencilla si nos damos cuenta de que el circuito equivale a tres resistencias en paralelo 2, 3 y 4 en serie con 1. A R 1 VE R 2 R 3 R 4 B

En el circuito de la figura R 1=3Ω, R 2=2Ω, R 3=2Ω, R 4=4Ω y VE=6 V. Calcule: a b c f e d • La intensidad que circula por cada una de las resistencias También se puede resolver el problema aplicando las leyes de Kirchhoff. Nudo b Malla bde Malla bcde Nudo b (Nueva) Malla abef • La potencia que suministra la pila

• Las intensidades que circulan por las resistencias En las condiciones indicadas no circula intensidad por las ramas de los condensadores. Un posible conjunto de condiciones que resuelven el problema es: Con los datos numéricos del enunciado la solución es: En este caso también pueden utilizarse las expresiones de las resistencias equivalentes de combinaciones de resistencias en serie y en paralelo para resolver el problema ya que, ignorando los condensadores, R 2 y R 4 están en serie entre sí y en paralelo con R 3 y esta combinación R 3, R 2 y R 4 está en serie con R 1.

• Las cargas de los condensadores Aplicando leyes de las mallas que incluyan las ramas de los condensadores Sustituyendo los valores numéricos y las intensidades que recorren el circuito obtenidas en el apartado anterior:

En el circuito de la figura R=2 , VE=16 V y C=3 p. F. En el instante inicial el circuito queda cerrado y comienza a cargarse el condensador. Obtenga: • La intensidad como función del tiempo a lo largo de todo el proceso de carga Aplicando la regla de las mallas al circuito …derivando con respecto al tiempo… …ecuación diferencial cuya solución es…

En el circuito de la figura R=2 , VE=16 V y C=3 p. F. En el instante inicial el circuito queda cerrado y comienza a cargarse el condensador. Obtenga: • La tensión final entre las placas del condensador y la carga final que adquiere. Cuando se ha cargado el condensador ya no circula intensidad. La regla de las mallas aplicada al circuito es… • La energía queda almacenada en forma de campo electrostático en el condensador.

En el circuito de la figura R=2 , VE=16 V y C=3 p. F. En el instante inicial el circuito queda cerrado y comienza a cargarse el condensador. Obtenga: • El trabajo total que realiza la batería a lo largo del proceso. La potencia que desarrolla la batería en un instante es… El trabajo que realiza a lo largo de todo el proceso… • La energía disipada por efecto Joule en la resistencia. La potencia que disipa la resistencia en un instante es… El calor disipado a lo largo de todo el proceso…

Publicaciones del Departamento de Física Aplicada: • PROBLEMAS DE FÍSICA, J. J. Scala, Sociedad de Amigos de la ETSII. (Capítulo 10: Electrocinética C. C. ) Obras generales: • FISICA UNIVERSITARIA I y II, Sears, Zemansky, Young, Freedman, Ed. Addison. Wesley Capítulos 25 -26 (Tomo 2) • FÍSICA PARA LA CIENCIA Y LA TECNOLOGÍA I y II, Tipler, Ed. Reverte Capítulo 26 (Tomo 2)