Dinmica del Punto Versin 07072016 FSICA GENERAL I

























































- Slides: 107

Dinámica del Punto Versión 07/07/2016

FÍSICA GENERAL I Tema 1: Magnitudes físicas. Unidades y medidas Tema 2: Vectores y sistemas de vectores Tema 3: Estática de sistemas Tema 7: Dinámica del punto Objetivo de la dinámica Leyes de Newton Tema 4: Cinemática del punto Ecuaciones intrínsecas de la dinámica Tema 5: Cinemática del sólido rígido Magnitudes cinéticas Tema 6: Cinemática relativa del punto Trabajo y potencia Tema 7: Dinámica del punto Tema 8: Trabajo y energía I Teoremas fundamentales de la dinámica Tema 9: Trabajo y energía II Sistemas de masa variable Tema 10: Movimiento del punto bajo fuerzas centrales Dinámica del punto material ligado a curvas Tema 11: Dinámica del los sistemas I Dinámica relativa del punto: fuerzas de inercia Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II

ISAAC NEWTON Y LA MECÁNICA PHILOSOPHIAE NATURALIS PRINCIPIA MATHEMATICA (1687) • Libro I: Leyes de Newton. • Libro II: Estudio de los fluidos y el movimiento de los cuerpos a través de los fluidos. ISAAC NEWTON (1642 -1727) • Libro III: Ley de Gravitación Universal. Explicación del movimiento de los planetas y sus satélites a partir de la ley de gravitación y las leyes del movimiento del primer libro. NATURE AND NATURE’S LAWS LAY HID IN NIGHT GOD SAID, LET NEWTON BE! AND ALL WAS LIGHT ALEXANDER POPE (1688 -1744)

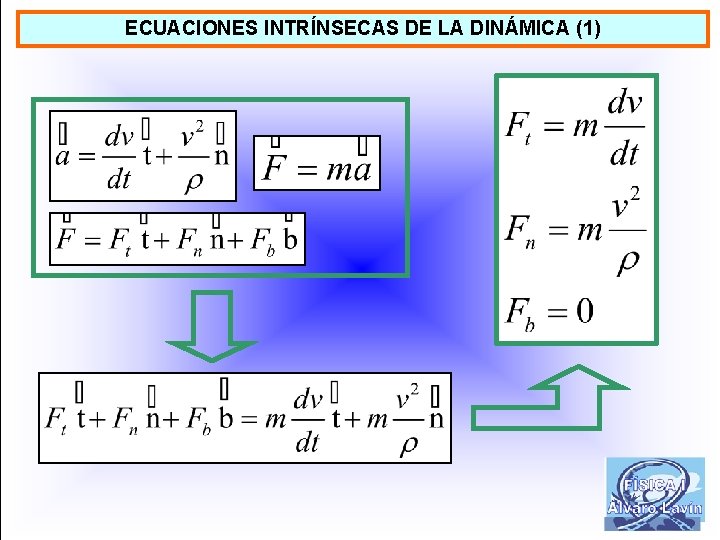
ECUACIONES INTRÍNSECAS DE LA DINÁMICA (1)

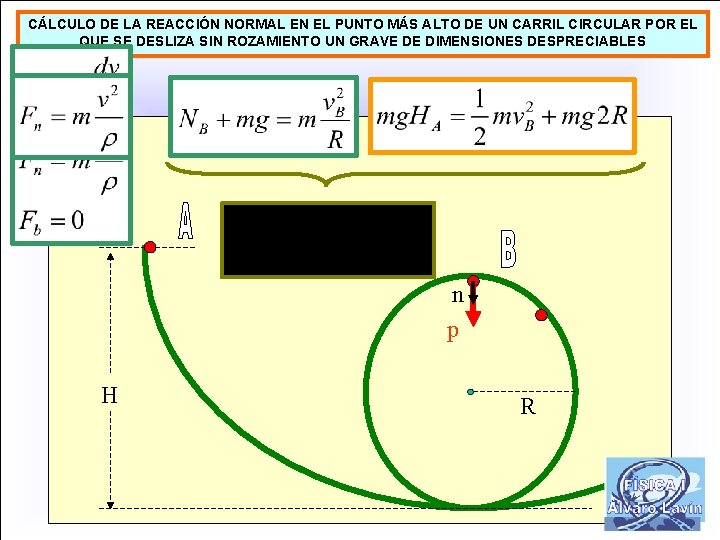
CÁLCULO DE LA REACCIÓN NORMAL EN EL PUNTO MÁS ALTO DE UN CARRIL CIRCULAR POR EL QUE SE DESLIZA SIN ROZAMIENTO UN GRAVE DE DIMENSIONES DESPRECIABLES n p H R

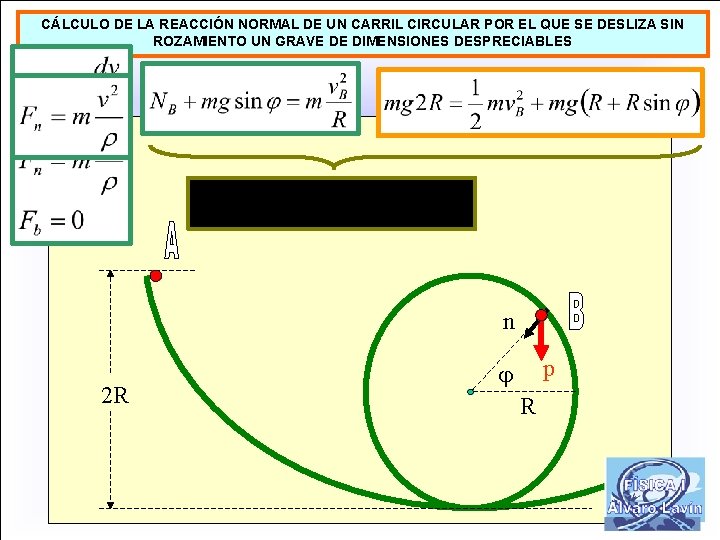
CÁLCULO DE LA REACCIÓN NORMAL DE UN CARRIL CIRCULAR POR EL QUE SE DESLIZA SIN ROZAMIENTO UN GRAVE DE DIMENSIONES DESPRECIABLES n 2 R p R

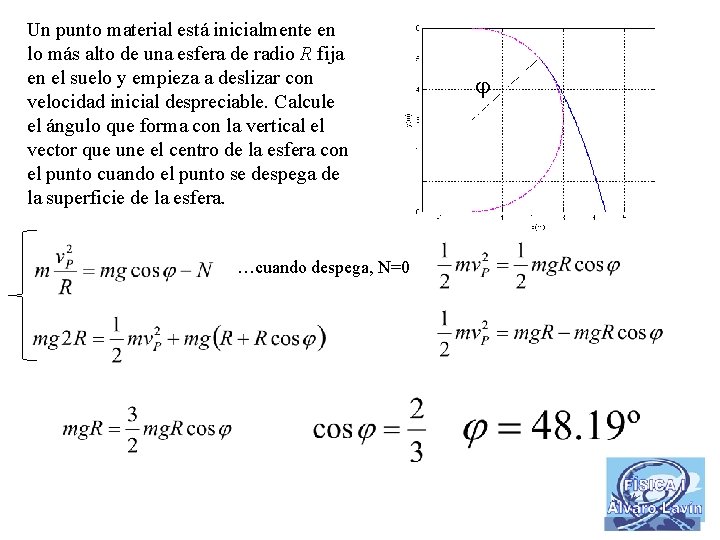
Un punto material está inicialmente en lo más alto de una esfera de radio R fija en el suelo y empieza a deslizar con velocidad inicial despreciable. Calcule el ángulo que forma con la vertical el vector que une el centro de la esfera con el punto cuando el punto se despega de la superficie de la esfera. …cuando despega, N=0

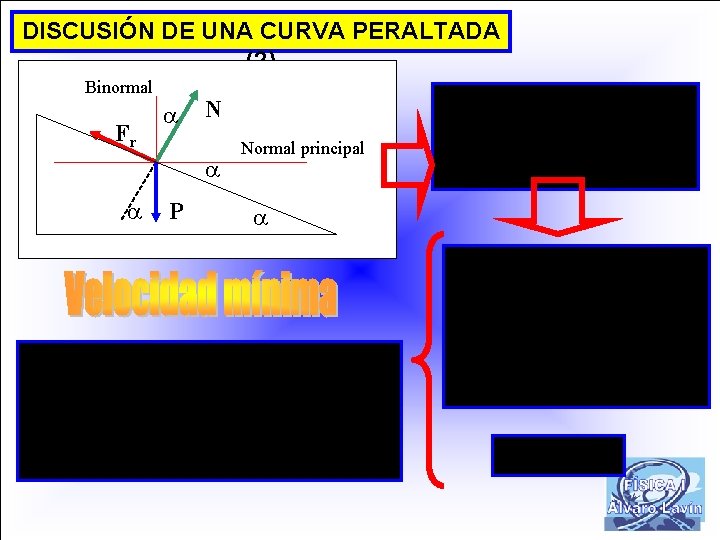
DISCUSIÓN DE UNA CURVA PERALTADA (1) Binormal N P Normal principal Fr

DISCUSIÓN DE UNA CURVA PERALTADA (2) Binormal Fr N P Normal principal

DISCUSIÓN DE UNA CURVA PERALTADA (3) R=200 m =1

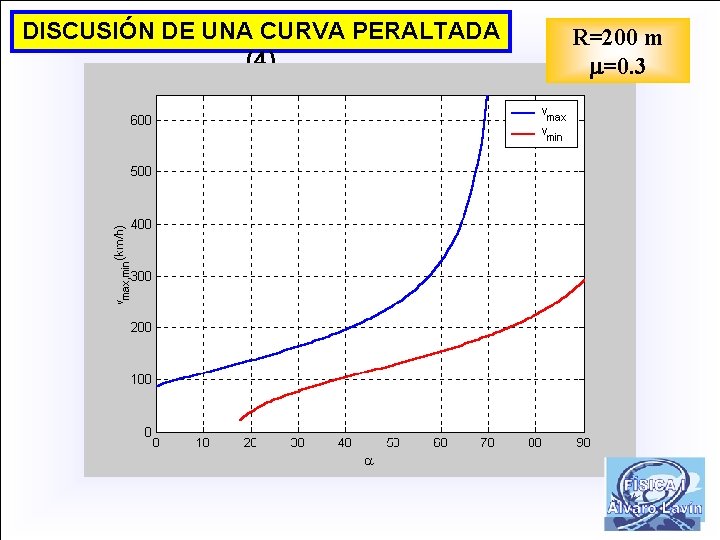
DISCUSIÓN DE UNA CURVA PERALTADA (4) R=200 m =0. 3

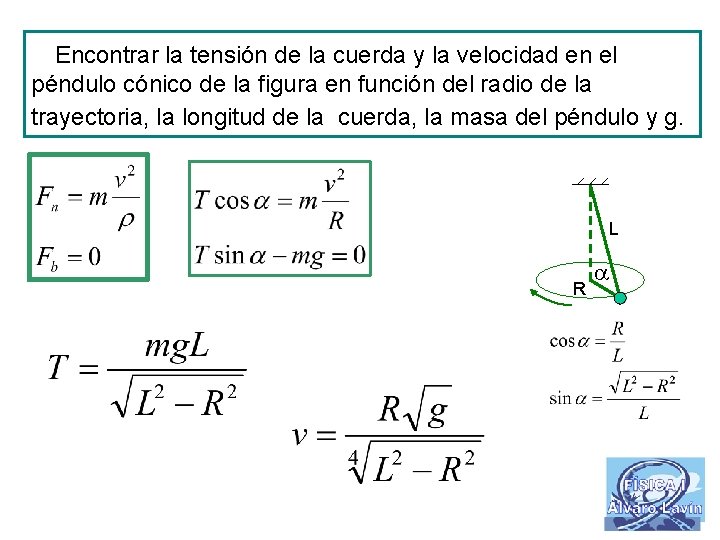
Encontrar la tensión de la cuerda y la velocidad en el péndulo cónico de la figura en función del radio de la trayectoria, la longitud de la cuerda, la masa del péndulo y g. L R

• la aceleración tangencial • la aceleración normal • el radio de curvatura de la trayectoria

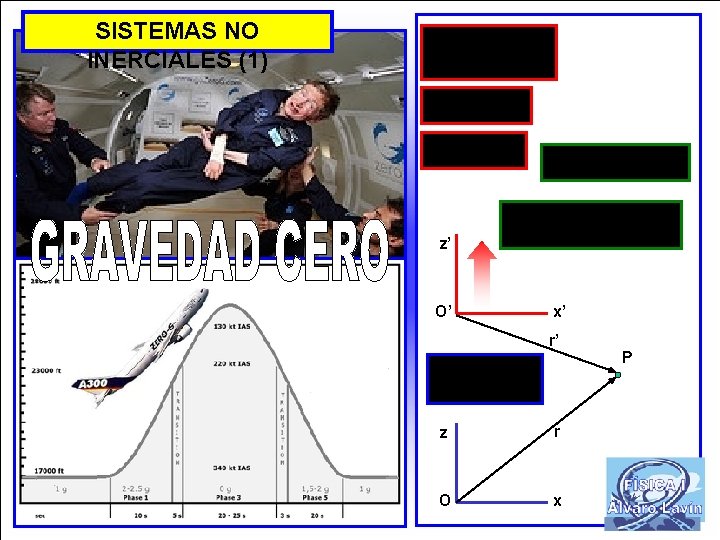
SISTEMAS NO INERCIALES (1) z’ O’ x’ r’ z r O x P

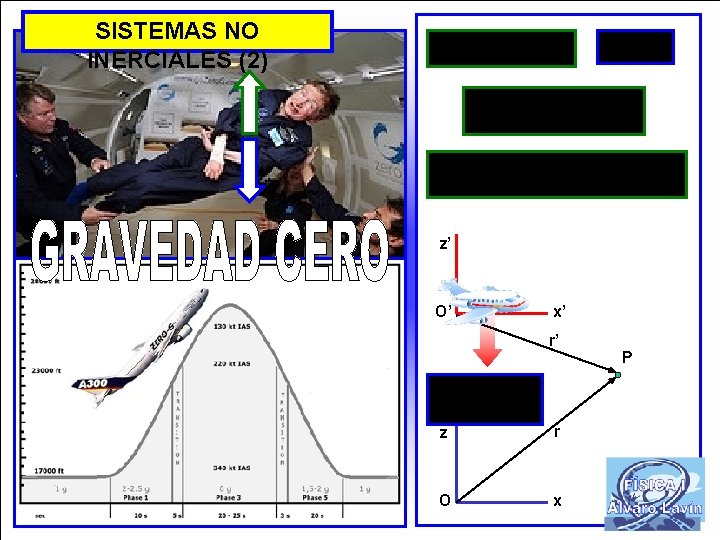
SISTEMAS NO INERCIALES (2) z’ O’ x’ r’ z r O x P

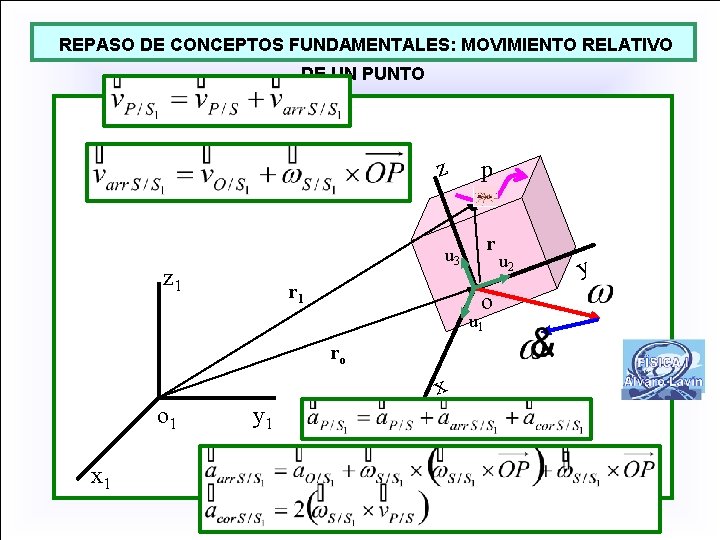
REPASO DE CONCEPTOS FUNDAMENTALES: MOVIMIENTO RELATIVO DE UN PUNTO z p r u 3 z 1 r 1 o u 1 ro x o 1 x 1 y 1 u 2 y

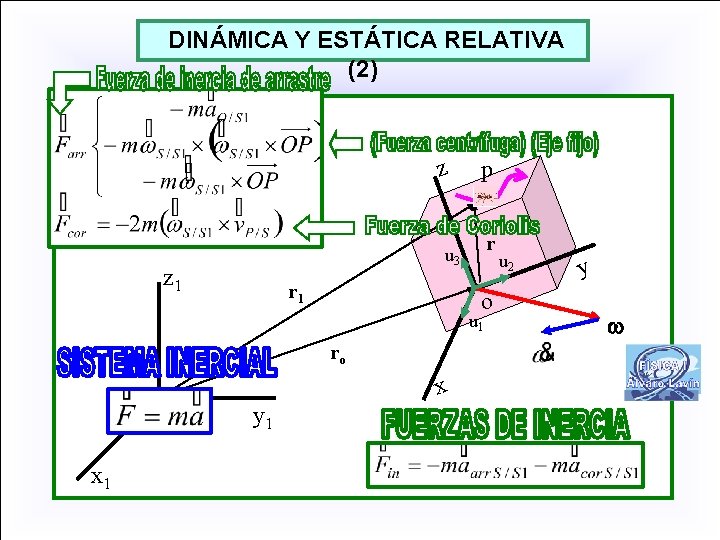
DINÁMICA Y ESTÁTICA RELATIVA (1) z p r u 3 z 1 r 1 o u 1 ro x o 1 x 1 y 1 u 2 y

DINÁMICA Y ESTÁTICA RELATIVA (2) z p r u 3 z 1 r 1 o u 1 ro x o 1 x 1 y 1 u 2 y

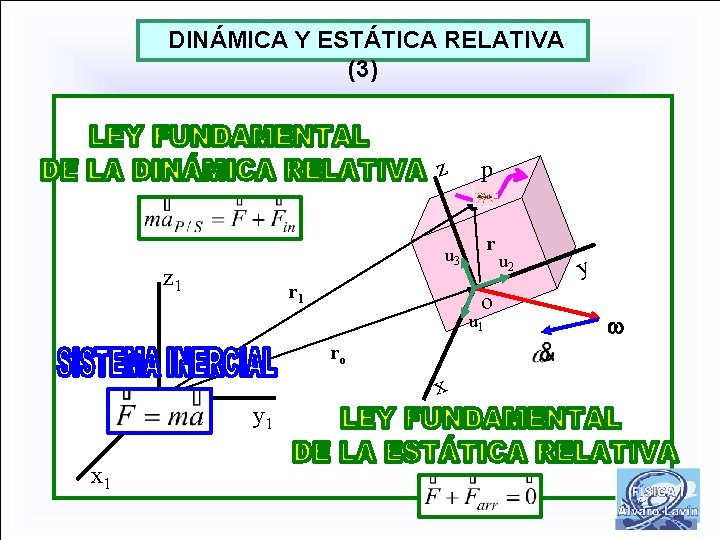
DINÁMICA Y ESTÁTICA RELATIVA (3) z p r u 3 z 1 r 1 o u 1 ro x o 1 x 1 y 1 u 2 y

EQUILIBRIO DE UN OBJETO SOBRE UNA PLATAFORMA GIRATORIA Ec. Intrínsecas de la Dinámica (Sistema Inercial) z 1 El objeto describe una trayectoria Ec. de la Estática con Fuerzas de Inercia (Sistema No Inercial) y y 1 El objeto reposa sobre el eje x x 1 x Examen Jun-

El valor modular máximo de la fuerza de inercia que afecta al bloque y los lugares en que se alcanza La relación que debe haber entre los parámetros físicos que intervienen en el problema para que el bloque no deslice O O 1 Sistema inercial Sistema no inercial

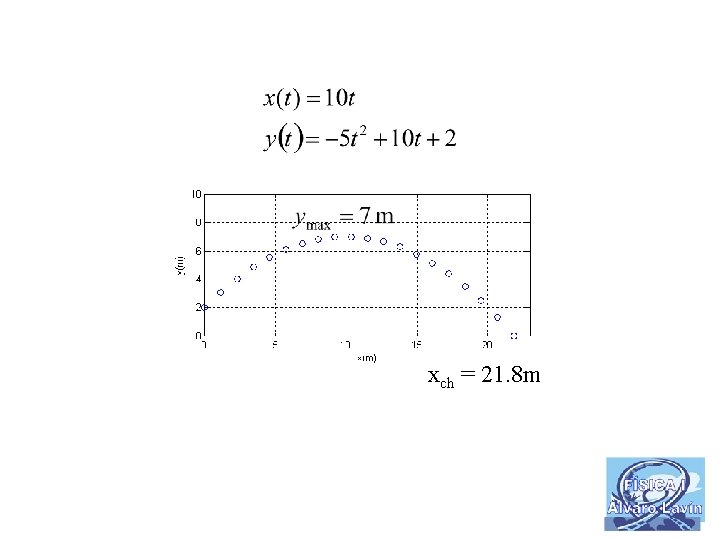
Un lanzador intenta batir el record mundial de lanzamiento de peso (23, 12 m) lanzando una bola con las siguientes condiciones iniciales: x 0=0, y 0=2 m, vx 0=10 m/s y vy 0=10 m/s. Calcule utilizando como gravedad g=10 m/s 2: • Las ecuaciones paramétricas del movimiento de la bola • El tiempo que la bola tarda en chocar con el suelo y la coordenada x del choque De las dos soluciones Condición de choque de la ecuación elegimos t = 2. 18 s ch con el suelo la positiva xch = 21. 8 m

Un lanzador intenta batir el record mundial de lanzamiento de peso (23, 12 m) lanzando una bola con las siguientes condiciones iniciales: x 0=0, y 0=2 m, vx 0=10 m/s y vy 0=10 m/s. Calcule utilizando como gravedad g=10 m/s 2: • El tiempo que la bola tarda en chocar con el suelo y la coordenada x De las dos soluciones del choque de la ecuación elegimos tch = 2. 18 s Condición de choque con el suelo xch = 21. 8 m • La máxima altura que alcanza la bola en el vuelo Cuando se alcanza la máxima altura la componente vertical de la velocidad es nula, por tanto t=1 s la positiva

xch = 21. 8 m

El deportista de alto riesgo Felix Baumgartner se lanzó desde una altura de 39000 m alcanzando en 40 segundos la velocidad de 1173 km/h. Calcule, utilizando un modelo en el que sólo actúa la gravedad: • El tiempo en segundos que tarda en alcanzar esa velocidad • La altura sobre la superficie de la Tierra a la que se encuentra en ese instante

• La velocidad máxima que se da en este movimiento armónico • El tiempo que tarda el objeto en alcanzar por primera vez la velocidad nula



• La resultante de las fuerzas de inercia que actúan sobre la mariquita cuando se encuentra a un metro del centro del disco • La resultante de las fuerzas de reacción horizontales del disco sobre las patas de la mariquita La mariquita se mueve con velocidad rectilínea y constante con respecto al disco; por tanto no tiene aceleración con respecto a este sistema.

PROCEDIMIENTO PARA SOLUCIONAR ECUACIONES DIFERENCIALES DE SEGUNDO ORDEN, LINEALES Y CON COEFICIENTES CONSTANTES HABITUALES EN FÍSICA (1) Soluciones de la ecuación homogénea Solución particular de la ecuación completa

PROCEDIMIENTO PARA SOLUCIONAR ECUACIONES DIFERENCIALES DE SEGUNDO ORDEN, LINEALES Y CON COEFICIENTES CONSTANTES HABITUALES EN FÍSICA (2)

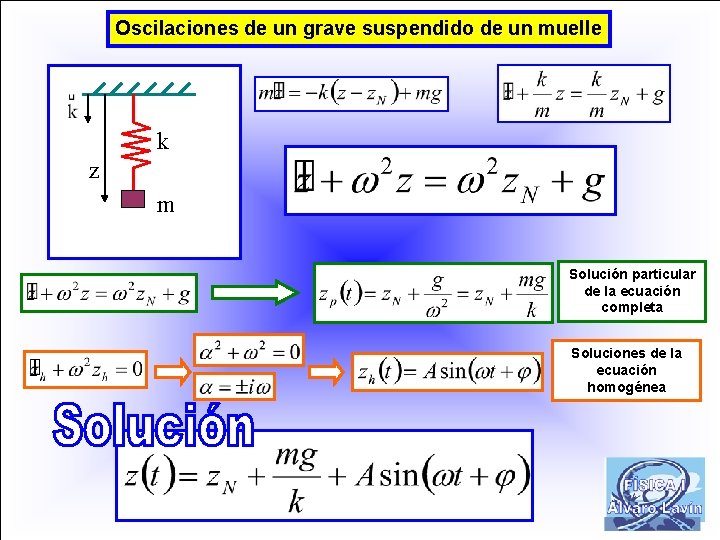
Oscilaciones de un grave suspendido de un muelle k z m Solución particular de la ecuación completa Soluciones de la ecuación homogénea

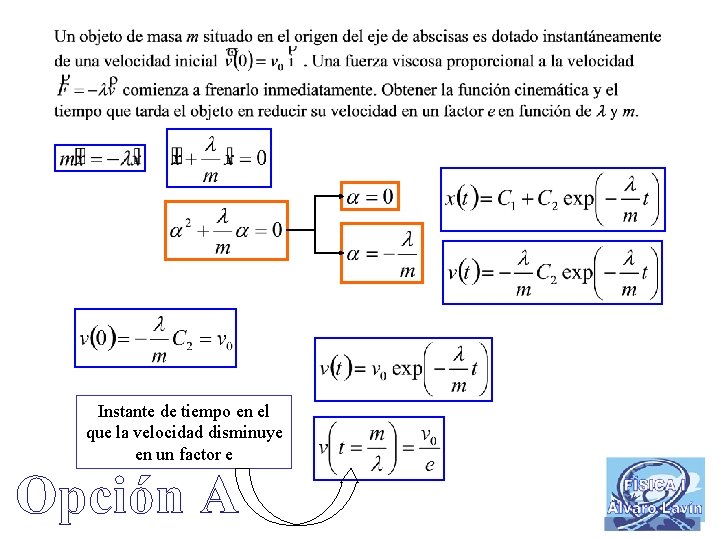
Instante de tiempo en el que la velocidad disminuye en un factor e Opción A

Instante de tiempo en el que la velocidad disminuye en un factor e Opción B

Instante de tiempo en el que la velocidad disminuye en un factor e Opción C

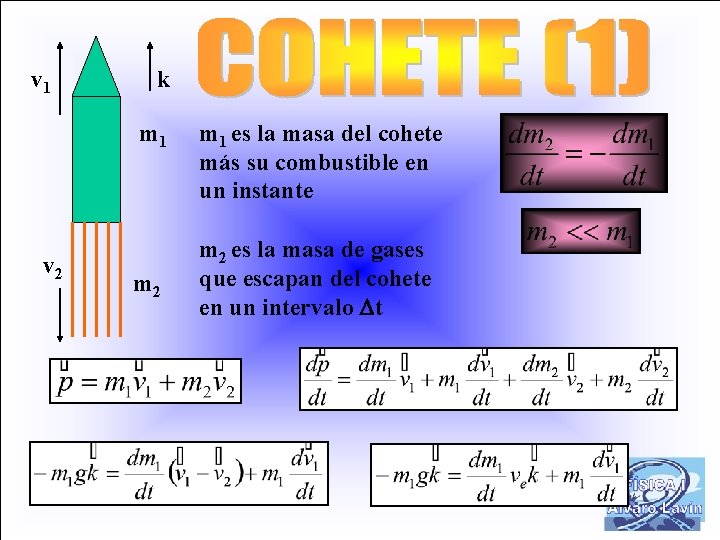
v 1 k m 1 v 2 m 1 es la masa del cohete más su combustible en un instante m 2 es la masa de gases que escapan del cohete en un intervalo t

v 1 k m 1 v 2 m 1 es la masa del cohete más su combustible en un instante m 2 es la masa de gases que escapan del cohete en un intervalo t

v 1 k m 1 v 2 m 2

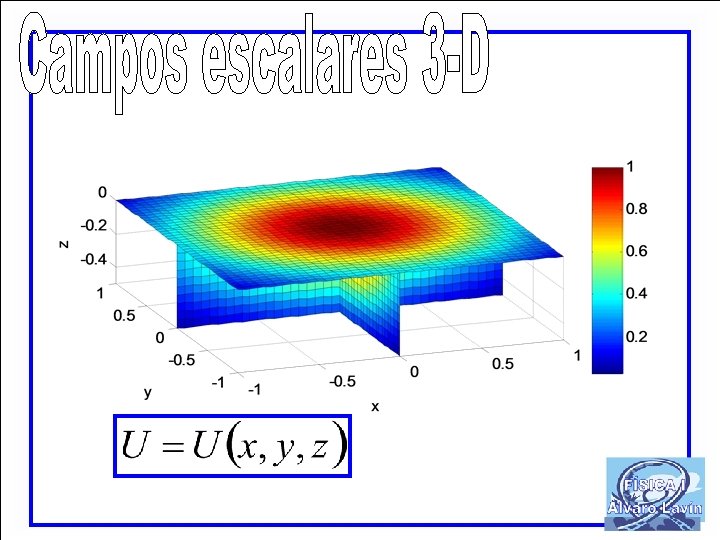
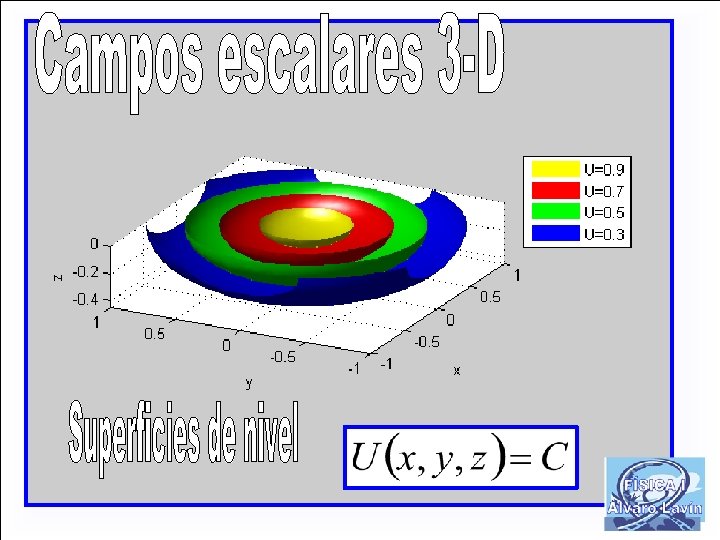
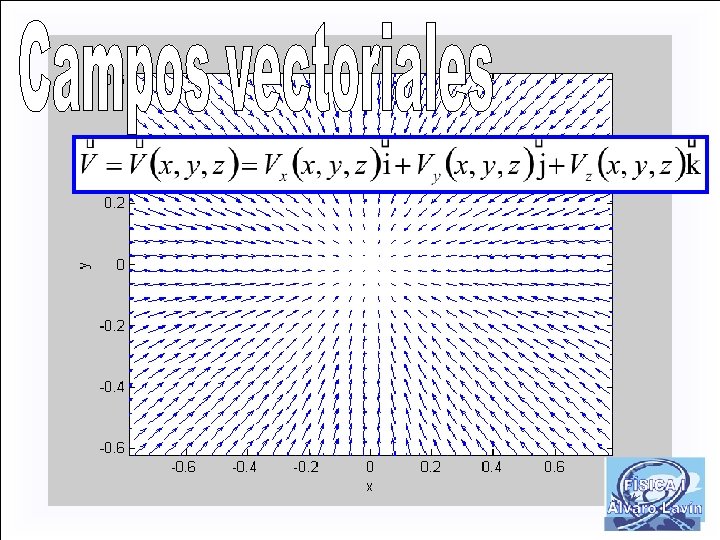
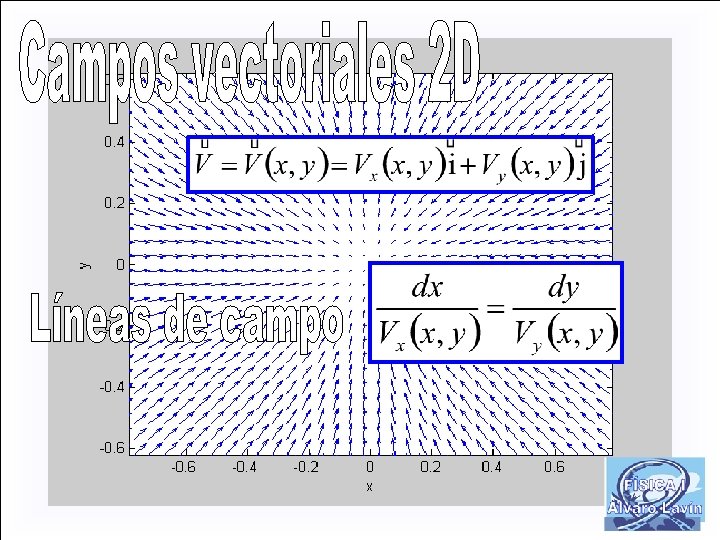
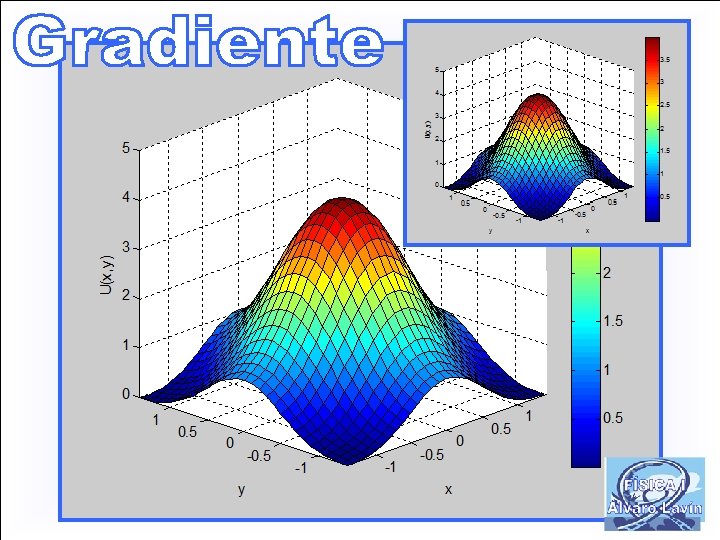
FÍSICA GENERAL I Tema 1: Magnitudes físicas. Unidades y medidas Tema 2: Vectores y sistemas de vectores Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 8: Trabajo y energía I Tema 5: Cinemática del sólido rígido Campos escalares y vectoriales Tema 6: Cinemática relativa del punto Circulación de un campo vectorial Tema 7: Dinámica del punto Gradiente de un campo escalar Tema 8: Trabajo y energía I Función potencial. Campos conservativos Tema 9: Trabajo y energía II Tema 10: Movimiento del punto bajo fuerzas centrales Tema 11: Dinámica del los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II












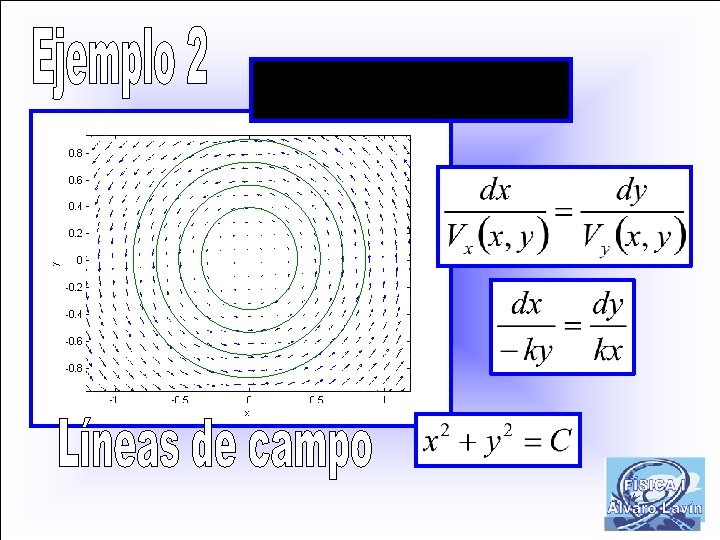
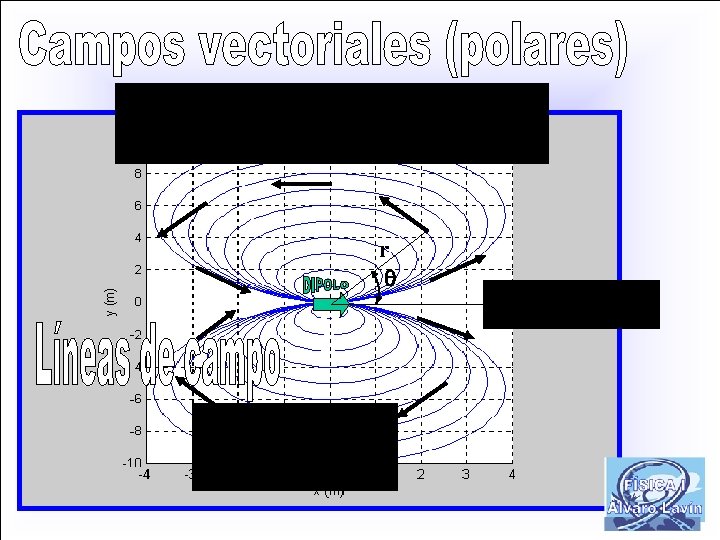
r

r


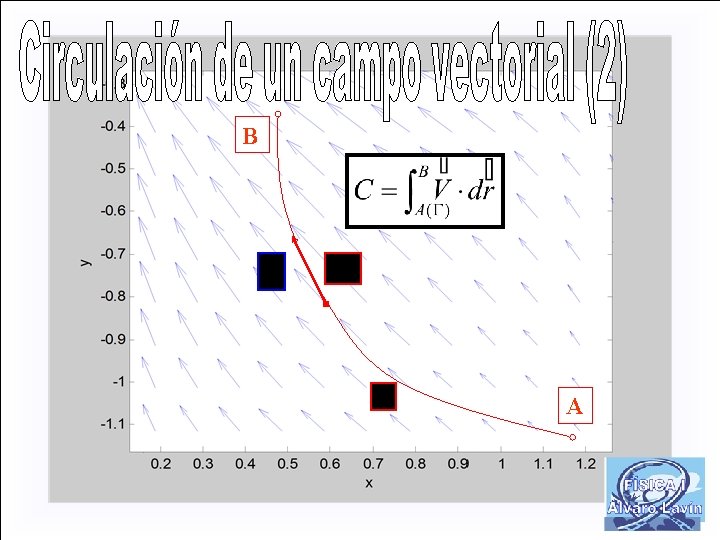
B A

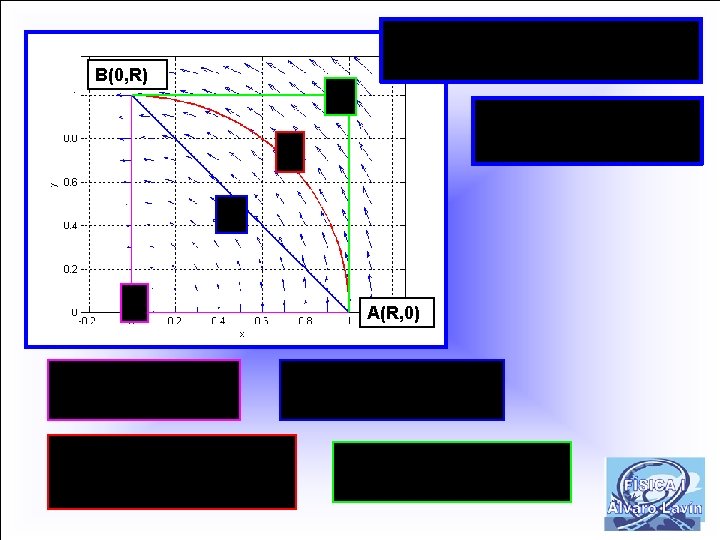
B(0, R) A(R, 0)

Opción B (Polares) Opción A

B(0, R) A(R, 0)

Calcular la circulación del campo vectorial entre los puntos A(0, 0) y B(1, 1) a lo largo de la parábola y=x 2.


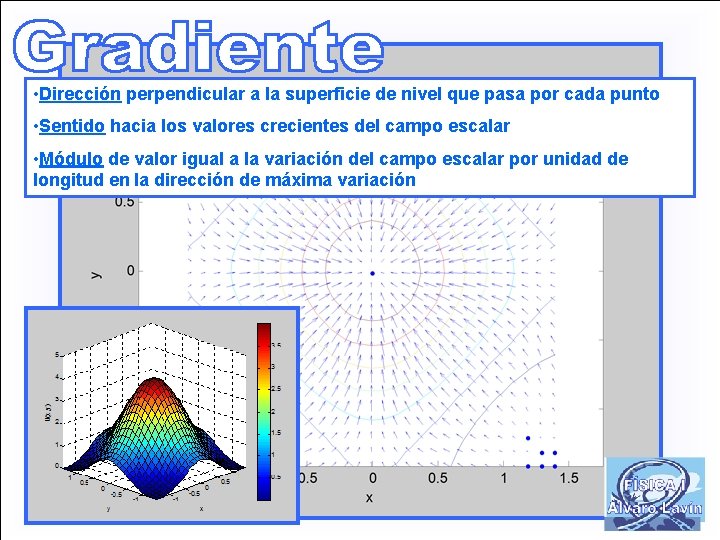
• Dirección perpendicular a la superficie de nivel que pasa por cada punto • Sentido hacia los valores crecientes del campo escalar • Módulo de valor igual a la variación del campo escalar por unidad de longitud en la dirección de máxima variación


• …que la circulación del campo vectorial entre dos puntos cualquiera del espacio sea independiente del camino • …que la circulación en cualquier camino cerrado sea nula • …que el operador rotacional aplicado al campo vectorial dé como resultado un campo vectorial nulo

B(0, R) A(R, 0)

B(0, R) Este campo no puede derivarse de un potencial A(R, 0)

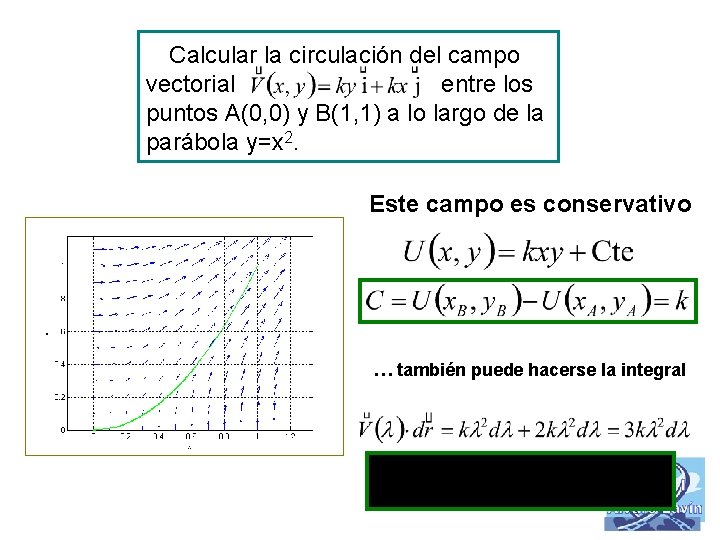
Calcular la circulación del campo vectorial entre los puntos A(0, 0) y B(1, 1) a lo largo de la parábola y=x 2. Este campo es conservativo … también puede hacerse la integral

Calcular la circulación del campo vectorial entre los puntos A(1, 1) y B(2, 8) a lo largo de la curva y=x 3. Este campo es conservativo … también puede hacerse la circulación


FÍSICA GENERAL I Tema 1: Magnitudes físicas. Unidades y medidas Tema 2: Vectores y sistemas de vectores Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 5: Cinemática del sólido rígido Tema 6: Cinemática relativa del punto Tema 7: Dinámica del punto Tema 8: Trabajo y energía I Tema 9: Trabajo y energía II Tema 10: Movimiento del punto bajo fuerzas centrales Tema 11: Dinámica del los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II Tema 9: Trabajo y energía II Movimiento de un punto material bajo fuerzas conservativas Energía potencial Conservación de la energía mecánica Dinámica del movimiento armónico simple: energías cinética y potencial Oscilador amortiguado Movimiento de un grave en un fluido viscoso

• …que la circulación de la fuerza o trabajo entre dos puntos cualquiera del espacio sea independiente del camino • …que la circulación de la fuerza en cualquier camino cerrado sea nula



La fuerza es conservativa

Si la energía potencial es una función que depende de una sola coordenada podemos obtener abundante información sobre el sistema a partir de su estudio

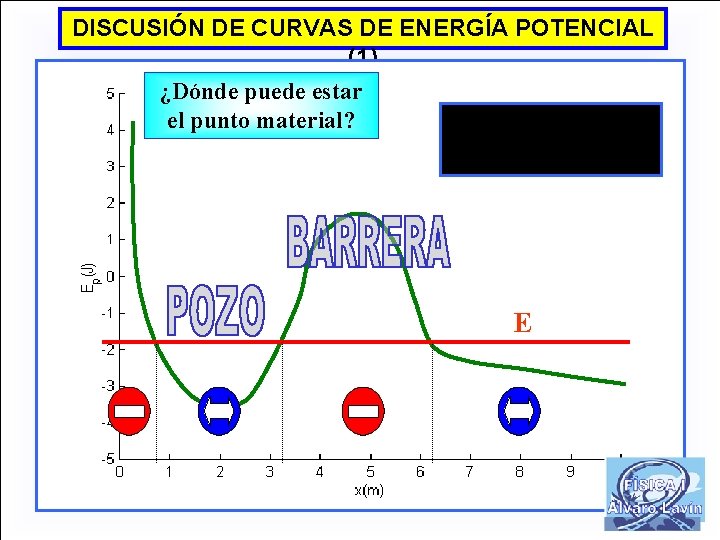
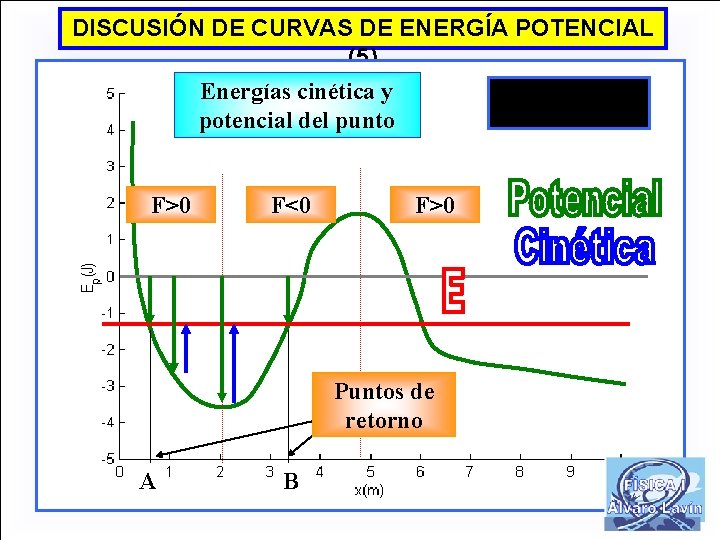
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (1) ¿Dónde puede estar el punto material? E

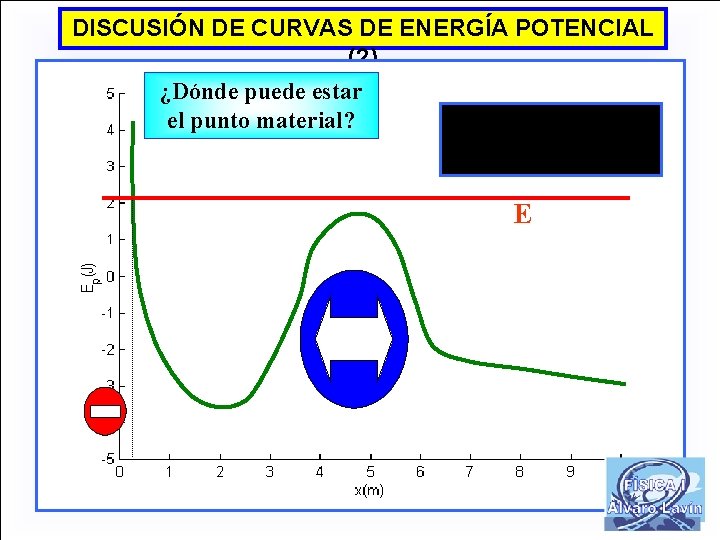
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (2) ¿Dónde puede estar el punto material? E

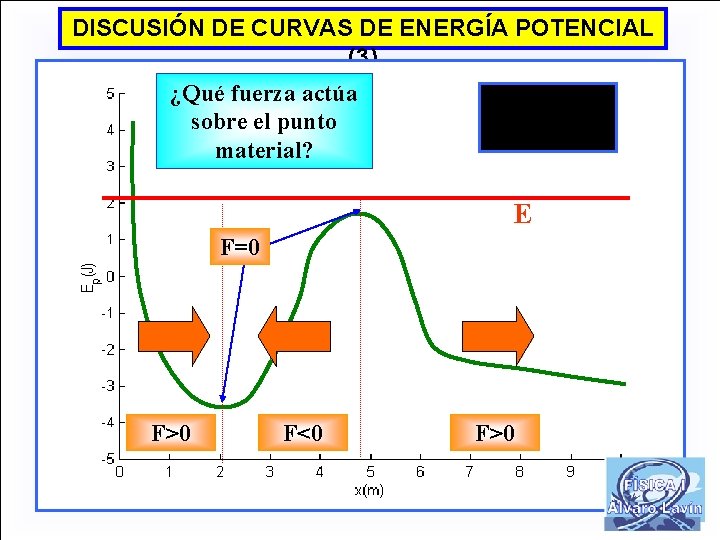
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (3) ¿Qué fuerza actúa sobre el punto material? E F=0 F>0 F<0 F>0

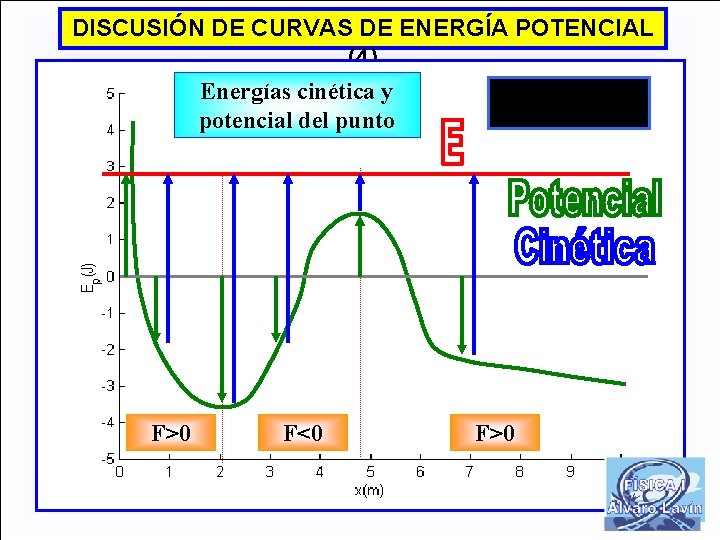
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (4) Energías cinética y potencial del punto F>0 F<0 F>0

DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (5) Energías cinética y potencial del punto F>0 F<0 F>0 Puntos de retorno A B


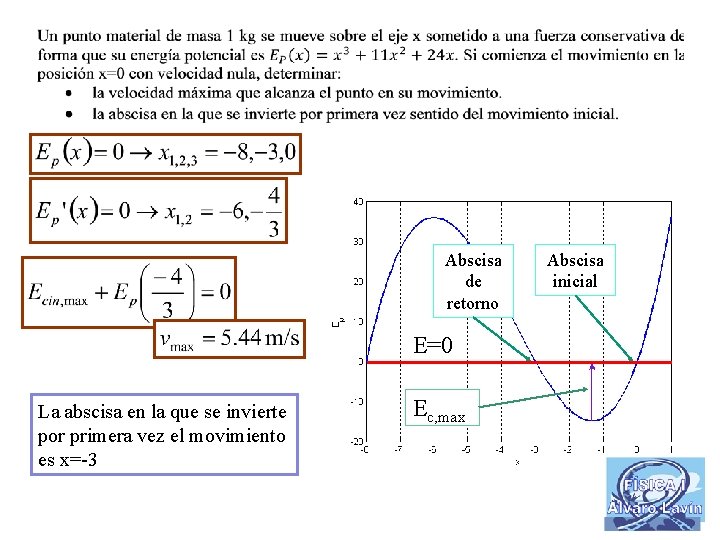
Abscisa de retorno E=0 La abscisa en la que se invierte por primera vez el movimiento es x=-3 Ec, max Abscisa inicial

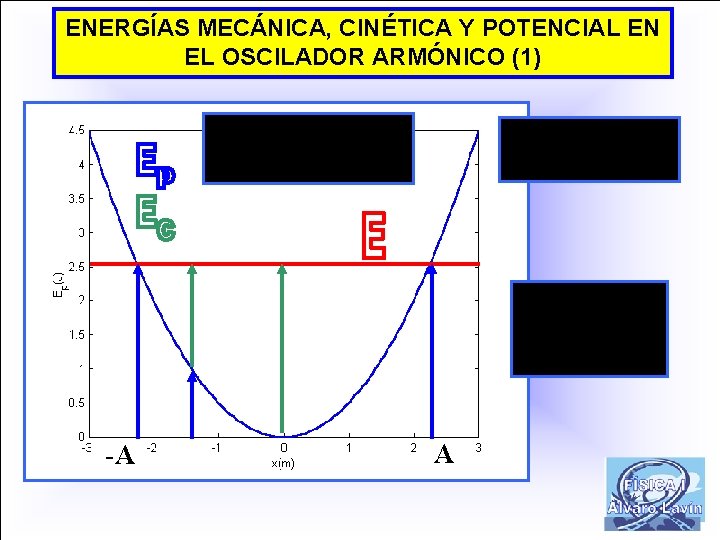
ENERGÍAS MECÁNICA, CINÉTICA Y POTENCIAL EN EL OSCILADOR ARMÓNICO (1) -A A

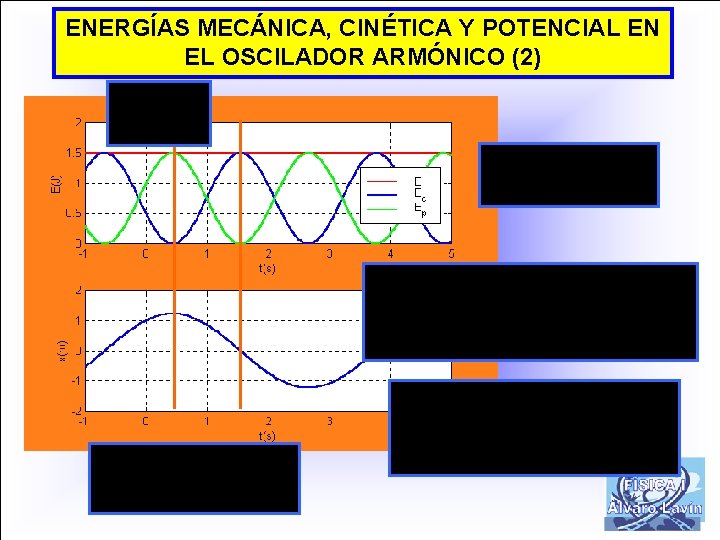
ENERGÍAS MECÁNICA, CINÉTICA Y POTENCIAL EN EL OSCILADOR ARMÓNICO (2)

OSCILACIONES ANARMÓNICAS Serie de Taylor Frecuencia de las pequeñas oscilaciones alrededor de la posición de equilibrio

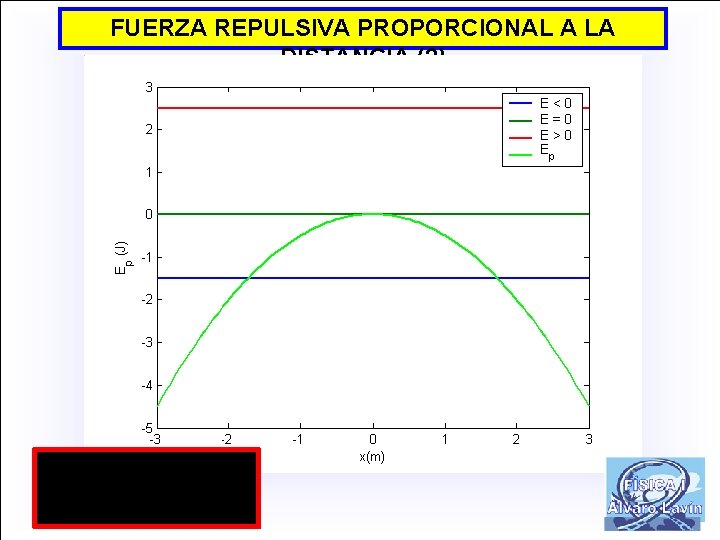
FUERZA REPULSIVA PROPORCIONAL A LA DISTANCIA (1)

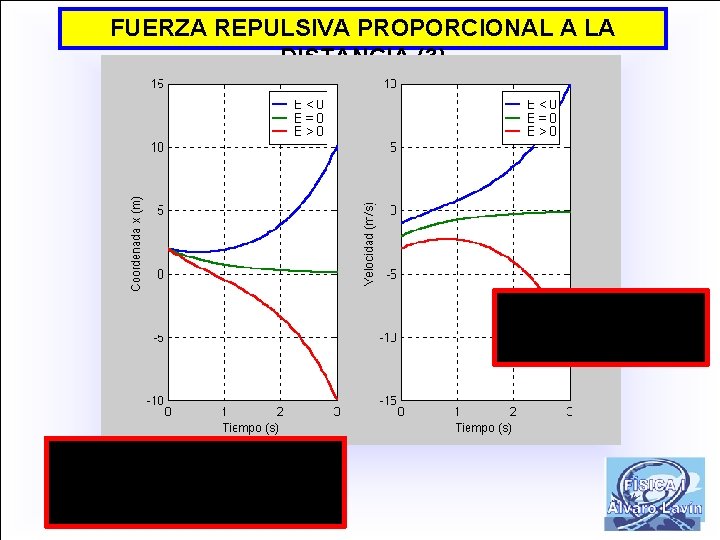
FUERZA REPULSIVA PROPORCIONAL A LA DISTANCIA (2)

FUERZA REPULSIVA PROPORCIONAL A LA DISTANCIA (3)




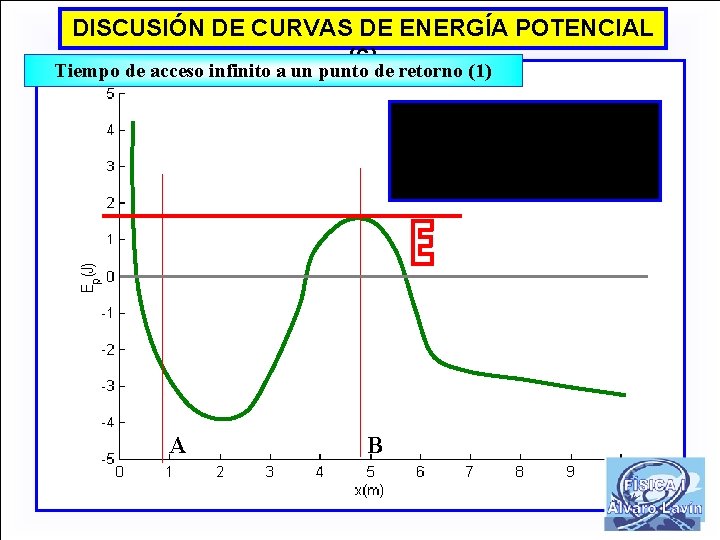
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (6) Tiempo de acceso infinito a un punto de retorno (1) A B

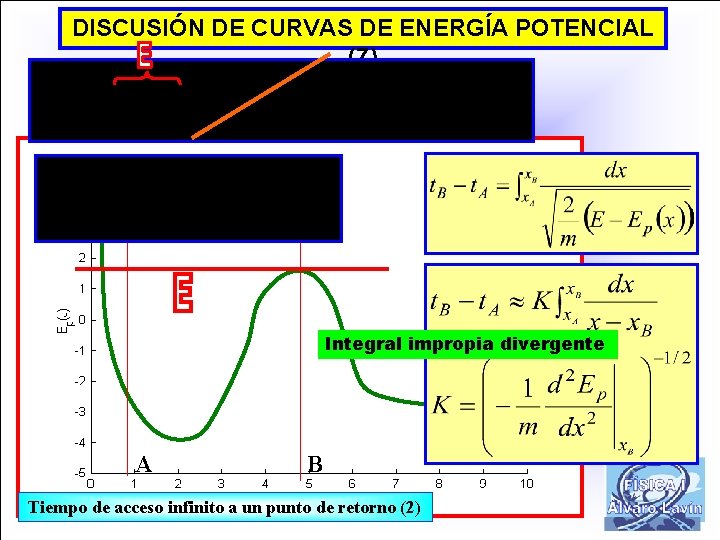
DISCUSIÓN DE CURVAS DE ENERGÍA POTENCIAL (7) Integral impropia divergente A B Tiempo de acceso infinito a un punto de retorno (2)


CAÍDA DE UN OBJETO ESFÉRICO EN UN FLUIDO VISCOSO (1) z=0 k

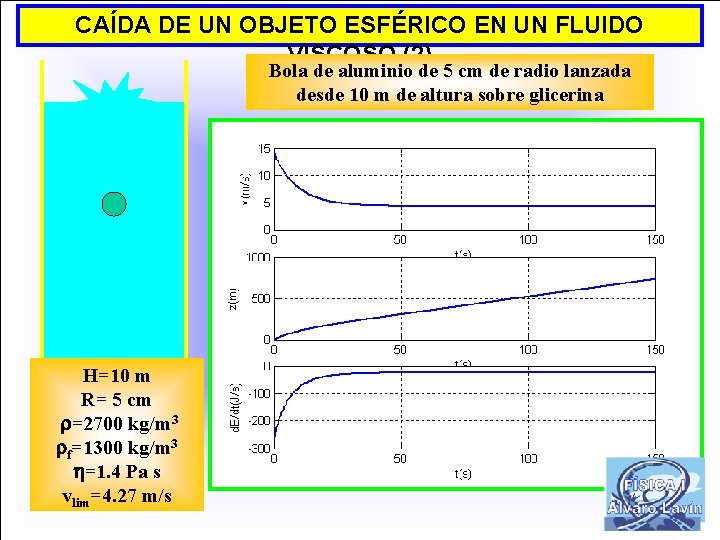
CAÍDA DE UN OBJETO ESFÉRICO EN UN FLUIDO VISCOSO (2) Bola de aluminio de 5 cm de radio lanzada desde 10 m de altura sobre glicerina H=10 m R= 5 cm =2700 kg/m 3 f=1300 kg/m 3 =1. 4 Pa s vlim=4. 27 m/s

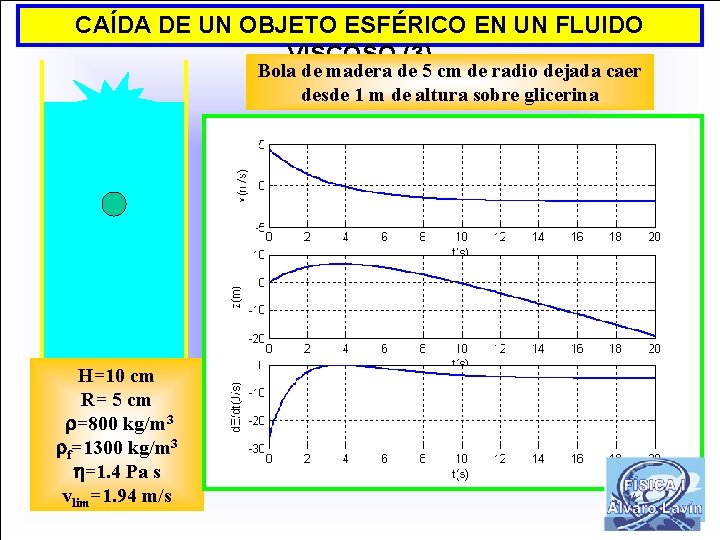
CAÍDA DE UN OBJETO ESFÉRICO EN UN FLUIDO VISCOSO (3) Bola de madera de 5 cm de radio dejada caer desde 1 m de altura sobre glicerina H=10 cm R= 5 cm =800 kg/m 3 f=1300 kg/m 3 =1. 4 Pa s vlim=1. 94 m/s

RESISTENCIA AERODINÁMICA AL AVANCE EN VEHÍCULOS (1)

RESISTENCIA AERODINÁMICA AL AVANCE EN VEHÍCULOS (2)

OSCILADOR AMORTIGUADO (0)

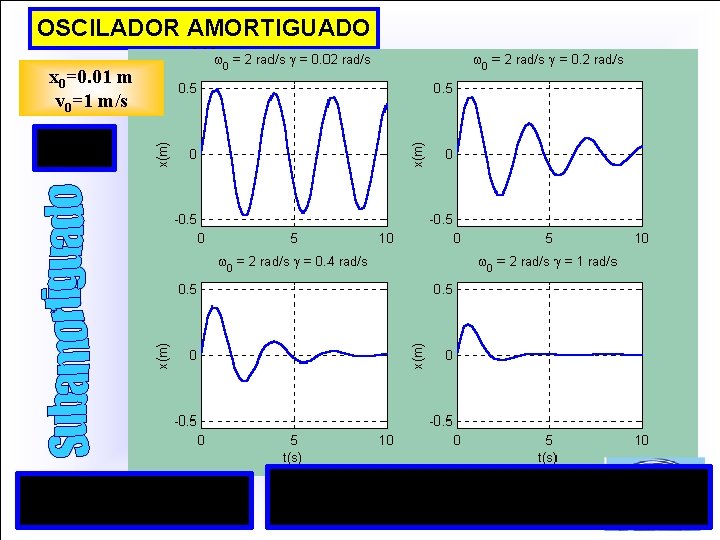
OSCILADOR AMORTIGUADO (1) x 0=0. 01 m v 0=1 m/s

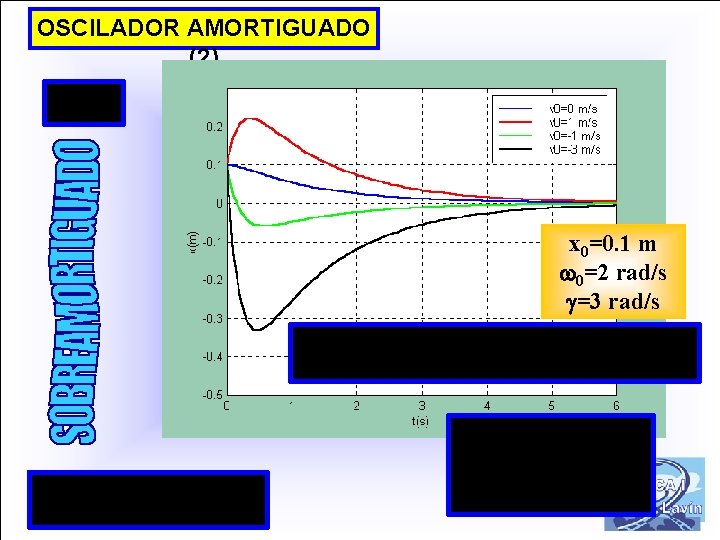
OSCILADOR AMORTIGUADO (2) x 0=0. 1 m 0=2 rad/s =3 rad/s

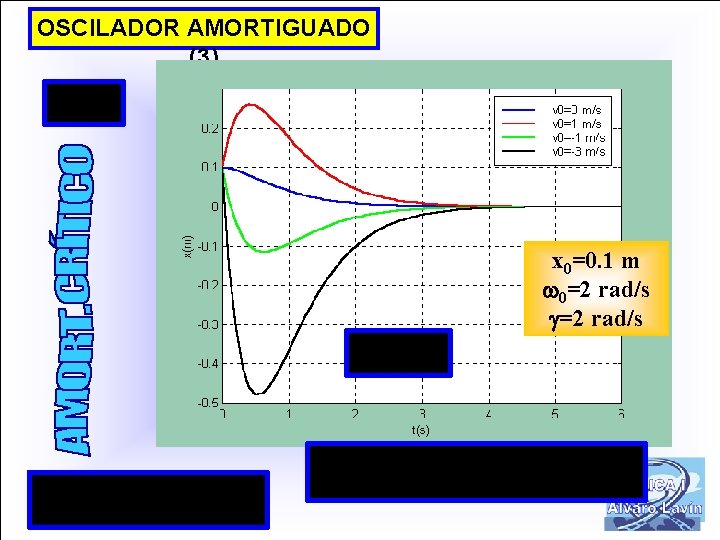
OSCILADOR AMORTIGUADO (3) x 0=0. 1 m 0=2 rad/s

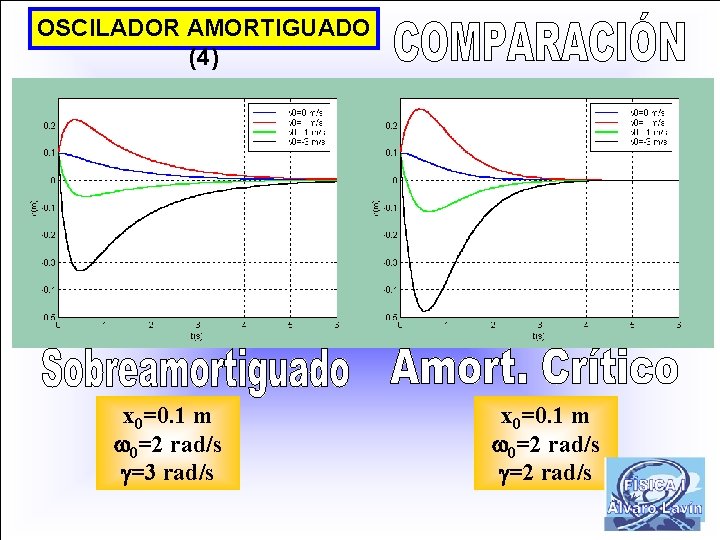
OSCILADOR AMORTIGUADO (4) x 0=0. 1 m 0=2 rad/s =3 rad/s x 0=0. 1 m 0=2 rad/s

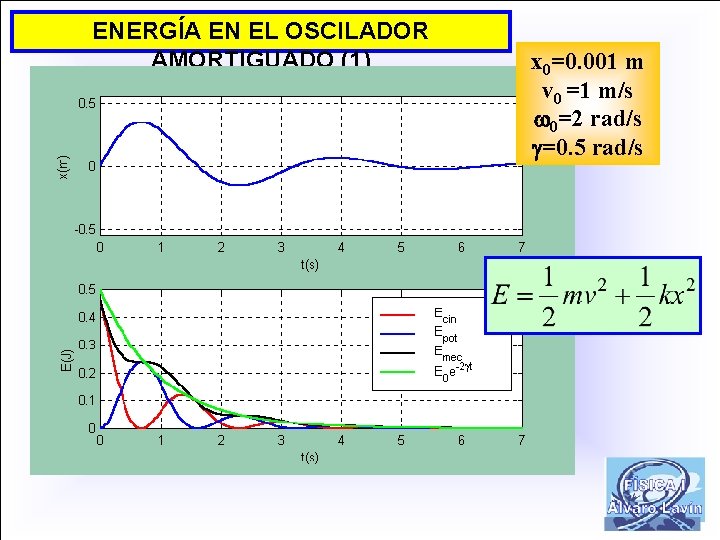
ENERGÍA EN EL OSCILADOR AMORTIGUADO (1) x 0=0. 001 m v 0 =1 m/s 0=2 rad/s =0. 5 rad/s

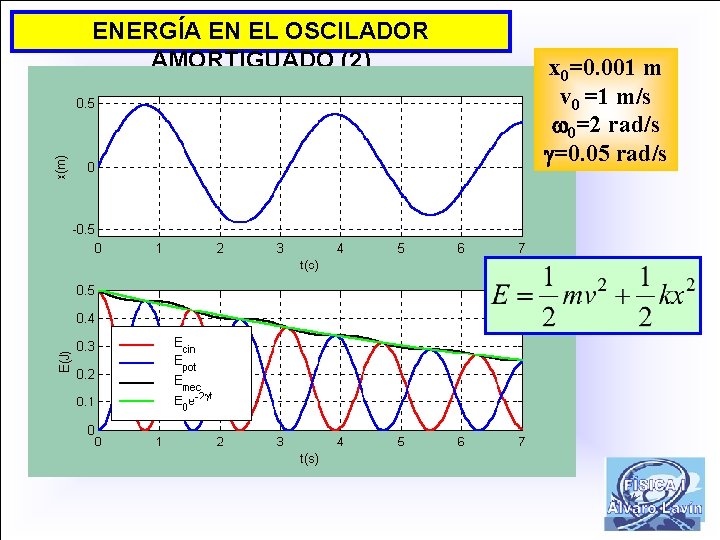
ENERGÍA EN EL OSCILADOR AMORTIGUADO (2) x 0=0. 001 m v 0 =1 m/s 0=2 rad/s =0. 05 rad/s

1 y 2 son reales y negativas

Con los datos del problema 0=2 y =3.

 Tabla de saberes
Tabla de saberes O que dinamica
O que dinamica Dinmica
Dinmica Dinmica
Dinmica Dinmica
Dinmica Puntos coersivos
Puntos coersivos Uso de la coma ejemplos
Uso de la coma ejemplos Flujo luminoso total formula
Flujo luminoso total formula Rete punto punto
Rete punto punto Rete punto a punto
Rete punto a punto Formula centripeta
Formula centripeta Fsica
Fsica Fsica
Fsica Produto escalar
Produto escalar Eficiencia de carnot
Eficiencia de carnot Reacciones estatica
Reacciones estatica Lógica
Lógica Fsica
Fsica Movimento retardado
Movimento retardado Movimento uniforme
Movimento uniforme Ed
Ed Grandezas fisicas
Grandezas fisicas Vaviao
Vaviao Vectores unitarios
Vectores unitarios Leis de newton
Leis de newton Fsica
Fsica Aceleración centrípeta o radial
Aceleración centrípeta o radial Fsica
Fsica Fsica
Fsica Vector resultante
Vector resultante Fsica
Fsica Fsica
Fsica Electrostática ejemplos
Electrostática ejemplos Resolução
Resolução Punto medio
Punto medio Elementos exteriores del punto de venta
Elementos exteriores del punto de venta Cinematica del punto materiale
Cinematica del punto materiale Ejercicios con la r y rr
Ejercicios con la r y rr Dacriolitis
Dacriolitis Parrafo con signos de interrogacion y exclamacion
Parrafo con signos de interrogacion y exclamacion Coma hiperbatica
Coma hiperbatica Concordancia
Concordancia Metodo del punto medio economia
Metodo del punto medio economia Per un punto del piano passano infinite rette e
Per un punto del piano passano infinite rette e Representacion grafica punto muerto
Representacion grafica punto muerto Objetivo general del ciclo del agua
Objetivo general del ciclo del agua Signo por
Signo por Diferencia entre gran plano general y plano general
Diferencia entre gran plano general y plano general Where did general lee surrender to general grant?
Where did general lee surrender to general grant? Producto escalar de vectores
Producto escalar de vectores Determinar el momento de fuerza con respecto al punto o
Determinar el momento de fuerza con respecto al punto o Aminoácidos esenciales
Aminoácidos esenciales Punto homologo
Punto homologo Hallar la distancia entre las palmeras b y c
Hallar la distancia entre las palmeras b y c Punto igual presion
Punto igual presion Propiedades del xenón
Propiedades del xenón Cuando se usa punto y seguido
Cuando se usa punto y seguido Signos para enumerar
Signos para enumerar Punto rojo overlay
Punto rojo overlay Maniobra de adams
Maniobra de adams Fonetica definicion
Fonetica definicion Andamio de un punto
Andamio de un punto Cual es la pendiente de una recta horizontal
Cual es la pendiente de una recta horizontal Números de punto fijo
Números de punto fijo Punto de equilibrio multiproducto
Punto de equilibrio multiproducto Punti notevoli di un triangolo isoscele
Punti notevoli di un triangolo isoscele Como localizarias un lugar en la superficie terrestre
Como localizarias un lugar en la superficie terrestre Como se localiza un punto en la superficie terrestre
Como se localiza un punto en la superficie terrestre La esquina integrantes
La esquina integrantes Katangian at anyo ng talumpati
Katangian at anyo ng talumpati Punto simple con nudo enterrado o invertido
Punto simple con nudo enterrado o invertido Por donde sale el sol
Por donde sale el sol L'equilibrio dei solidi
L'equilibrio dei solidi Disequazioni in due variabili
Disequazioni in due variabili 1 mol
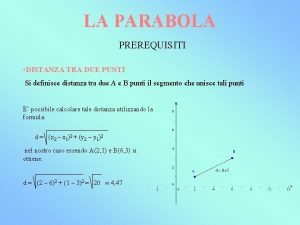
1 mol Distanza punto parabola
Distanza punto parabola Coefficiente di correlazione
Coefficiente di correlazione Las consonantes continuas son
Las consonantes continuas son Propiedad de la tangente a una circunferencia
Propiedad de la tangente a una circunferencia Onda r
Onda r Macchine semplici zanichelli
Macchine semplici zanichelli Variabili reali economia
Variabili reali economia Escala daniel
Escala daniel Punto final definicion
Punto final definicion Punto j en electrocardiograma
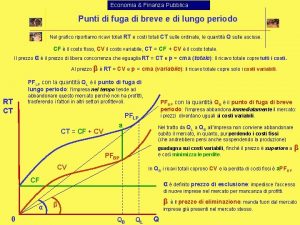
Punto j en electrocardiograma Punto di fuga economia
Punto di fuga economia Punto isosbestico
Punto isosbestico Dame un punto de apoyo
Dame un punto de apoyo Distanza punto retta
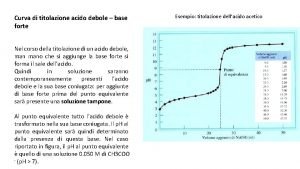
Distanza punto retta Titolazione base forte acido debole
Titolazione base forte acido debole Punto continuo simple
Punto continuo simple Punto subastrale
Punto subastrale Partes de un comentario de texto
Partes de un comentario de texto Exterior interior y frontera
Exterior interior y frontera Notación de punto flotante
Notación de punto flotante Scomposizione forze piano inclinato
Scomposizione forze piano inclinato Maniobra de talopercusión
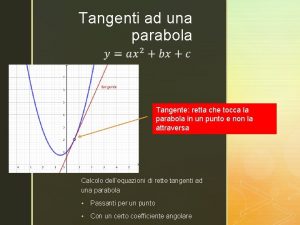
Maniobra de talopercusión Tangenza retta parabola
Tangenza retta parabola Punto della situazione significato
Punto della situazione significato Klaster halimbawa
Klaster halimbawa Temperatura eutettoidica
Temperatura eutettoidica Aceleración centrípeta
Aceleración centrípeta Messa a punto
Messa a punto Paragraf girintisi ayarlama
Paragraf girintisi ayarlama Isquemia
Isquemia Ejemplo de acido carboxilico
Ejemplo de acido carboxilico Flúor alcalino
Flúor alcalino Calcolo pendenza
Calcolo pendenza