Dinmica de los Sistemas Versin Junio de 2019

Dinámica de los Sistemas Versión: Junio de 2019 1

FÍSICA GENERAL I Tema 11: Dinámica de los sistemas I Tema 1: Magnitudes físicas. Unidades y medidas Sistemas materiales. Fuerzas interiores y exteriores. Tema 2: Vectores y sistemas de vectores Magnitudes cinéticas y teoremas fundamentales en sistemas de referencia inerciales Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 5: Cinemática del sólido rígido Tema 6: Cinemática relativa del punto Tema 7: Dinámica del punto Sistema centro de masas: teoremas de Koenig Teoremas fundamentales de la dinámica de sistemas en el sistema centro de masas Colisiones Tema 12: Dinámica de los sistemas II Tema 8: Trabajo y energía I Momentos de inercia centrales, áxicos y planarios. Relaciones entre ellos. Tema 9: Trabajo y energía II Teoremas de Steiner Tema 10: Movimiento del punto bajo fuerzas centrales Aplicación de los teoremas fundamentales de la dinámica: Tema 11: Dinámica de los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II • Traslación • Rotación con eje fijo • Rodadura Análisis alternativo de aplicaciones utilizando el análisis energético y el sistema centro de masas 2

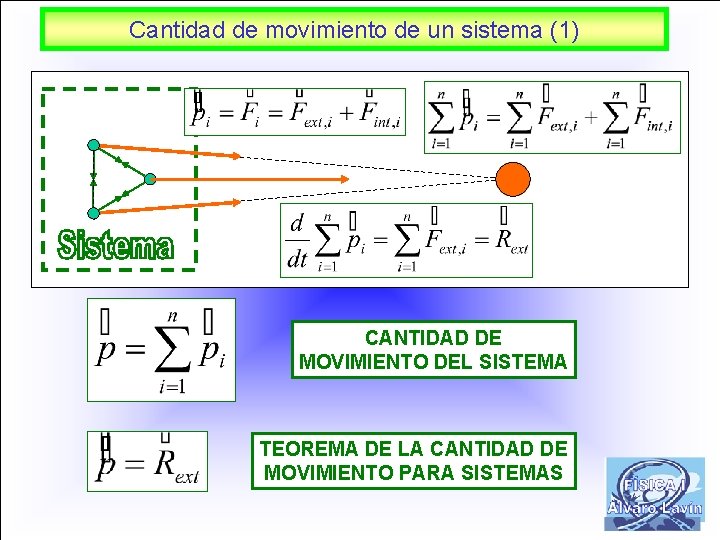
Cantidad de movimiento de un sistema (1) CANTIDAD DE MOVIMIENTO DEL SISTEMA TEOREMA DE LA CANTIDAD DE MOVIMIENTO PARA SISTEMAS 3

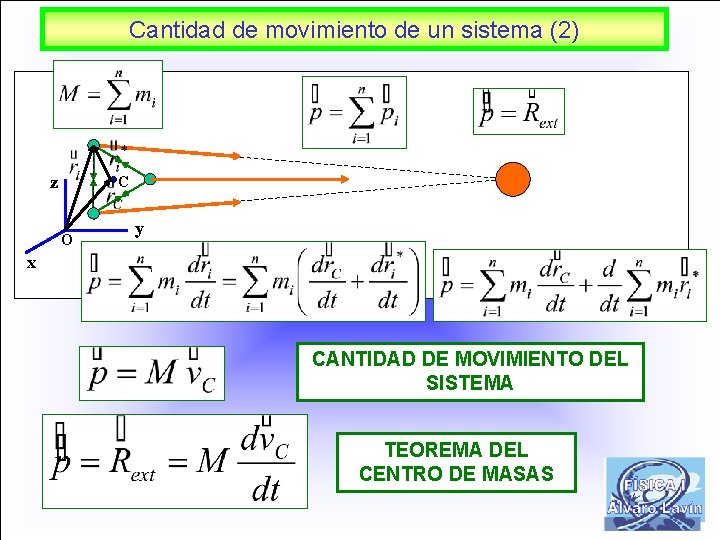
Cantidad de movimiento de un sistema (2) z C O y x CANTIDAD DE MOVIMIENTO DEL SISTEMA TEOREMA DEL CENTRO DE MASAS 4

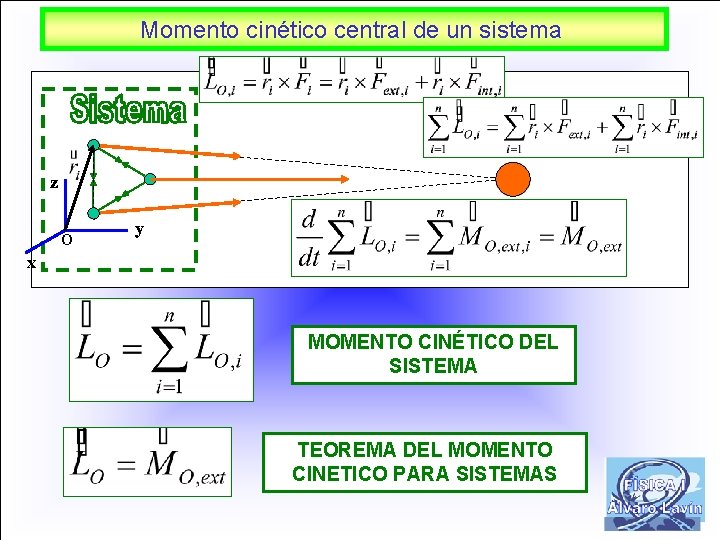
Momento cinético central de un sistema z O y x MOMENTO CINÉTICO DEL SISTEMA TEOREMA DEL MOMENTO CINETICO PARA SISTEMAS 5

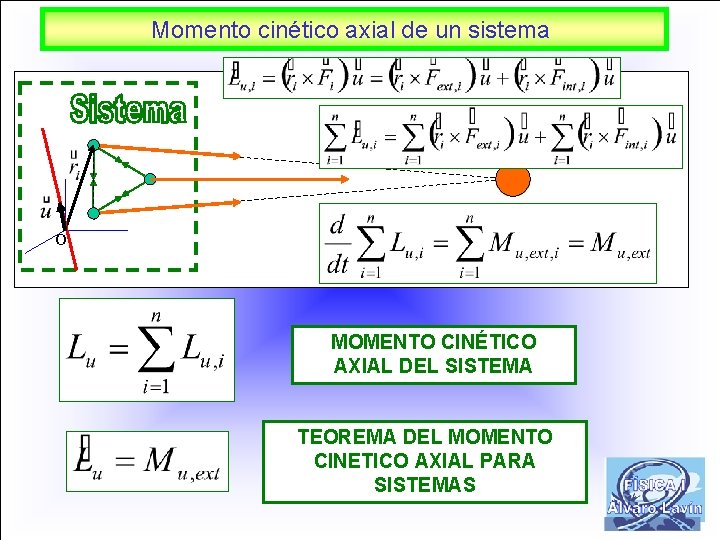
Momento cinético axial de un sistema O MOMENTO CINÉTICO AXIAL DEL SISTEMA TEOREMA DEL MOMENTO CINETICO AXIAL PARA SISTEMAS 6

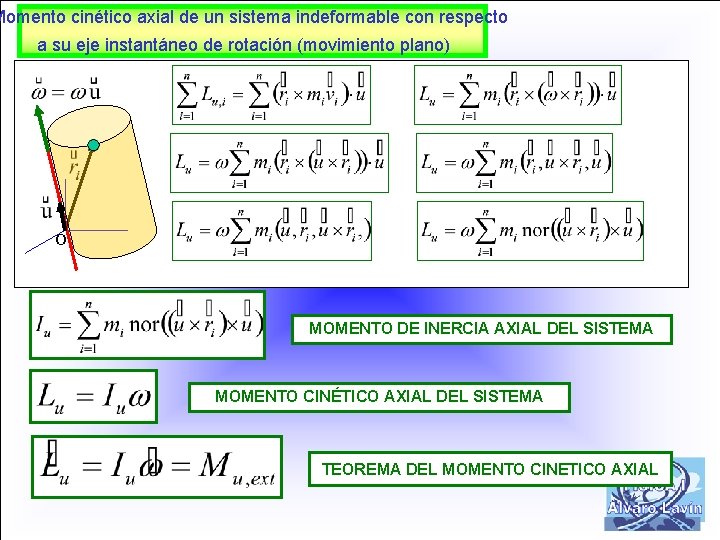
Momento cinético axial de un sistema indeformable con respecto a su eje instantáneo de rotación (movimiento plano) O MOMENTO DE INERCIA AXIAL DEL SISTEMA MOMENTO CINÉTICO AXIAL DEL SISTEMA TEOREMA DEL MOMENTO CINETICO AXIAL 7

R dm 8

9

El balón de playa de la figura tiene una masa total M y un radio R. Calcule: • Su momento de inercia con respecto a un eje que pase por su centro de masas • Su momento de inercia con respecto a un eje tangente a la superficie del balón en un punto

La varilla de la figura tiene longitud total L y está compuesta por dos segmentos de igual longitud L/2 pero densidades lineales diferentes λ 0 y 2 λ 0. Calcule la masa total M de la varilla, la distancia d. C a la que se encuentra el centro de masas del punto A y el momento de inercia de la varilla con respecto a un eje δ perpendicular a la misma que pasa por A

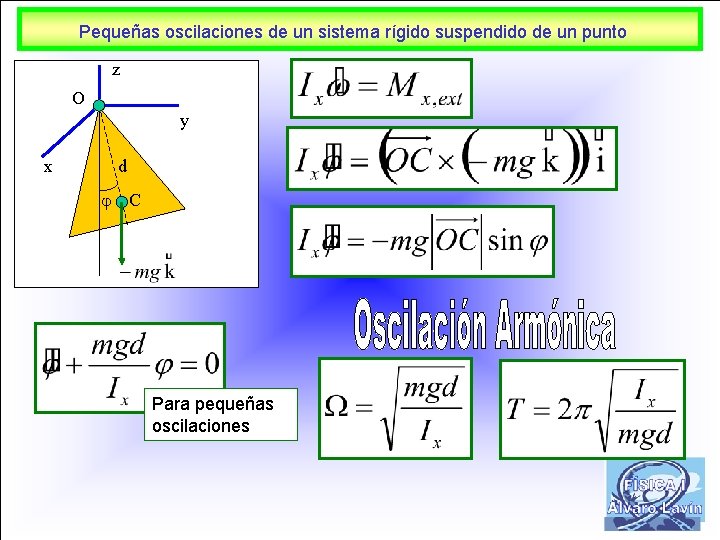
Pequeñas oscilaciones de un sistema rígido suspendido de un punto z O y x d C Para pequeñas oscilaciones 14

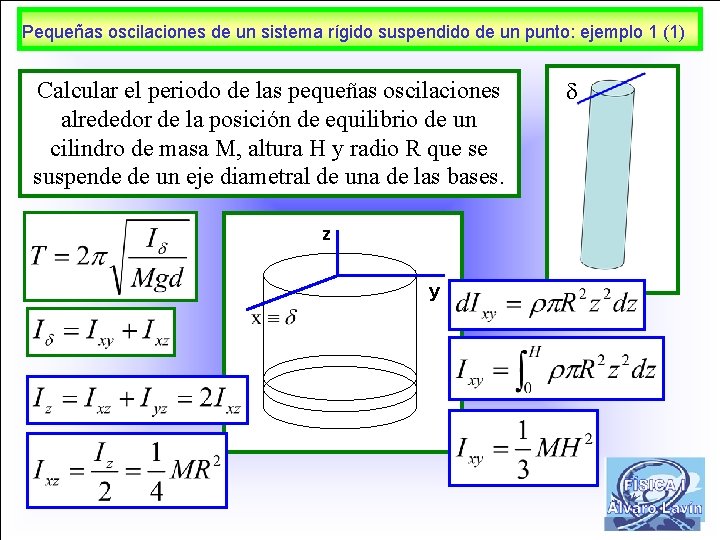
Pequeñas oscilaciones de un sistema rígido suspendido de un punto: ejemplo 1 (1) Calcular el periodo de las pequeñas oscilaciones alrededor de la posición de equilibrio de un cilindro de masa M, altura H y radio R que se suspende de un eje diametral de una de las bases. z y 15

Pequeñas oscilaciones de un sistema rígido suspendido de un punto: ejemplo 1 (2) Calcular el periodo de las pequeñas oscilaciones alrededor de la posición de equilibrio de un cilindro de masa M, altura H y radio R que se suspende de un eje diametral de una de las bases. z y 16

T T

• la aceleración angular en el movimiento de caída • la aceleración de su centro de masas en el movimiento de caída • la tensión de la cuerda Posible solución A 18

FÍSICA GENERAL I Tema 11: Dinámica de los sistemas I Tema 1: Magnitudes físicas. Unidades y medidas Sistemas materiales. Fuerzas interiores y exteriores. Tema 2: Vectores y sistemas de vectores Magnitudes cinéticas y teoremas fundamentales en sistemas de referencia inerciales Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 5: Cinemática del sólido rígido Tema 6: Cinemática relativa del punto Tema 7: Dinámica del punto Sistema centro de masas: teoremas de Koenig Teoremas fundamentales de la dinámica de sistemas en el sistema centro de masas Colisiones Tema 12: Dinámica de los sistemas II Tema 8: Trabajo y energía I Momentos de inercia centrales, áxicos y planarios. Relaciones entre ellos. Tema 9: Trabajo y energía II Teoremas de Steiner Tema 10: Movimiento del punto bajo fuerzas centrales Aplicación de los teoremas fundamentales de la dinámica: Tema 11: Dinámica del los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II • Traslación • Rotación con eje fijo • Rodadura Análisis alternativo de aplicaciones utilizando el análisis energético y el sistema centro de masas 19

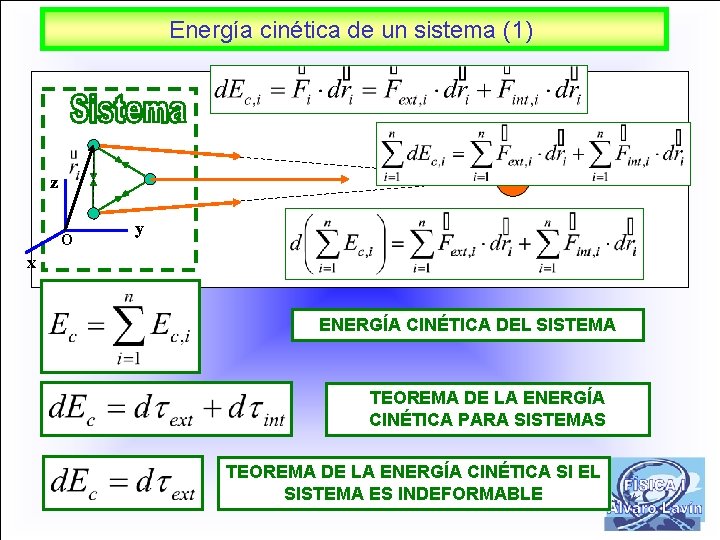
Energía cinética de un sistema (1) z O y x ENERGÍA CINÉTICA DEL SISTEMA TEOREMA DE LA ENERGÍA CINÉTICA PARA SISTEMAS TEOREMA DE LA ENERGÍA CINÉTICA SI EL SISTEMA ES INDEFORMABLE 20

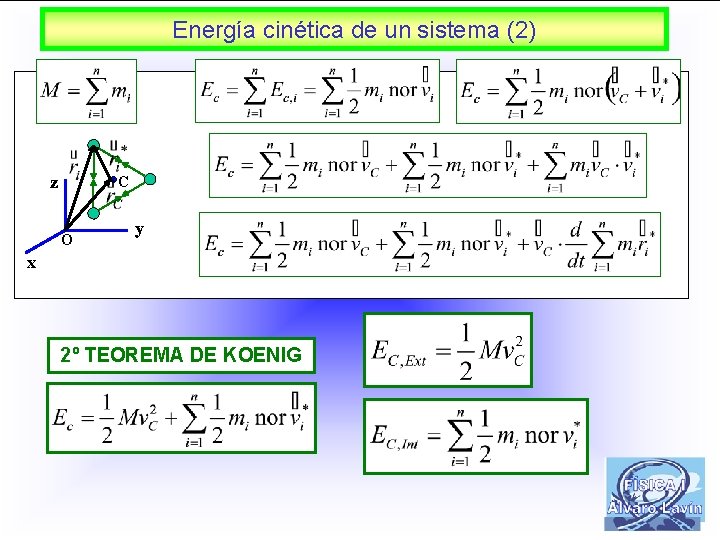
Energía cinética de un sistema (2) z C O y x 2º TEOREMA DE KOENIG 21

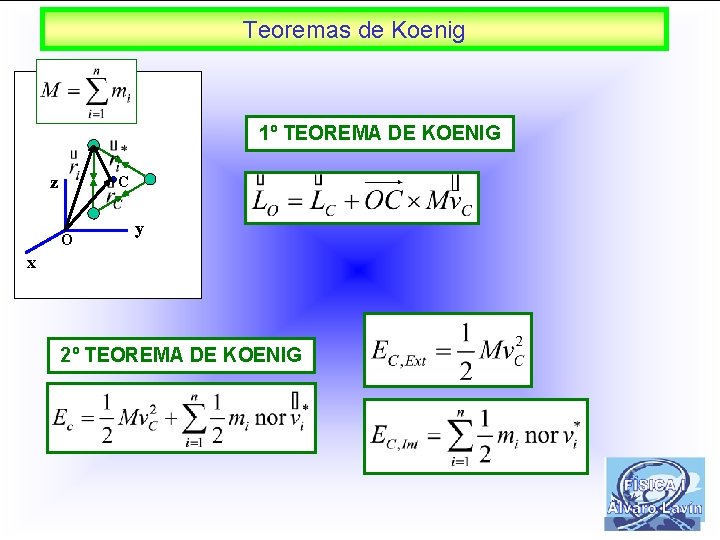
Teoremas de Koenig 1º TEOREMA DE KOENIG z C O y x 2º TEOREMA DE KOENIG 22

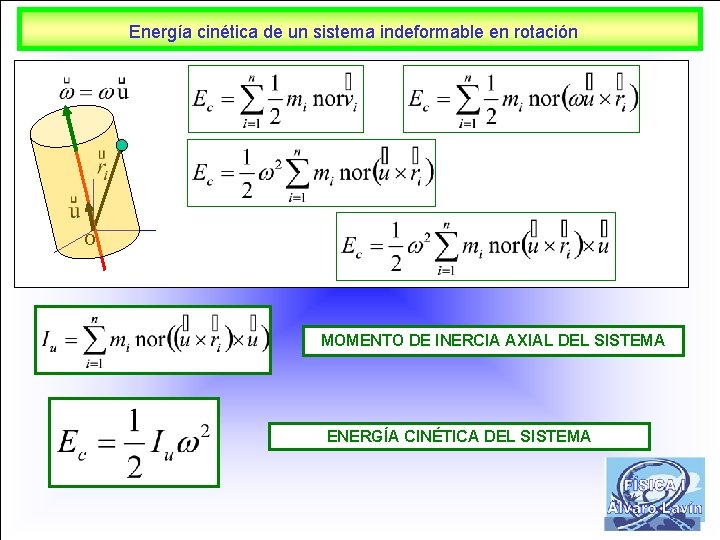
Energía cinética de un sistema indeformable en rotación O MOMENTO DE INERCIA AXIAL DEL SISTEMA ENERGÍA CINÉTICA DEL SISTEMA 23

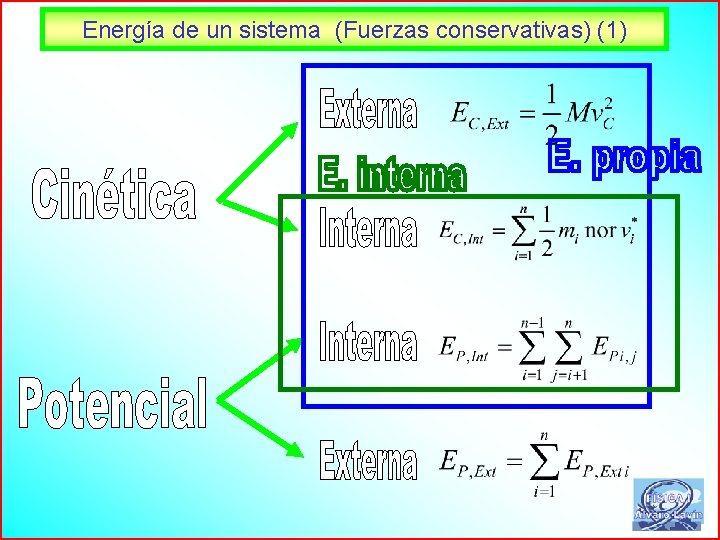
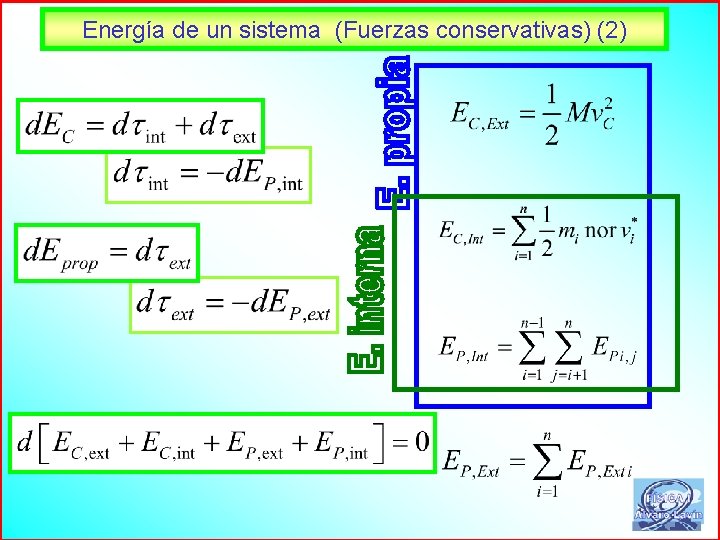
Energía de un sistema (Fuerzas conservativas) (1) 24

Energía de un sistema (Fuerzas conservativas) (2) 25

Objeto que rueda por un plano inclinado (1) Una tubería de masa m, radio R y espesor despreciable frente al radio desciende rodando por un plano inclinado. Parte del reposo y su centro de masas desciende una altura H. Calcular la velocidad del centro de masas cuando ha descendido una altura H. 26

Objeto que rueda por un plano inclinado (2) Una tubería de masa m, radio R y espesor despreciable frente al radio desciende rodando por un plano inclinado. Calcular la aceleración angular que experimenta y la aceleración lineal que experimenta su centro de masas. 27

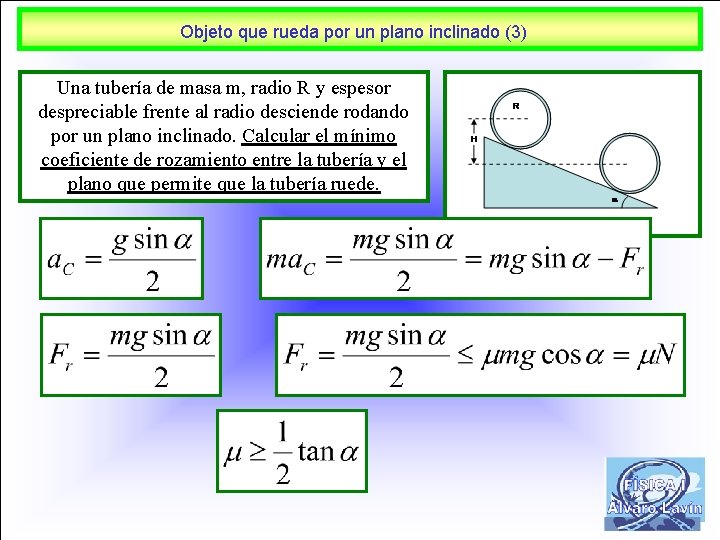
Objeto que rueda por un plano inclinado (3) Una tubería de masa m, radio R y espesor despreciable frente al radio desciende rodando por un plano inclinado. Calcular el mínimo coeficiente de rozamiento entre la tubería y el plano que permite que la tubería ruede. 28

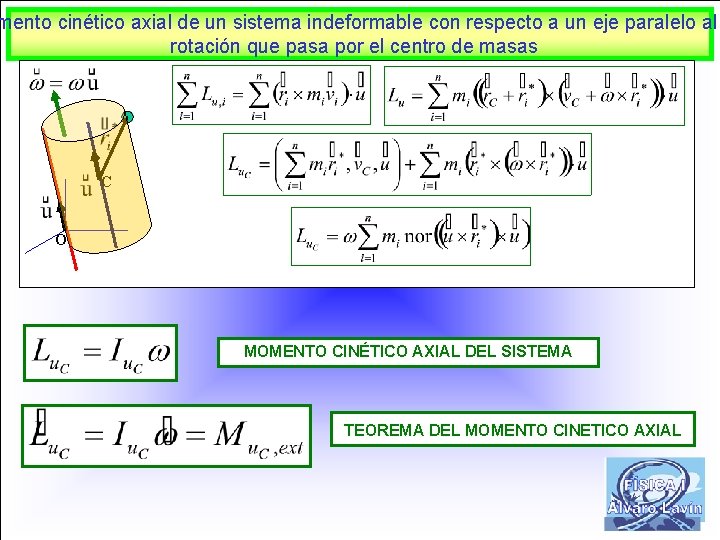
mento cinético axial de un sistema indeformable con respecto a un eje paralelo al rotación que pasa por el centro de masas C O MOMENTO CINÉTICO AXIAL DEL SISTEMA TEOREMA DEL MOMENTO CINETICO AXIAL 29

• la aceleración angular en el movimiento de caída • la aceleración de su centro de masas en el movimiento de caída • la tensión de la cuerda Posible solución B 30

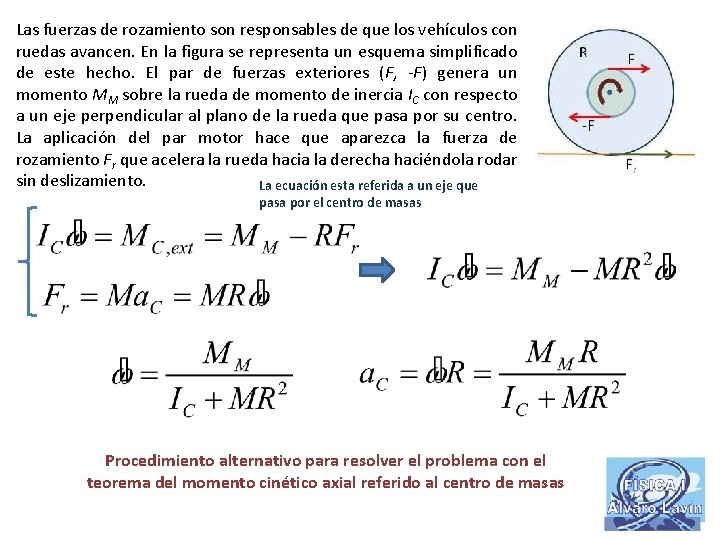
Las fuerzas de rozamiento son responsables de que los vehículos con ruedas avancen. En la figura se representa un esquema simplificado de este hecho. El par de fuerzas exteriores (F, -F) genera un momento MM sobre la rueda de momento de inercia IC con respecto a un eje perpendicular al plano de la rueda que pasa por su centro. La aplicación del par motor hace que aparezca la fuerza de rozamiento Fr que acelera la rueda hacia la derecha haciéndola rodar sin deslizamiento. Calcule: • La aceleración angular que experimenta la rueda y la aceleración de su centro de masas para un valor de MM La ecuación esta referida el eje instantáneo de rotación • La fuerza de rozamiento que se produce para un valor de MM

Las fuerzas de rozamiento son responsables de que los vehículos con ruedas avancen. En la figura se representa un esquema simplificado de este hecho. El par de fuerzas exteriores (F, -F) genera un momento MM sobre la rueda de momento de inercia IC con respecto a un eje perpendicular al plano de la rueda que pasa por su centro. La aplicación del par motor hace que aparezca la fuerza de rozamiento Fr que acelera la rueda hacia la derecha haciéndola rodar sin deslizamiento. Calcule: • El mínimo coeficiente de rozamiento estático entre la rueda y el plano para que la rueda no deslice para un MM dado. (Aunque no están dibujados en la figura, existen un peso de la rueda y una reacción normal del plano)

Las fuerzas de rozamiento son responsables de que los vehículos con ruedas avancen. En la figura se representa un esquema simplificado de este hecho. El par de fuerzas exteriores (F, -F) genera un momento MM sobre la rueda de momento de inercia IC con respecto a un eje perpendicular al plano de la rueda que pasa por su centro. La aplicación del par motor hace que aparezca la fuerza de rozamiento Fr que acelera la rueda hacia la derecha haciéndola rodar sin deslizamiento. La ecuación esta referida a un eje que pasa por el centro de masas Procedimiento alternativo para resolver el problema con el teorema del momento cinético axial referido al centro de masas

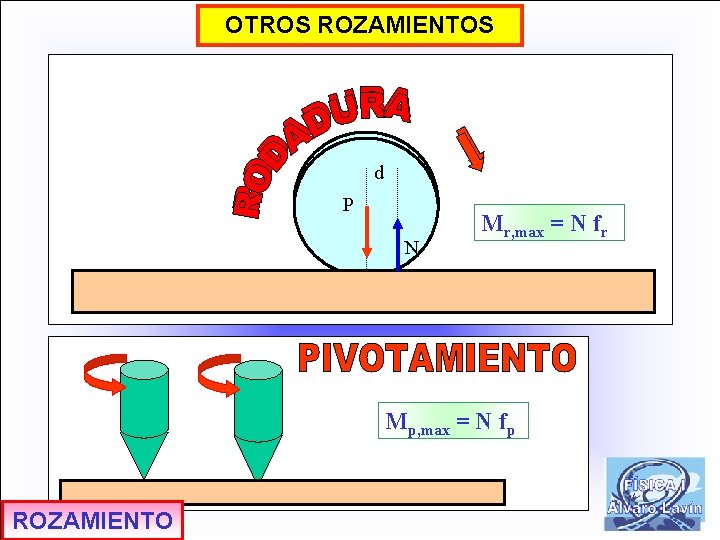
OTROS ROZAMIENTOS d P N Mr, max = N fr Mp, max = N fp ROZAMIENTO

La esfera de densidad uniforme de la figura desciende rodando por un plano inclinado. Parte del reposo y su centro de masas desciende una altura H. El momento de inercia de una esfera con respecto a un eje que pasa por su centro es (2/5)MR 2 Calcular: • La velocidad del centro de masas cuando ha descendido una altura H El primer apartado puede hacerse a partir del principio de conservación de la energía mecánica. Si se aplica el teorema de Koenig para expresar la energía cinética del sistema obtenemos:

La esfera de densidad uniforme de la figura desciende rodando por un plano inclinado. Parte del reposo y su centro de masas desciende una altura H. El momento de inercia de una esfera con respecto a un eje que pasa por su centro es (2/5)MR 2 Calcular: • La aceleración del centro de masas El segundo apartado puede hacerse a partir del teorema del momento cinético axial para sistemas indeformables aplicado en el eje instantáneo de rotación

La esfera de densidad uniforme de la figura desciende rodando por un plano inclinado. Parte del reposo y su centro de masas desciende una altura H. El momento de inercia de una esfera con respecto a un eje que pasa por su centro es (2/5)MR 2 Calcular: • La fuerza de fricción que ejerce el plano sobre la esfera El tercer apartado puede hacerse a partir del teorema del centro de masas Fr M g senα

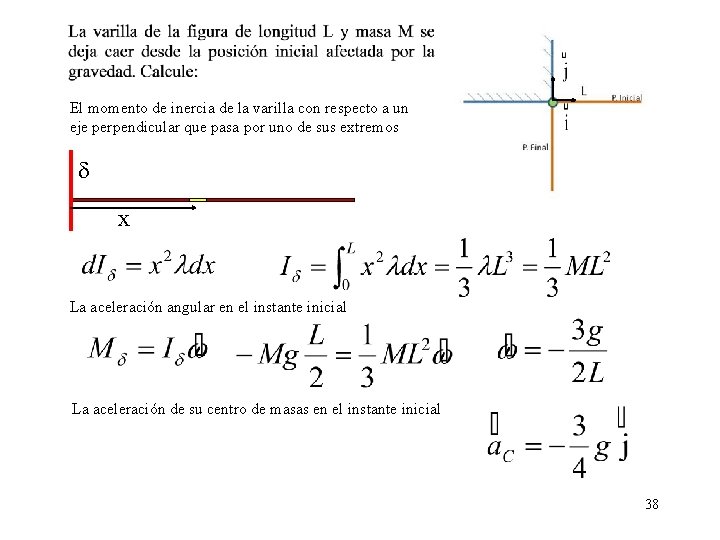
El momento de inercia de la varilla con respecto a un eje perpendicular que pasa por uno de sus extremos x La aceleración angular en el instante inicial La aceleración de su centro de masas en el instante inicial 38

La aceleración de su centro de masas en el instante inicial La reacción en la articulación de la varilla en el instante inicial La velocidad angular de la varilla cuando llega a la posición vertical La velocidad del centro de masas de la varilla cuando llega a la posición vertical 39

La velocidad del centro de masas de la varilla cuando llega a la posición vertical La componente intrínseca de aceleración normal de su centro de masas cuando llega a la posición vertical La reacción en la articulación de la varilla cuando llega a la posición vertical 40

La varilla de la figura tiene longitud total L y está compuesta por dos segmentos de igual longitud L/2 pero densidades lineales diferentes λ 0 y 2 λ 0. Calcule la masa total M de la varilla, la distancia d. C a la que se encuentra el centro de masas del punto A y el momento de inercia de la varilla con respecto a un eje δ perpendicular a la misma que pasa por A

La varilla que se ha estudiado en el ejercicio 3 se coloca en posición horizontal con el extremo A fijo en una articulación que permite su rotación según se indica en la figura. Se abandona la varilla al efecto de la gravedad desde la posición horizontal y ésta alcanza en un instante dado la posición vertical. Se pide calcular para ese instante: • La velocidad angular de la varilla en función de M, d. C, Iδ y g La velocidad angular final de la varilla puede conocerse aplicando el principio de conservación de la energía mecánica del sistema. Considerando que en la posición inicial la varilla tiene energía potencial nula… • La velocidad lineal del centro de masas de la varilla en función de M, d. C, Iδ y g El centro de masas de la varilla describe una trayectoria circunferencial de radio d C

La varilla que se ha estudiado en el ejercicio 3 se coloca en posición horizontal con el extremo A fijo en una articulación que permite su rotación según se indica en la figura. Se abandona la varilla al efecto de la gravedad desde la posición horizontal y ésta alcanza en un instante dado la posición vertical. Se pide calcular para ese instante: • La aceleración del centro de masas en función de M, d. C, Iδ y g El centro de masas de la varilla describe una trayectoria circunferencial de radio d C, por tanto en la posición B está sometido a una aceleración normal a la trayectoria de valor… Esta aceleración es la única que experimenta el centro de masas ya que la aceleración tangencial es nula al ser nulas componentes de las fuerzas en esa dirección • La reacción de la articulación A en función de M, d. C, Iδ y g Aplicando el teorema del centro de masas referido al vector normal a la trayectoria…

La varilla que se ha estudiado en el ejercicio 3 se coloca en posición horizontal con el extremo A fijo en una articulación que permite su rotación según se indica en la figura. Se abandona la varilla al efecto de la gravedad desde la posición horizontal y ésta alcanza en un instante dado la posición vertical. Se pide calcular para ese instante: • Sustituyendo los valores de d. C e Iδ obtenidos en el ejercicio 3, obtenga la velocidad angular de la varilla como función de la variables g y L

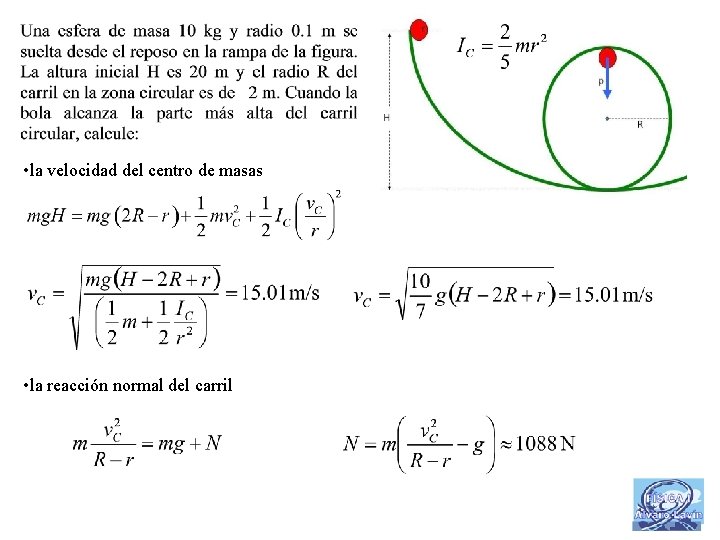
• la velocidad del centro de masas • la reacción normal del carril 45

El momento de inercia del sistema con respecto al eje de rotación. La aceleración angular en el instante inicial. Distancia del CM al eje Masa total La aceleración de su centro de masas en el instante inicial. 46

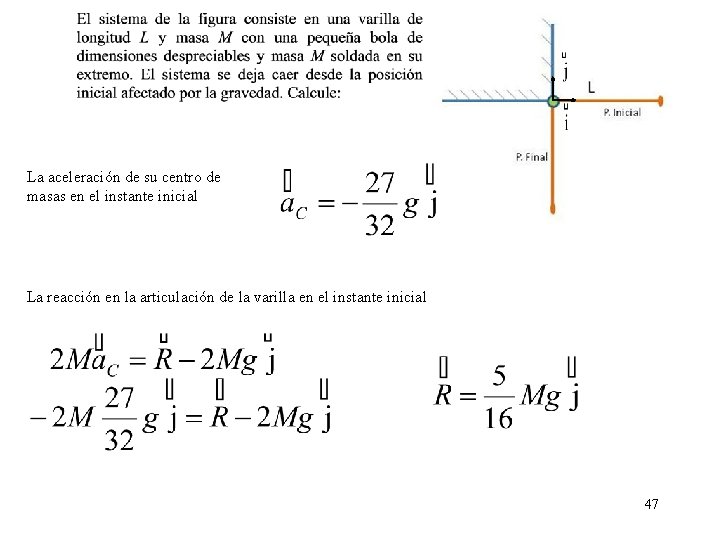
La aceleración de su centro de masas en el instante inicial La reacción en la articulación de la varilla en el instante inicial 47

La velocidad angular de la varilla cuando llega a la posición vertical La velocidad del centro de masas de la varilla cuando llega a la posición vertical 48

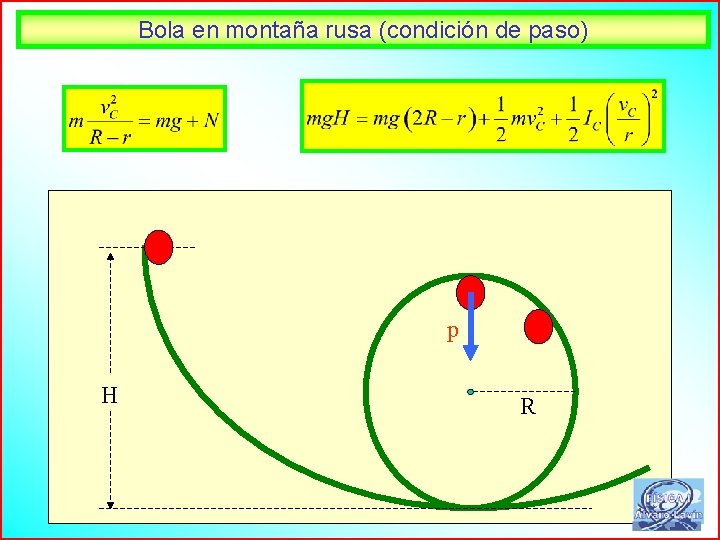
Bola en montaña rusa (condición de paso) p H R 49

Choques en el sistema laboratorio Se conserva la cantidad de movimiento del sistema por no intervenir fuerzas exteriores Se conserva la energía propia del sistema por no haber trabajo de fuerzas exteriores 50

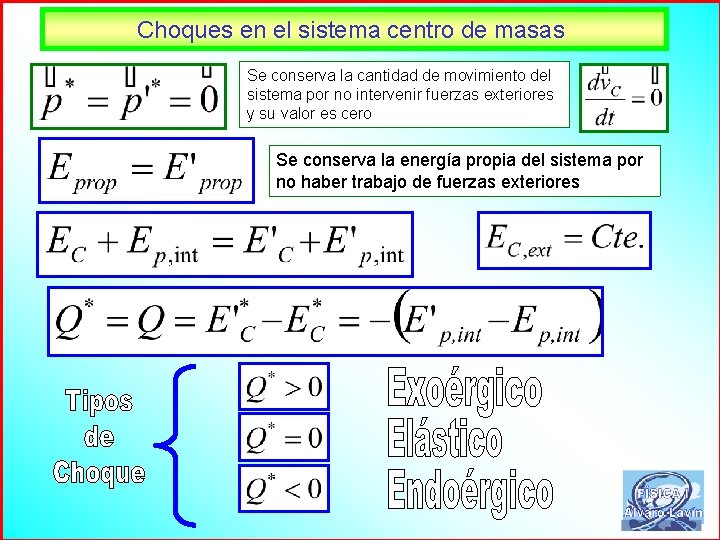
Choques en el sistema centro de masas Se conserva la cantidad de movimiento del sistema por no intervenir fuerzas exteriores y su valor es cero Se conserva la energía propia del sistema por no haber trabajo de fuerzas exteriores 51

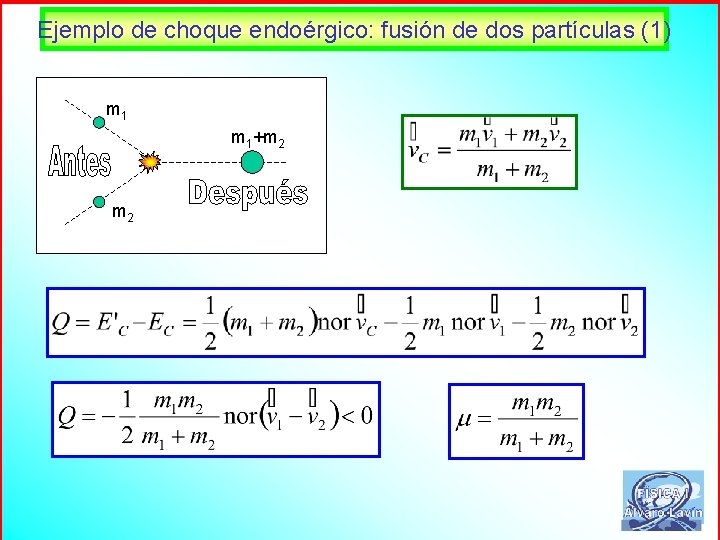
Ejemplo de choque endoérgico: fusión de dos partículas (1) m 1+m 2 52

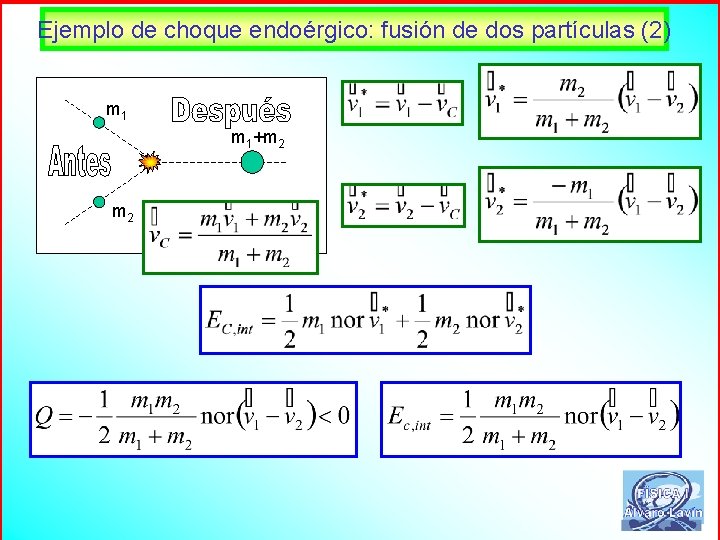
Ejemplo de choque endoérgico: fusión de dos partículas (2) m 1+m 2 53

Un objeto de masa M que se mueve con velocidad v respecto al laboratorio alcanza a un objeto que se mueve en la misma dirección y sentido con velocidad v/2 y que tiene masa 2 M. Tras el choque, los objetos quedan fundidos en un mismo objeto de masa 3 M. Calcular su velocidad. 54

El pato de la figura tiene una masa mp=2 kg y aterriza con velocidad prácticamente horizontal vp=20 m/s sobre un tablón inmóvil de masa mt=20 kg que flota sobre un estanque. El pato resbala sobre el tablón hasta que su velocidad con respecto al mismo se anula. Suponiendo despreciable la fuerza del estanque sobre el tablón, calcule: • La velocidad final del sistema pato-tablón La cantidad de movimiento el sistema formado por el pato y el tablón se conserva por no haber fuerzas exteriores • La variación de energía cinética del sistema pato-tablón 55

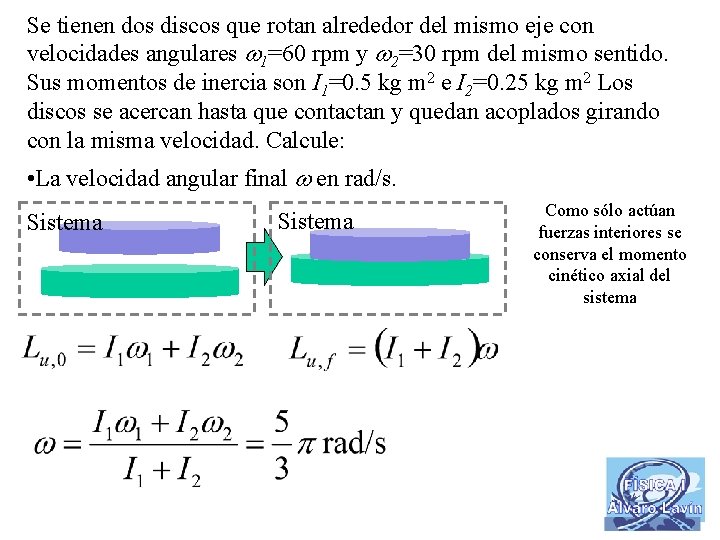
Se tienen dos discos que rotan alrededor del mismo eje con velocidades angulares 1=60 rpm y 2=30 rpm del mismo sentido. Sus momentos de inercia son I 1=0. 5 kg m 2 e I 2=0. 25 kg m 2 Los discos se acercan hasta que contactan y quedan acoplados girando con la misma velocidad. Calcule: • La velocidad angular final en rad/s. Sistema Como sólo actúan fuerzas interiores se conserva el momento cinético axial del sistema

Se tienen dos discos que rotan alrededor del mismo eje con velocidades angulares 1=60 rpm y 2=30 rpm del mismo sentido. Sus momentos de inercia son I 1=0. 5 kg m 2 e I 2=0. 25 kg m 2 Los discos se acercan hasta que contactan y quedan acoplados girando con la misma velocidad. Calcule: • La variación de energía cinética total tras el acoplamiento. Sistema Como sólo actúan fuerzas interiores se conserva el momento cinético axial del sistema

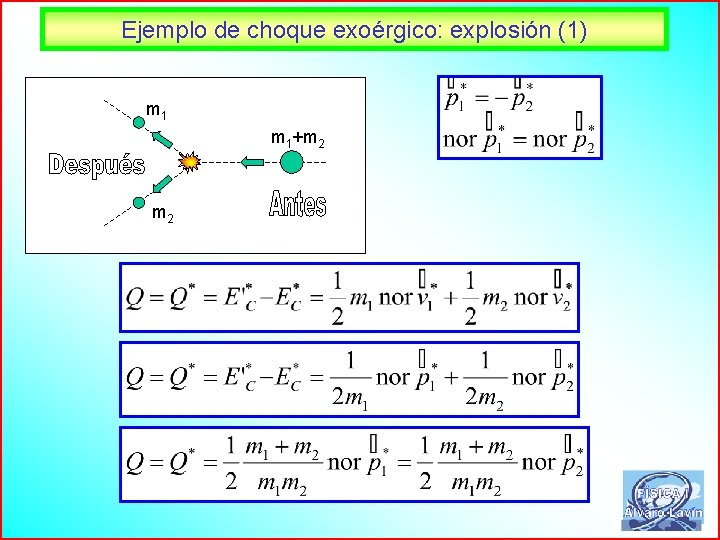
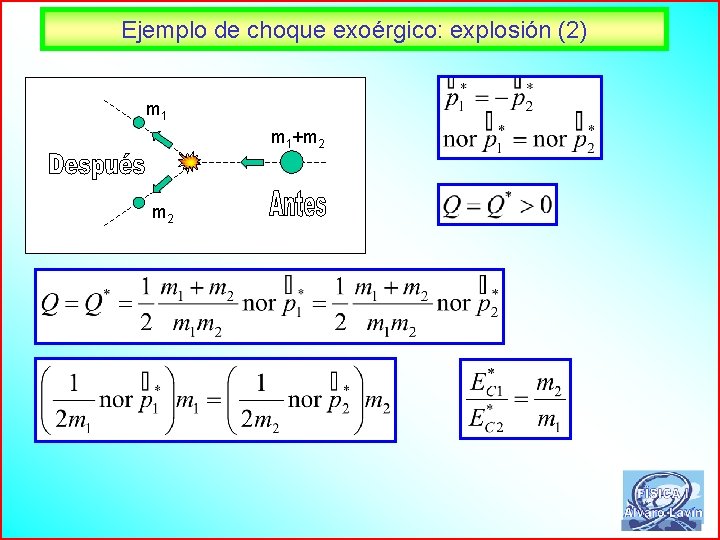
Ejemplo de choque exoérgico: explosión (1) m 1+m 2 58

Ejemplo de choque exoérgico: explosión (2) m 1+m 2 59

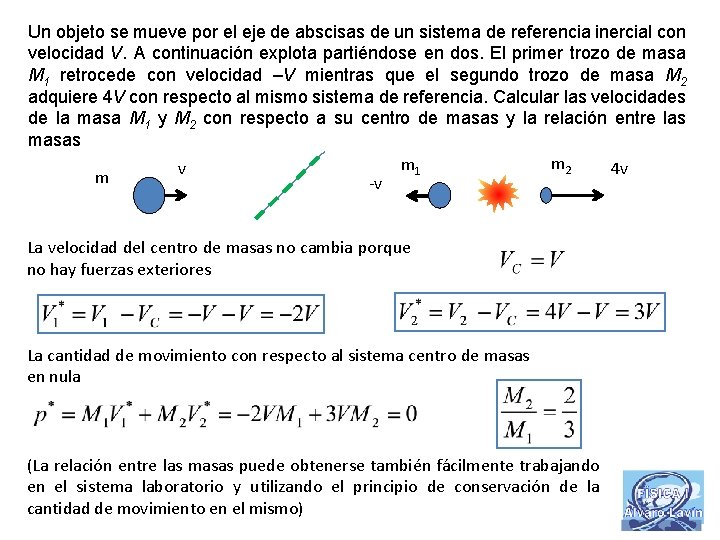
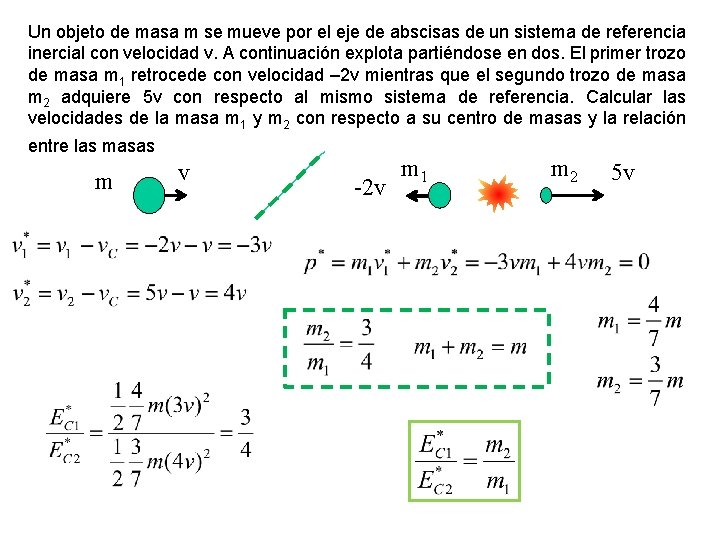
Un objeto se mueve por el eje de abscisas de un sistema de referencia inercial con velocidad V. A continuación explota partiéndose en dos. El primer trozo de masa M 1 retrocede con velocidad –V mientras que el segundo trozo de masa M 2 adquiere 4 V con respecto al mismo sistema de referencia. Calcular las velocidades de la masa M 1 y M 2 con respecto a su centro de masas y la relación entre las masas m 2 m 1 v 4 v m -v La velocidad del centro de masas no cambia porque no hay fuerzas exteriores La cantidad de movimiento con respecto al sistema centro de masas en nula (La relación entre las masas puede obtenerse también fácilmente trabajando en el sistema laboratorio y utilizando el principio de conservación de la cantidad de movimiento en el mismo)

Un objeto de masa m se mueve por el eje de abscisas de un sistema de referencia inercial con velocidad v. A continuación explota partiéndose en dos. El primer trozo de masa m 1 retrocede con velocidad – 2 v mientras que el segundo trozo de masa m 2 adquiere 5 v con respecto al mismo sistema de referencia. Calcular las velocidades de la masa m 1 y m 2 con respecto a su centro de masas y la relación entre las masas m v -2 v m 1 m 2 5 v

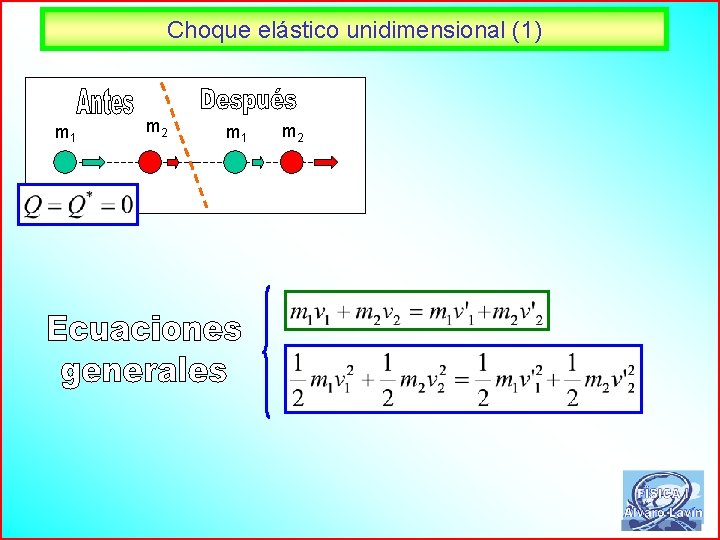
Choque elástico unidimensional (1) m 1 m 2 62

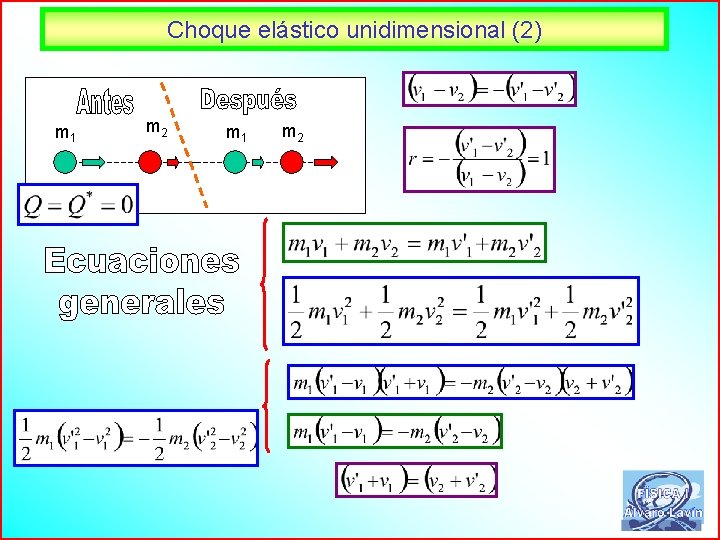
Choque elástico unidimensional (2) m 1 m 2 63

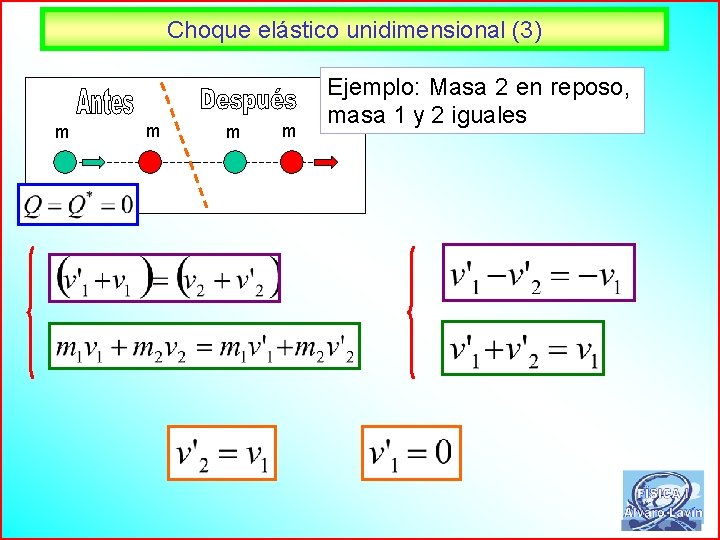
Choque elástico unidimensional (3) m m Ejemplo: Masa 2 en reposo, masa 1 y 2 iguales 64

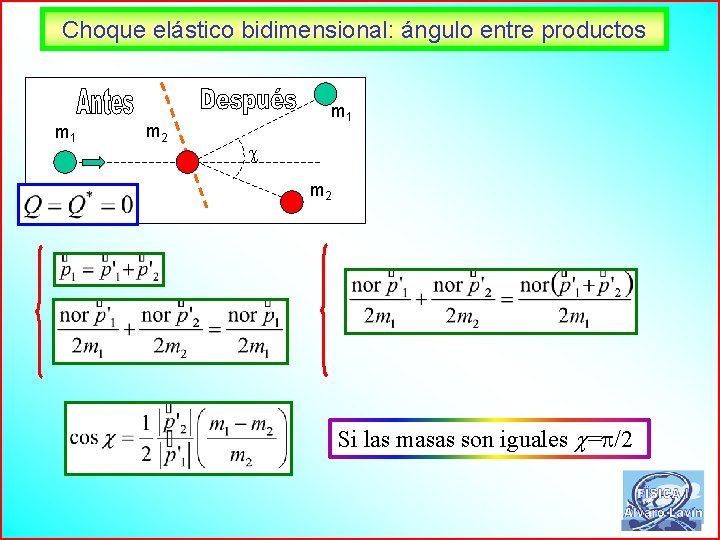
Choque elástico bidimensional: ángulo entre productos m 1 m 2 m 1 m 2 Si las masas son iguales = /2 65

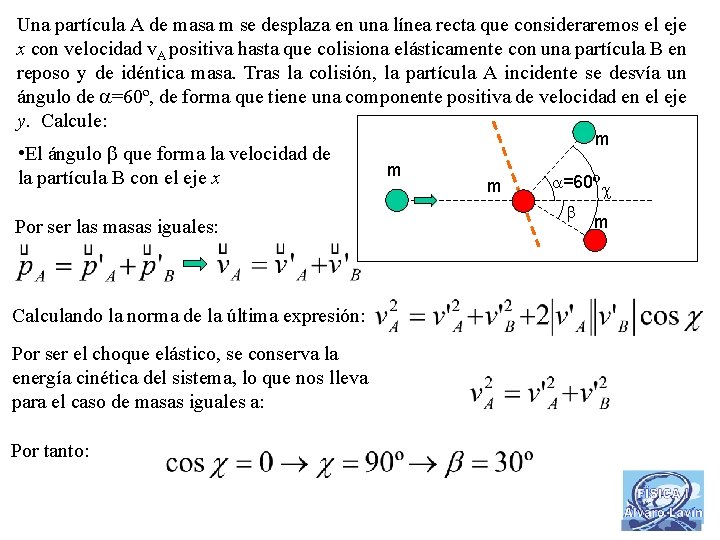
Una partícula A de masa m se desplaza en una línea recta que consideraremos el eje x con velocidad v. A positiva hasta que colisiona elásticamente con una partícula B en reposo y de idéntica masa. Tras la colisión, la partícula A incidente se desvía un ángulo de =60º, de forma que tiene una componente positiva de velocidad en el eje y. Calcule: • El ángulo que forma la velocidad de la partícula B con el eje x Por ser las masas iguales: Calculando la norma de la última expresión: Por ser el choque elástico, se conserva la energía cinética del sistema, lo que nos lleva para el caso de masas iguales a: Por tanto: m m m =60º m

Una partícula A de masa m se desplaza en una línea recta que consideraremos el eje x con velocidad v. A positiva hasta que colisiona elásticamente con una partícula B en reposo y de idéntica masa. Tras la colisión, la partícula A incidente se desvía un ángulo de =60º, de forma que tiene una componente positiva de velocidad en el eje y. Calcule: • Los módulos de las velocidades de las partículas A y B después del choque m m m =60º m 67

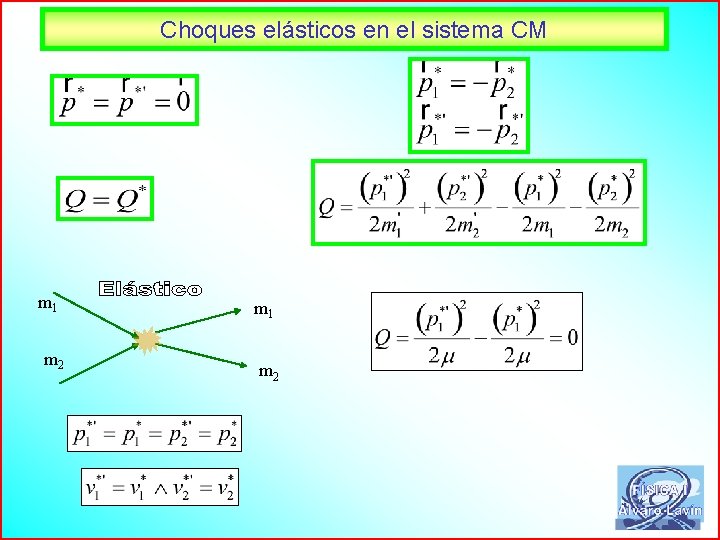
Choques elásticos en el sistema CM m 1 m 2 68

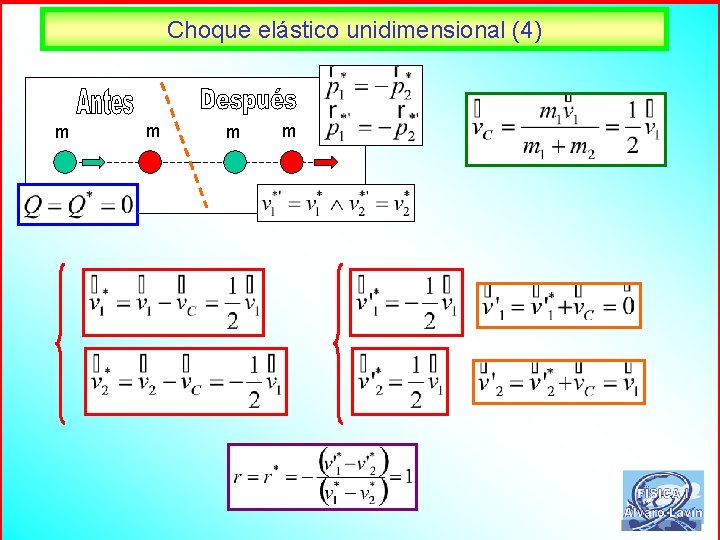
Choque elástico unidimensional (4) m m 69

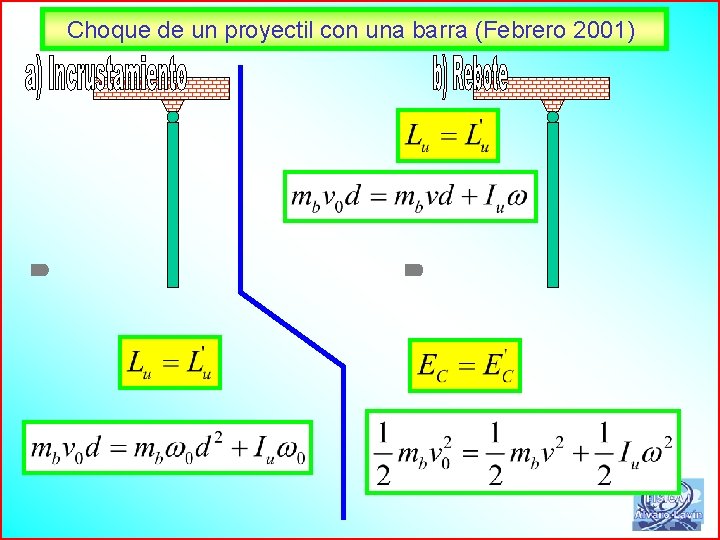
Choque de un proyectil con una barra (Febrero 2001) 70

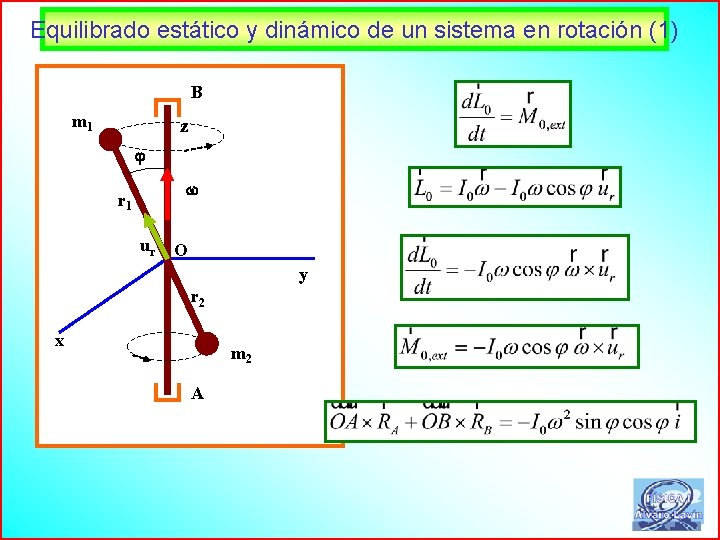
Equilibrado estático y dinámico de un sistema en rotación (1) B m 1 z r 1 ur O y r 2 x m 2 A 71

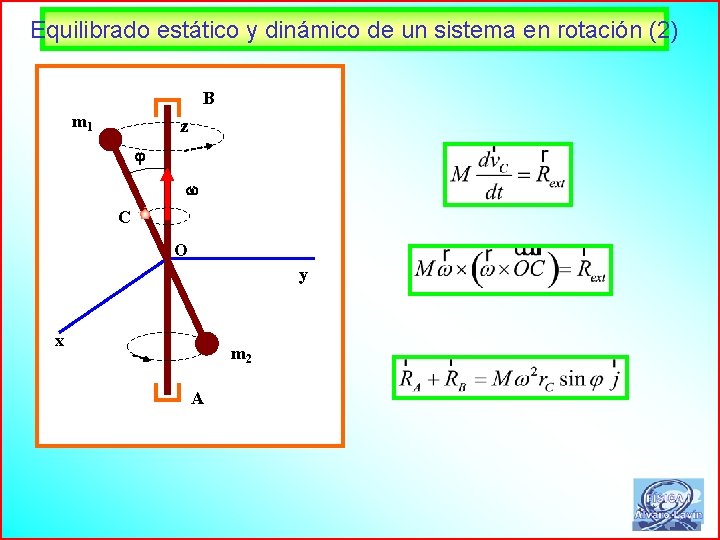
Equilibrado estático y dinámico de un sistema en rotación (2) B m 1 z C O y x m 2 A 72

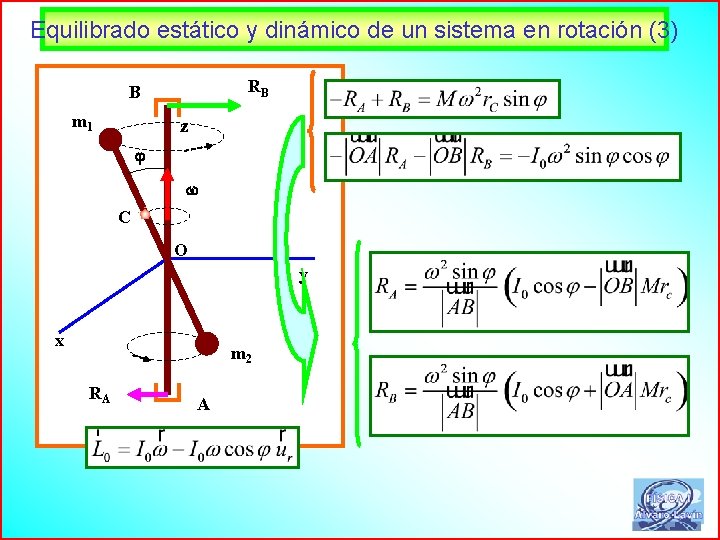
Equilibrado estático y dinámico de un sistema en rotación (3) RB B m 1 z C O y x m 2 RA A 73

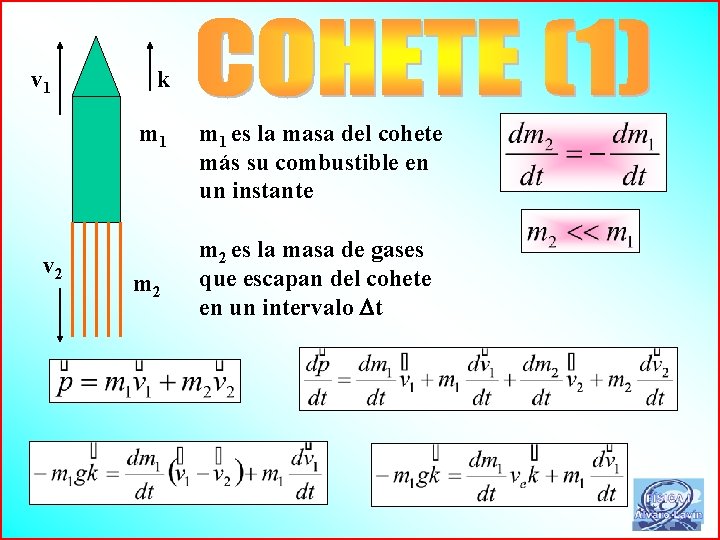
v 1 k m 1 v 2 m 1 es la masa del cohete más su combustible en un instante m 2 es la masa de gases que escapan del cohete en un intervalo t 74

v 1 k m 1 v 2 m 1 es la masa del cohete más su combustible en un instante m 2 es la masa de gases que escapan del cohete en un intervalo t 75

v 1 k m 1 v 2 m 2 76