Unit 8 Chemical Kinetics Thermodynamics Chemical Kinetics Chemical

Unit 8 Chemical Kinetics & Thermodynamics

Chemical Kinetics • Chemical kinetics is the study of the factors that affect the speed of a reaction and the mechanism by which a reaction proceeds. • Rate is how much a quantity changes in a given period of time.

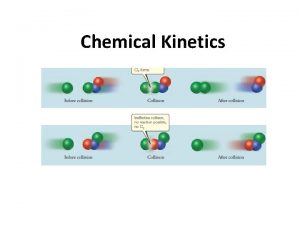
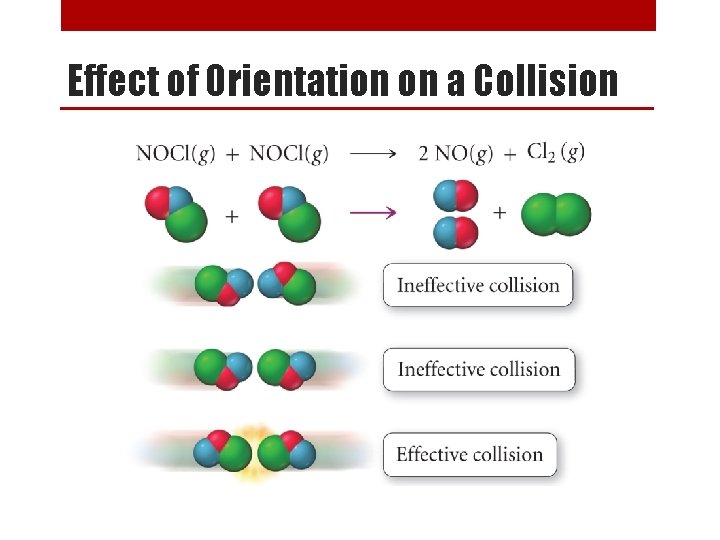
Collision Theory • Collision Theory says that in order for reactions to occur between substances, particles must collide. • For a collision to be effective, particles must: 1. Collide with sufficient energy. 2. Have a favorable orientation.

Effect of Orientation on a Collision

Rate-Influencing Factors • The rate of a chemical reaction depends on the number of collisions between particles. • Rate-influencing factors are: • Nature of Reactants • Surface Area Smaller pieces = larger surface area • Temperature • Concentration • Presence of Catalysts Visual Concept

Effect of Concentration • The rate of a reaction often depends on the concentration of one or more of the reactants. • Greater concentration of reactant particles = more collisions = increase in reaction rate.

Rate Law Expressions • Rate law equations are based on the Molarity concentrations of the reactant(s). (Indicate Molarity concentrations with brackets. ) • The Rate (R) involves the product of the concentrations of the individual reactants. • Experiments have proven that coefficients of reactants have an exponential effect on R. Ex: For the equation R = k [A][B]2 A+2 B→C (k = rate law constant)

Rate Law Expressions Sample Problem For the following single-step chemical reaction: 2 SO 2 + O 2 → 2 SO 3 1. Write the rate law expression. R = k [SO 2]2 [O 2] 2. What happens to the Rate if the [SO 2] is cut by ½? Rate is 4 x slower 3. What happens to the Rate if the [O 2] is tripled? Rate is 3 x greater

Reaction Mechanism • Chemical reactions often occur as a series of consecutive steps (this is called a reaction mechanism. ) • Products in an early step that are reactants in a later step are called intermediates. Example: Overall reaction: H 2(g) + 2 ICl(g) 2 HCl(g) + I 2(g) Mechanism: intermediate 1) H 2(g) + ICl(g) HCl(g) + HI(g) 2) HI(g) + ICl(g) HCl(g) + I 2(g)

Rate-Determining Step • One of the steps will always occur at a slower rate than the others. • The rate-determining step is the slowest step (bottleneck) in a reaction mechanism. • ONLY the rate-determining step is used for rate law expressions.

Rate-Determining Step Sample Problem Equation: 2 NO 2 + F 2 → 2 NO 2 F Step 1: NO 2 + F 2 → NO 2 F + F Step 2: F + NO 2 → NO 2 F Rate-determining step “slow” “fast” 1. Write the rate law expression for this reaction. R = k [NO 2] [F 2] 2. Given the following data, calculate the [NO 2] used: R = 0. 00905 M/s, k = 1. 44 x 10 -3 1/M s, [F 2] = 1. 11 M R 0. 00905 M/s [NO 2] = k [F ] = (1. 44 x 10 -3 1/ )(1. 11 M) 2 Ms ● ● [NO 2] = 5. 66 M

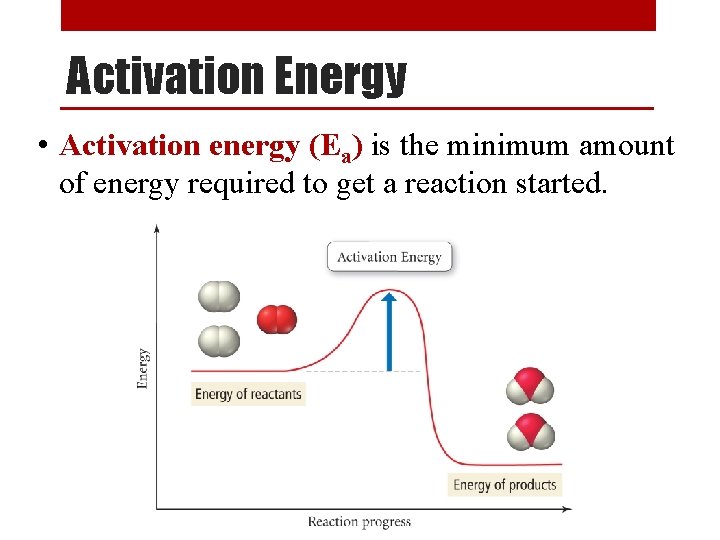
Getting a Reaction Started • Energy is needed to overcome the repulsion between molecules and get a reaction started. • Just as a ball cannot get over a hill without added energy, a reaction cannot occur unless the molecules have enough energy to get over this initial energy barrier.

Activation Energy • Activation energy (Ea) is the minimum amount of energy required to get a reaction started.

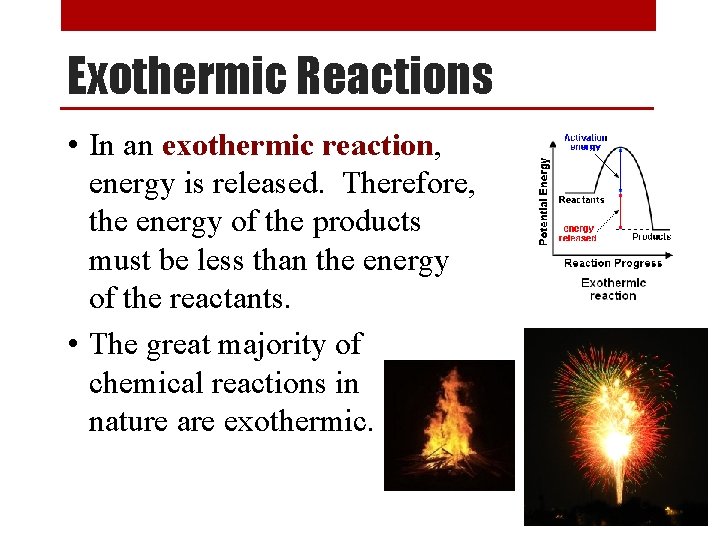
Exothermic Reactions • In an exothermic reaction, energy is released. Therefore, the energy of the products must be less than the energy of the reactants. • The great majority of chemical reactions in nature are exothermic.

Endothermic Reactions • In an endothermic reaction, energy is absorbed. Therefore, the energy of the products must be greater than the energy of the reactants.

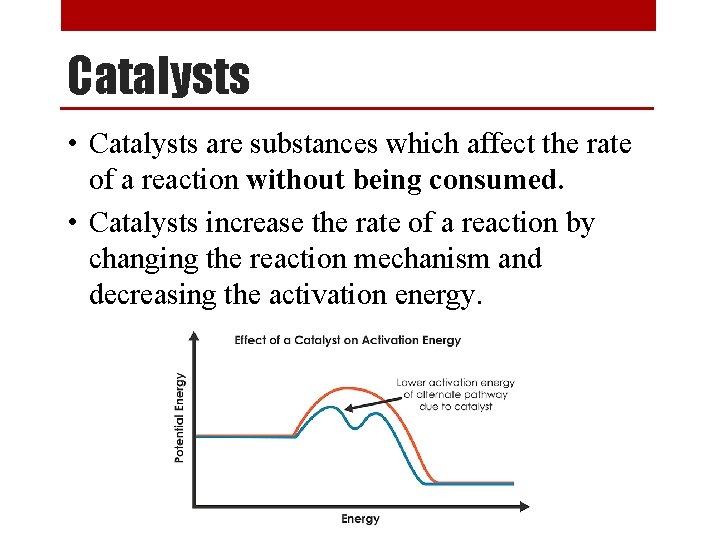
Catalysts • Catalysts are substances which affect the rate of a reaction without being consumed. • Catalysts increase the rate of a reaction by changing the reaction mechanism and decreasing the activation energy.

Enzymes • Due to the complexity of organic molecules, most biological reactions need a catalyst to proceed at a reasonable rate. • Protein molecules that catalyze biological reactions are called enzymes. • Enzymes pull the reactants onto an active site that orients them for the reaction.

Rate Order • Experiments have shown that there are 3 ways that a reactant’s concentration can affect the overall rate of the reaction: • Rate Order 0 ([X]0) - The concentration of a reactant has no effect on reaction rate. • Rate Order 1 ([X]1) - The concentration of a reactant has a direct effect on reaction rate. • Rate Order 2 ([X]2) - The concentration of a reactant has an exponential effect on reaction rate. • The order of a reaction can be determined only by experiment.

Determining the Order of a Reaction [A] (M) x 2 0. 10 Rate (M/s) [A] (M) Rate (M/s) 0. 015 x 2 0. 10 0. 015 x 1 x 2 0. 10 0. 015 x 4 0. 20 0. 030 0. 20 0. 015 0. 20 0. 060 0. 40 0. 015 0. 40 0. 240 When [A] doubles, the rate doubles When [A] doubles, rate doesn’t change When [A] doubles, the rate quadruples First Order Zero Order Second Order Rate = k[A]1 Rate = k[A]0 = k Rate = k[A]2

Rate Order of a Reaction Sample Problem x 2 [NO 2] (M) 0. 10 [CO] (M) Rate (M/s) 0. 10 constant 0. 0021 0. 20 0. 10 0. 20 constant 0. 20 0. 40 0. 10 x 4 0. 0082 x 2 0. 0083 x 1 0. 033 From the data above, determine the following: 1. Rate order of each reactant. second order in [NO 2] and zero order in [CO] 2. Overall rate order of the reaction. 2+0=2 second order reaction 3. The rate law for the reaction. Rate = k [NO 2]2

Finding the Rate Constant Sample Problem [NO 2] (M) [CO] (M) Rate (M/s) 0. 10 0. 0021 0. 20 0. 10 0. 0082 0. 20 0. 0083 0. 40 0. 10 0. 033 Use data from any one line of chart to find k Using the data above, and the rate law we just found, (R = k [NO 2]2), determine the following: 0. 0021 M/s 1. Value of k. k = R -1 s-1 = = 0. 21 M [NO 2]2 (0. 10 M)2 2. Reaction rate when the concentration of [NO 2] is 0. 50 M and [CO] is 1. 00 M. R = k [NO 2]2 = (0. 21 M-1 s-1) (0. 50 M)2 = 0. 053 M/s

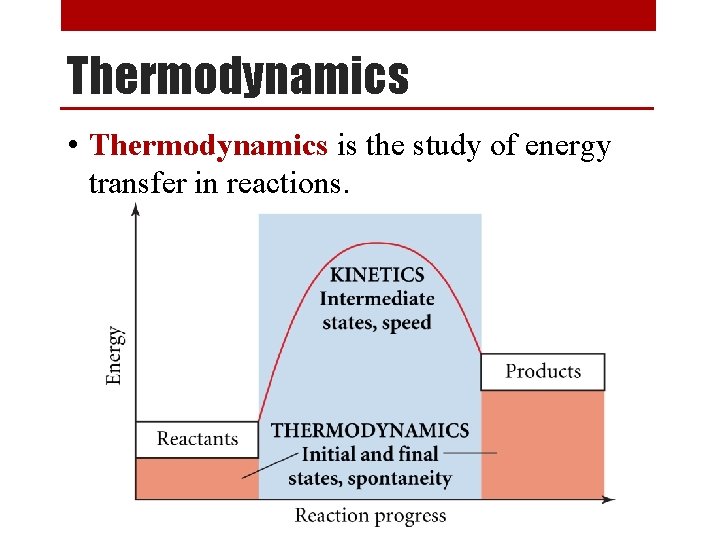
Thermodynamics • Thermodynamics is the study of energy transfer in reactions.

Energy • Energy is the ability to do work. • Some forms of energy are: • • • Mechanical (kinetic and potential) Electrical Heat or thermal Light or radiant Nuclear Chemical • Energy is commonly measured in joules. • 1 joule is the amount of energy needed to move a 1 kg mass at a speed of 1 m/s. (1 J = 1 )

First Law of Thermodynamics • The First Law of Thermodynamics is the Law of Conservation of Energy which states that energy cannot be created or destroyed. • However, energy can be transferred between objects, or between forms. (Ex: heat → light → sound)

Energy Exchange • Conservation of Energy requires that the total energy change in a system and its surroundings must be zero. • Energy is exchanged between system and surroundings through either heat exchange or work being done. • Heat is the exchange of thermal energy between a system and its surroundings.

Enthalpy • the Enthalpy change (DH) of a reaction is the heat exchanged in a reaction under conditions of constant pressure. • DH for a reaction is equal to the difference between the DH of formation of the products and the reactants. DHrxn = S n. DHf(products) - S n. DHf(reactants) • S means sum • n is the coefficient • Elements in their standard state have a DHf of zero.

Calculating Enthalpy of Reaction Sample Problem Calculate the Enthalpy Change in the Reaction: 2 C 2 H 2(g) + 5 O 2(g) 4 CO 2(g) + 2 H 2 O(l) Reactant/ DHf Product (k. J/mol) C 2 H 2(g) +227. 4 CO 2(g) -393. 5 H 2 O(l) -285. 8 DHrxn = S n. DHf(products) - S n. DHf(reactants) DHrxn = [(4 • DHCO 2 + 2 • DHH 2 O) – (2 • DHC 2 H 2 + 5 • DHO 2)] DHrxn = [(4 • (-393. 5) + 2 • (-285. 8)) – (2 • (+227. 4) + 5 • (0))] DHrxn = -2145. 6 k. J – 454. 8 k. J DHrxn = -2600. k. J

Stoichiometry Involving ∆H • The amount of heat generated or absorbed during a reaction depends on the amount of the substances reacting. Example: C 3 H 3(g) + 5 O 2(g) → 3 CO 2(g) + 4 H 2 O(g) ∆H = -2044 k. J Means 2044 k. J of heat is given off when 1 mole of C 3 H 3 reacts, or when 3 moles of CO 2 is produced. • These relationships can be used as ratios in stoichiometric conversions.

Stoichiometry Involving ∆H Sample Problem Ammonia reacts with oxygen as follows: 4 NH 3(g) + 5 O 2(g)→ 4 NO(g) + 6 H 2 O(g) ∆H = -906 k. J Calculate the heat (in k. J) associated with the complete reaction of 155 g of NH 3. 155 g NH 3 1 mol NH 3 -906 k. J 17. 0 g NH 3 4 mol NH 3 = -2070 k. J NH 3

Hess’s Law • Hess’s Law – the overall enthalpy change in a reaction is equal to the sum of enthalpy changes for the individual steps in the process. • Possible steps in Hess’s Law: 1. Reverse equation/ change sign on ΔH. 2. Multiply or Divide coefficients/multiply or divide ΔH.

Hess’s Law Sample Problem Calculate the enthalpy of formation for CH 4: C(s) + 2 H 2(g) → CH 4(g) ∆Hf = ? -74. 3 k. J The component reactions are: C(s) + O 2(g) → CO 2(g) ∆Hc = -393. 5 k. J 2 H 2(g) + ½O 2(g) → 2 H 2 O(l) -571. 6 k. J ∆Hc = -285. 8 CH 4(g) + 2 O 2(g) → CO 2(g) + 2 H 2 O(l) ∆Hc = -890. 8 k. J CO 2(g) + 2 H 2 O(l) → CH 4(g) + 2 O 2(g) ∆Hc = +890. 8 k. J - 2 moles of H 2 are used to make CH 4, -74. 3 k. J so multiply the 2 nd equation by 2 (including ∆H. ) - CH 4 is on the products side, not the reactants side, so reverse the 3 rd reaction and change the sign on ∆H. - Cancel unwanted terms and add the ∆H’s.

Sign of ∆H • In an exothermic reaction, the energy of the products is less than the energy of the reactants, so ∆H is negative. • In an endothermic reaction, the energy of the products is greater than the energy of the reactants, so ∆H is positive. Exothermic ∆H < 0 Endothermic ∆H > 0

Spontaneous Processes • A spontaneous process is one that occurs without ongoing outside intervention. • A nonspontaneous process is not impossible, but it requires energy input. • if a process is spontaneous in one direction, it must be nonspontaneous in the other.

Enthalpy and Reaction Tendency • Most spontaneous reactions are exothermic (∆H is negative). • Products have less energy than reactants. • Less energy = greater stability. • But not all spontaneous reactions are exothermic. • Ex: The melting of ice is endothermic and spontaneous (at >0 o. C). • Enthalpy must not be the sole criteria for spontaneity.

Entropy • Entropy (S) is a measure of the degree of disorder in a system. • Changes that increase entropy: • Physical state (phase) changes (solid < liquid < gas) • A larger number of moles of products than reactants • Increase in temperature • Solids dissociating into ions upon dissolving • Expansion (greater volume) of gases

Second Law of Thermodynamics • The Second Law of Thermodynamics states that for any spontaneous process, the entropy of the universe increases (DSuniv is positive). • The entropy of the system could decrease as long as the entropy of the surroundings increases by a greater amount. (DSuniv = DSsys + DSsurr)

Temperature Dependence of DS • The increase in DSsurr often comes from the heat released in an exothermic reaction. • the amount the entropy of the surroundings changes depends on the temperature it is at originally. • the higher the original temperature, the less effect addition or removal of heat has.

Gibbs Free Energy • The total amount of energy available in the system to do work on the surroundings is called the Gibbs Free Energy (DG). • DG can be calculated using the following equation (T is the Kelvin temperature): DG = DH – TDS • Systems tend toward lower Gibbs free energy (lower chemical potential. ) • A negative DG = a spontaneous reaction. • A positive DG = a nonspontaneous reaction.

Gibbs Free Energy Sample Problem Given: CCl 4(g) C(s, graphite) + 2 Cl 2(g) DH = +95. 7 k. J and DS = +142. 2 J/K at 25°C. 1. Calculate DG and determine if it is spontaneous: DG = DH – TDS DG = 95. 7 x 103 J – (298 K) (142. 2 J/K) DG = +5. 33 x 104 J Nonspontaneous 2. Determine at what temperature (if any) the reaction becomes spontaneous: DG = DH – TDS < 0 Spontaneous at: 3 95. 7 x 10 J – T (142. 2 J/K) < 0 T > 673 K 95. 7 x 103 J < T (142. 2 J/K)

Effect on Spontaneity • When DH and DS have opposite signs, spontaneity does not depend on the temperature, but when they have the same sign it does. DG = DH – TDS

Third Law of Thermodynamics • The Third Law of Thermodynamics states that for a perfect crystal at absolute zero, absolute entropy (S) = 0. • So every substance that is not a perfect crystal at absolute zero has some energy from entropy. • Perfect crystals never occur in practice; imperfections just get "frozen in" at low temperatures. • Scientists have achieved temperatures extremely close to absolute zero.