Chemical Kinetics Chapter 12 Chemical Kinetics Chemical kinetics

Chemical Kinetics Chapter 12

Chemical Kinetics • Chemical kinetics: the study of the speed or rate of a reaction under various conditions • One of the main goals is to understand the steps by which a reaction takes place • Reaction mechanism: the series of steps by which a reaction takes place • We will explore rate laws, reaction mechanisms, and simple models for chemical reactions

Factors that Affect Reaction Rates • • • Nature of the reactants Concentration of reactants Temperature Presence of catalysts Surface area of reactants

Nature of the Reactants • Some molecules react in a hurry, others react very slowly • Physical state has a lot to do with this; some react better aqueous, some better as solids • Chemical identity is also a factor • Usually ions of opposite charge react very quickly • Usually the more bonds between reacting atoms in a molecule, the slower the reaction rate • Substances with strong bonds will react slowly

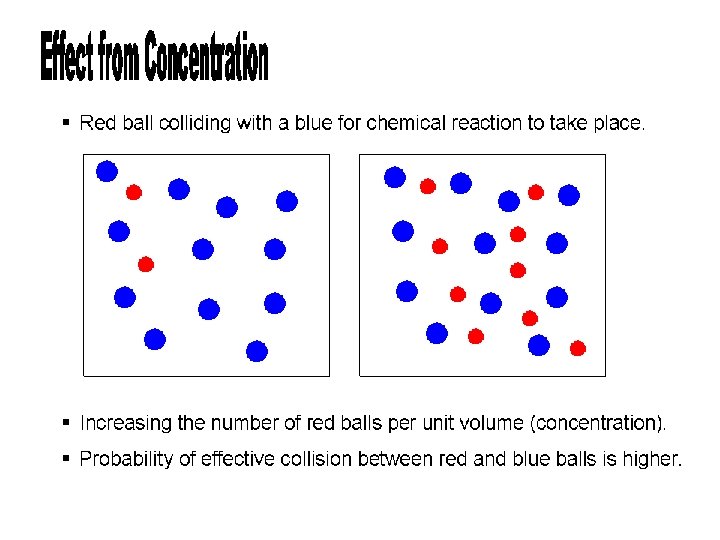
Concentration of the Reactants • If there are molecules present, then more collisions will occur • As we will study later, more collisions relates to a higher reaction rate • If you increase the pressure of a gas, the volume decreases, and this results in an increase in concentration

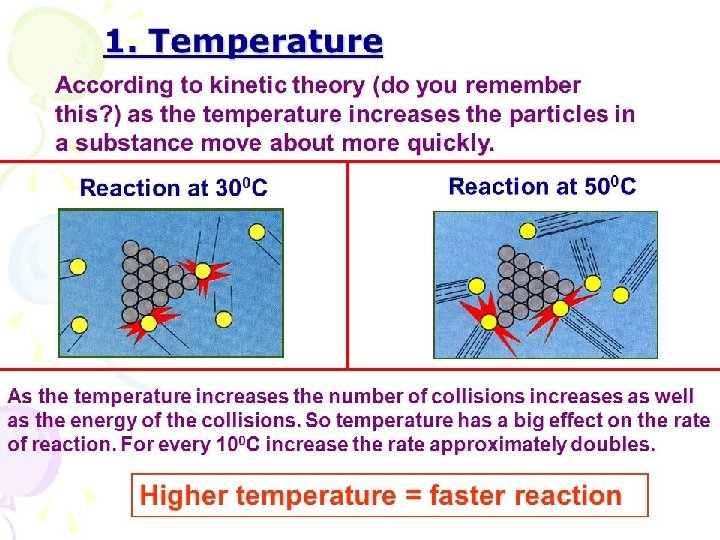
Temperature • “heat ‘em up, speed ‘em up” • The faster they move, the more likely they are to collide • An increase in temperature produces more successful collisions that are able to overcome the needed activation energy • Generally, an increase in temperature causes an increase in reaction rate

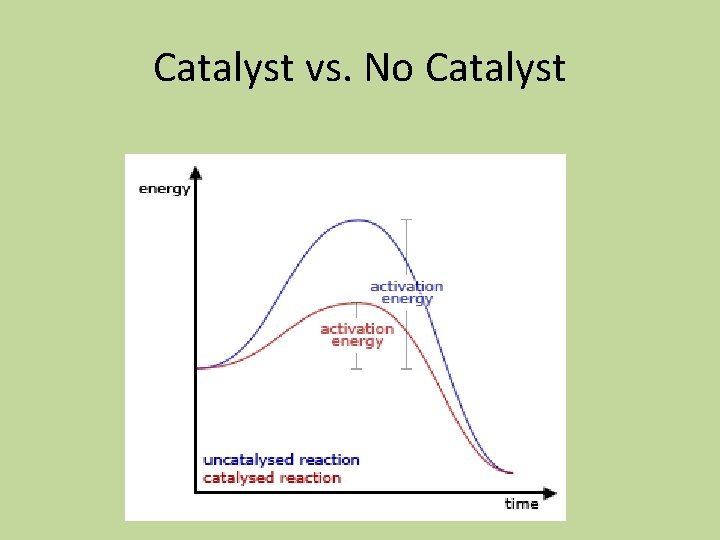
Catalyst • A catalyst is a substance that changes the rate of a reaction by altering the reaction pathway • Most work by lowering the activation energy needed by providing a new mechanism or pathway for the reaction • The catalyst is not part of the chemical reaction and is not used up during the reaction • Biological catalysts are proteins called enzymes

Surface Area of the Reactants • Except for substances in the gaseous state or in solution, reactions occur at the boundary, or interface, between two phases • The greater surface area exposed, the greater chance of collisions between particles, so the reaction will proceed at a much faster rate • Smaller pieces means greater surface area

The large chunk of blue molecules can only react with the red molecules around the edges The smaller pieces of blue molecules can react with the red molecules around much more area

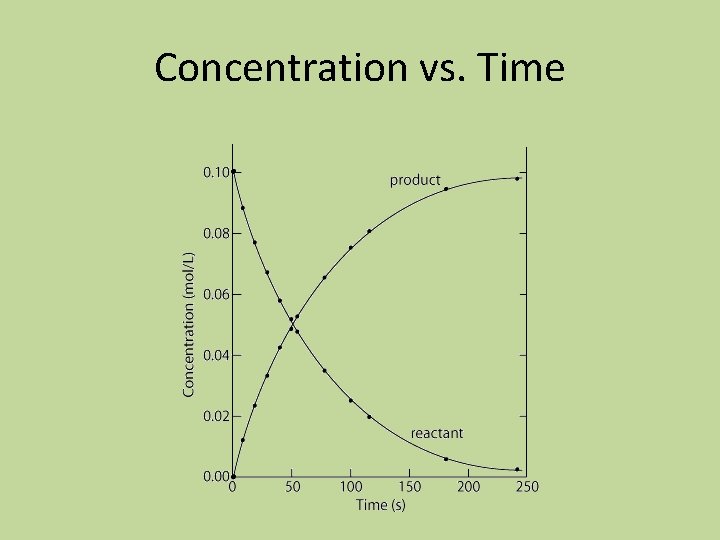
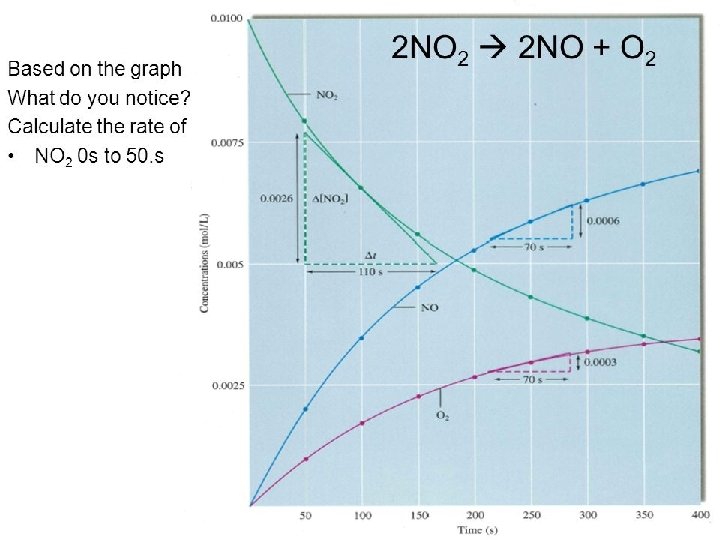
12. 1 Reaction Rates • The rate of a process is defined as the change in a given quantity over a specific period of time • Reaction rate of a chemical reaction: the change in concentration of a reactant or product per unit of time • rate = change in concentration of A = Δ[A] t 2 – t 1 Δt

Concentration vs. Time

Rate of Reactants • The concentrations of reactants always (initially) decrease with time, so any rate expression involving a reactant will include a negative sign • It is customary to work with positive reaction rates, so the rate of a reaction with respect to a reactant is found by: − Δ[A] Δt

Instantaneous Rate • Instantaneous rate: the value of the rate at a particular time • Can be obtained by computing the slope of a line tangent to the curve at that point

Answer • NO 2 from 0 s to 50. s • It is hard to see the value at 50. s from the graph, so it is given as 0. 0079 mol/L • The Δ is always (final – initial) • − (0. 0079 mol/L – 0. 0100 mol/L) = 50. s – 0 s • 4. 2 x 10 -5 mol/L s

Relative Rates from the Balanced Equation • You must consider that the reactants’ concentrations are decreasing as the products’ concentrations are increasing • 4 PH 3(g) P 4(g) + 6 H 2(g) • Initial reaction rate: • − ¼ [ΔPH 3/Δt] = + [ΔP 4/Δt] = +⅙ [ΔH 2/Δt] • Can multiply each by 12 and get 3 times the rate of PH 3 disappearance is relative to 12 times the rate of P 4 appearance and 2 times the rate of H 2 appearance

Example • What are the relative rates of change in concentration of the products and reactant in the decomposition of nitrosyl chloride, NOCl? • 2 NOCl(g) 2 NO(g) + Cl 2(g)

12. 2 Rate Laws: An Introduction • Rate law: an expression that shows how the rate of reaction depends on the concentration of reactants • Rate constant (k): the proportionality constant in the relationship between reaction rate and reactant concentrations • Order (of reactant) (n): the positive or negative exponent, determined by experiment, of the reactant concentration in a rate law

Two Important Facts • The concentrations of the products do not appear in the rate law because the reaction rate is being studied under conditions where the reverse reaction does not contribute to the overall rate • The value of the exponent n must be determined by experiment; it cannot be written from the balanced equation

Example Rate Law • Consider: 2 NO 2(g) 2 NO(g) + O 2(g) • The rate law would be: rate = k[NO 2]n • n will be determined experimentally

Two Types of Rate Laws • Differential rate law (AKA rate law): shows how the rate of a reaction depends on concentrations • Integrated rate law: shows how concentrations of species in the reaction depend on time • We can use either one to infer the steps by which the reaction occurs (main purpose of a rate law)

12. 3 Determining the Form of the Rate Law • To find the exact relation between rate and concentration, we must conduct experiments and collect information • a. A + b. B x. X • Initial reaction rate = k[A]m[B]n • [A] and [B] are the concentrations of each reactant • m = order of reaction for reactant A • n = order of reaction for reactant B

Order of a Reaction • The overall order of the reaction is the sum of the powers, as in m + n +… • The order can only be determined experimentally (not from stoichiometry)

Determine the Order of a Reaction • If you double the concentration of one species, like A, while the other conditions are held constant, and there is no effect on the initial rate of reaction, then the reaction is zero order with respect to A (as in 20 = 1) (these are not very common) • If it doubles the rate, then the reaction is first order with respect to A (as in 21 = 2) (these are very common)

More on Order Determination • If doubling the concentration of A, while the other conditions are held constant causes an increase of the rate by a factor of four, it is second order with respect to A (as in 22 = 4) • Common, especially in gas-phase reactions

Using “Table Logic” • When viewing a table of data considering initial rates and initial concentrations: • Look for two trials where the concentration of a reactant was held constant • Next, focus on the other reactant. Ask yourself how its concentration changed for the same two trials. Was it doubled, tripled, halved, etc. ?

Table Logic • Once you have determined the factor by which the concentration of the other reactant was changed, determine how that affected the rate for those same two trials. • If changing the concentration had zero effect on the rate, then that reactant is to zero order and the reaction does not depend on the concentration of that reactant at all (it will not show up in the rate law expression)

Table Logic • Examine the data table again. This time look for trials where the concentration of the reactant you just determined the order for is held constant, and repeat for any other reactants. • You will want to record which experiments you compared for each reactant

Example Table Experiment number Initial rate in mol/L s Initial concentration [A]0 Initial concentration [B]0 1 0. 50 x 10 -2 0. 50 0. 20 2 0. 50 x 10 -2 0. 75 0. 20 3 0. 50 x 10 -2 1. 00 0. 20 4 1. 00 x 10 -2 0. 50 0. 40 5 1. 50 x 10 -2 0. 50 0. 40

What is the order of the reaction with respect to each reactant and overall? • Consider experiments 1 and 2. The [B]0 does not change, the [A]0 does change, but the rate does not change. The reaction is zero order with respect to A. • Consider experiments 1 and 5. The [A]0 does not change, the [B]0 triples, and the rate triples. The reaction is first order with respect to B • Rate = k[B] overall order is 1

To Calculate the Rate Constant • The rate constant is only affected by changes in temperature and particle size (if a solid is involved) • It is unaffected by changes in the concentrations of the reactants • For the previous series of experiments, you can choose any results, but I usually use the first one because it is handy. • k = rate/[B] = (0. 50 x 10 -2 mol/L s)÷ 0. 20 mol/L • k = 0. 025 s-1

Calculate the order of each reactant, the overall order, and calculate k. Experiment [A] mol/L [B] mol/L [C] mol/L Initial rate mol/L s 1 0. 400 1. 600 0. 0600 4. 86 x 10 -3 2 0. 800 1. 600 0. 0600 9. 72 x 10 -3 3 0. 400 0. 800 0. 0600 4. 86 x 10 -3 4 0. 800 1. 600 0. 1800 87. 5 x 10 -3

Work Here

Work Here

Example 12. 1 on page 562 • Read the example in the book and notice the “ugly algebra” method • You can usually still use table logic which is faster and just as efficient.

One More • In the following reaction, a Co-Cl bond is replaced by a Co-OH 2 bond. Using the data below, find the value of m in the rate expression and calculate the value of k. • [Co(NH 3)5 Cl]+2 + H 2 O [Co(NH 3)5 H 2 O]+3 + Cl Experiment [[Co(NH 3)5 Cl]+2] mol/L Initial rate mol/L min 1 2 3 4 1. 0 x 10 -3 2. 0 x 10 -3 3. 0 x 10 -3 1. 3 x 10 -7 2. 6 x 10 -7 3. 9 x 10 -7 1. 3 x 10 -7

Initial rate = k[[Co(NH 3)5 Cl]+2]m • Work Here

12. 4 Integrated Rate Law • The integrated rate law expresses the concentration of the reactant as a function of time • The data table contains concentration and time data • You will use graphical methods to determine the order of a given reactant

Value of k • The value of the rate constant k is equal to the absolute value of the slope of the best fit line • The best fit line is determined by performing 3 linear regressions and analyzing the regression correlation coefficient. (looking for the r value closest to 1) • The AP test will not make you perform this, but they will give you graphs that you then have to analyze

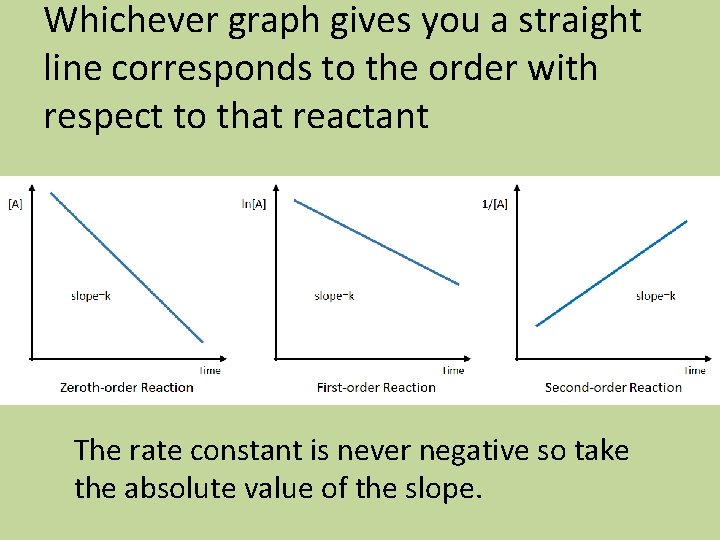
Whichever graph gives you a straight line corresponds to the order with respect to that reactant The rate constant is never negative so take the absolute value of the slope.

The Integrated First-order Rate Law • If [A]t is the concentration of A at any time, and [A 0] is the initial concentration, and the reaction is first-order with respect to [A], then: (this is on the cheat sheet) • ln[A]t – ln[A]0 = -kt

Data Table for the Graph ln[N 2 O 5] -2. 303 -2. 649 -2. 996 -3. 689 -4. 382 -5. 075 Time (s) 0 50 100 200 300 400

Verification of first-order by plotting ln[N 2 O 5] vs. time

Calculation of “k” • • • -slope = k -slope = (Δy/Δx) -slope = (-5. 075 − (-2. 303)) / (400 – 0) -slope = -6. 93 x 10 -3 s-1 slope = 6. 93 x 10 -3 s-1 k = 6. 93 x 10 -3 s-1

More Good Stuff • • What is the rate law for the previous reaction? Rate = 6. 93 x 10 -3 s-1[N 2 O 5] Calculate the rate at 600. s ln[N 2 O 5]t – ln[N 2 O 5]0 = -kt ln[N 2 O 5]t – ln(0. 1000) = - 6. 93 x 10 -3 s-1 (600. s) ln[N 2 O 5]t – (-2. 303) = -4. 158 ln[N 2 O 5]t = -6. 461 [N 2 O 5]t = 0. 0015632 = 0. 00156 M

Half-Life of a First-Order Reaction • Half-life of a reactant (t½): the time required for a reactant to reach half its original concentration • Here is the general equation for the half-life of a first-order reaction (on the cheat sheet): • t½ = 0. 693/k • Half-life does not depend on concentration • To solve for the decimal that remains: (½)#half-lives

Example • A certain first-order reaction has a half-life of 20. 0 minutes. Calculate the rate constant for this reaction. • t½ = 0. 693/k • So k = 0. 693/t½ • k = 0. 693/20. 0 • k = 0. 0347 min-1

Second-Order Rate Laws • For a general reaction involving a single reactant, that is, • a. A products • That is second order in A, the rate law is: • Rate = k[A]2 • The integrated second-order rate law has the form (on the cheat sheet): • 1 – 1 = kt [A]0

Second-Order Rate Laws • A plot of 1/[A] vs. time will produce a straight line with a slope equal to k.

Integrated Rate Laws for Reactions with More Than One Reactant • Must still be determined by experiment • A technique called “swamping” is used • You flood the reaction vessel with high concentrations of all but one reactant and perform the experiment • The reactants at high concentrations stay the same when compared to the reactant with a low concentration

This is used for the crystal violet lab (which we will do) • The rate is now dependent on the reactant with the low concentration since the other reactants aren’t changing much • Therefore the rate = k’ • This is called a pseudo-rate-law and k’ is a pseudo-rate-constant • Pseudo-rate-law: a law obtained by simplifying a more complicated one by swamping

Review Summary • There is an excellent summary of rate laws on pages 573 -574 in your textbook

12. 5 Reaction Mechanisms • Reaction mechanism: the series of elementary steps involved in a chemical reaction • One of the main purposes for studying kinetics is to learn as much as possible about the steps involved in a reaction • Consider: • NO 2(g) + CO(g) NO(g) + CO 2(g) • The rate law (from experiments) is found to be rate = k[NO 2]2

Reaction Mechanisms • This reaction is much more complicated than it seems. It is thought to involve two steps. • NO 2(g) + NO 2(g) NO 3(g) + NO(g) (k 1) • NO 3(g) + CO(g) NO 2(g) + CO 2(g) (k 2) • In this mechanism, NO 3 is an intermediate • Intermediate: a species that is neither a reactant nor a product but that is formed and consumed in the reaction sequence

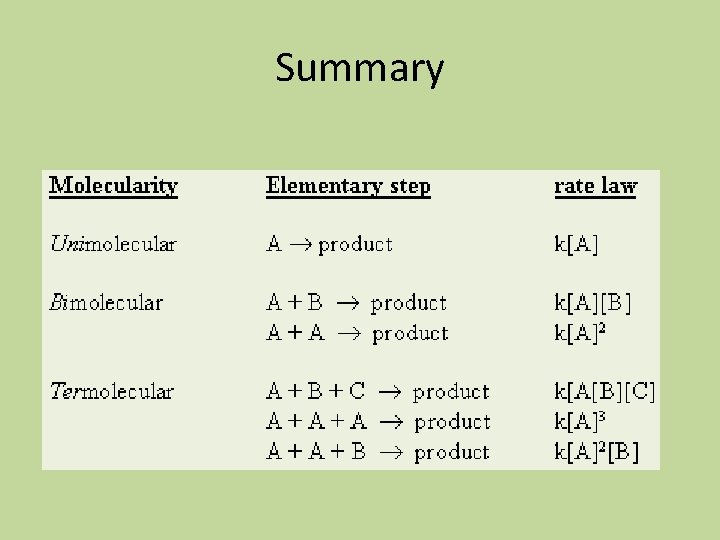
Elementary Step and Molecularity • Each of the two reactions is called an elementary step • Elementary step: a reaction whose rate law can be written from its molecularity • Molecularity: the number of species that must collide to produce the reaction indicated by that step

Molecularity • Unimolecular: a reaction involving one molecule • Bimolecular: a reaction involving the collision of two molecules • Termolecular: a reaction involving the simultaneous collision of three molecules (rare)

Summary

Reaction Mechanism Defined • A series of elementary steps that must satisfy two requirements: 1. The sum of the elementary steps must give the overall balanced equation for the reaction 2. The mechanism must agree with the experimentally determined rate law

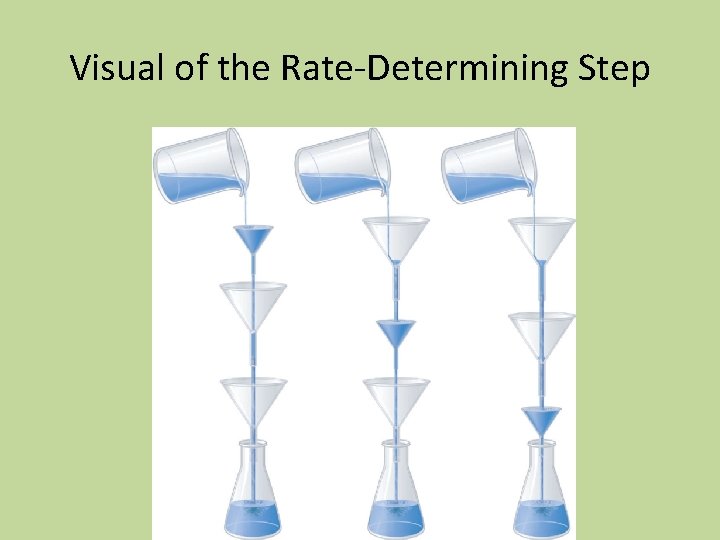
Rate-Determining Step • Rate-determining step: the slowest step in a reaction mechanism, the one determining the overall rate • The overall reaction can be no faster than the slowest step in the sequence • Deducing a mechanism is sometimes quite difficult • The rate law is always determined first, and then the previous 2 rules are followed to propose a mechanism that may or may not be correct

Visual of the Rate-Determining Step

Check for Mechanisms • • • Reaction I A + B X + C (slow) A+X D (fast) Overall reaction: 2 A + B C + D Rate = k[A][B] (because of the slow step)

Check For Mechanisms • • • Reaction II A + B X (fast) A + X C + D (slow) Overall reaction: 2 A + B C + D Rate = k[A]2[B] (because X depends on both A and B)

Check For Mechanisms • • Reaction III B X (slow) X + A Y + C (fast) Y + A D (fast) Overall reaction: 2 A + B C + D Rate = k[B] (because of the slow step)

Example • The gas-phase decomposition of N 2 O is believed to occur via two elementary steps: • N 2 O N 2 + O • N 2 O + O N 2 + O 2 • Experimentally the rate law is found to be rate = k[N 2 O] • Write the equation for the overall reaction • Identify any intermediates • Determine the rate-determining step

Answers Here

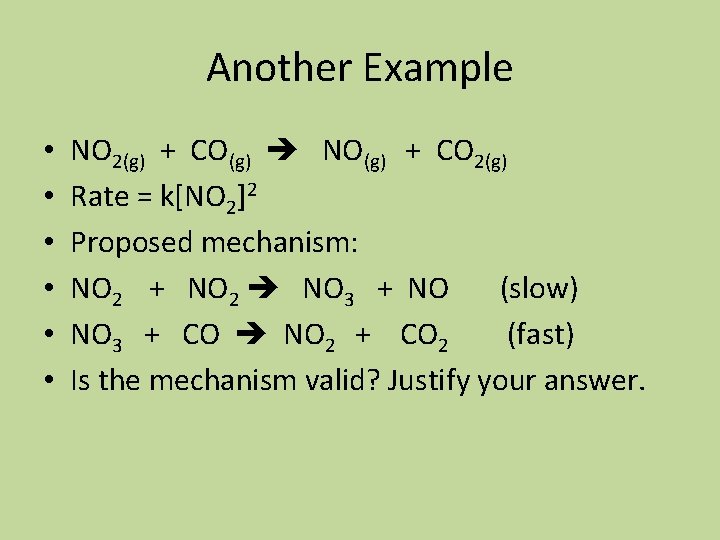
Another Example • • • NO 2(g) + CO(g) NO(g) + CO 2(g) Rate = k[NO 2]2 Proposed mechanism: NO 2 + NO 2 NO 3 + NO (slow) NO 3 + CO NO 2 + CO 2 (fast) Is the mechanism valid? Justify your answer.

Answer Here

Another Example 2 NO(g) + O 2(g) 2 NO 2(g) Proposed mechanism: NO(g) + O 2(g) NO 3(g) (fast) NO 3(g) + NO(g) 2 NO 2(g) (slow) Propose a rate law consistent with this mechanism • Does the mechanism meet the stoichiometry requirement? Justify your answer. • • •

Answers Here

12. 6 A Model for Chemical Kinetics • Chemical reactions speed up when the temperature is increased

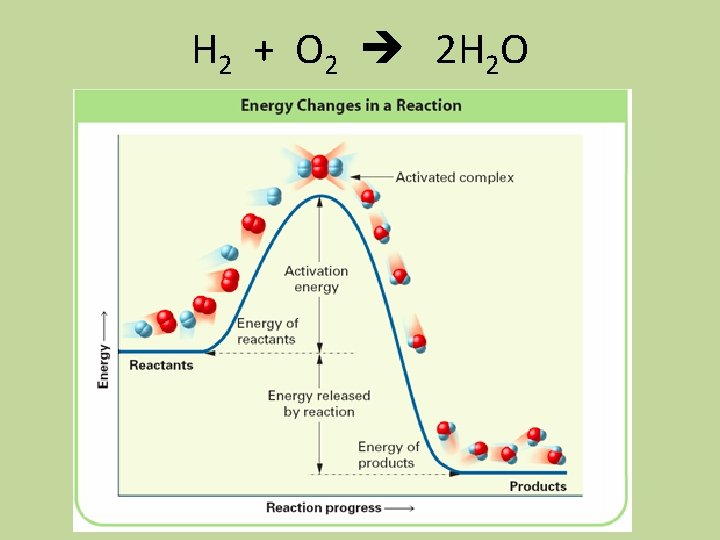
Collision Model • Collision model: a model based on the idea that molecules must collide to react • Activation energy: the threshold energy that must be overcome to produce a chemical reaction • Activated complex (transition state): the arrangement of atoms found at the top of the potential energy barrier as a reaction proceeds from reactants to products

H 2 + O 2 2 H 2 O

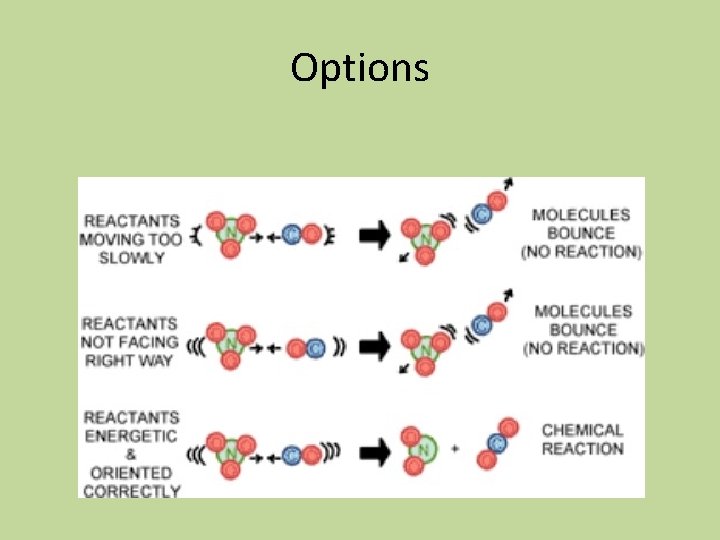
Colliding Particles • Only two particles may collide at a time • Proper orientation of colliding molecules is important so that the atoms can come in contact with each other to become products • The collision must occur with enough energy to overcome the e-/e- repulsion of the valence electrons and must have enough energy to transform translational energy into vibrational energy in order to penetrate into each other so that the electrons can rearrange and form new bonds

Options

Summary of Requirements for a Reaction to Occur • The collision must involve enough energy to produce the reaction; that is, the collision energy must equal or exceed the activation energy • The relative orientation of the reactants must allow formation of any new bonds necessary to produce products

12. 7 Catalysis • Catalyst: a substance that speeds up a reaction without being consumed itself • It works by providing a new pathway (mechanism) with a lower activation energy, by enabling the formation of a new transition state, or stabilizing the intermediate • Enzyme: biological catalyst • Two types of catalysts: homogeneous and heterogeneous

Catalyst vs. No Catalyst

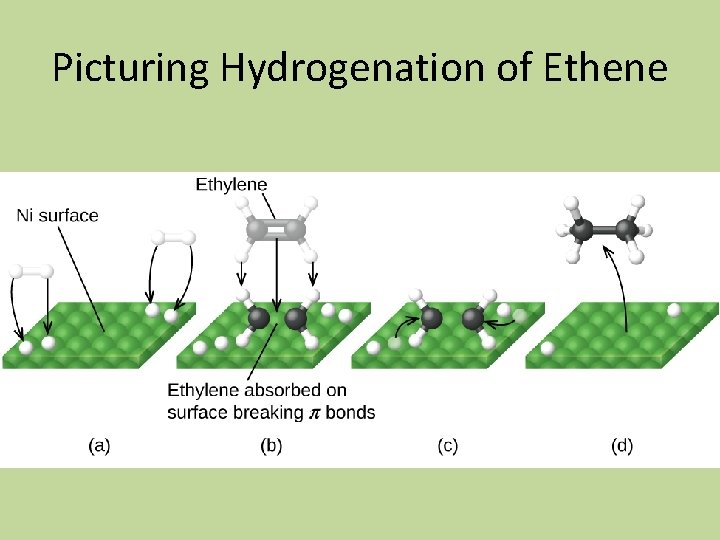
Heterogeneous Catalysis • Heterogeneous catalyst: exists in a different phase as the reacting molecules (usually as a solid) • This most often involves gaseous reactants being adsorbed on the surface of a solid catalyst • Adsorption: refers to the collection of one substance on the surface of another substance (not the same as absorption)

Adsorption vs. Absorption

Typical Heterogeneous Catalysis 1. adsorption and activation of the reactants 2. migration of the adsorbed reactants on the surface 3. reaction of the adsorbed substances 4. escape, or desorption, of the products

Picturing Hydrogenation of Ethene

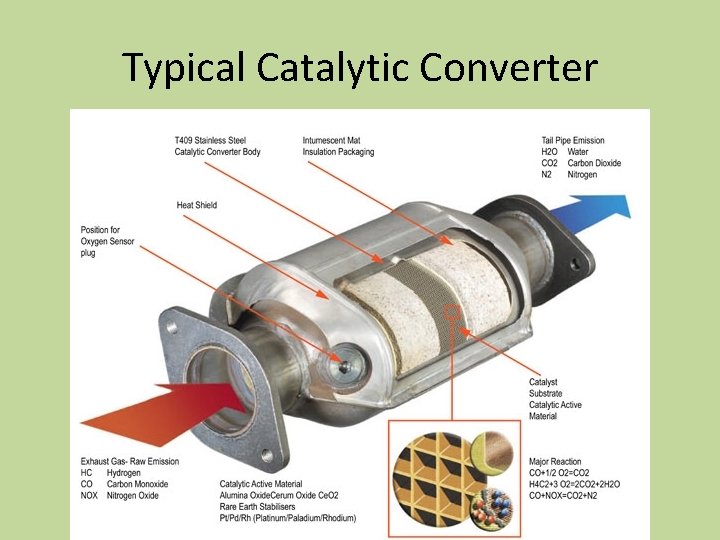
Catalytic Converter • Catalytic converters have been placed in automobiles since 1974 • A catalytic converter is an emissions control device that converts toxic gases and pollutants in exhaust gas to less toxic pollutants by catalyzing a redox reaction

How a Catalytic Converter Works

Typical Catalytic Converter

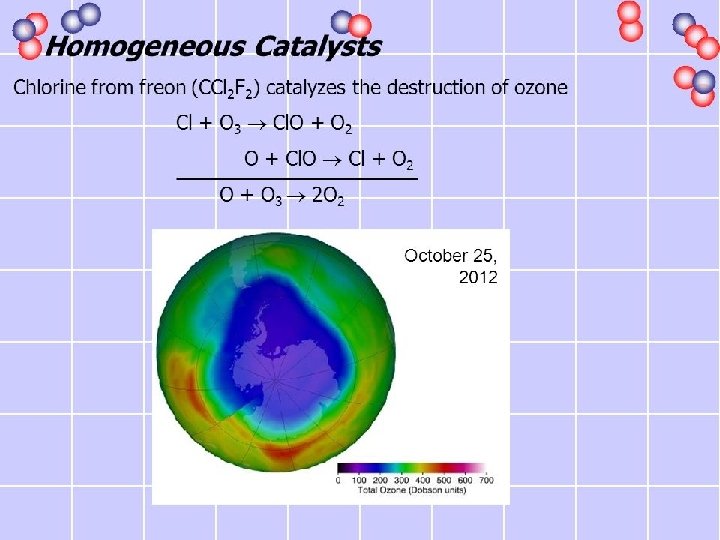
Homogeneous Catalysis • Homogeneous catalyst: one that exists in the same phase as the reacting molecules • One example is the production of ozone in the lower atmosphere by the reaction of NO with O 2 • NO is produced in any high-temperature combustion process where N 2 is present, such as the internal combustion engine in cars

More • A catalytic converter will convert some of the NO back to N 2, but significant amounts escape into the atmosphere to react: • 2 NO(g) + O 2(g) 2 NO 2(g) then the following occurs: • NO 2(g) NO(g) + O(g) and then: • O 2(g) + O(g) O 3(g) • NO is acting as a catalyst and is not consumed • Ozone is a powerful oxidizing agent that forms other substances irritating to the eyes and lungs, and is itself very toxic (powerful pollutant) light

In the Upper Atmosphere • In the upper atmosphere, nitric oxide is again catalytic, but here its effect is to change O 3 to O 2. • This is a potential problem because ozone, which absorbs ultraviolet light, is necessary to protect us from the harmful effects of this high-energy radiation • Freon, a formally used refrigerant, is decomposed in the upper atmosphere, forming Cl(g) molecules, which then catalyze the decomposition of O 3.