Biochemical Biophysical Kinetics Made Easy Software DYNAFIT in

Biochemical / Biophysical Kinetics “Made Easy” Software DYNAFIT in drug discovery research Petr Kuzmič, Ph. D. Bio. Kin, Ltd. 1. Theory: differential equation models - DYNAFIT software 2. Example: lantha. Screen® Eu assay in “kinetic” mode - p 38 a kinase / antibody / tracer / desatinib Bio/Chemical Kinetics Made Easy

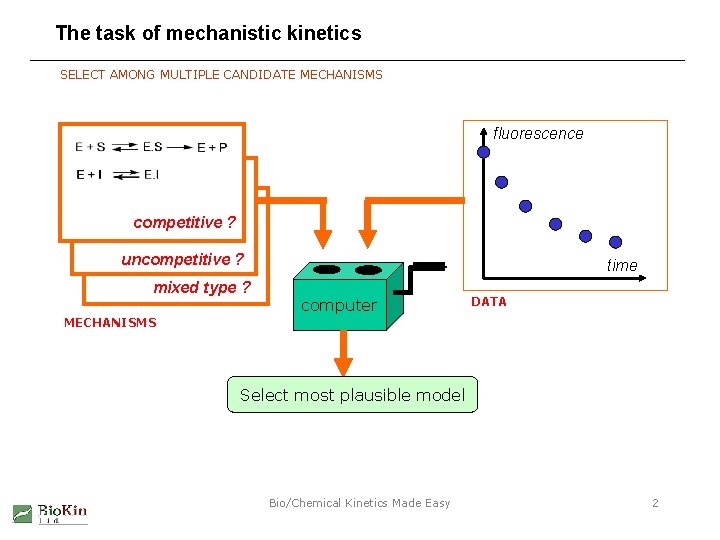
The task of mechanistic kinetics SELECT AMONG MULTIPLE CANDIDATE MECHANISMS fluorescence competitive ? uncompetitive ? mixed type ? time computer DATA MECHANISMS Select most plausible model Bio/Chemical Kinetics Made Easy 2

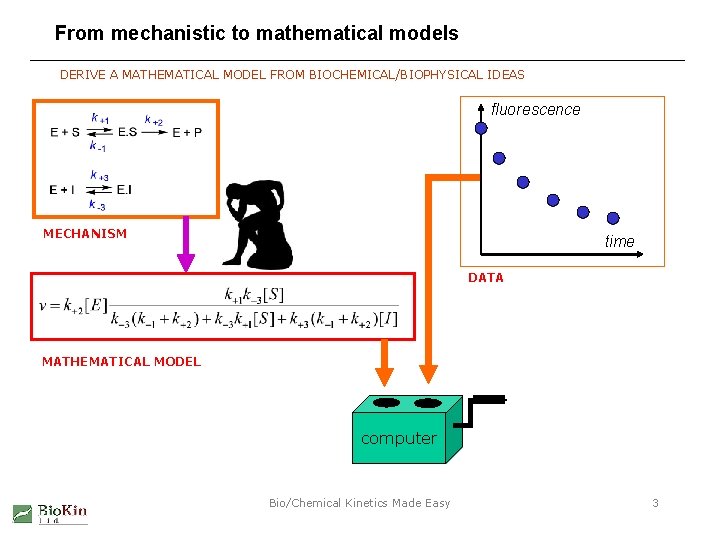
From mechanistic to mathematical models DERIVE A MATHEMATICAL MODEL FROM BIOCHEMICAL/BIOPHYSICAL IDEAS fluorescence MECHANISM time DATA MATHEMATICAL MODEL computer Bio/Chemical Kinetics Made Easy 3

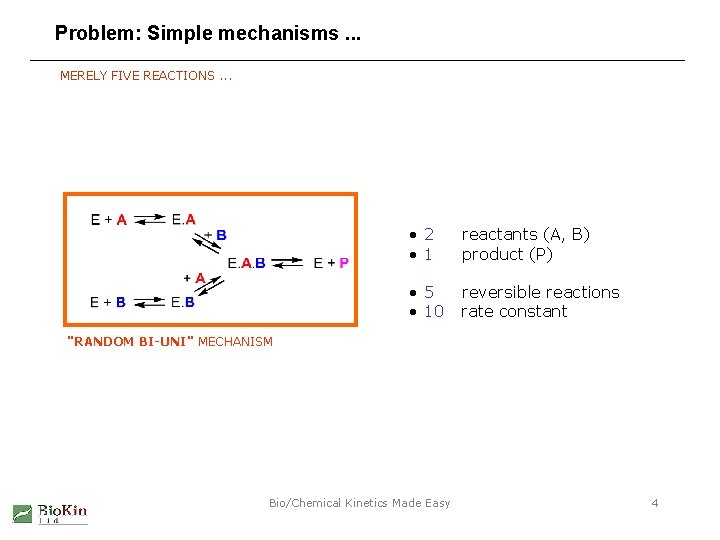
Problem: Simple mechanisms. . . MERELY FIVE REACTIONS. . . • 2 • 1 reactants (A, B) product (P) • 5 • 10 reversible reactions rate constant "RANDOM BI-UNI" MECHANISM Bio/Chemical Kinetics Made Easy 4

. . . lead to complex algebraic models MERELY FIVE REACTIONS. . . Segel, I. (1975) Enzyme Kinetics. John Wiley, New York, p. 646. "RANDOM BI-UNI" MECHANISM Bio/Chemical Kinetics Made Easy 5

New approach: Numerical Kinetics NO MORE ALGEBRA: LET THE COMPUTER DEAL WITH IT ! Bio/Chemical Kinetics Made Easy 6

Theoretical foundations: Mass Action Law RATE IS PROPORTIONAL TO CONCENTRATION(S) MONOMOLECULAR REACTIONS rate is proportional to [A] - d [A] / d t = k [A] BIMOLECULAR REACTIONS rate is proportional to [A] [B] - d [A] / d t = - d [B] / d t = k [A] [B] Bio/Chemical Kinetics Made Easy 7

Theoretical foundations: Mass Conservation Law PRODUCTS ARE FORMED WITH THE SAME RATE AS REACTANTS DISAPPEAR EXAMPLE - d[ A]/dt = + d[ P]/dt = + d[ Q]/dt COMPOSITION RULE ADDITIVITY OF TERMS FROM SEPARATE REACTIONS mechanism: d [B] / d t = + k 1 [A] - k 2 [B] Bio/Chemical Kinetics Made Easy 8

Software package DYNAFIT REFERENCES 1. Kuzmic P. (1996) Anal. Biochem. 237, 260 -273. “Program DYNAFIT for the analysis of enzyme kinetic data” 2. Kuzmic P. (2009) Meth. Enzymol. , 467, 247 -280. “DYNAFIT – A software package for enzymology” Bio/Chemical Kinetics Made Easy 9

A "Kinetic Compiler" HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 [ES] Rate equations: d[E ] / dt = - k 1 [E] [S] + k 2 [ES] + k 3 [ES] d[ES ] / dt = + k 1 [E] [S] - k 2 [ES] - k 3 [ES] Similarly for other species. . . Bio/Chemical Kinetics Made Easy 10

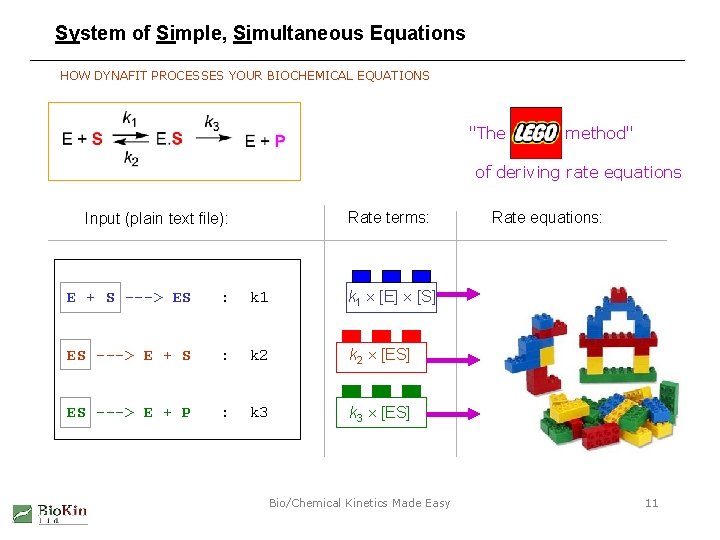
System of Simple, Simultaneous Equations HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS "The LEGO method" of deriving rate equations Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 [ES] Bio/Chemical Kinetics Made Easy Rate equations: 11

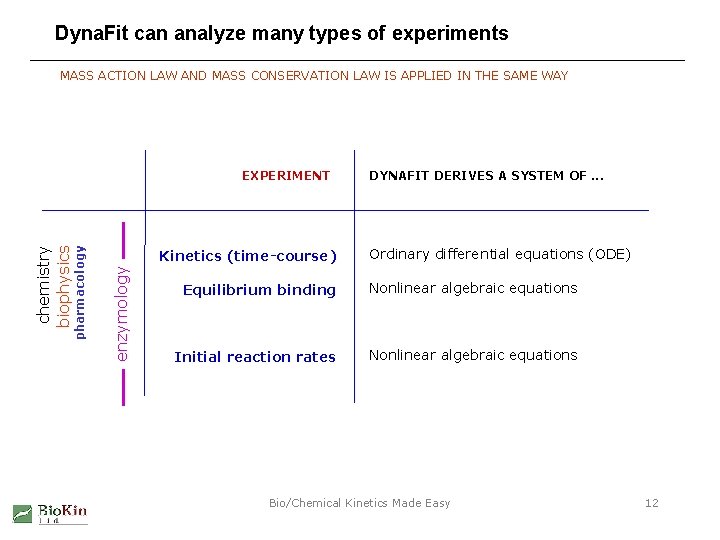
Dyna. Fit can analyze many types of experiments MASS ACTION LAW AND MASS CONSERVATION LAW IS APPLIED IN THE SAME WAY Kinetics (time-course) enzymology chemistry biophysics pharmacology EXPERIMENT DYNAFIT DERIVES A SYSTEM OF. . . Ordinary differential equations (ODE) Equilibrium binding Nonlinear algebraic equations Initial reaction rates Nonlinear algebraic equations Bio/Chemical Kinetics Made Easy 12

Biochemical / Biophysical Kinetics “Made Easy” Software DYNAFIT in drug discovery research Petr Kuzmič, Ph. D. Bio. Kin, Ltd. 1. Theory: differential equation models - DYNAFIT software 2. Example: lantha. Screen® Eu assay in “kinetic” mode - p 38 a kinase / antibody / tracer / desatinib Bio/Chemical Kinetics Made Easy

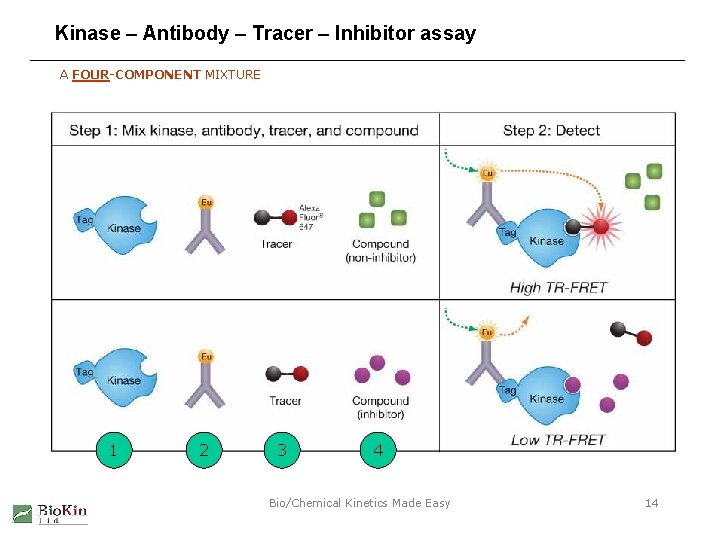
Kinase – Antibody – Tracer – Inhibitor assay A FOUR-COMPONENT MIXTURE 1 2 3 4 Bio/Chemical Kinetics Made Easy 14

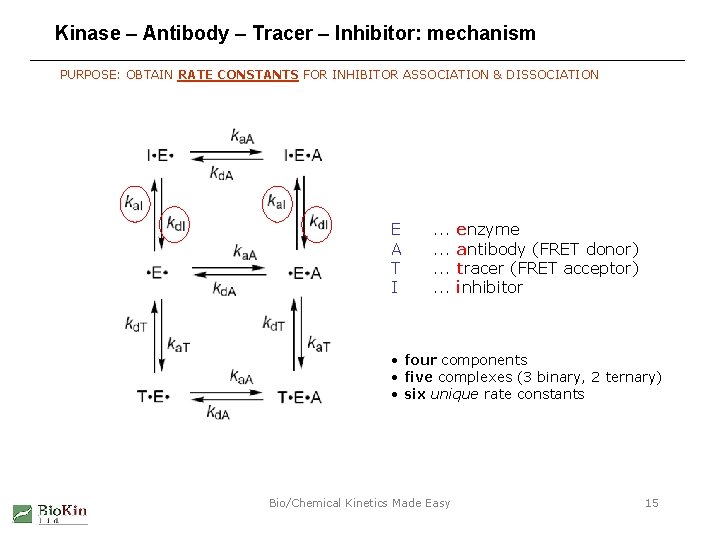
Kinase – Antibody – Tracer – Inhibitor: mechanism PURPOSE: OBTAIN RATE CONSTANTS FOR INHIBITOR ASSOCIATION & DISSOCIATION E A T I . . . enzyme antibody (FRET donor) tracer (FRET acceptor) inhibitor • four components • five complexes (3 binary, 2 ternary) • six unique rate constants Bio/Chemical Kinetics Made Easy 15

Rate constants and receptor-ligand residence time IS IT WORTH CHASING AFTER RATE CONSTANTS? Mbalaviele et al. (2009) J. Pharm. Exp. Ther. 329, 14 -25 “PHA-408 is an ATP competitive inhibitor, which binds IKK-2 tightly with a relatively slow off rate. ” Puttini et al. (2008) haematologica 93, 653 -61 “The present results suggest a slower off-rate (dissociation rate) of [a novel Abl kinase inhibitor] compared to imatinib as an explanation for the increased cellular activity of the former. ” Tummino & Copeland (2008) Biochemistry 47, 5481 -92 “. . . the extent and duration of responses to receptor-ligand interactions depend greatly on the time period over which the ligand is in residence on its receptor. ” Bio/Chemical Kinetics Made Easy 16

Let’s look at Kinase + Antibody + Tracer only. No Inhibitor yet. Bio/Chemical Kinetics Made Easy 17

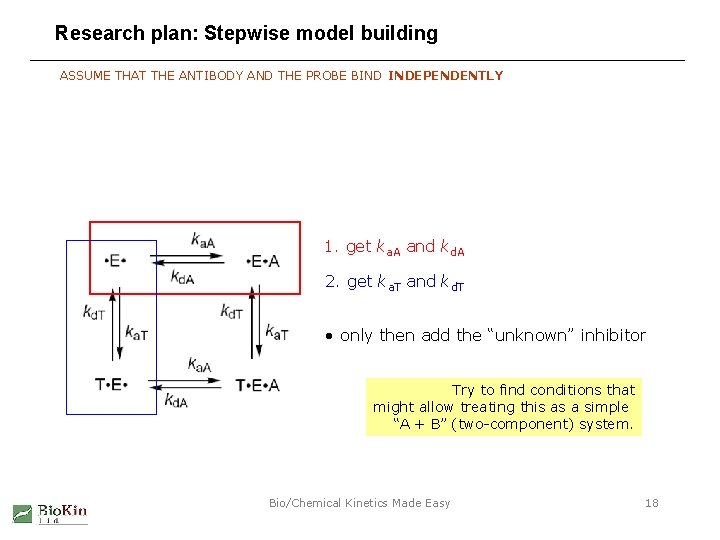
Research plan: Stepwise model building ASSUME THAT THE ANTIBODY AND THE PROBE BIND INDEPENDENTLY 1. get ka. A and kd. A 2. get ka. T and kd. T • only then add the “unknown” inhibitor Try to find conditions that might allow treating this as a simple “A + B” (two-component) system. Bio/Chemical Kinetics Made Easy 18

Classical method: “k(obs)” assuming [Antibody] >> [Kinase] GOODRICH & KUGEL (2006) “Binding and Kinetics for Molecular Biologists”, pages 91 -95 and k-1 Bio/Chemical Kinetics Made Easy 19

Enzyme + Antibody at very large excess of [Tracer] (pt. 1) THIS MIGHT ALLOW US TO TREAT THIS AS A SIMPLE “A + B” (TWO-COMPONENT) SYSTEM METHOD: 1. Incubate Tracer & Kinase - [Tracer] fixed, very large excess - [Kinase] varied 2. Wait 10 minutes to equilibrate exponential fit 3. Add [Antibody] k(obs) = 0. 0019 s-1 4. Measure increase in fluorescence (T. E. A) [E] = 1. 613 n. M [A] = 0. 2 n. M [T] = 200 n. M Bio/Chemical Kinetics Made Easy 20

Enzyme + Antibody at very large excess of [Tracer] (pt. 2) DYNAFIT INPUT “SCRIPT”: WE CAN USE SIMPLE ALGEBRAIC MODELS AS WELL [task] task = fit data = generic [parameters] t Ao, A, k [model] Ao = 0. 1 ? A = 1 ? k = 0. 001 ? F = Ao + A*(1 - exp(-k*t)) Bio/Chemical Kinetics Made Easy 21

Enzyme + Antibody at very large excess of [Tracer] (pt. 3) TRY TO FIT k(obs) TO THE STRAIGHT LINE MODEL EQUATION ? ! not a straight line Bio/Chemical Kinetics Made Easy 22

Enzyme + Antibody at very large excess of [Tracer] (pt. 4) POSSIBLE REASONS FOR THE NONLINEARITY OF k(app) VS. [Kinase] PLOT 1. [Kinase] is not at very large excess over [Antibody] at all times Goodrich & Kugel (2006), p. 95 2. Signal in Lantha. Screen® not strictly proportional to concentrations ? The “emission ratio” is calculated as the 665 nm signal divided by the 615 nm signal. 3. Kinase concentrations being “off” their nominal values ? Bio/Chemical Kinetics Made Easy 23

Enzyme + Antibody at very large excess of [Tracer] (pt. 5) GLOBAL FIT TO A MECHANISTIC MODEL [task] task = fit data = progress [mechanism] E + Ab <===> E. Ab : ka. A kd. A [constants] ka. A = 0. 001 ? kd. A = 0. 001 ? [concentrations] Ab = 0. 2 [responses] E. Ab = 3 ? [data]. . . file d 07 | concentration E = file d 06 | concentration E = file d 05 | concentration E =. . . 3. 1250 ? 1. 5625 ? 0. 7813 ? Bio/Chemical Kinetics Made Easy 24

Enzyme + Antibody at very large excess of [Tracer] (pt. 6) GLOBAL FIT TO A MECHANISTIC MODEL: BEST-FIT MODEL PARAMETERS k“on” = 0. 92 106 M-1 s-1 k“off” = 0. 00061 s-1 Kd = k“off” / k“on” = 0. 66 n. M Signal in Lantha. Screen® not strictly proportional to concentrations ? Bio/Chemical Kinetics Made Easy 25

Enzyme + Antibody at very large excess of [Tracer] (pt. 7) FIT AN “EQUILIBRIUM” BINDING MODEL TO END-OF-TRACE SIGNAL VALUES [task] [Kinase] task = fit data = equilibria [mechanism] E + Ab <===> E. Ab : Kd. A dissoc [constants] ; n. M Kd. A = 0. 7 ? . . . Kd. A = 0. 6 n. M Bio/Chemical Kinetics Made Easy 26

Enzyme + Antibody at very large excess of [Tracer] (pt. 8) SUMMARY RESULTS • Kinase–Antibody dissociation equilibrium constant is around 0. 7 n. M • The association rate constant is 0. 9 106 M-1 s-1 (“diffusion control”) • The half-time for dissociation is about 20 minutes (“slow”) CONCLUSIONS • At nanomolar concentrations of [Kinase] and [Antibody] there is always a mixture of all three species (E, Ab, E. Ab) • Diluting any kinase/antibody stock solution will cause the antibody to “fall off” the E. Ab complex • This “falling off” of the antibody will be slow, measured in minutes Bio/Chemical Kinetics Made Easy 27

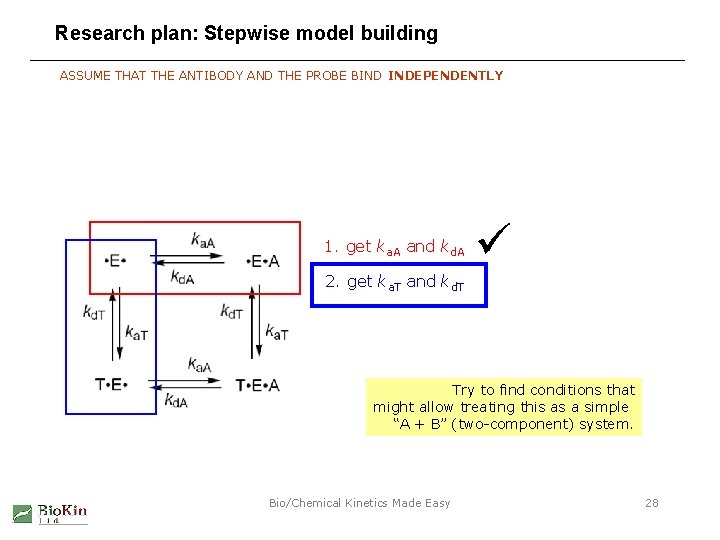
Research plan: Stepwise model building ASSUME THAT THE ANTIBODY AND THE PROBE BIND INDEPENDENTLY 1. get ka. A and kd. A 2. get ka. T and kd. T Try to find conditions that might allow treating this as a simple “A + B” (two-component) system. Bio/Chemical Kinetics Made Easy 28

Kinase - Antibody - Tracer: varied [Tracer] (pt. 1) RAW DATA 1. 2. 3. 4. 5 m. L 1. 5 n. M Kinase + 6 n. M Antibody 5 m. L solvent incubate 30 min Kinetics final Made Easy 5 m. L Bio/Chemical Tracer, varied concentration 29

Kinase - Antibody - Tracer: varied [Tracer] (pt. 1) RAW DATA: CLOSER LOOK AT HIGH [TRACER] CONCENTRATION ASSAY ? 1. 2. 3. 4. 5 m. L 1. 5 n. M Kinase + 6 n. M Antibody 5 m. L solvent incubate 30 min Kinetics Made Easy 5 m. L Bio/Chemical Tracer, 40 n. M final concentration 30

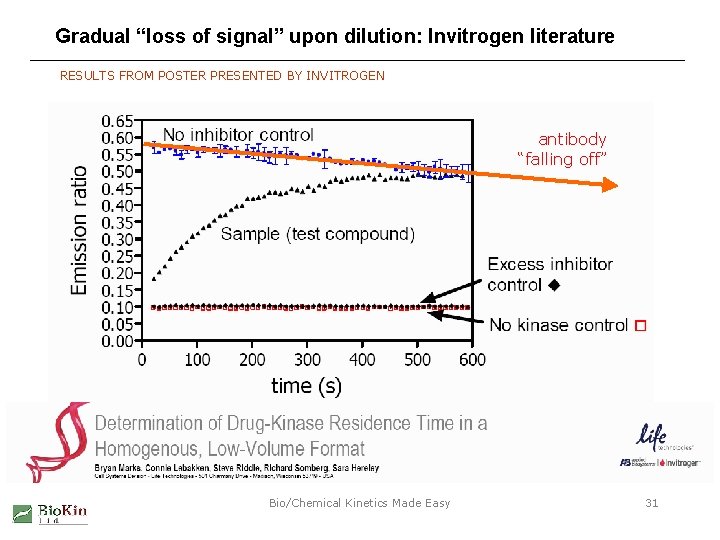
Gradual “loss of signal” upon dilution: Invitrogen literature RESULTS FROM POSTER PRESENTED BY INVITROGEN antibody “falling off” Bio/Chemical Kinetics Made Easy 31

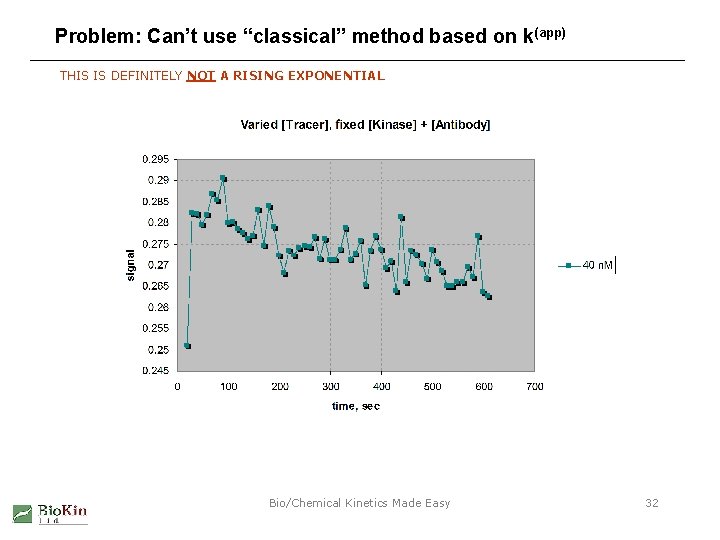
Problem: Can’t use “classical” method based on k(app) THIS IS DEFINITELY NOT A RISING EXPONENTIAL Bio/Chemical Kinetics Made Easy 32

Solution: Global fit of both sets of experiments (pt. 1) EXPERIMENT #1: VARIED [TRACER] [A] = 2 n. M [E] = 0. 5 n. M [T] = 0. 4. . . 40 n. M EXPERIMENT #2: VARIED [ KINASE] [A] = 0. 2 n. M [E] = 0. 098. . . 3. 13 n. M [T] = 200 n. M Bio/Chemical Kinetics Made Easy 33

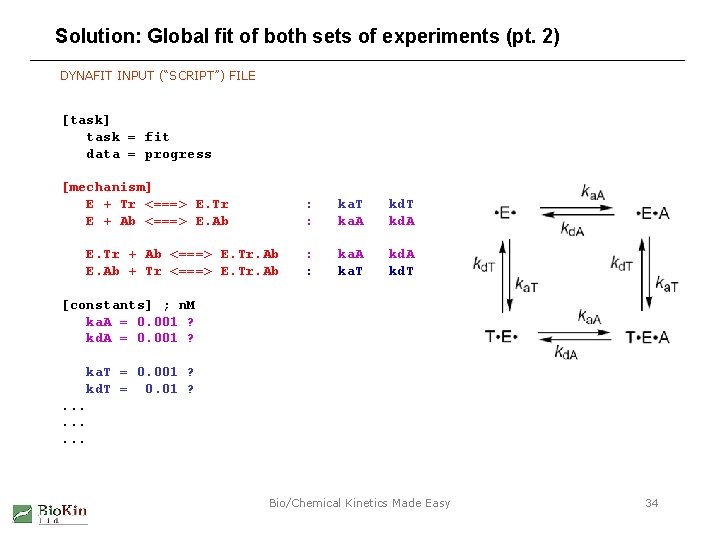
Solution: Global fit of both sets of experiments (pt. 2) DYNAFIT INPUT (“SCRIPT”) FILE [task] task = fit data = progress [mechanism] E + Tr <===> E. Tr E + Ab <===> E. Ab E. Tr + Ab <===> E. Tr. Ab E. Ab + Tr <===> E. Tr. Ab : : ka. T ka. A kd. T kd. A : : ka. A ka. T kd. A kd. T [constants] ; n. M ka. A = 0. 001 ? kd. A = 0. 001 ? ka. T = 0. 001 ? kd. T = 0. 01 ? . . Bio/Chemical Kinetics Made Easy 34

Solution: Global fit of both sets of experiments (pt. 3) DYNAFIT OUTPUT: BEST-FIT PARAMETERS k“on”T = 2. 7 106 M-1 s-1 k“off”T = 0. 021 s-1 Kd. T = 7. 9 n. M k“on”A = 0. 92 106 M-1 s-1 k“off”A = 0. 00061 s-1 Kd. A = 0. 66 n. M CONCLUSIONS • Tracer is tight binding but “not that tight”: It will be impossible to completely prevent inhibitor rebinding by competition. • Tracer is relatively “fast off” but “not that fast” (t 1/2 = 0. 5 min): In certain experiments there could transients due to tracer interactions. • It’s a fairly complicated system: Once inhibitor is added all six rate constants need to be considered. Bio/Chemical Kinetics Made Easy 35

Now for the complete four-component system: Kinase + Antibody + Tracer + Inhibitor Bio/Chemical Kinetics Made Easy 36

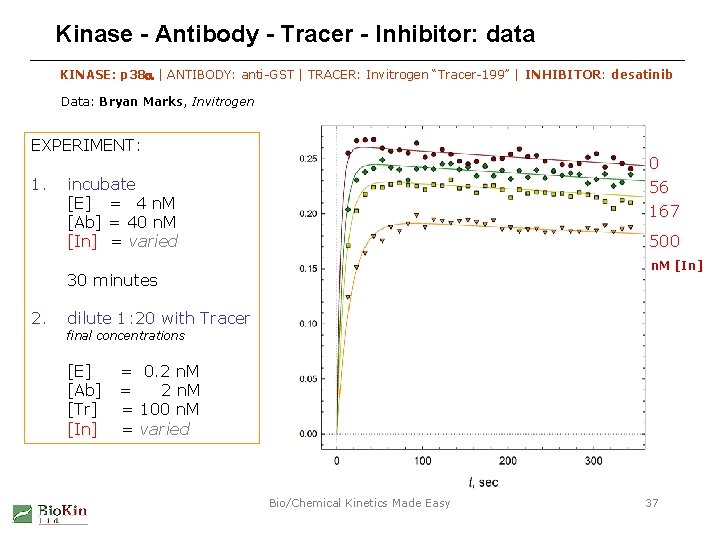
Kinase - Antibody - Tracer - Inhibitor: data KINASE: p 38 a | ANTIBODY: anti-GST | TRACER: Invitrogen “Tracer-199” | INHIBITOR: desatinib Data: Bryan Marks, Invitrogen EXPERIMENT: 1. 0 incubate [E] = 4 n. M [Ab] = 40 n. M [In] = varied 56 167 500 n. M [In] 30 minutes 2. dilute 1: 20 with Tracer final concentrations [E] [Ab] [Tr] [In] = 0. 2 n. M = 100 n. M = varied Bio/Chemical Kinetics Made Easy 37

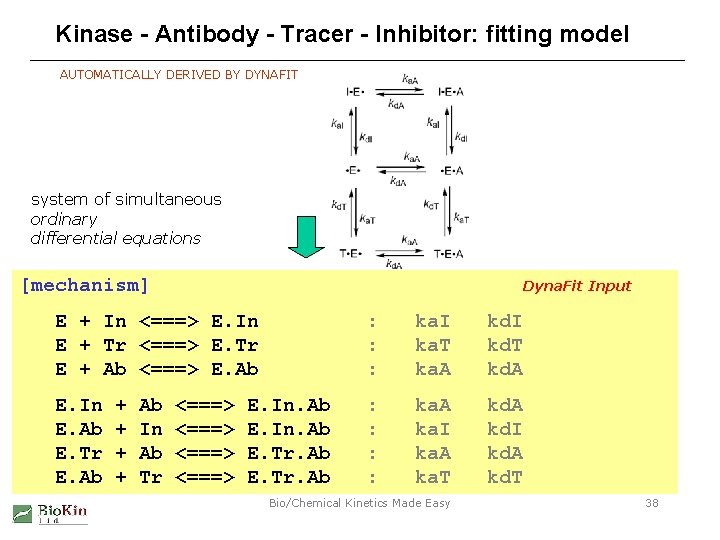
Kinase - Antibody - Tracer - Inhibitor: fitting model AUTOMATICALLY DERIVED BY DYNAFIT system of simultaneous ordinary differential equations [mechanism] Dyna. Fit Input d[E]/dt = - ka. I[E][In] + kd. I[E. In] - ka. T[E][Tr] + kd. T[E. Tr] - ka. A[E][Ab] + kd. A[E. Ab] d[In]/dt ka. I[E][In] + kd. I[E. In] - ka. I[E. Ab][In] + kd. I: [E. In. Ab] E += -In <===> E. In ka. I kd. I d[E. In]/dt = + ka. I<===> [E][In] - kd. IE. Tr [E. In] - ka. A[E. In][Ab] +: kd. A[E. In. Ab] E + Tr ka. T kd. T d[Tr]/dt = - ka. T[E][Tr] + kd. T[E. Tr] - ka. T[E. Ab][Tr] + kd. T[E. Tr. Ab] E + Ab <===> E. Ab : ka. A kd. A d[E. Tr]/dt = + ka. T[E][Tr] - kd. T[E. Tr] - ka. A[E. Tr][Ab] + kd. A[E. Tr. Ab] d[Ab]/dt = - ka. A[E][Ab] + kd. A[E. Ab] - ka. A[E. In][Ab] + kd. A[E. In. Ab] - ka. A[E. Tr][Ab] + kd. A[E. Tr. Ab] E. In + Ab <===> E. In. Ab : ka. A kd. A d[E. Ab]/dt = + ka. A[E][Ab] - kd. A[E. Ab] - ka. I[E. Ab][In] + kd. I[E. In. Ab] - ka. T[E. Ab][Tr] + kd. T[E. Tr. Ab] E. Ab += In <===> -E. In. Ab ka. I kd. I d[E. In. Ab]/dt + ka. A[E. In][Ab] kd. A[E. In. Ab] + ka. I: [E. Ab][In] - kd. I[E. In. Ab] E. Tr + = Ab <===> E. Tr. Ab : [E. Ab][Tr] ka. A- kd. T[E. Tr. Ab] kd. A d[E. Tr. Ab]/dt + ka. A[E. Tr][Ab] - kd. A[E. Tr. Ab] + ka. T E. Ab + Tr <===> E. Tr. Ab : ka. T Bio/Chemical Kinetics Made Easy kd. T 38

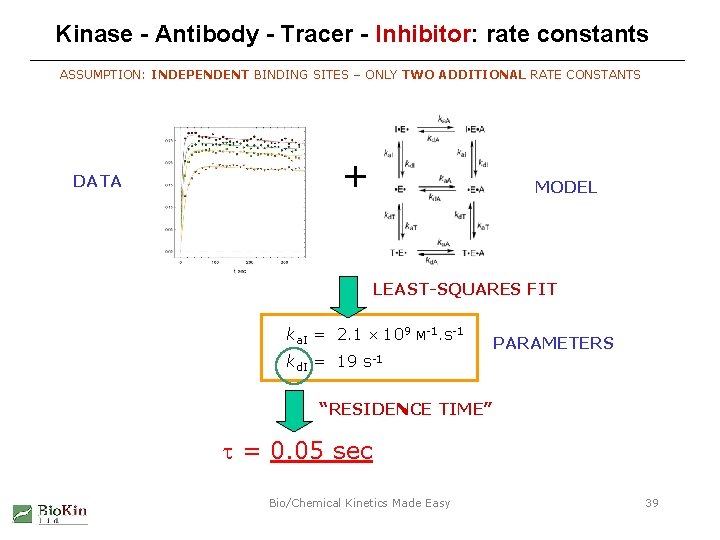
Kinase - Antibody - Tracer - Inhibitor: rate constants ASSUMPTION: INDEPENDENT BINDING SITES – ONLY TWO ADDITIONAL RATE CONSTANTS DATA + MODEL LEAST-SQUARES FIT ka. I = 2. 1 109 kd. I = 19 M-1. s-1 PARAMETERS “RESIDENCE TIME” t = 0. 05 sec Bio/Chemical Kinetics Made Easy 39

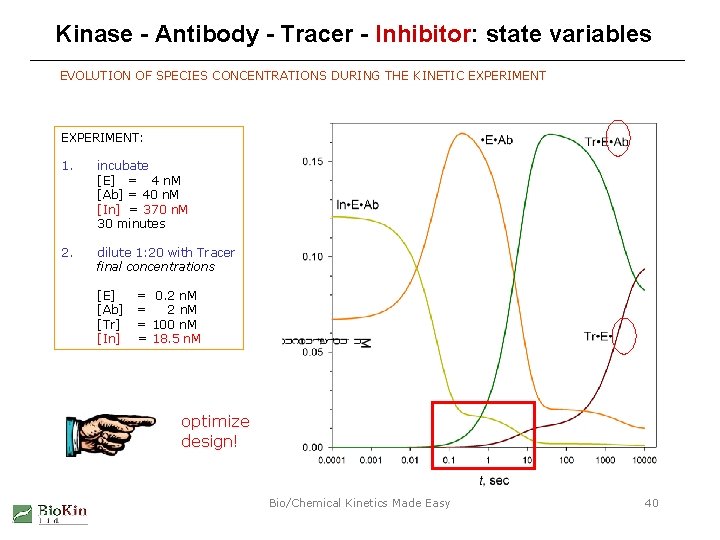
Kinase - Antibody - Tracer - Inhibitor: state variables EVOLUTION OF SPECIES CONCENTRATIONS DURING THE KINETIC EXPERIMENT: 1. incubate [E] = 4 n. M [Ab] = 40 n. M [In] = 370 n. M 30 minutes 2. dilute 1: 20 with Tracer final concentrations [E] [Ab] [Tr] [In] = 0. 2 n. M = 100 n. M = 18. 5 n. M optimize design! Bio/Chemical Kinetics Made Easy 40

Acknowledgments • Bryan Marks: all kinase experiments Invitrogen, a. k. a. Life Technologies, Madison, Wisconsin Bio/Chemical Kinetics Made Easy 41

Questions ? http: //www. biokin. com Bio/Chemical Kinetics Made Easy 42