Chapter 13 Kinetics of A Particle Force and

Chapter 13 : Kinetics of A Particle – Force and acceleration

Newton’s Law of Motion First Law: A particle originally at rest, or moving in a straight line with a constant velocity, will remain in this state provided the particle is not subjected to an unbalanced force. Second Law: A particle acted upon by an unbalanced force F experiences an acceleration a that has the same direction as the force and a magnitude that is directly proportional to the force. © 2007 Pearson Education South Asia Pte Ltd

Newton’s Law of Motion Third Law: The mutual forces of action and reaction between two particles are equal, opposite and collinear. Equation of motion: F = ma Newton’s Law of Gravitational Attraction. A law governing the mutual attractive gravitational force acting between them. © 2007 Pearson Education South Asia Pte Ltd

Newton’s Law of Motion Mass and Weight. Mass is a property of matter by which we can compare the response of one body with that of another. It is an absolute quantity since the measurement can be made at any location. Weight of a body is not absolute since it is measured in a gravitational field, hence its magnitude depends on the location measured. © 2007 Pearson Education South Asia Pte Ltd

Newton’s Law of Motion SI System of Units. The mass of the body is specified in kilograms and the weight must be calculated using the equation of motion, F = ma W = mg (N) (g = 9. 81 m/s 2) © 2007 Pearson Education South Asia Pte Ltd

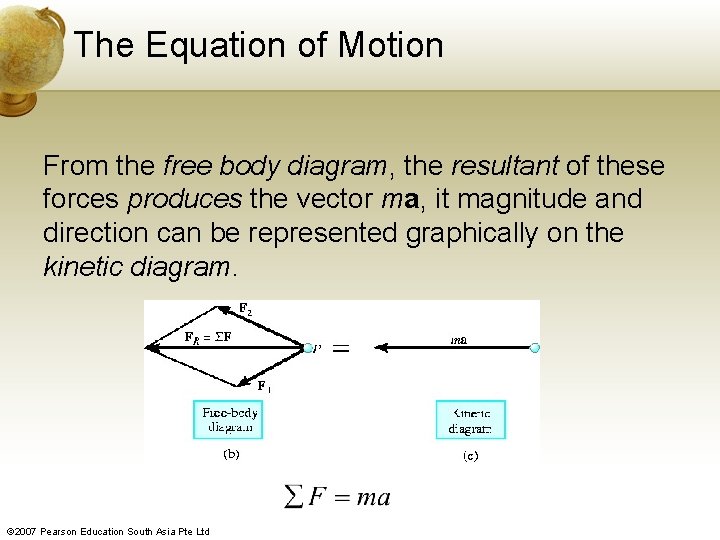
The Equation of Motion The equation of motion may be written as Consider particle P of mass m and subjected to the action of two forces, F 1 and F 2. © 2007 Pearson Education South Asia Pte Ltd

The Equation of Motion From the free body diagram, the resultant of these forces produces the vector ma, it magnitude and direction can be represented graphically on the kinetic diagram. © 2007 Pearson Education South Asia Pte Ltd

The Equation of Motion Note that if FR = ΣF = 0, then acceleration is zero, so that the particle will either remain at rest or moves along a straight line with a constant velocity. Such a condition is called static equilibrium, Newton’s First Law of Motion © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion for a System of Particles • Consider a system of n particles isolated within an enclosed region in space. • Arbitrary ith particle having a mass of mi is subjected to a system of internal forces which resultant force is represented by fi and a resultant external force Fi. © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion for a System of Particles • The free body diagram for the ith particle are shown. Applying equation of motion yields ΣF = ma; F i + fi = m i a i • If equation of motion is applied to each of the other particles, these equations can be added together vectorially, ΣFi + Σ fi = Σmiai © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion for a System of Particles • Since internal forces between particles all occur in equal but opposite collinear pairs, the summation of these internal forces will equal zero. ΣFi = Σmiai • If r. G is a position vector which locates the center of mass G of the particles, then mr. G = Σmiri where m = Σmi is the total mass of all the particles • Differentiating twice w. r. t time yields ma. G = Σmiai © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion for a System of Particles • Therefore, ΣF = ma. G • The sum of the external forces acting on the system of particles is equal to the total mass of the particles times the acceleration of its center of mass G. © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion: Rectangular Coordinates • When a particle is moving relative to an inertial x, y, z frame of reference, the forces acting on the particle, and its acceleration may be expressed in term of their i, j, k components ΣF = ma ΣFxi + ΣFyj + ΣFzk = m(axi + ayj + azk) © 2007 Pearson Education South Asia Pte Ltd

Equation of Motion: Rectangular Coordinates • We may write the following three scalar equations: © 2007 Pearson Education South Asia Pte Ltd

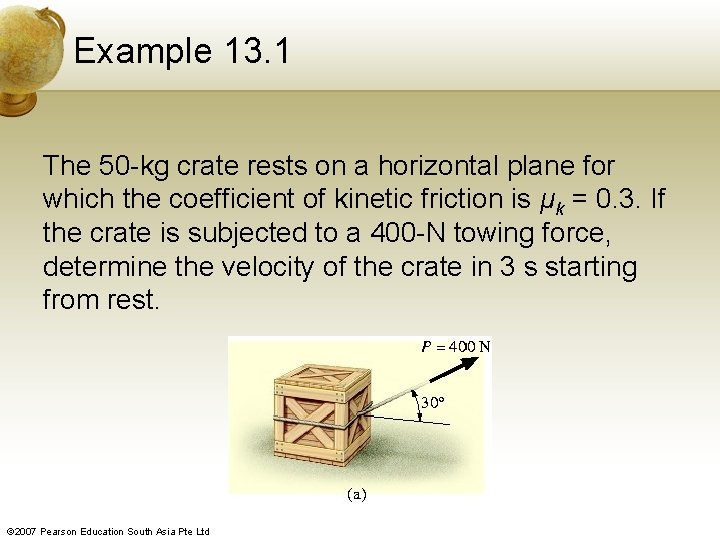
Example 13. 1 The 50 -kg crate rests on a horizontal plane for which the coefficient of kinetic friction is μk = 0. 3. If the crate is subjected to a 400 -N towing force, determine the velocity of the crate in 3 s starting from rest. © 2007 Pearson Education South Asia Pte Ltd

Example 13. 1 Free-Body Diagram. The weight of the crate is W = mg = 50 (9. 81) = 490. 5 N. The frictional force has a magnitude F = μk. NC and acts to the left, since it opposes the motion of the crate. The acceleration a is assumed to act horizontally, in the positive x direction. There are 2 unknowns, namely NC and a. © 2007 Pearson Education South Asia Pte Ltd

Example 13. 1 Equations of Motion. Solving for the two equations yields © 2007 Pearson Education South Asia Pte Ltd

Example 13. 1 Kinematics. Acceleration is constant, since the applied force P is constant. Initial velocity is zero, the velocity of the crate in 3 s is © 2007 Pearson Education South Asia Pte Ltd

Equations of Motion: Normal and Tangential Coordinates When a particle moves over a curved path which is known, the equation of motion for the particle may be written in the tangential, normal and binormal directions. We have ΣF = ma ΣFtut + ΣFnun + ΣFbub = mat +man Here ΣFt, ΣFn, ΣFb represent the sums of all the force components acting on the particle in the tangential, normal and binormal directions. © 2007 Pearson Education South Asia Pte Ltd

Equations of Motion: Normal and Tangential Coordinates Since the particle is constrained to move along the path, there is no motion in the binormal direction © 2007 Pearson Education South Asia Pte Ltd

Equations of Motion: Normal and Tangential Coordinates • at (=dv/dt) represents the time rate of change in the magnitude of velocity • Therefore if ΣFt acts in the direction of motion, the particle’s speed will increase. If it acts in the opposite direction, the particle will slow down. • an (=v 2/ρ) represents the time rate of change in the velocity’s direction. © 2007 Pearson Education South Asia Pte Ltd

Equations of Motion: Normal and Tangential Coordinates • Since this vector always acts in the positive n direction, i. e. toward the path’s center of curvature, then ΣFn, which causes an, also act in this direction. © 2007 Pearson Education South Asia Pte Ltd

Example 13. 6 & 13. 8 © 2007 Pearson Education South Asia Pte Ltd