Unit 6 Radical and Rational Functions Roots and











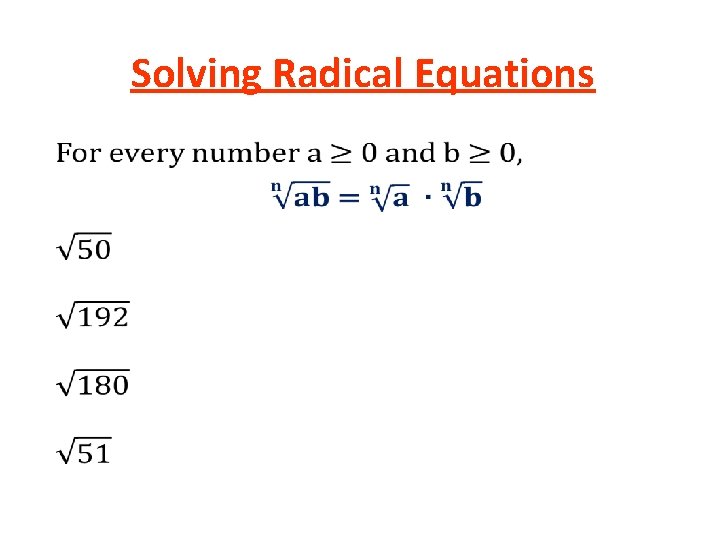














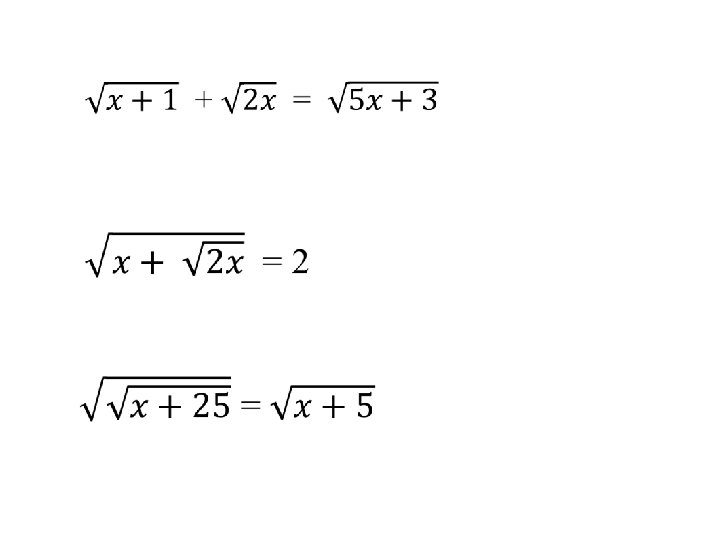


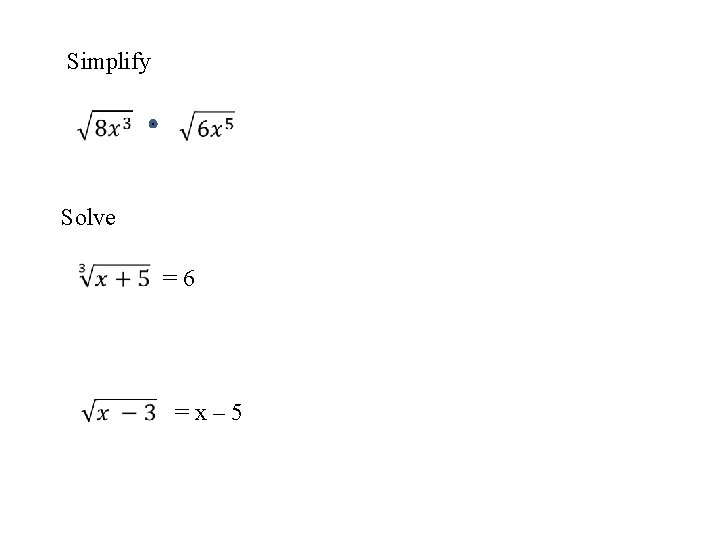
































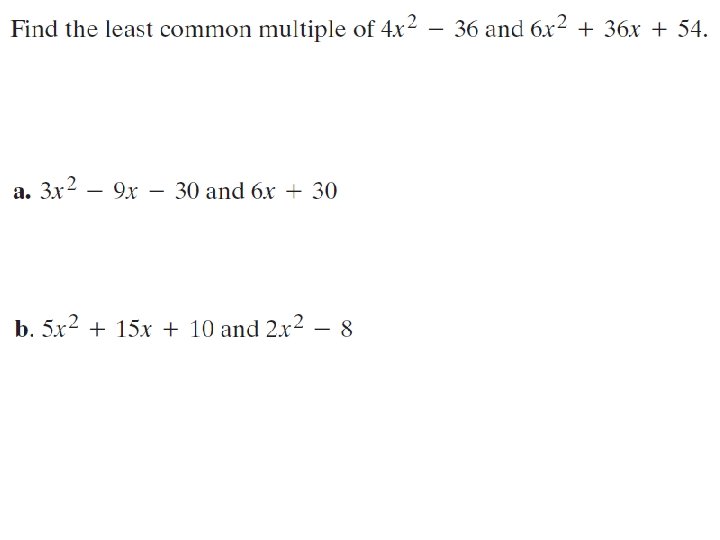
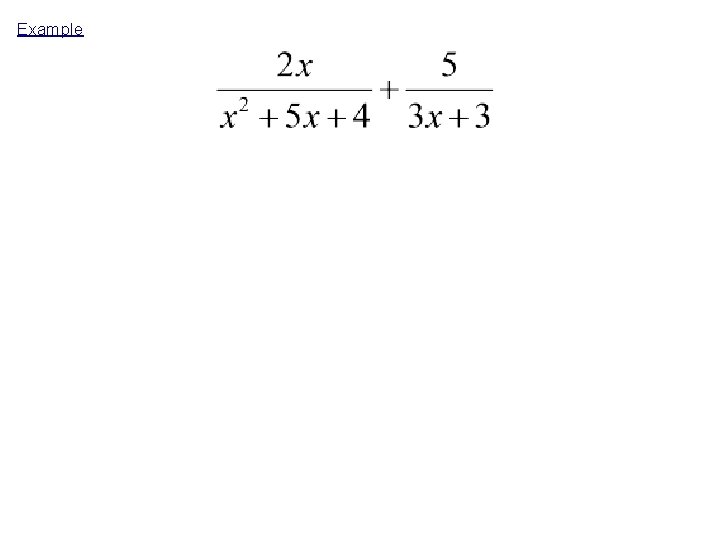
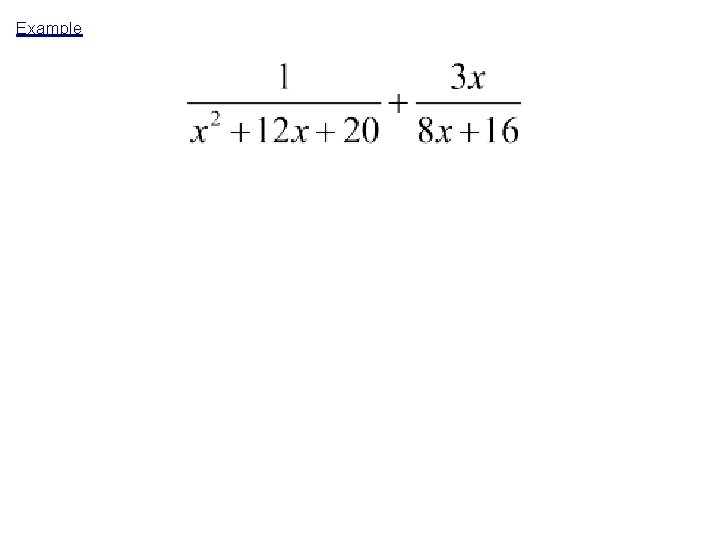

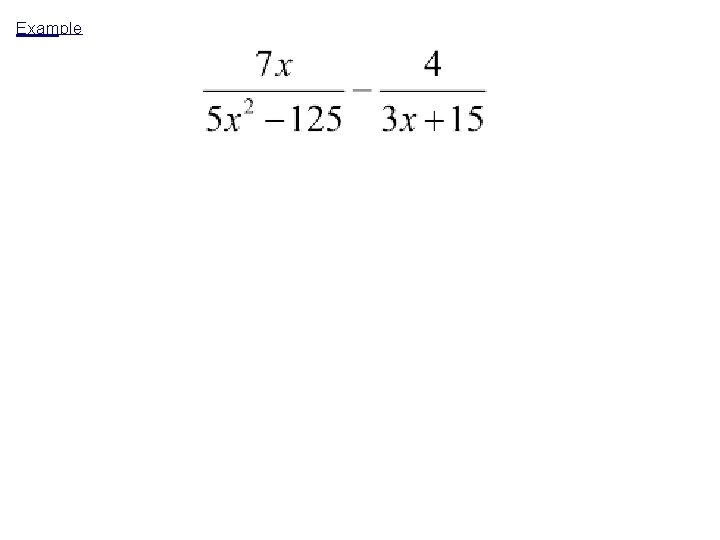

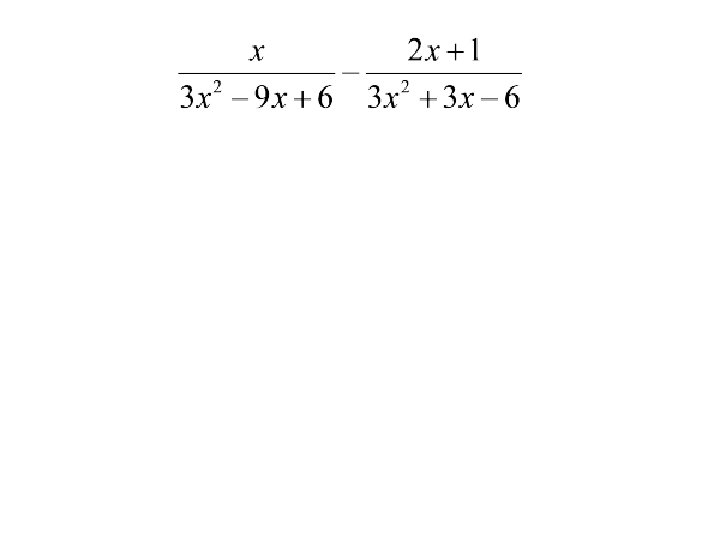


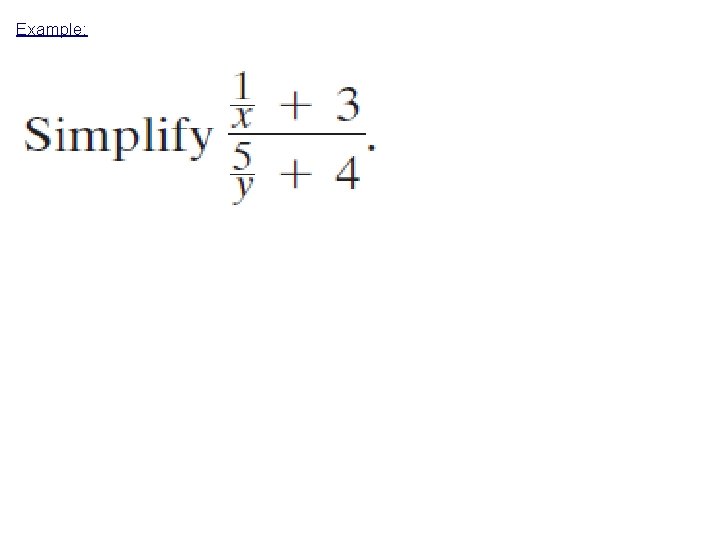
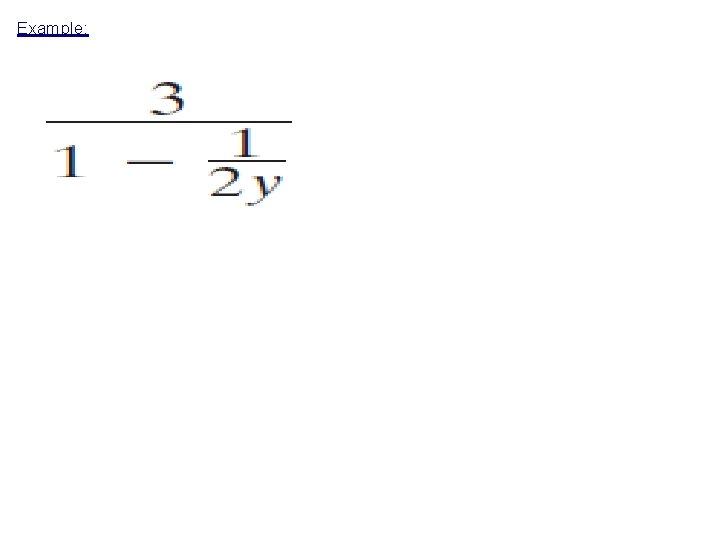



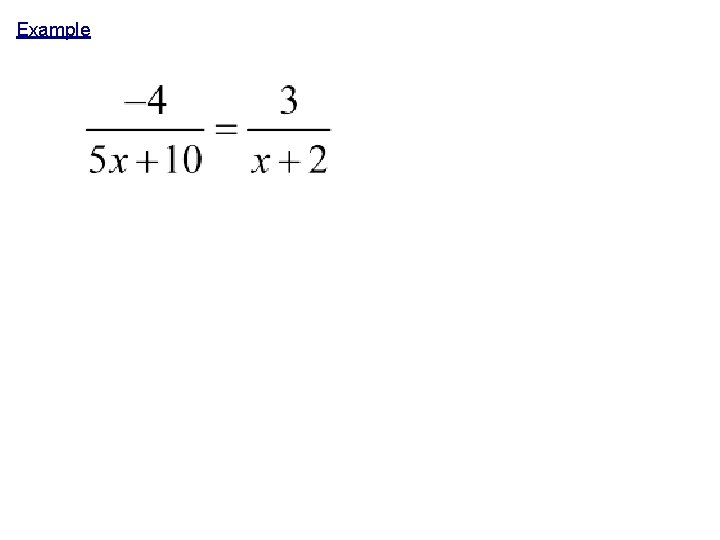
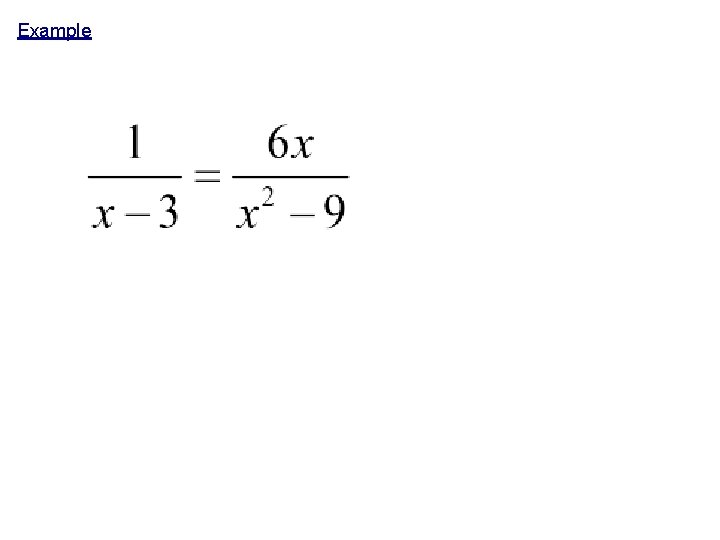
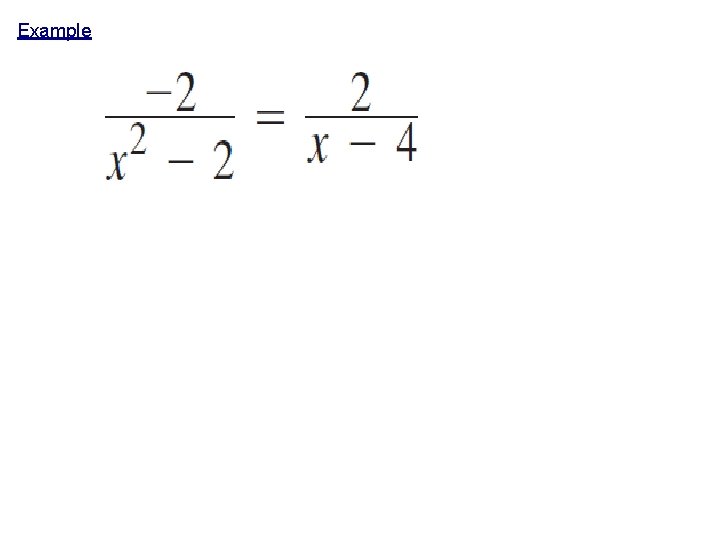

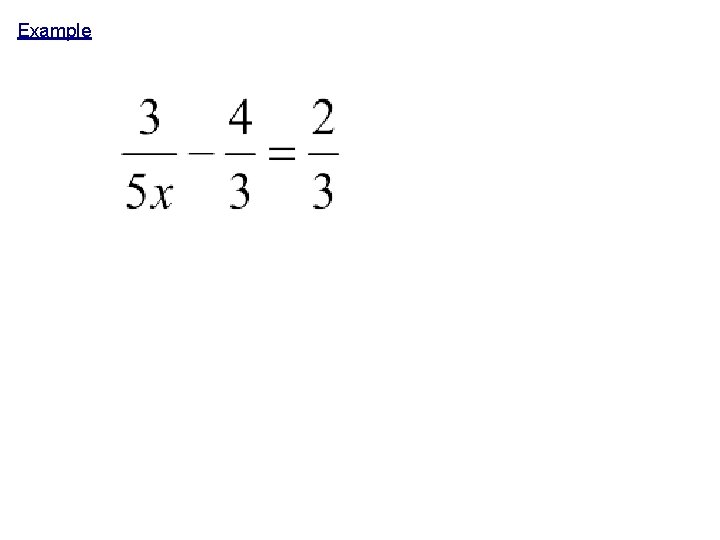
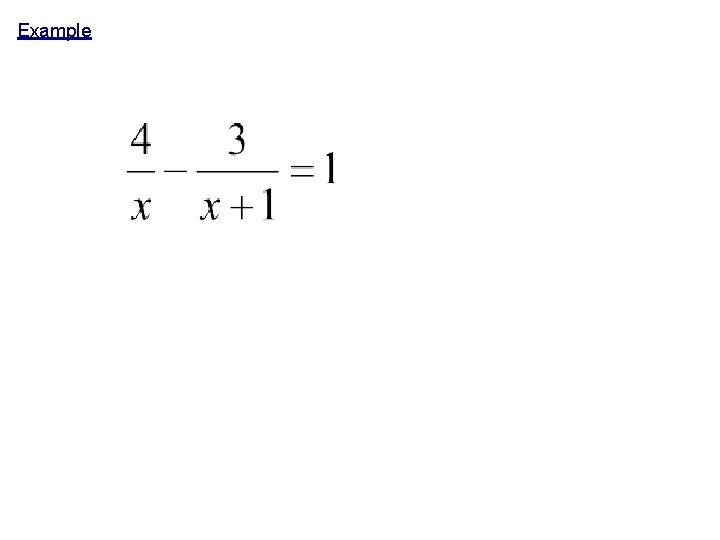
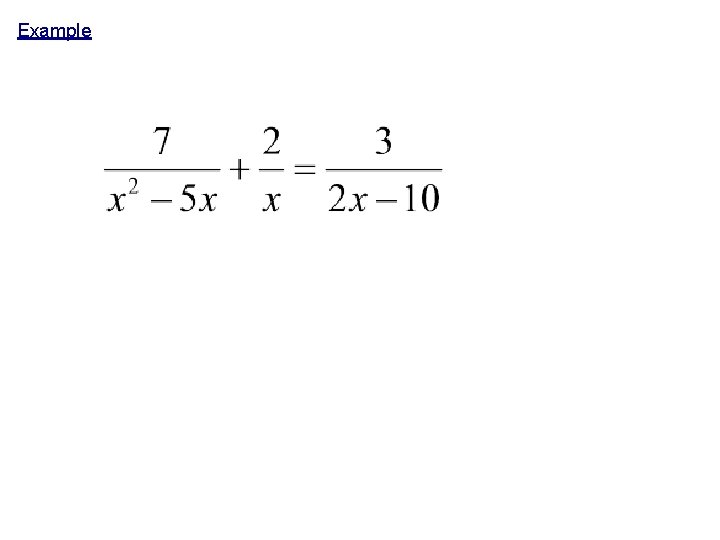
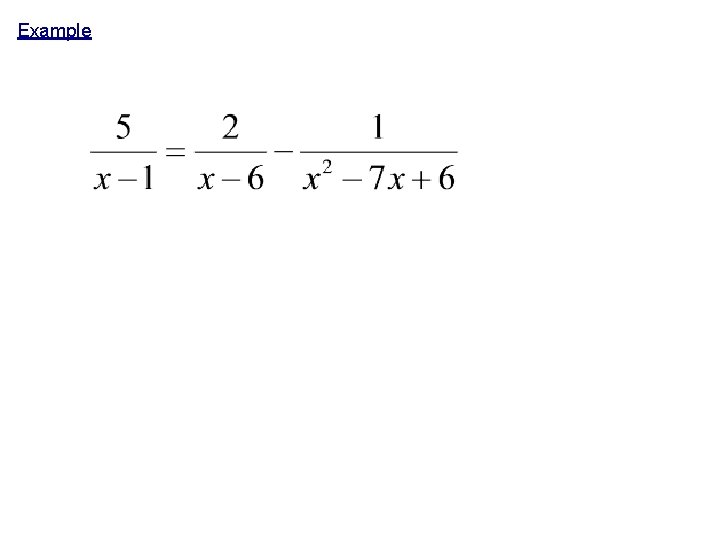
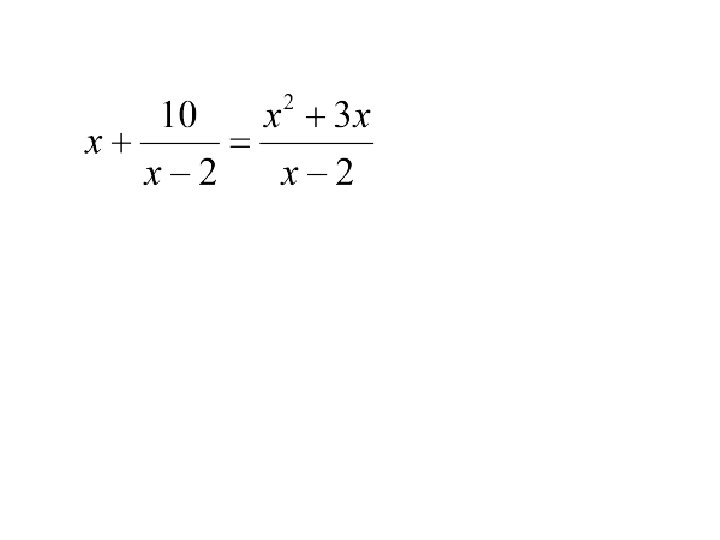








- Slides: 117

Unit 6: “Radical and Rational Functions” Roots and Radical Expressions Objective: To evaluate and simplify radical expressions. nth root – For any real number a, b, and positive integer n, if an = b, then “a is the nth root of b”. Example: Since 43 = 64, then “ 4 is the 3 rd root of 64” v. A radical is used to indicate a root.

Evaluating Radicals •

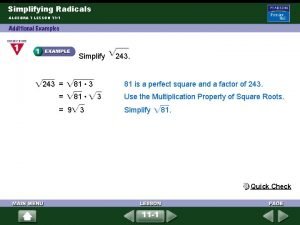
Simplifying Radicals •

Simplifying Radicals •

Simplifying Radicals with Variables •

Simplifying Radicals with Variables •

Multiply Two Radicals •

Multiply Two Radicals •

End of Day 1 P 366 #13 – 16, #39 – 46 P 371 #17 - 22

Solving Radical Equations •

Solving Radical Equations •
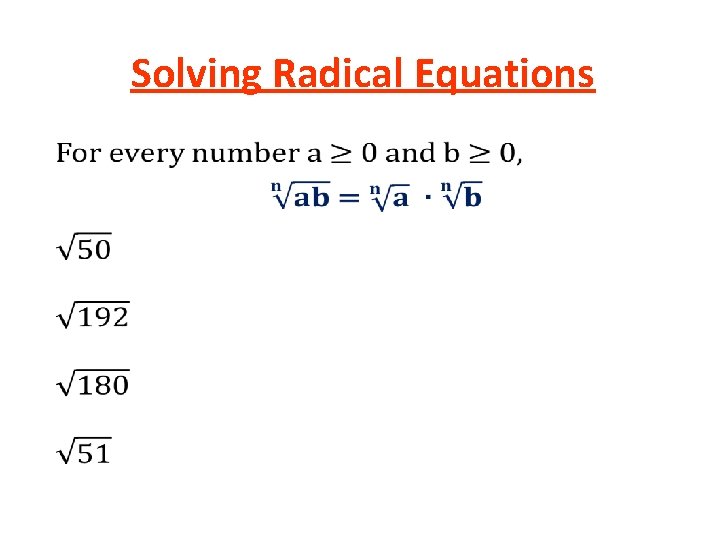
Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

Solving Radical Equations* •

End of Day 2
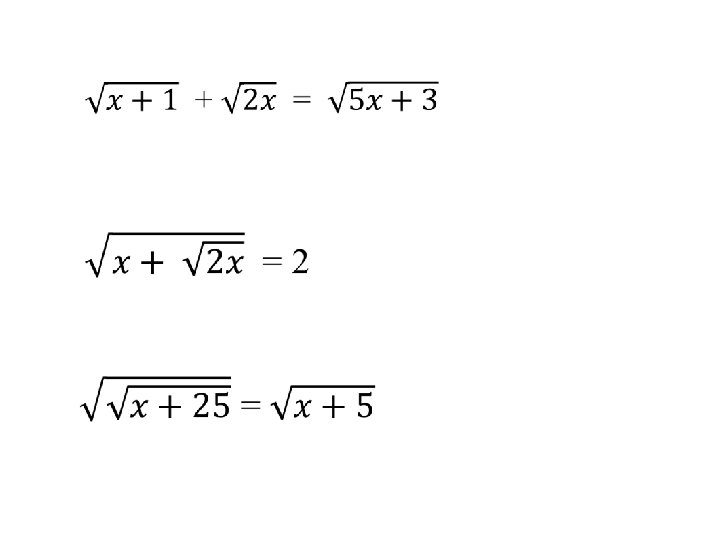

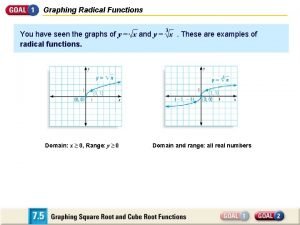
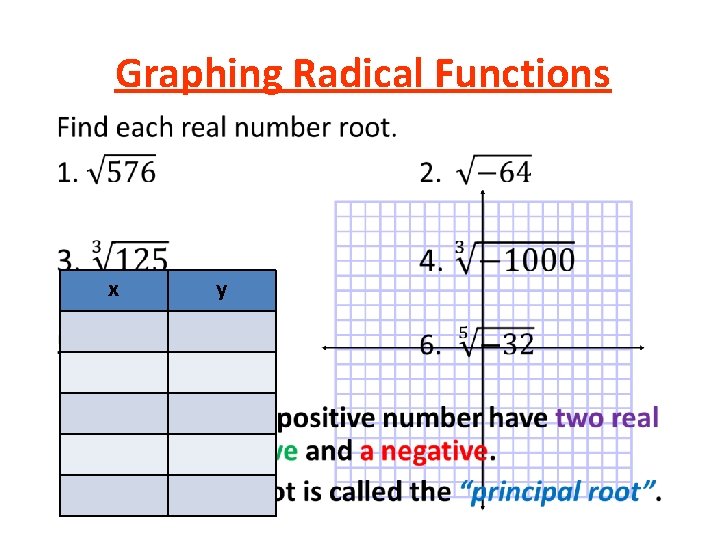
Graphing Radical Functions • x y

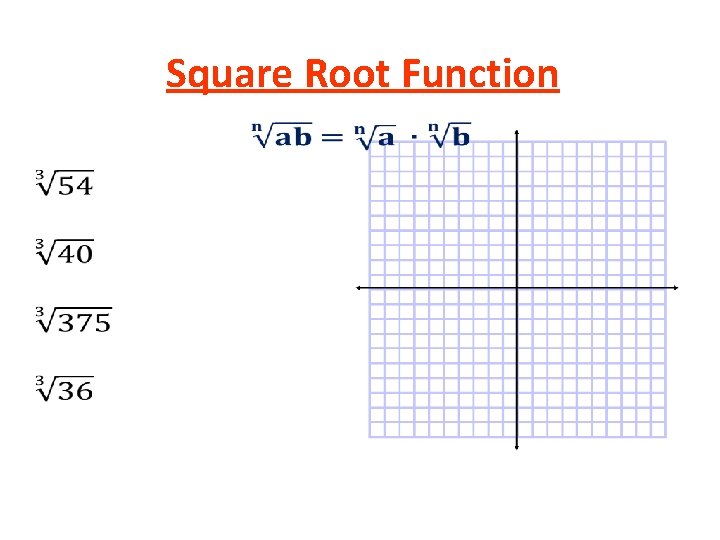
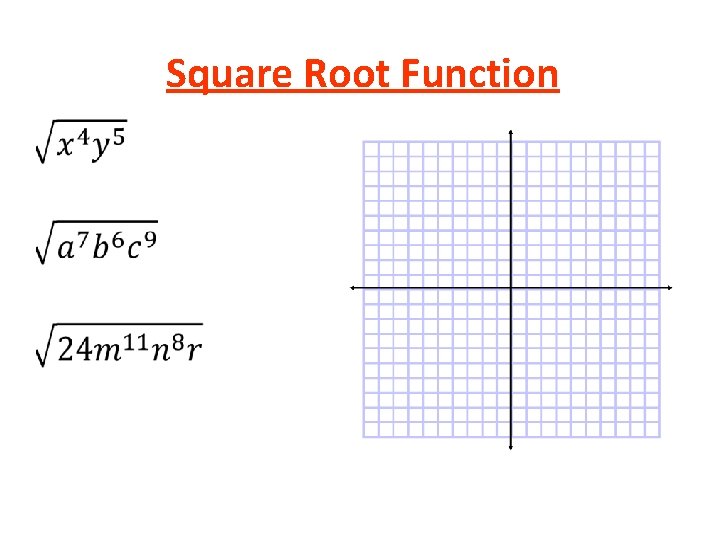
Square Root Function •

Square Root Function •

Square Root Function •

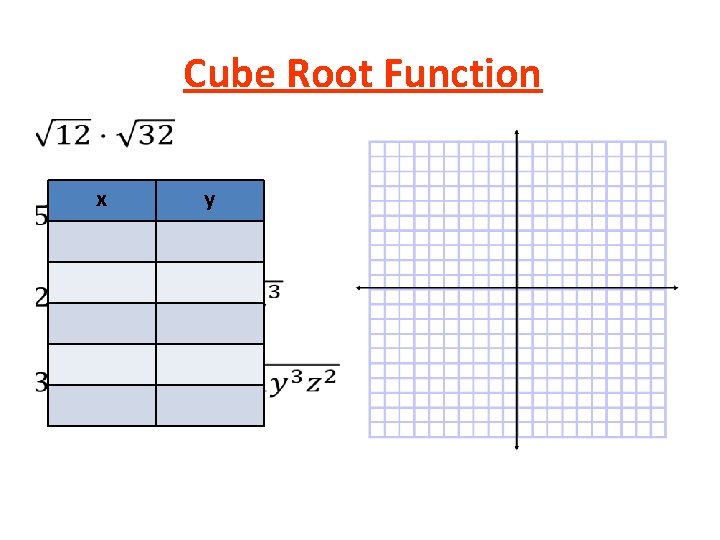
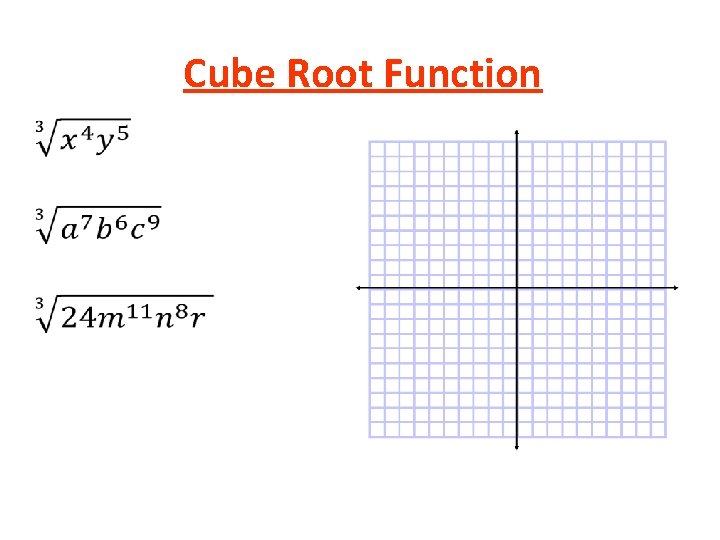
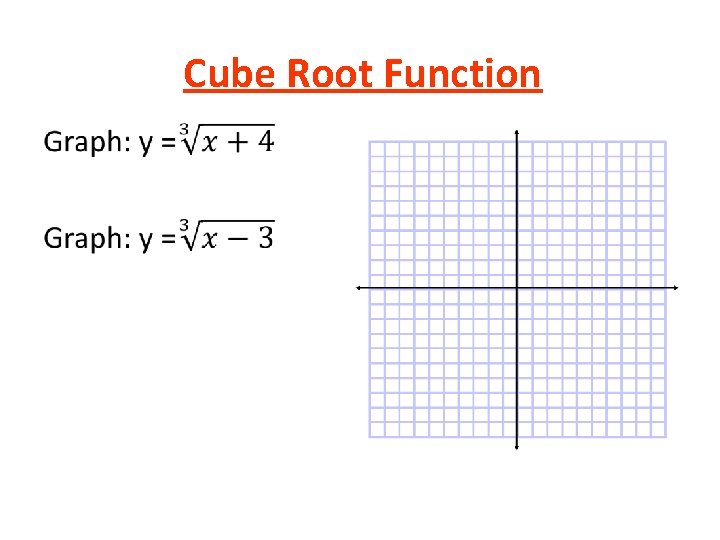
Cube Root Function • x y

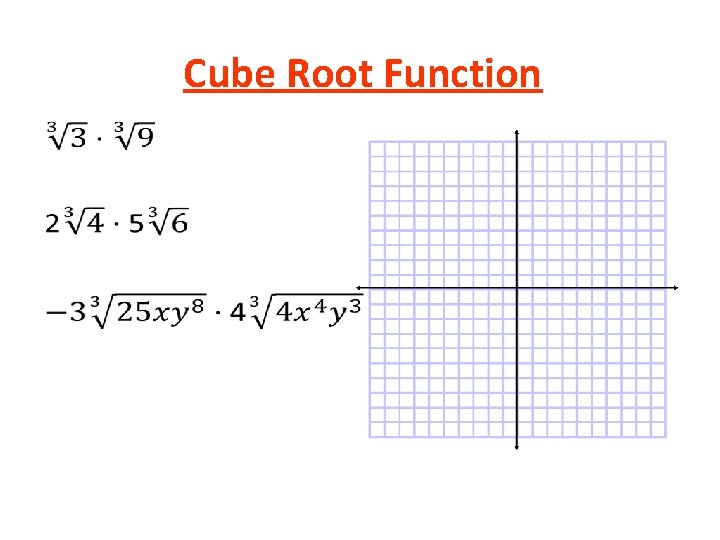
Cube Root Function •

Cube Root Function •

Cube Root Function •

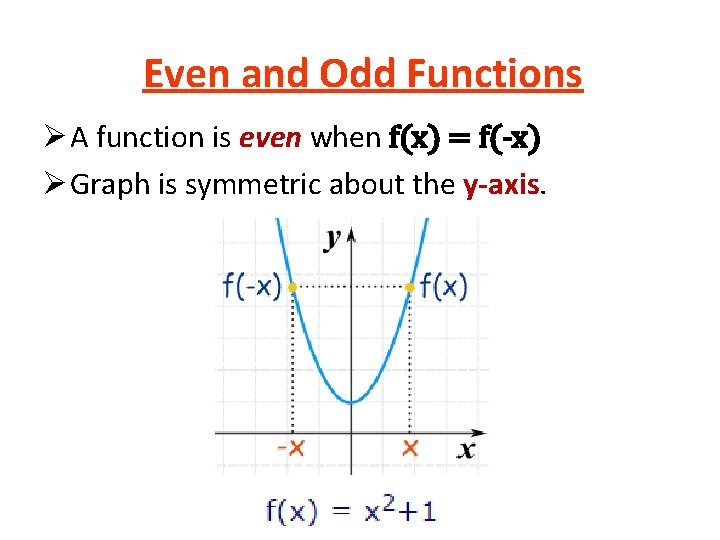
Even and Odd Functions Ø A function is even when f(x) = f(-x) Ø Graph is symmetric about the y-axis.

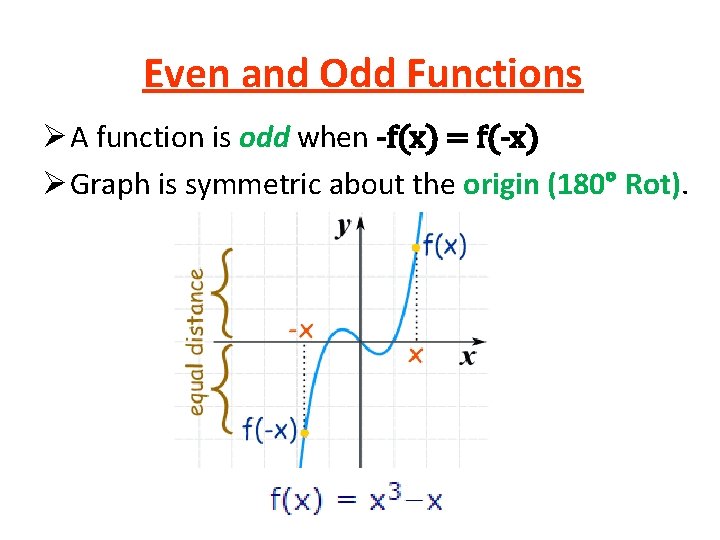
Even and Odd Functions Ø A function is odd when -f(x) = f(-x) Ø Graph is symmetric about the origin (180° Rot).

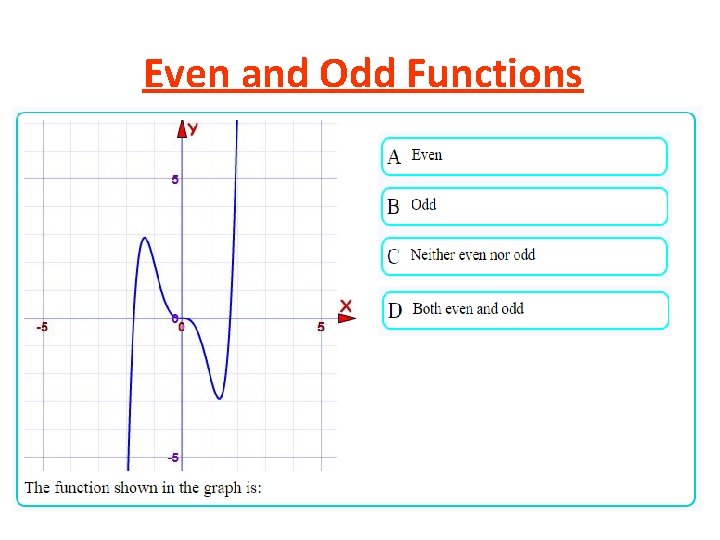
Even and Odd Functions

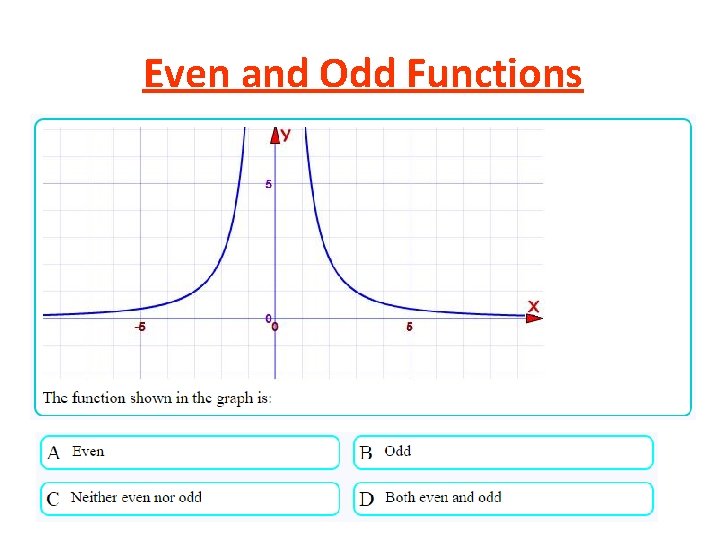
Even and Odd Functions

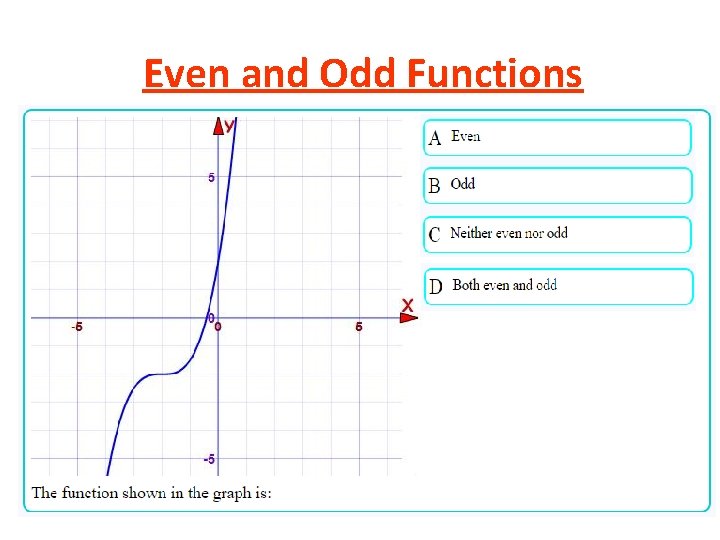
Even and Odd Functions

Even and Odd Functions

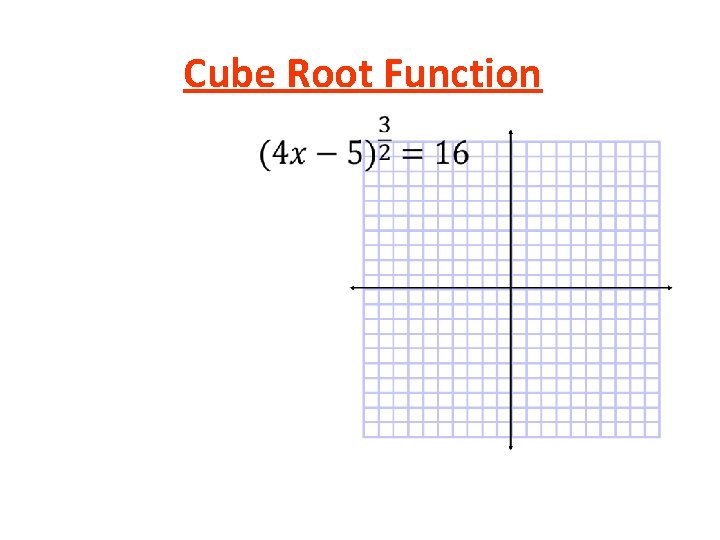
Cube Root Function •
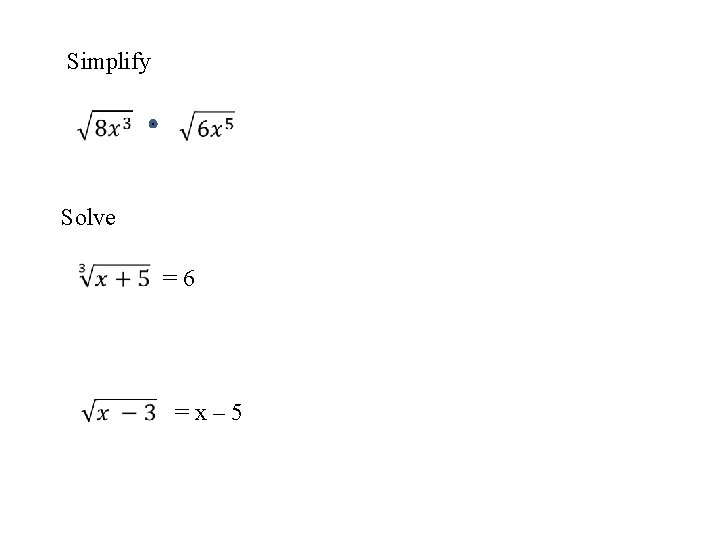
Simplify Solve =6 =x– 5

Unit 6 "Radical and Rational Functions" Title: Inverse Variation Introduction to Rational Functions Objective: To identify and use inverse variation and combined variation.

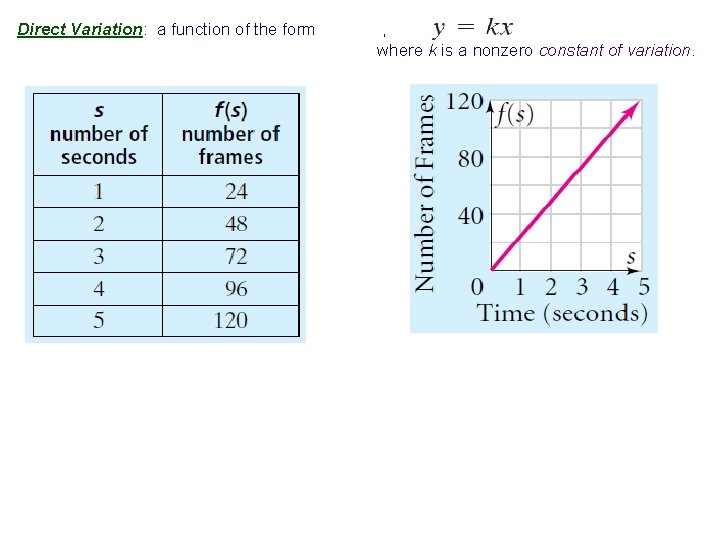
Direct Variation: a function of the form , where k is a nonzero constant of variation.

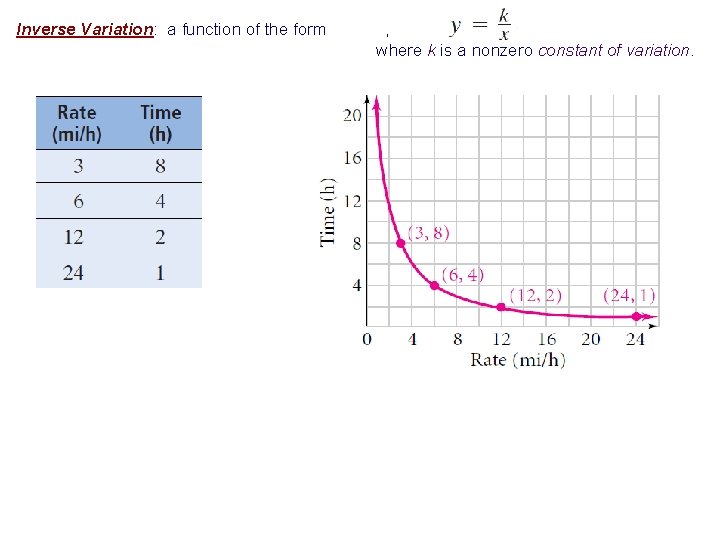
Inverse Variation: a function of the form , where k is a nonzero constant of variation.

Example Suppose that x and y vary directly, and x = 2 when y = 5. Write the function that models the direct variation. Example Suppose that x and y vary inversely, and x = 2 when y = 5. Write the function that models the inverse variation.

Example Suppose that x and y vary inversely, and x = 0. 7 when y = 1. 4. Write the function that models the inverse variation. Example Suppose that x and y vary directly, and x = 0. 7 when y = 1. 4. Write the function that models the direct variation.

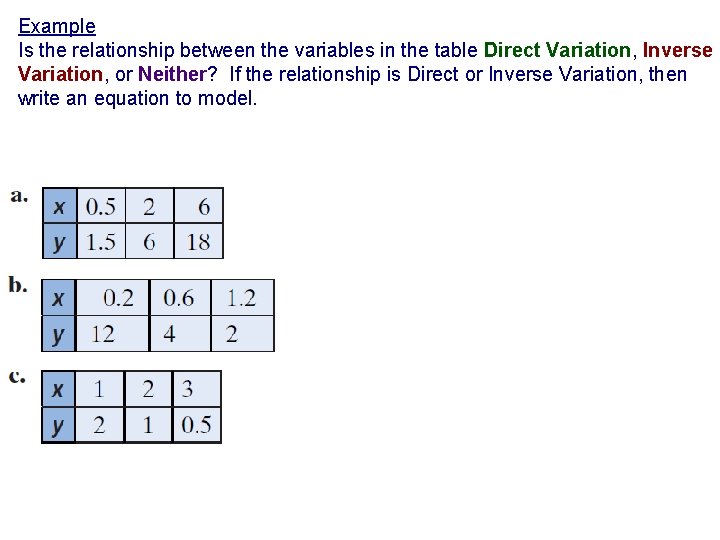
Example Is the relationship between the variables in the table Direct Variation, Inverse Variation, or Neither? If the relationship is Direct or Inverse Variation, then write an equation to model.

Example Is the relationship between the variables in the table Direct Variation, Inverse Variation, or Neither? If the relationship is Direct or Inverse Variation, then write an equation to model.

Example The pressure P of a sample of gas at a constant temperature varies inversely as the volume V. Use the data in the table to write a equation that models the relationship. Use your equation to estimate the pressure when the volume is 11 in 3.

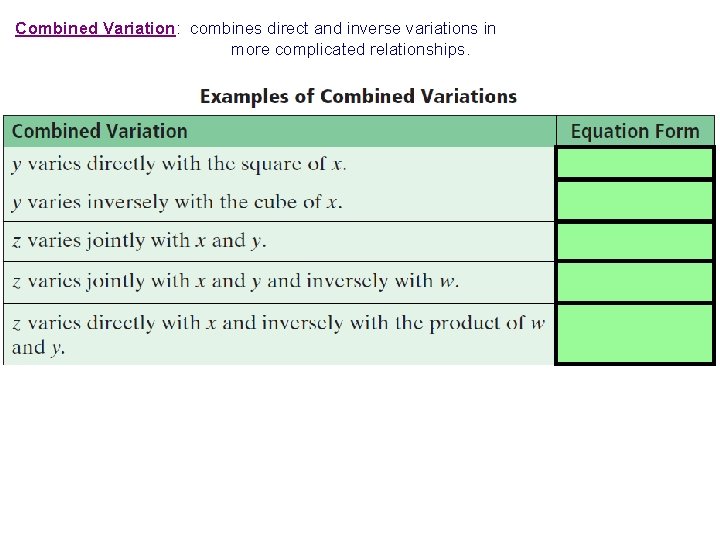
Combined Variation: combines direct and inverse variations in more complicated relationships.

Example:

Example: Suppose z varies directly as x and inversely as the square of y. When x = 35 and y = 7, the value of z is 50. Write a function that models the relationship then find z when x = 5 and y = 10.

End of Day 3 P 412 36 – 45 all P 481 13 – 15, 21 – 27

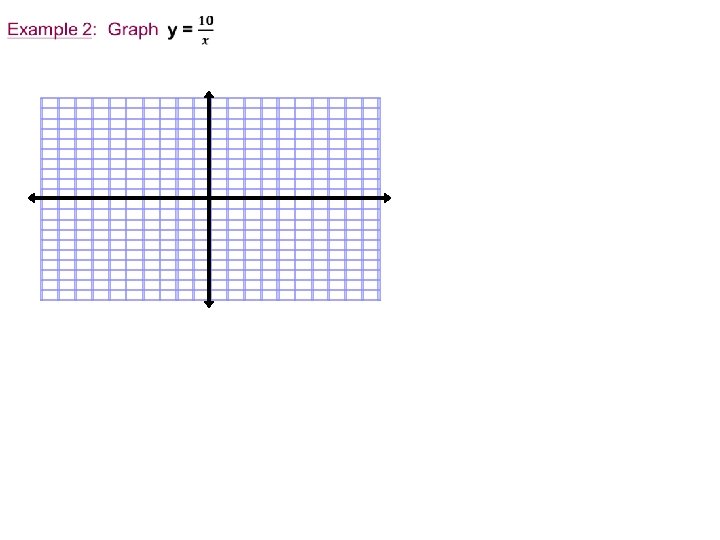
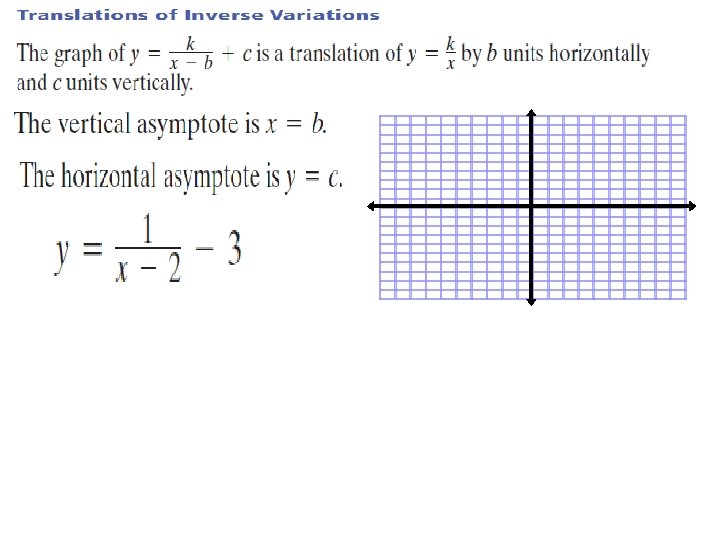
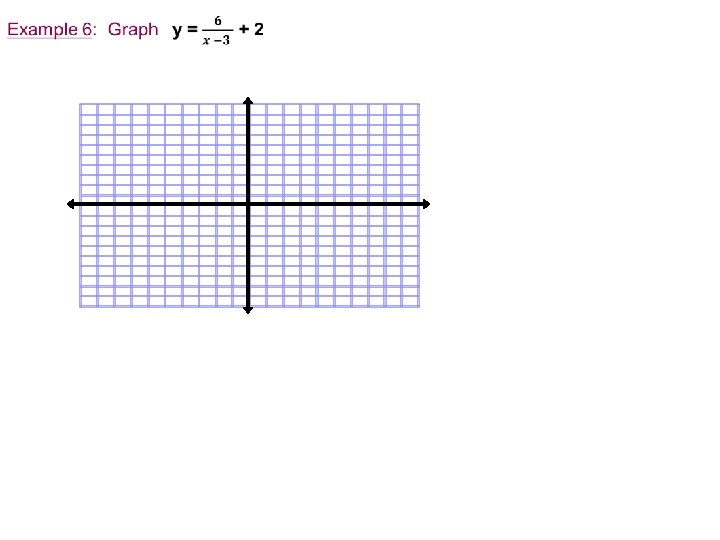
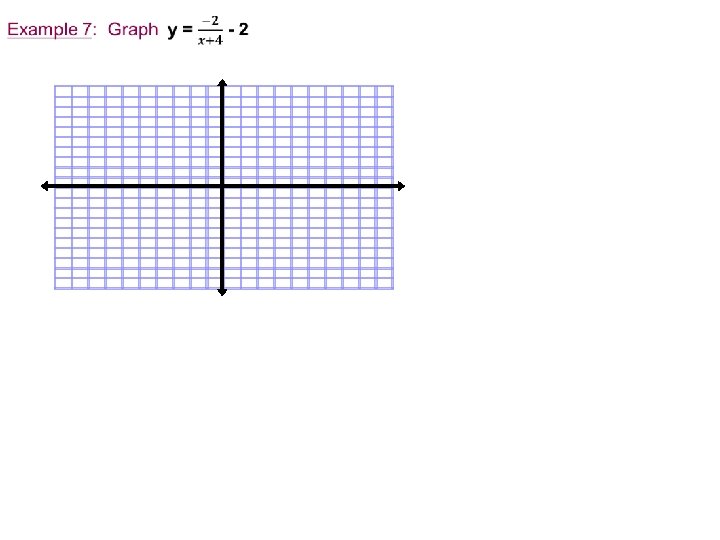
Title: Graphing Inverse Variations Objectives: To learn to graph inverse variations & translations of inverse variation.

Asymptote: line that a graph approaches as x or y increases in value.






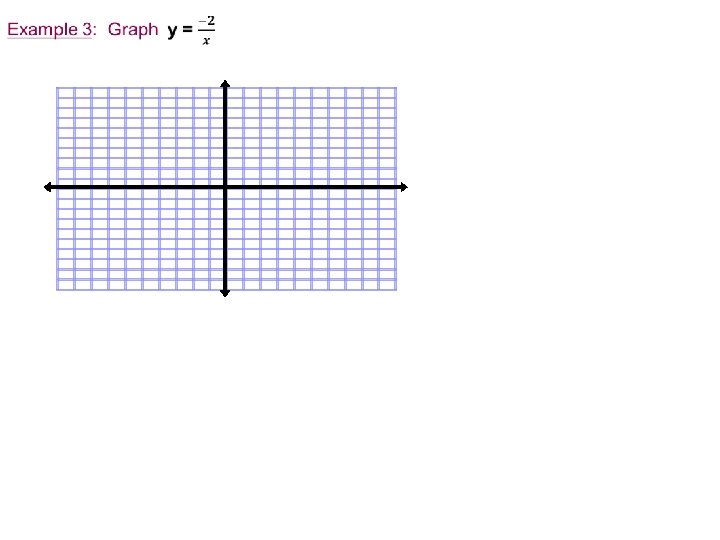
Write an equation for the translation of y = -2/x that has asymptotes at x = 4 and y = -2.

Assignment: In the Algebra 2 Textbook: p. 488 #2, 3, 14 -24

Classwork: Part 1

Classwork: Part 2

Classwork: Part 3 24. 26.

End of Day 5

Unit 6 "Radical and Rational Functions" Title: Rational Expressions Objective: To 1) simplify rational expressions, 2) multiply and divide rational expressions, and 3) identify any restrictions on the variables.

A rational expression is in simplest form when its numerator and denominator have no common factors (other than 1). Simplest Form Not in Simplest Form

Restrictions on a Variable: is any value of a variable that makes the denominator of the original expression or the simplified expression equal zero. Example:

Example:

Example:

Example:

Example:

Example:

End of Day 6

Multiplying and Dividing Rational Expressions Factor all parts of the expression You cancel top to bottom and diagonally When dividing, flip the second fraction and multiply.

Example:

Example:

Example:

Example:

End of Day 7

Unit 6 "Radical and Rational Functions" Title: Adding and Subtracting Rational Expressions Objective: To find the least common multiples of rational expressions and use them to add & subtract rational expressions. Adding/Subtracting Fractions - The denominators must be the same!
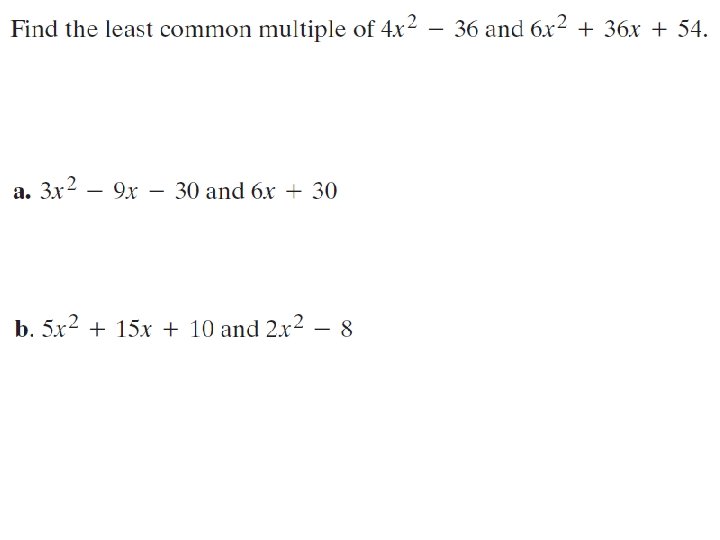
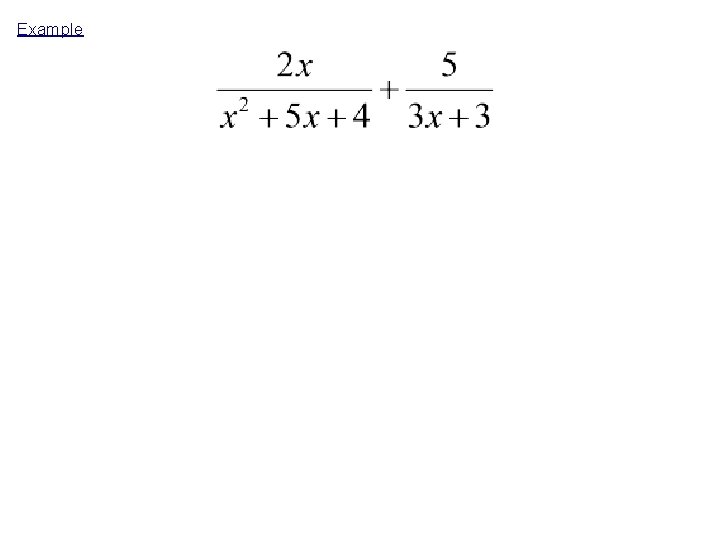
Example
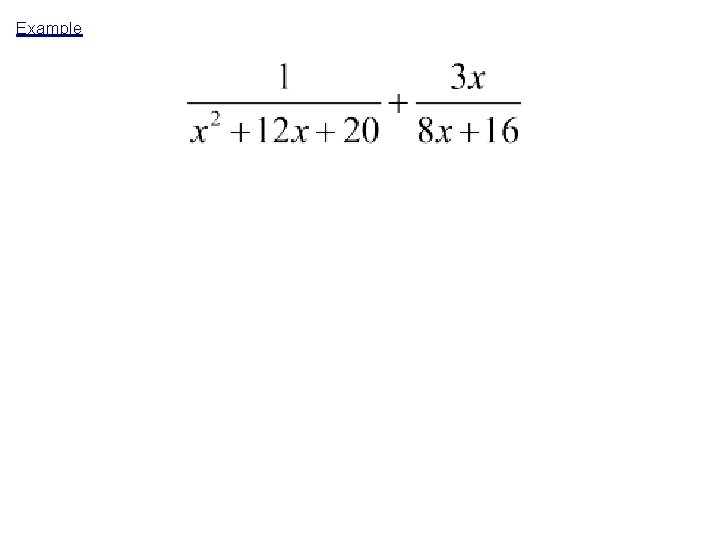
Example

Example
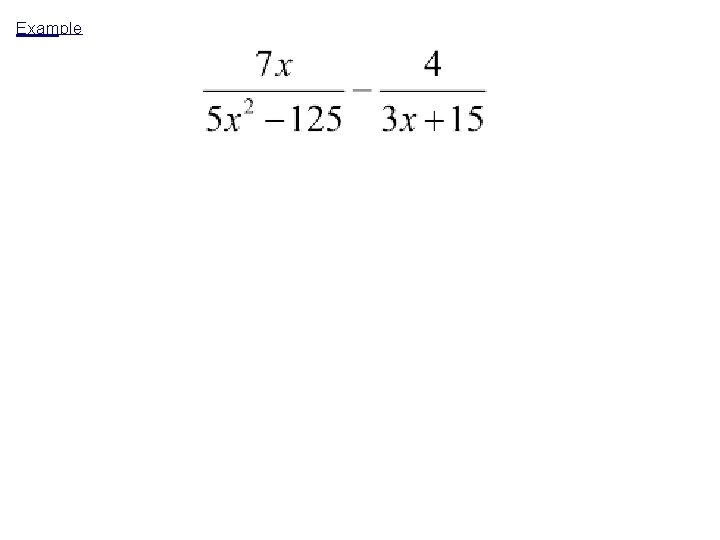
Example

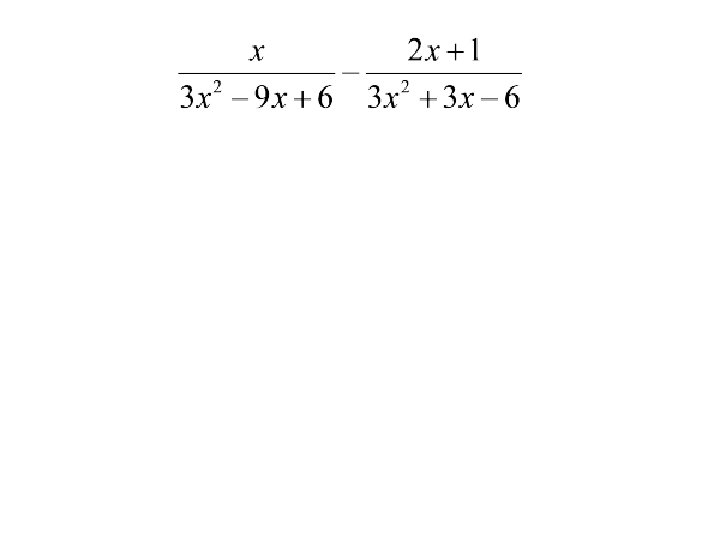

End of Day 8

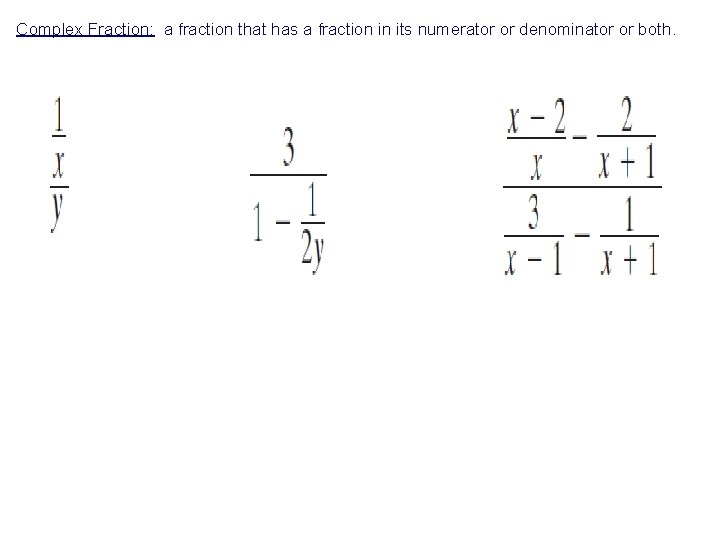
Complex Fractions

Complex Fraction: a fraction that has a fraction in its numerator or denominator or both.
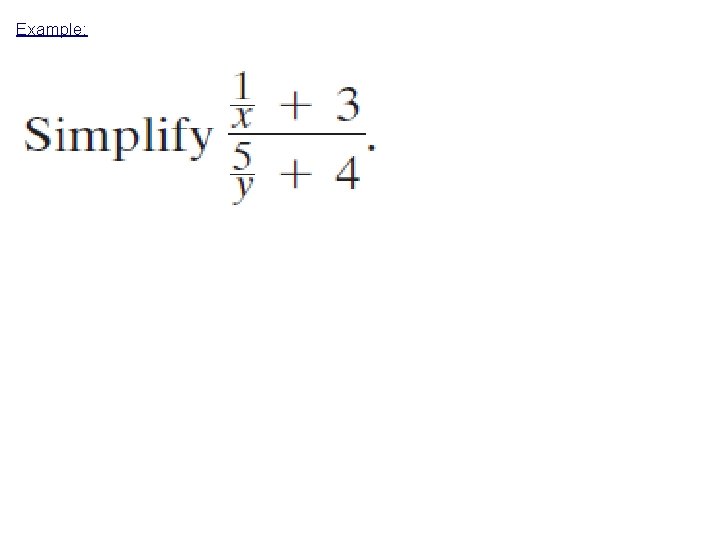
Example:
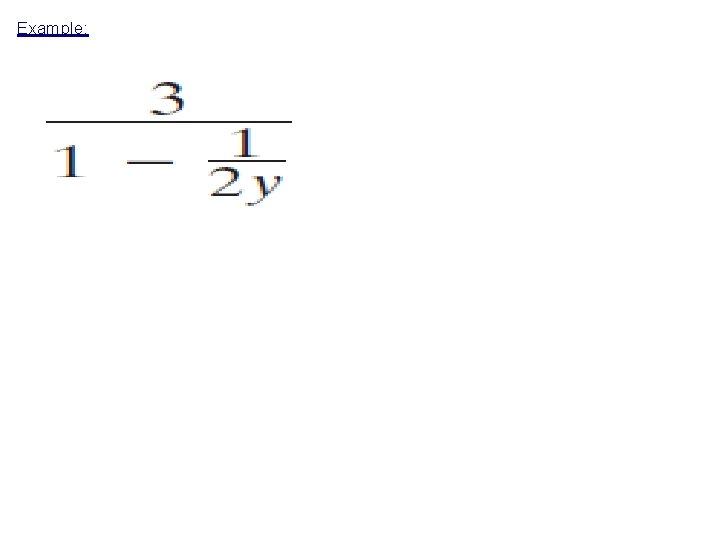
Example:

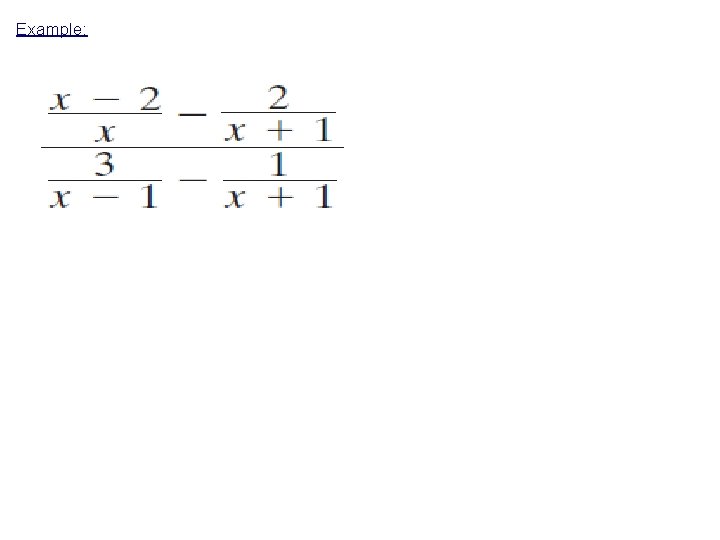
Example:

End of Day

Unit 6 "Radical and Rational Functions" Title: Rational Equations Objective: To solve equations that contain rational expressions and use rational equations in solving problems.

Example Steps: 1. Cross Multiply. 2. Solve equation. 3. Check Answers for Extraneous Solutions!
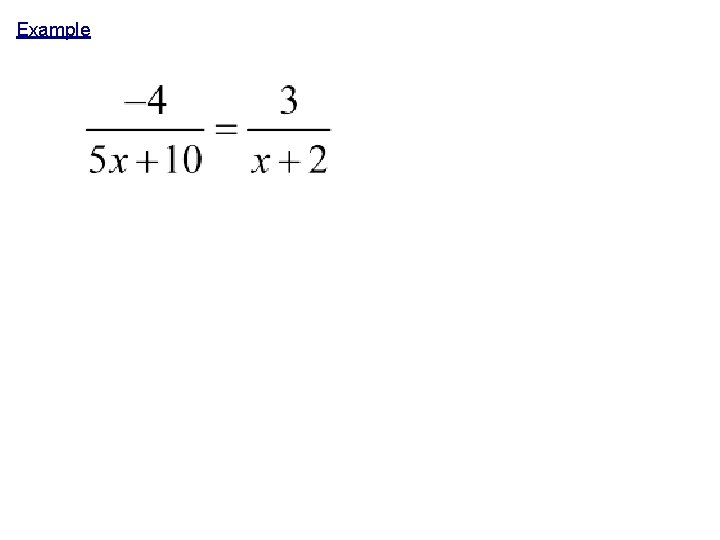
Example
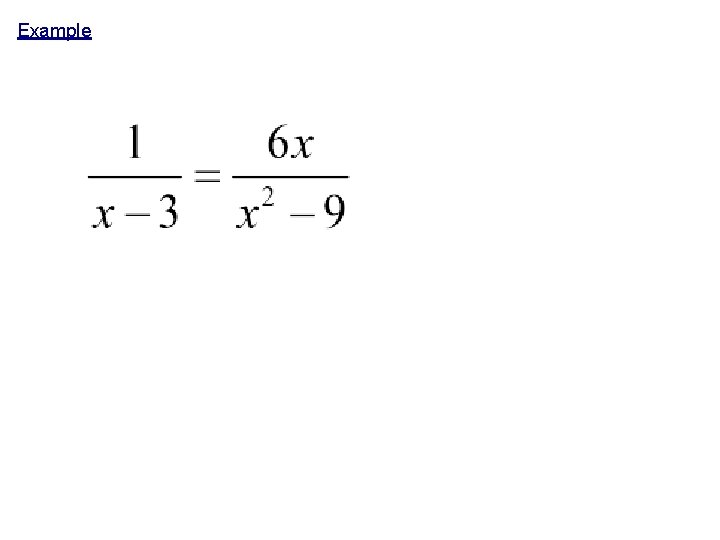
Example
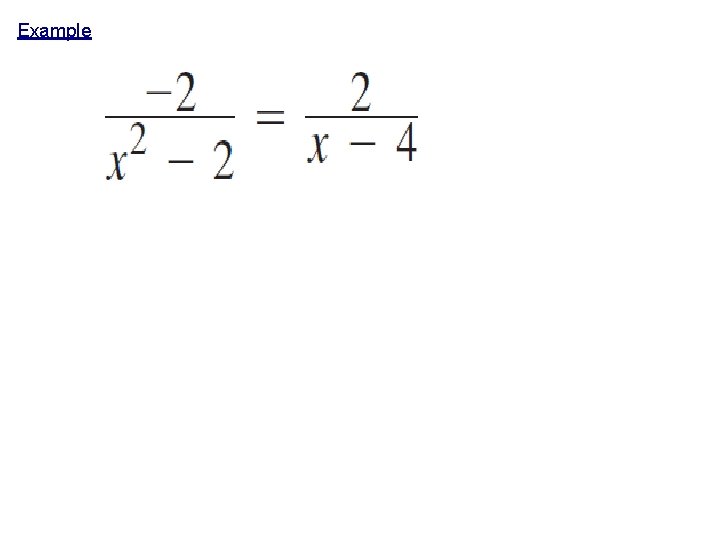
Example

Example Steps: 1. Find the LCD. 2. Multiply each side of equation by the LCD. 3. Solve equation. 4. Check Answers for Extraneous Solutions!
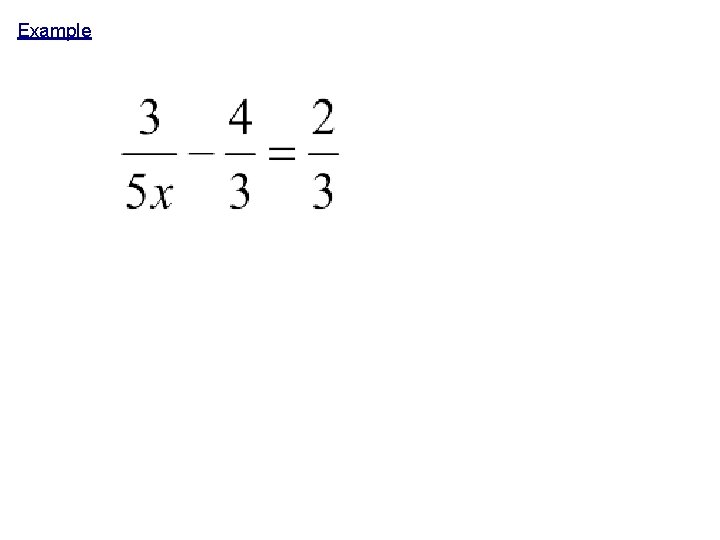
Example
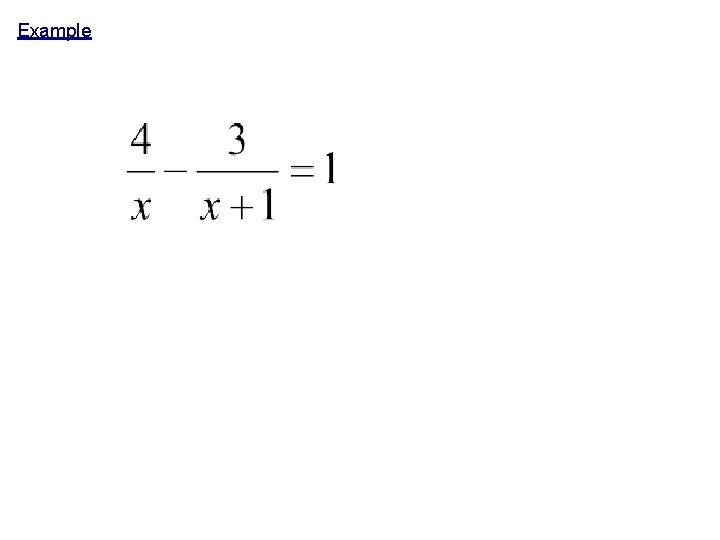
Example
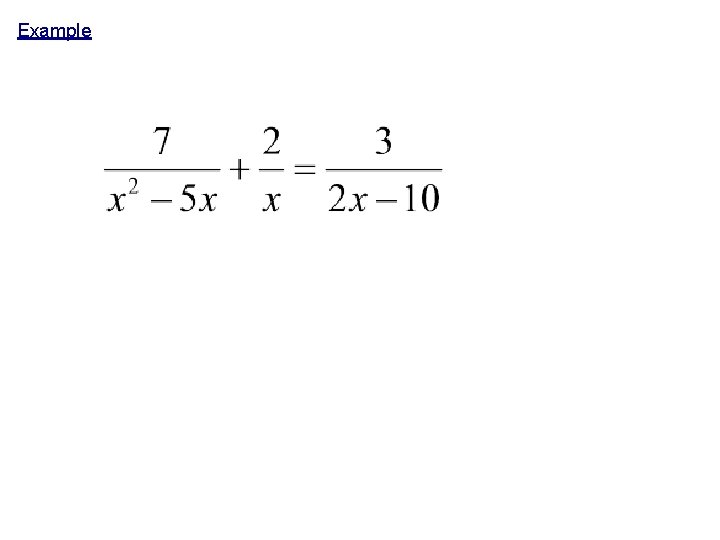
Example
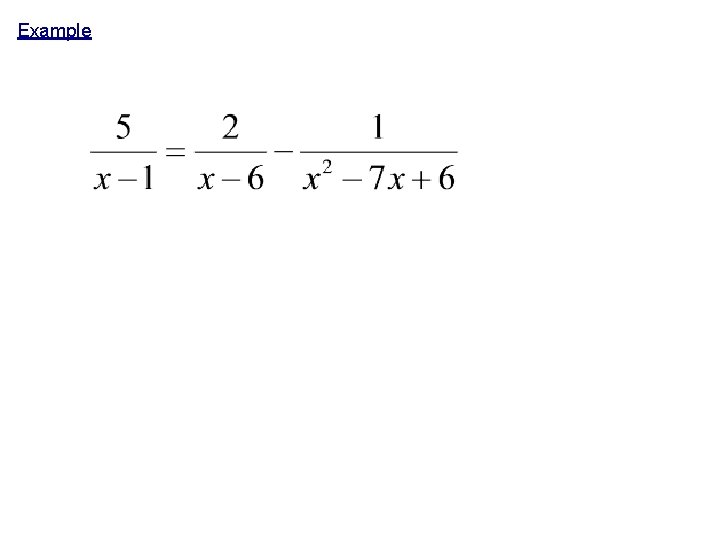
Example
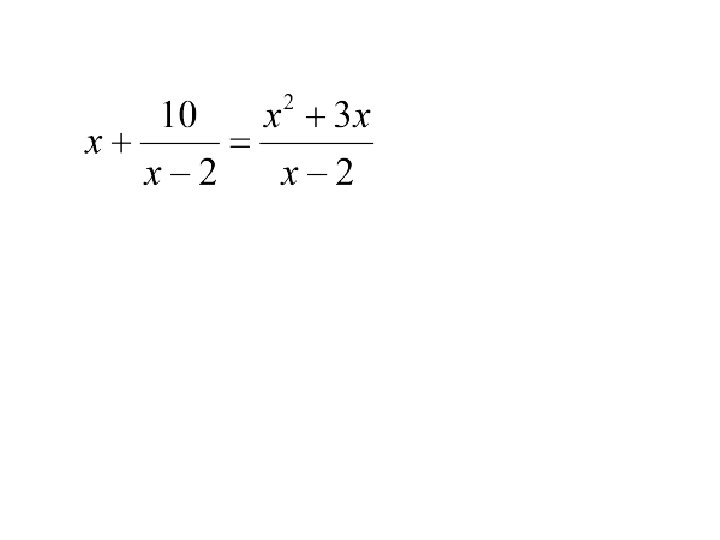


End of Day

Word Problems

Apply Rational Equations One pump can fill a swimming pool with water in 6 hours. A second pump can fill the same pool in 4 hours. If both pumps are used at the same time, how long would it take to fill the pool?

Apply Rational Equations Ben can paint a room in 10 hours. Cody can do it in 8 hours. If they work together, how long would it take to paint the room?

Apply Rational Equations Tim can stuff envelopes three times as fast as his wife Jill. They have to stuff 5000 envelopes for a fund-raiser. Working together, Tim and Jill can complete the job in four hours. How long would it take each of them working alone?

Apply Rational Equations Jim and Alberto have to paint 6000 square feet of hallway in an office building. Alberto works twice as fast Jim. Working together, they can complete the job in 15 hours. How long would it take each of them working alone?

End of Day
 Radical functions and rational exponents unit test
Radical functions and rational exponents unit test Algebra 2 unit 6 radical functions quiz 6-1 answers
Algebra 2 unit 6 radical functions quiz 6-1 answers Unit 6 radical functions homework 1 answer key
Unit 6 radical functions homework 1 answer key Radical functions and rational exponents practice
Radical functions and rational exponents practice Unit 6 radical functions
Unit 6 radical functions Radical functions and rational exponents
Radical functions and rational exponents Lesson 3 existence and uniqueness
Lesson 3 existence and uniqueness Radical functions unit test
Radical functions unit test Root of an equation
Root of an equation Square root 1 to 100
Square root 1 to 100 X 1 2 formula
X 1 2 formula Perfect cube list
Perfect cube list Asymptote rules
Asymptote rules How to write an entire radical
How to write an entire radical What is an entire radical
What is an entire radical Biology roots vanessa jason
Biology roots vanessa jason Economic roots of american imperialism
Economic roots of american imperialism Radical and rational equations
Radical and rational equations 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents Radical and rational expressions
Radical and rational expressions Lesson 11-1 radical expressions and rational exponents
Lesson 11-1 radical expressions and rational exponents Unit 8 rational functions homework 1
Unit 8 rational functions homework 1 Rational exponent to radical form calculator
Rational exponent to radical form calculator Rational zeros therom
Rational zeros therom Possible rational roots
Possible rational roots Solving rational equations and inequalities
Solving rational equations and inequalities Phloem
Phloem Apa itu tuxedo
Apa itu tuxedo Greek and latin roots and affixes unit 1 answer key
Greek and latin roots and affixes unit 1 answer key 5-7 practice b radical functions answers
5-7 practice b radical functions answers Radical functions in real life
Radical functions in real life Functions of roots
Functions of roots Propagative roots functions
Propagative roots functions Root structure
Root structure Unit 8 greek and latin roots
Unit 8 greek and latin roots Fort latin root
Fort latin root Refuge sentence in english
Refuge sentence in english Erg greek root
Erg greek root Graph greek root
Graph greek root Greek root vis
Greek root vis Pel/puls
Pel/puls Words with the root sta
Words with the root sta When they reached the opulent port the sailors saw
When they reached the opulent port the sailors saw Vocabulary from latin and greek roots unit 7
Vocabulary from latin and greek roots unit 7 Unit 1 the real numbers homework 6 square and cube roots
Unit 1 the real numbers homework 6 square and cube roots Vertical asymptote
Vertical asymptote Rational expressions and functions
Rational expressions and functions Irrational function definition
Irrational function definition Rational functions holes and asymptotes
Rational functions holes and asymptotes Vertical answer
Vertical answer Chapter 4 polynomial and rational functions
Chapter 4 polynomial and rational functions Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Sketch the graph of the following rational function
Sketch the graph of the following rational function Graphs and properties of rational functions
Graphs and properties of rational functions Horizontal asymptote
Horizontal asymptote Lesson 3: rational functions and their graphs
Lesson 3: rational functions and their graphs Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Unit 10, unit 10 review tests, unit 10 general test
Unit 10, unit 10 review tests, unit 10 general test Rational functions parent function
Rational functions parent function Rational function transformation
Rational function transformation Properties of rational function
Properties of rational function Limits of rational functions
Limits of rational functions Rational fraction
Rational fraction Rational function examples
Rational function examples What are rational functions
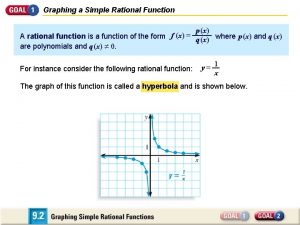
What are rational functions Graphing simple rational functions
Graphing simple rational functions Gina wilson 2012
Gina wilson 2012 End behavior of rational functions
End behavior of rational functions Asymptote rules
Asymptote rules State the excluded values for each rational expression
State the excluded values for each rational expression Analyzing rational functions
Analyzing rational functions Rational function in real life
Rational function in real life Algebra 2b unit 3 trigonometry
Algebra 2b unit 3 trigonometry Short run behavior
Short run behavior Graphing rational functions quiz
Graphing rational functions quiz Graphing rational functions
Graphing rational functions Synthetic division steps
Synthetic division steps What is the sum of a rational and irrational number
What is the sum of a rational and irrational number Rational equations
Rational equations Inverse of a rational function
Inverse of a rational function Rational graph
Rational graph 2-5 rational functions
2-5 rational functions Ib math sl rational functions questions
Ib math sl rational functions questions What is a rational function
What is a rational function Simplifying rational functions
Simplifying rational functions Rational graph
Rational graph Graph rational functions
Graph rational functions Ratey rational functions
Ratey rational functions Rational function summary
Rational function summary Rational functions
Rational functions Rational numbers
Rational numbers Function evaluator
Function evaluator Irrational numbers
Irrational numbers Rational functions grapher
Rational functions grapher Asymptote examples
Asymptote examples Domain and range of rational function
Domain and range of rational function I can evaluate functions
I can evaluate functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Absolute value piecewise function
Absolute value piecewise function Unit 8 review logarithms
Unit 8 review logarithms Unit 5 exponential and logarithmic functions answers
Unit 5 exponential and logarithmic functions answers Formalizing relations and functions
Formalizing relations and functions Polynomial function table
Polynomial function table 4-6 formalizing relations and functions
4-6 formalizing relations and functions Unit circle radians
Unit circle radians Ante root word examples
Ante root word examples Roots and tubers should be stored dry and unpeeled
Roots and tubers should be stored dry and unpeeled Root word dyna
Root word dyna Inequalities
Inequalities Solving radical inequalities
Solving radical inequalities Lesson 7 - graphing radical equations and inequalities
Lesson 7 - graphing radical equations and inequalities Solving radical equations and inequalities
Solving radical equations and inequalities Root equation
Root equation 11-4 multiplying and dividing rational expressions
11-4 multiplying and dividing rational expressions Adding subtracting and multiplying radical expressions
Adding subtracting and multiplying radical expressions Reconstruction venn diagram
Reconstruction venn diagram Solving square root and other radical equations
Solving square root and other radical equations