8 7 Radical Functions Objectives Graph radical functions

8 -7 Radical Functions Objectives Graph radical functions and inequalities. Transform radical functions by changing parameters. Holt Algebra 2

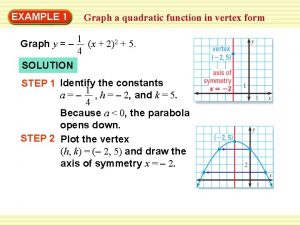
8 -7 Radical Functions Recall that exponential and logarithmic functions are inverse functions. Quadratic and cubic functions have inverses as well. The graphs below show the inverses of the quadratic parent function and cubic parent function. Holt Algebra 2

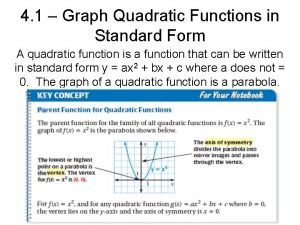
8 -7 Radical Functions Notice that the inverses of f(x) = x 2 is not a function because it fails the vertical line test. However, if we limit the domain of f(x) = x 2 to x ≥ 0, its inverse is the function. A radical function is a function whose rule is a radical expression. A square-root function is a radical function involving. The square-root parent function is. The cube-root parent function is. Holt Algebra 2

8 -7 Radical Functions Example 1 A: Graphing Radical Functions Graph each function and identify its domain and range. Make a table of values. Plot enough ordered pairs to see the shape of the curve. Because the square root of a negative number is imaginary, choose only nonnegative values for x – 3. Holt Algebra 2

8 -7 Radical Functions Example 1 A Continued x (x, f(x)) 3 (3, 0) 4 7 12 (4, 1) (7, 2) (12, 3) ● ● The domain is {x|x ≥ 3}, and the range is {y|y ≥ 0}. Holt Algebra 2

8 -7 Radical Functions Example 1 B: Graphing Radical Functions Graph each function and identify its domain and range. Make a table of values. Plot enough ordered pairs to see the shape of the curve. Choose both negative and positive values for x. Holt Algebra 2

8 -7 Radical Functions Example 1 B Continued x (x, f(x)) – 6 (– 6, – 4) 1 (1, – 2) 2 (2, 0) 3 (3, 2) 10 (10, 4) ● ● ● The domain is the set of all real numbers. The range is also the set of all real numbers Holt Algebra 2

8 -7 Radical Functions Example 1 B Continued Check Graph the function on a graphing calculator. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 1 a Graph each function and identify its domain and range. Make a table of values. Plot enough ordered pairs to see the shape of the curve. Choose both negative and positive values for x. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 1 a Continued x (x, f(x)) – 8 (– 8, – 2) – 1 (– 1, – 1) 0 (0, 0) 1 (1, 1) 8 (8, 2) • • • The domain is the set of all real numbers. The range is also the set of all real numbers. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 1 a Continued Check Graph the function on a graphing calculator. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 1 b Graph each function, and identify its domain and range. x (x, f(x)) – 1 (– 1, 0) 3 8 15 (3, 2) (8, 3) (15, 4) • • The domain is {x|x ≥ – 1}, and the range is {y|y ≥ 0}. Holt Algebra 2

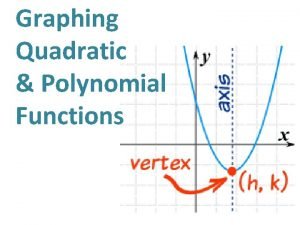
8 -7 Radical Functions The graphs of radical functions can be transformed by using methods similar to those used to transform linear, quadratic, polynomial, and exponential functions. This lesson will focus on transformations of square-root functions. Holt Algebra 2

8 -7 Radical Functions Holt Algebra 2
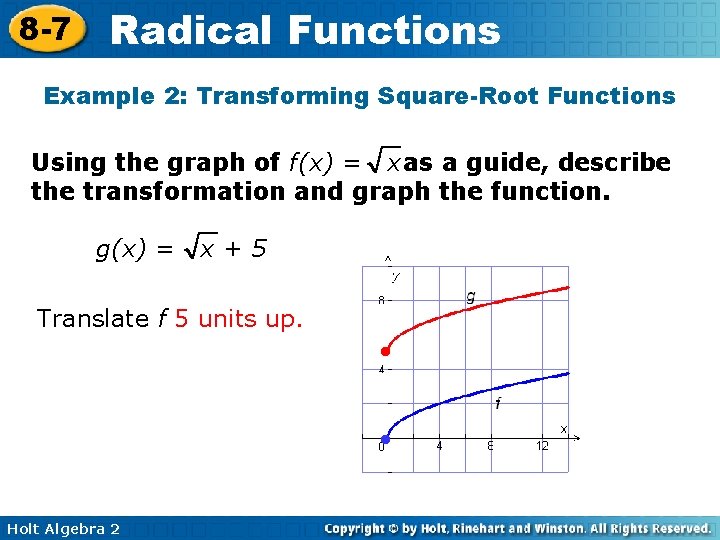
8 -7 Radical Functions Example 2: Transforming Square-Root Functions Using the graph of f(x) = x as a guide, describe the transformation and graph the function. g(x) = x+5 Translate f 5 units up. • • Holt Algebra 2
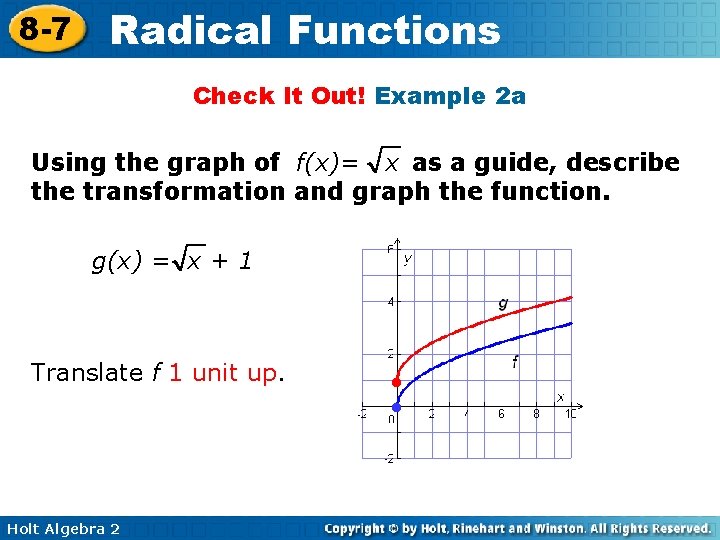
8 -7 Radical Functions Check It Out! Example 2 a Using the graph of f(x)= x as a guide, describe the transformation and graph the function. g(x) = x + 1 Translate f 1 unit up. Holt Algebra 2 • •
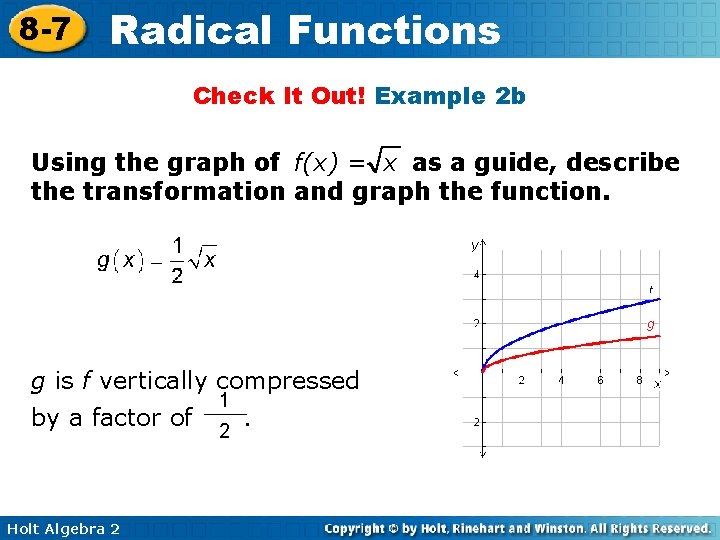
8 -7 Radical Functions Check It Out! Example 2 b Using the graph of f(x) = x as a guide, describe the transformation and graph the function. g is f vertically compressed by a factor of Holt Algebra 2 1 2 .

8 -7 Radical Functions Transformations of square-root functions are summarized below. Holt Algebra 2
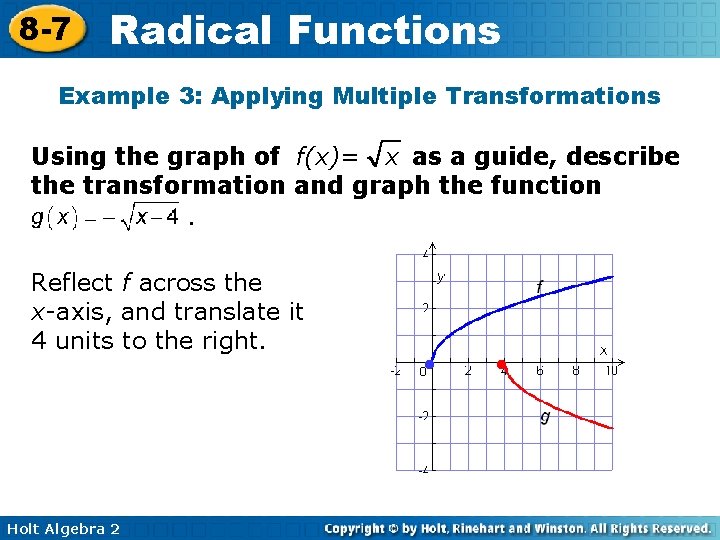
8 -7 Radical Functions Example 3: Applying Multiple Transformations Using the graph of f(x)= x as a guide, describe the transformation and graph the function. Reflect f across the x-axis, and translate it 4 units to the right. Holt Algebra 2 • •
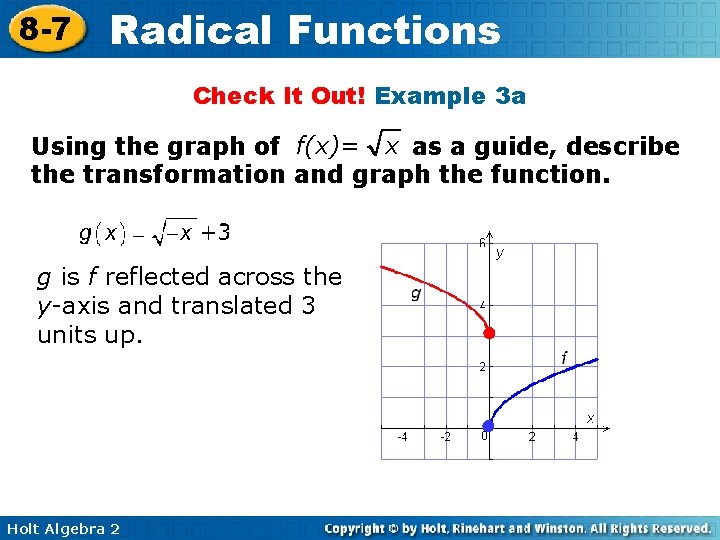
8 -7 Radical Functions Check It Out! Example 3 a Using the graph of f(x)= x as a guide, describe the transformation and graph the function. g is f reflected across the y-axis and translated 3 units up. ● ● Holt Algebra 2
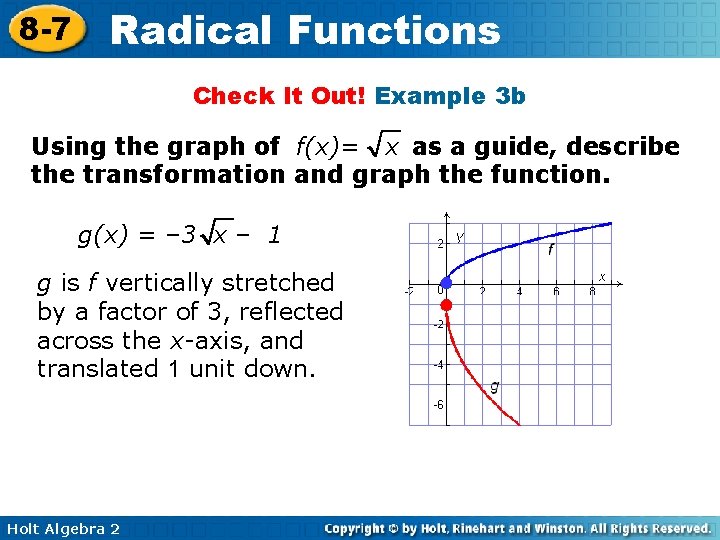
8 -7 Radical Functions Check It Out! Example 3 b Using the graph of f(x)= x as a guide, describe the transformation and graph the function. g(x) = – 3 x – 1 g is f vertically stretched by a factor of 3, reflected across the x-axis, and translated 1 unit down. Holt Algebra 2 ● ●

8 -7 Radical Functions Example 4: Writing Transformed Square-Root Functions Use the description to write the square-root function g. The parent function f(x)= x is reflected across the x-axis, compressed vertically by a factor of 1 5 , and translated down 5 units. Step 1 Identify how each transformation affects the function. Reflection across the x-axis: a is negative Vertical compression by a factor of Translation 5 units down: k = – 5 Holt Algebra 2 1 5 a=– 1 5

8 -7 Radical Functions Example 4 Continued Step 2 Write the transformed function. æ 1ö g(x) = ç - ÷ x + (- 5) Substitute – 1 for a and – 5 for k. 5 è 5ø Simplify. Holt Algebra 2
8 -7 Radical Functions Example 4 Continued Check Holt Algebra 2 Graph both functions on a graphing calculator. The g indicates the given transformations of f.

8 -7 Radical Functions Check It Out! Example 4 Use the description to write the square-root function g. The parent function f(x)= x is reflected across the x-axis, stretched vertically by a factor of 2, and translated 1 unit up. Step 1 Identify how each transformation affects the function. Reflection across the x-axis: a is negative Vertical compression by a factor of 2 Translation 5 units down: k = 1 Holt Algebra 2 a = – 2

8 -7 Radical Functions Check It Out! Example 4 Continued Step 2 Write the transformed function. Substitute – 2 for a and 1 for k. Simplify. Check Graph both functions on a graphing calculator. The g indicates the given transformations of f. Holt Algebra 2

8 -7 Radical Functions Example 5: Business Application A framing store uses the function to determine the cost c in dollars of glass for a picture with an area a in square inches. The store charges an addition $6. 00 in labor to install the glass. Write the function d for the total cost of a piece of glass, including installation, and use it to estimate the total cost of glass for a picture with an area of 192 in 2. Holt Algebra 2

8 -7 Radical Functions Example 5 Continued Step 1 To increase c by 6. 00, add 6 to c. Step 2 Find a value of d for a picture with an area of 192 in 2. Substitute 192 for a and simplify. The cost for the glass of a picture with an area of 192 in 2 is about $13. 13 including installation. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 5 Special airbags are used to protect scientific equipment when a rover lands on the surface of 64 x Mars. On Earth, the function f(x) = approximates an object’s downward velocity in feet per second as the object hits the ground after bouncing x ft in height. The downward velocity function for the Moon is a horizontal stretch of f by a factor of about 25 4 Write the velocity function h for the Moon, and use it to estimate the downward velocity of a landing craft at the end of a bounce 50 ft in height. Holt Algebra 2 .

8 -7 Radical Functions Check It Out! Example 5 Continued Step 1 To compress f horizontally by a factor of 4 multiply f by. 25 , 4 25 h (x ) = æ 4 ö f ç x ÷= è 25 ø 4 256 · 64 x = 25 25 Step 2 Find the value of g for a bounce of 50 ft. 256 h (x ) = · 50 » 23 25 Substitute 50 for x and simplify. The landing craft will hit the Moon’s surface with a downward velocity of about 23 ft at the end of the bounce. Holt Algebra 2

8 -7 Radical Functions In addition to graphing radical functions, you can also graph radical inequalities. Use the same procedure you used for graphing linear and quadratic inequalities. Holt Algebra 2

8 -7 Radical Functions Example 6: Graphing Radical Inequalities Graph the inequality . Step 1 Use the related equation y =2 x -3 to make a table of values. x y Holt Algebra 2 0 – 3 1 – 1 4 1 9 3

8 -7 Radical Functions Example 6 Continued Step 2 Use the table to graph the boundary curve. The inequality sign is >, so use a dashed curve and shade the area above it. Because the value of x cannot be negative, do not shade left of the yaxis. Holt Algebra 2

8 -7 Radical Functions Example 6 Continued Check Choose a point in the solution region, such as (1, 0), and test it in the inequality. 0 > 2(1) – 3 0 > – 1 Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 6 a Graph the inequality. Step 1 Use the related equation y = make a table of values. x y Holt Algebra 2 – 4 0 – 3 1 0 2 5 3 x+4 to

8 -7 Radical Functions Check It Out! Example 6 a Continued Step 2 Use the table to graph the boundary curve. The inequality sign is >, so use a dashed curve and shade the area above it. Because the value of x cannot be less than – 4, do not shade left of – 4. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 6 a Continued Check Choose a point in the solution region, such as (0, 4), and test it in the inequality. 4 > (0) + 4 4>2 Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 6 b Graph the inequality. Step 1 Use the related equation y = make a table of values. x y Holt Algebra 2 – 4 0 – 3 1 0 2 5 3 3 x - 3 to
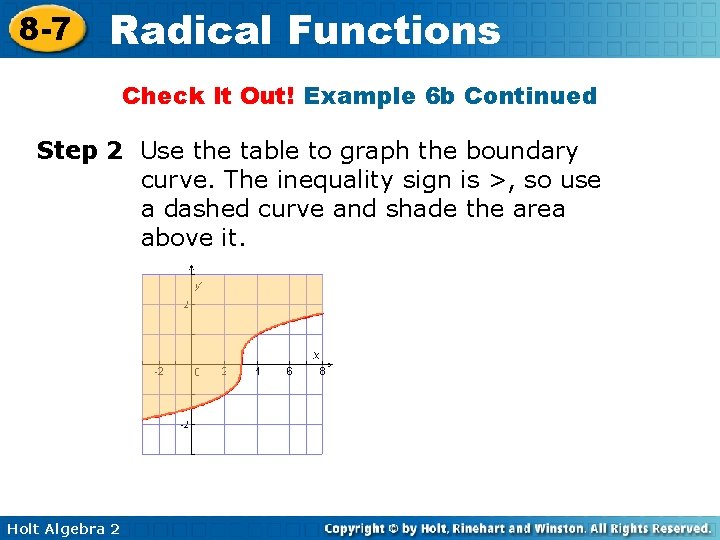
8 -7 Radical Functions Check It Out! Example 6 b Continued Step 2 Use the table to graph the boundary curve. The inequality sign is >, so use a dashed curve and shade the area above it. Holt Algebra 2

8 -7 Radical Functions Check It Out! Example 6 b Continued Check Choose a point in the solution region, such as (4, 2), and test it in the inequality. 2≥ 1 Holt Algebra 2

8 -7 Radical Functions Lesson Quiz: Part I 1. Graph the function range and domain. and identify its D: {x|x≥ – 4}; R: {y|y≥ 0} • Holt Algebra 2
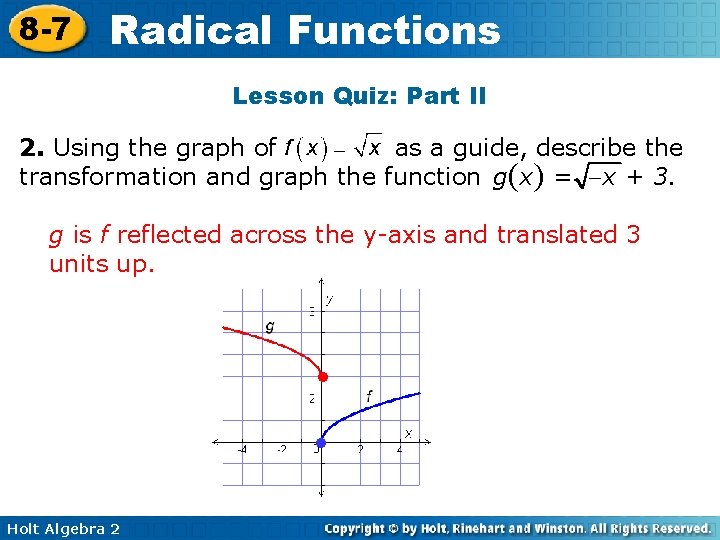
8 -7 Radical Functions Lesson Quiz: Part II 2. Using the graph of as a guide, describe the transformation and graph the function g(x) = -x + 3. g is f reflected across the y-axis and translated 3 units up. • • Holt Algebra 2
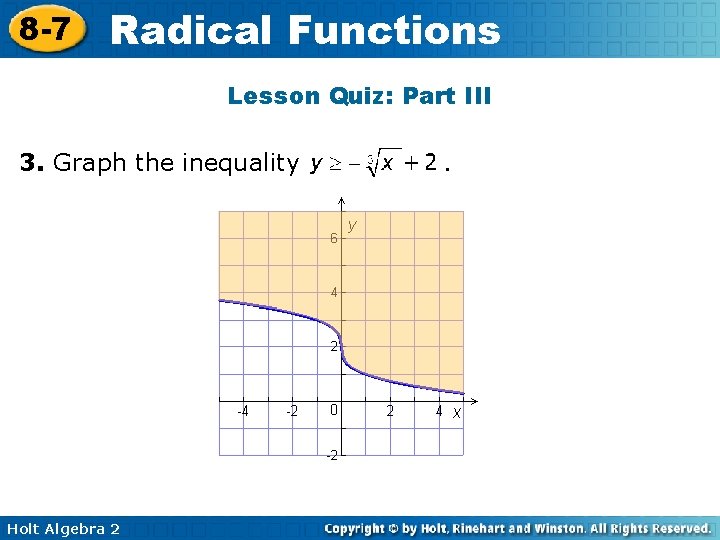
8 -7 Radical Functions Lesson Quiz: Part III 3. Graph the inequality Holt Algebra 2 .
- Slides: 43