Solving Radical Equations 8 8 and Inequalities Warm















































- Slides: 49

Solving Radical Equations 8 -8 and Inequalities Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

8 -8 Solving Radical Equations and Inequalities Warm Up Simplify each expression. Assume all variables are positive. 1. 2. 3. 4. Write each expression in radical form. 5. 6. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Objective Solve radical equations and inequalities. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Vocabulary radical equation radical inequality Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities A radical equation contains a variable within a radical. Recall that you can solve quadratic equations by taking the square root of both sides. Similarly, radical equations can be solved by raising both sides to a power. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Remember! For a square root, the index of the radical is 2. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 1 A: Solving Equations Containing One Radical Solve each equation. Check Subtract 5. Simplify. Square both sides. Simplify. Solve for x. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 1 B: Solving Equations Containing One Radical Solve each equation. Check 7 3 5 x - 7 84 = 7 7 Divide by 7. 7 Simplify. Cube both sides. Simplify. Solve for x. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 1 a Solve the equation. Check Subtract 4. Simplify. Square both sides. Simplify. Solve for x. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 1 b Solve the equation. Check Cube both sides. Simplify. Solve for x. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 1 c Solve the equation. Check Divide by 6. Square both sides. Simplify. Solve for x. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 2: Solving Equations Containing Two Radicals Solve Square both sides. 7 x + 2 = 9(3 x – 2) Simplify. 7 x + 2 = 27 x – 18 Distribute. 20 = 20 x 1=x Holt Algebra 2 Solve for x.

8 -8 Solving Radical Equations and Inequalities Example 2 Continued Check 3 Holt Algebra 2 3

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 2 a Solve each equation. Square both sides. 8 x + 6 = 9 x 6=x Simplify. Solve for x. Check Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 2 b Solve each equation. Cube both sides. x + 6 = 8(x – 1) Simplify. x + 6 = 8 x – 8 14 = 7 x 2 =x Distribute. Solve for x. Check 2 Holt Algebra 2 2

8 -8 Solving Radical Equations and Inequalities Raising each side of an equation to an even power may introduce extraneous solutions. Helpful Hint You can use the intersect feature on a graphing calculator to find the point where the two curves intersect. Holt Algebra 2

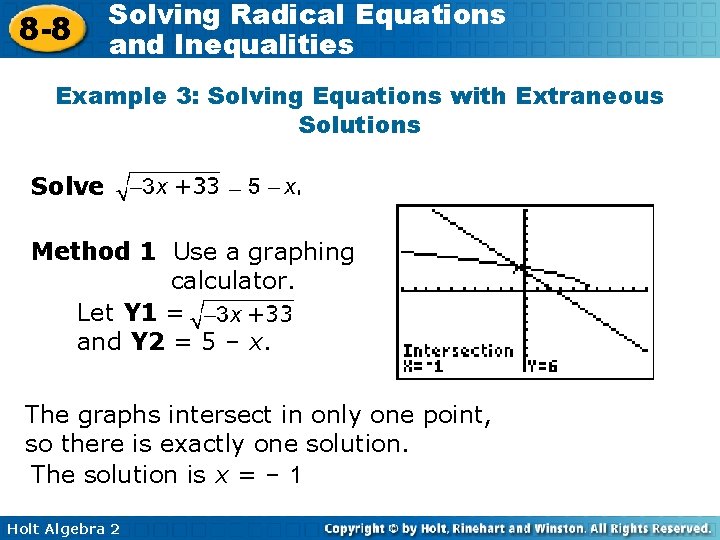
8 -8 Solving Radical Equations and Inequalities Example 3: Solving Equations with Extraneous Solutions Solve . Method 1 Use a graphing calculator. Let Y 1 = and Y 2 = 5 – x. The graphs intersect in only one point, so there is exactly one solution. The solution is x = – 1 Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 3 Continued Method 2 Use algebra to solve the equation. Step 1 Solve for x. Square both sides. – 3 x + 33 = 25 – 10 x + x 2 0 = x 2 – 7 x – 8 0 = (x – 8)(x + 1) x – 8 = 0 or x + 1 = 0 x = 8 or x = – 1 Holt Algebra 2 Simplify. Write in standard form. Factor. Solve for x.

8 -8 Solving Radical Equations and Inequalities Example 3 Continued Method 2 Use algebra to solve the equation. Step 2 Use substitution to check for extraneous solutions. 3 – 3 x 6 6 Because x = 8 is extraneous, the only solution is x = – 1. Holt Algebra 2

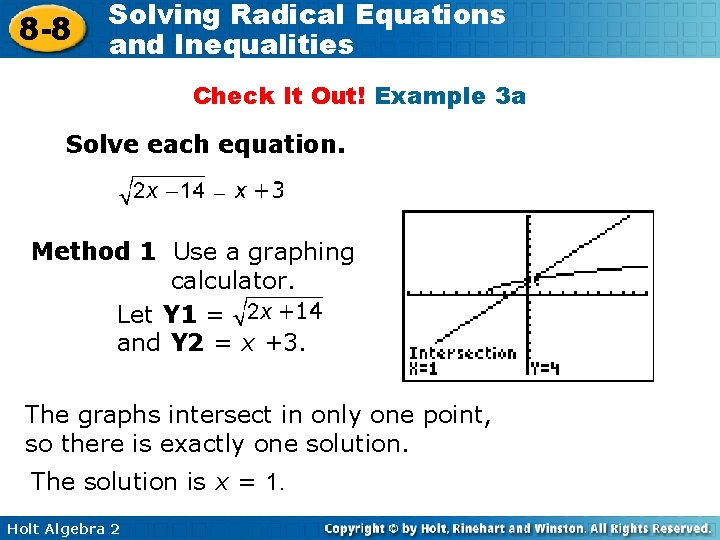
8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 a Solve each equation. Method 1 Use a graphing calculator. Let Y 1 = and Y 2 = x +3. The graphs intersect in only one point, so there is exactly one solution. The solution is x = 1. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 a Continued Method 2 Use algebra to solve the equation. Step 1 Solve for x. Square both sides. 2 x + 14 = x 2 + 6 x + 9 0 = x 2 + 4 x – 5 0 = (x + 5)(x – 1) x + 5 = 0 or x – 1 = 0 x = – 5 or x = 1 Holt Algebra 2 Simplify. Write in standard form. Factor. Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 a Continued Method 1 Use algebra to solve the equation. Step 2 Use substitution to check for extraneous solutions. 2 – 2 x 4 4 Because x = – 5 is extraneous, the only solution is x = 1. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 b Solve each equation. Method 1 Use a graphing calculator. Let Y 1 = and Y 2 = –x +4. The graphs intersect in two points, so there are two solutions. The solutions are x = – 4 and x = 3. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 b Continued Method 2 Use algebra to solve the equation. Step 1 Solve for x. Square both sides. – 9 x + 28 = x 2 – 8 x + 16 0 = x 2 + x – 12 0 = (x + 4)(x – 3) x + 4 = 0 or x – 3 = 0 x = – 4 or x = 3 Holt Algebra 2 Simplify. Write in standard form. Factor. Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 3 b Continued Method 1 Use algebra to solve the equation. Step 2 Use substitution to check for extraneous solutions. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Remember! To find a power, multiply the exponents. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 4 A: Solving Equations with Rational Exponents Solve each equation. (5 x + 7) 1 3 =3 Write in radical form. Cube both sides. 5 x + 7 = 27 5 x = 20 x= 4 Holt Algebra 2 Simplify. Factor. Solve for x.

8 -8 Solving Radical Equations and Inequalities Example 4 B: Solving Equations with Rational Exponents 2 x = (4 x + 8) 1 2 Step 1 Solve for x. 1 2 (2 x)2 = [(4 x + 8) ]2 Raise both sides to the reciprocal power. 4 x 2 = 4 x + 8 Simplify. 4 x 2 – 4 x – 8 = 0 Write in standard form. 4(x 2 – x – 2) = 0 Factor out the GCF, 4. 4(x – 2)(x + 1) = 0 Factor. 4 ≠ 0, x – 2 = 0 or x + 1 = 0 Solve for x. x = 2 or x = – 1 Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 4 B Continued Step 2 Use substitution to check for extraneous solutions. 2 x = (4 x + 8) 1 2 2(2) (4(2) + 8) 4 4 2 x = (4 x + 8) 1 2 16 4 The only solution is x = 2. Holt Algebra 2 1 2 2(– 1) (4(– 1) + 8) – 2 1 2 4 2 x 1 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 4 a Solve each equation. (x + 5) 1 3 =3 Write in radical form. Cube both sides. x + 5 = 27 x = 22 Holt Algebra 2 Simplify. Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 4 b (2 x + 15) 1 2 =x Step 1 Solve for x. 1 2 2 [(2 x + 15) ] = (x) 2 2 x + 15 = x 2 – 2 x – 15 = 0 (x – 5)(x + 3) = 0 x – 5 = 0 or x + 3 = 0 x = 5 or x = – 3 Holt Algebra 2 Raise both sides to the reciprocal power. Simplify. Write in standard form. Factor. Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 4 b Continued Step 2 Use substitution to check for extraneous solutions. (2 x + 15) 1 2 (2(5) + 15) (10 + 15) 5 1 2 =x 5 5 5 The only solution is x = 5. Holt Algebra 2 (2 x + 15) 1 2 (2(– 3) + 15) (– 6 + 15) 3 =x 1 2 – 3 – 3 x

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 4 c 1 2 3(x + 6) = 9 1 2 2 [3(x + 6) ] = (9) Raise both sides to the reciprocal power. 9(x + 6) = 81 Simplify. 9 x + 54 = 81 Distribute 9. 9 x = 27 x=3 Holt Algebra 2 2 Simplify. Solve for x.

8 -8 Solving Radical Equations and Inequalities A radical inequality is an inequality that contains a variable within a radical. You can solve radical inequalities by graphing or using algebra. Remember! A radical expression with an even index and a negative radicand has no real roots. Holt Algebra 2

Solving Radical Equations and Inequalities 8 -8 Example 5: Solving Radical Inequalities Solve . Method 1 Use a graph and a table. On a graphing calculator, let Y 1 = and Y 2 = 9. The graph of Y 1 is at or below the graph of Y 2 for values of x between 3 and 21. Notice that Y 1 is undefined when < 3. The solution is 3 ≤ x ≤ 21. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 5 Continued Method 2 Use algebra to solve the inequality. Step 1 Solve for x. Subtract 3. Square both sides. Simplify. 2 x ≤ 42 x ≤ 21 Holt Algebra 2 Solve for x.

8 -8 Solving Radical Equations and Inequalities Example 5 Continued Method 2 Use algebra to solve the inequality. Step 2 Consider the radicand. 2 x – 6 ≥ 0 2 x ≥ 6 The radicand cannot be negative. Solve for x. x≥ 3 The solution of 21, or 3 ≤ x ≤ 21. Holt Algebra 2 is x ≥ 3 and x ≤

Solving Radical Equations and Inequalities 8 -8 Check It Out! Example 5 a Solve . Method 1 Use a graph and a table. On a graphing calculator, let Y 1 = and Y 2 = 5. The graph of Y 1 is at or below the graph of Y 2 for values of x between 3 and 12. Notice that Y 1 is undefined when < 3. The solution is 3 ≤ x ≤ 12. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 5 a Continued Method 2 Use algebra to solve the inequality. Step 1 Solve for x. Subtract 2. Square both sides. Simplify. x– 3≤ 9 x ≤ 12 Holt Algebra 2 Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 5 a Continued Method 2 Use algebra to solve the inequality. Step 2 Consider the radicand. x– 3≥ 0 The radicand cannot be negative. x≥ 3 The solution of 12, or 3 ≤ x ≤ 12. Holt Algebra 2 Solve for x. is x ≥ 3 and x ≤

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 5 b Solve . Method 1 Use a graph and a table. On a graphing calculator, let Y 1 = and Y 2 = 1. The graph of Y 1 is at or above the graph of Y 2 for values of x greater than – 1. Notice that Y 1 is undefined when < – 2. The solution is x ≥ – 1. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 5 b Continued Method 2 Use algebra to solve the inequality. Step 1 Solve for x. Cube both sides. x+2≥ 1 x ≥ – 1 Holt Algebra 2 Solve for x.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 5 b Continued Method 2 Use algebra to solve the inequality. Step 2 Consider the radicand. x+2≥ 1 x ≥ – 1 The solution of Holt Algebra 2 The radicand cannot be negative. Solve for x. is x ≥ – 1.

8 -8 Solving Radical Equations and Inequalities Example 6: Automobile Application The time t in seconds that it takes a car to travel a quarter mile when starting from a full stop can be estimated by using the formula , where w is the weight of the car in pounds and P is the power delivered by the engine in horsepower. If the quarter-mile time from a 3590 lb car is 13. 4 s, how much power does its engine deliver? Round to the nearest horsepower. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Example 6 Continued Use the formula to determine the amount of horsepower the 3590 lb car has if it finishes the quarter-mile in 13. 4 s. Substitute 13. 4 for t and 3590 for w. Cube both sides. Simplify. 2406. 104 P ≈ 709, 548. 747 P ≈ 295 Holt Algebra 2 Solve for P. The engine delivers a power of about 295 hp.

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 6 The speed s in miles per hour that a car is traveling when it goes into a skid can be estimated by using the formula s = 30 fd , where f is the coefficient of friction and d is the length of the skid marks in feet. A car skids to a stop on a street with a speed limit of 30 mi/h. The skid marks measure 35 ft, and the coefficient of friction was 0. 7. Was the car speeding? Explain. Use the formula to determine the greatest possible length of the driver’s skid marks if he was traveling 30 mi/h. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Check It Out! Example 6 Continued Substitute 30 for s and 0. 7 for f. Simplify. Square both sides. 900 = 21 d 43 ≈ d Simplify. Solve for d. If the car were traveling 30 mi/h, its skid marks would have measured about 43 ft. Because the actual skid marks measure less than 43 ft, the car was not speeding. Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Lesson Quiz: Part I Solve each equation or inequality. 1. x = 16 2. x = – 5 3. x=2 4. x = 14 5. x ≥ 59 Holt Algebra 2

8 -8 Solving Radical Equations and Inequalities Lesson Quiz: Part II 6. The radius r in feet of a spherical water tank can be determined by using the formula where V is the volume of the tank in cubic feet. To the nearest cubic foot, what is the volume of a spherical tank with a radius of 32 ft? 137, 258 ft 3 Holt Algebra 2 ,
 Inequalities with radicals
Inequalities with radicals Radical equations and inequalities
Radical equations and inequalities Solving radical equations and inequalities
Solving radical equations and inequalities Lesson 7 - graphing radical equations and inequalities
Lesson 7 - graphing radical equations and inequalities Radical equations and inequalities
Radical equations and inequalities Unit 6 test study guide radical functions answer key
Unit 6 test study guide radical functions answer key How to solve square root equations
How to solve square root equations Solving square root and other radical equations
Solving square root and other radical equations Solving square root and other radical equations
Solving square root and other radical equations Lesson 26 solving rational equations
Lesson 26 solving rational equations Solve the rational equation 8/x+1/5=3/x
Solve the rational equation 8/x+1/5=3/x Rational inequality
Rational inequality Solving multi step equations and inequalities
Solving multi step equations and inequalities Solving equations and inequalities
Solving equations and inequalities Solving equations and inequalities
Solving equations and inequalities Rational equation and rational inequalities
Rational equation and rational inequalities Logarithmic equation and inequalities
Logarithmic equation and inequalities 5-5 solving rational equations and inequalities
5-5 solving rational equations and inequalities Solving inequalities jeopardy
Solving inequalities jeopardy Solving equations and inequalities jeopardy
Solving equations and inequalities jeopardy 5-3 solving multi-step inequalities
5-3 solving multi-step inequalities Linear equation and inequalities
Linear equation and inequalities 1-2 lesson quiz solving linear equations
1-2 lesson quiz solving linear equations Lesson 3-2 solving inequalities answers
Lesson 3-2 solving inequalities answers Equations jeopardy
Equations jeopardy Equations inequalities and problem solving
Equations inequalities and problem solving Chapter 1 equations and inequalities
Chapter 1 equations and inequalities Logarithmic function equation and inequalities
Logarithmic function equation and inequalities Assignment 9 solving inequalities
Assignment 9 solving inequalities Lesson 4-2 absolute value inequalities
Lesson 4-2 absolute value inequalities Solving rational equations and inequalities
Solving rational equations and inequalities Algebra 2 chapter 1 equations and inequalities answer key
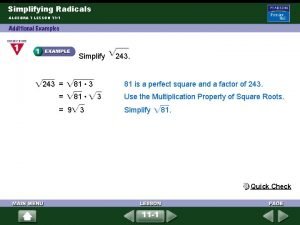
Algebra 2 chapter 1 equations and inequalities answer key 11-1 simplifying radical expressions answers
11-1 simplifying radical expressions answers Extraneous definition math
Extraneous definition math Upadd
Upadd How to solve radical equations
How to solve radical equations Solving radical equations with variables on both sides
Solving radical equations with variables on both sides Solving equations warm up
Solving equations warm up Mixed radical to entire radical
Mixed radical to entire radical Entire radical form
Entire radical form 7-5 exponential and logarithmic equations and inequalities
7-5 exponential and logarithmic equations and inequalities 7-5 exponential and logarithmic equations and inequalities
7-5 exponential and logarithmic equations and inequalities Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Radical and rational equations
Radical and rational equations Unit 6 radical functions homework 4 rational exponents
Unit 6 radical functions homework 4 rational exponents How to graph inequalities on a number line
How to graph inequalities on a number line Linear inequalities worksheet
Linear inequalities worksheet Solving two step inequalities
Solving two step inequalities A pair of inequalities joined by and or or
A pair of inequalities joined by and or or Solving inequalities using addition and subtraction
Solving inequalities using addition and subtraction