1 5 Solving Inequalities Solve and graph inequalities








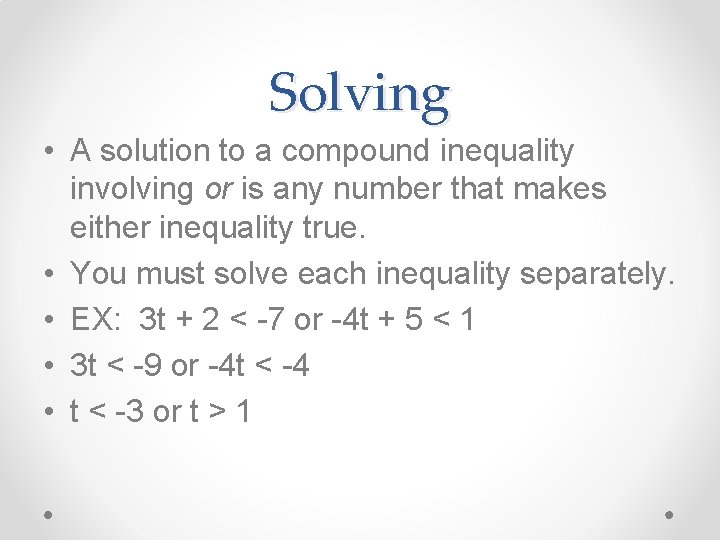

- Slides: 11

1 -5 Solving Inequalities Solve and graph inequalities by using properties of inequalities.

Graphing Inequalities • Open dot for < or > • Closed dot for ≥ or ≤ • If the inequality symbol is open toward the variable, shade to the right. • If the inequality symbol is pointed toward the variable, shade to the left.

Properties of Inequalities • If you multiply or divide both sides of an inequality by a negative number, the symbol flips.

Solving •

No Solution or All Real Numbers • There is no solution if all variables cancel and the statement is false. o Ex: -2 > 7 (no variables and we know that -2 is not greater than 7) • All real numbers are solutions if all variables cancel and the statement is true. o Ex: -15 ≤ 8 (no variables and it is true that -15 is less than 8) o Same as infinitely many solutions
Compound Inequality • Consists of two distinct inequalities joined by the word and or the word or

Using the word “And” • Contains the overlap of the graphs of two inequalities that form a compound inequality. • EX: x ≥ 3 and x ≤ 7 • Can also be written 3 ≤ x ≤ 7 o This is only for a compound inequality using the word “and”

Using the word “Or” • Contains each graph of the two inequalities that form the compound inequality. • Used when there is no overlap. • EX: x < -2 or x ≥ 1

Solving • A solution to a compound inequality involving and is any number that makes both inequalities true. • EX: -3 ≤ m – 4 < -1 • Isolate the variable by adding 4 to each piece • -3 + 4 ≤ m – 4 + 4 < -1 + 4 • 1 ≤ m < 3
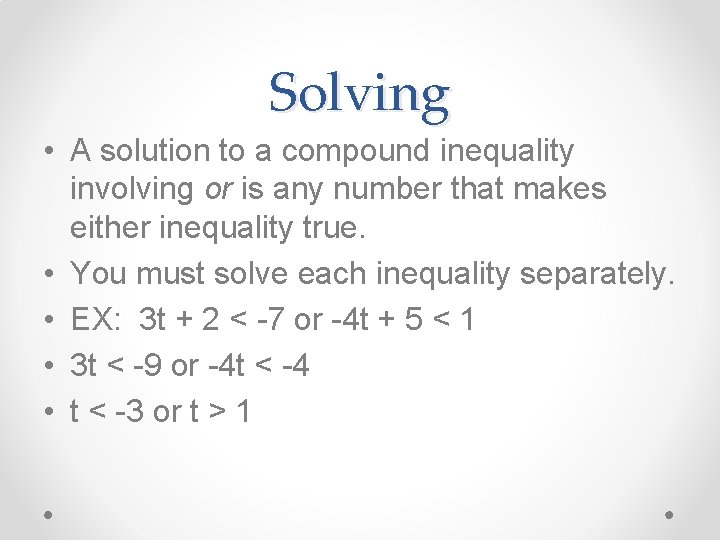
Solving • A solution to a compound inequality involving or is any number that makes either inequality true. • You must solve each inequality separately. • EX: 3 t + 2 < -7 or -4 t + 5 < 1 • 3 t < -9 or -4 t < -4 • t < -3 or t > 1

Assignment • Odds p. 38 #27 -31, 39 -43