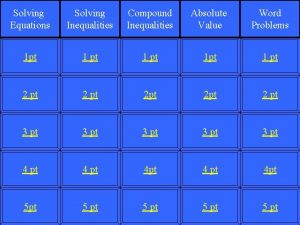
Solving Linear Equations and 2 1 Inequalities Solving








































- Slides: 41

Solving Linear Equations and 2 -1 Inequalities Solving Linear Equations and Inequalities Warm Up Lesson Presentation Lesson Quiz Holt Algebra 22

2 -1 Solving Linear Equations and Inequalities Warm Up Simplify each expression. 2. –(w – 2) –w + 2 1. 2 x + 5 – 3 x –x + 5 3. 6(2 – 3 g) 12 – 18 g Graph on a number line. 4. t > – 2 – 4 – 3 – 2 – 1 0 1 2 3 4 5 5. Is 2 a solution of the inequality – 2 x < – 6? Explain. No; when 2 is substituted for x, the inequality is false: – 4 < – 6 Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Objectives Solve linear equations using a variety of methods. Solve linear inequalities. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Vocabulary equation solution set of an equation linear equation in one variable identify contradiction inequality Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities An equation is a mathematical statement that two expressions are equivalent. The solution set of an equation is the value or values of the variable that make the equation true. A linear equation in one variable can be written in the form ax = b, where a and b are constants and a ≠ 0. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Linear Equations in One variable 4 x = 8 3 x – = – 9 2 x – 5 = 0. 1 x +2 Nonlinear Equations + 1 = 32 + 1 = 41 3 – 2 x = – 5 Notice that the variable in a linear equation is not under a radical sign and is not raised to a power other than 1. The variable is also not an exponent and is not in a denominator. Solving a linear equation requires isolating the variable on one side of the equation by using the properties of equality. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities To isolate the variable, perform the inverse or opposite of every operation in the equation on both sides of the equation. Do inverse operations in the reverse order of operations. Holt Algebra 2

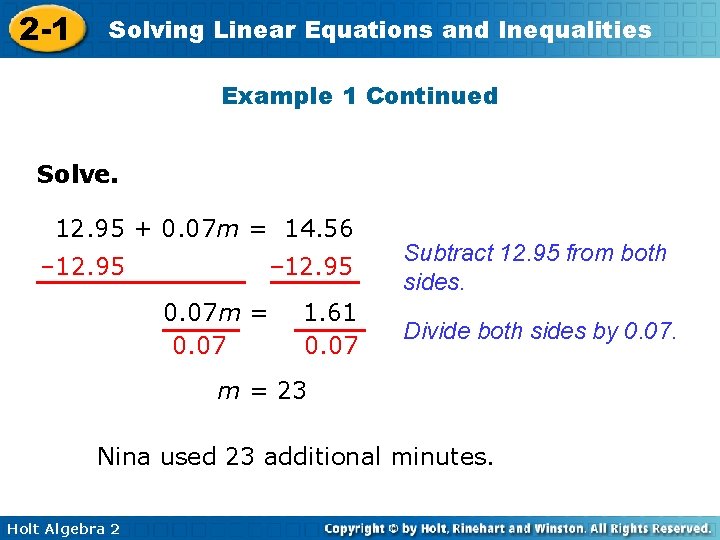
2 -1 Solving Linear Equations and Inequalities Example 1: Consumer Application The local phone company charges $12. 95 a month for the first 200 of air time, plus $0. 07 for each additional minute. If Nina’s bill for the month was $14. 56, how many additional minutes did she use? Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 1 Continued Let m represent the number of additional minutes that Nina used. Model monthly plus charge 12. 95 Holt Algebra 2 + additional minute charge times 0. 07 * number of additional = total charge minutes m = 14. 56

2 -1 Solving Linear Equations and Inequalities Example 1 Continued Solve. 12. 95 + 0. 07 m = 14. 56 – 12. 95 0. 07 m = 0. 07 1. 61 0. 07 Subtract 12. 95 from both sides. Divide both sides by 0. 07. m = 23 Nina used 23 additional minutes. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Stacked cups are to be placed in a pantry. One cup is 3. 25 in. high and each additional cup raises the stack 0. 25 in. How many cups fit between two shelves 14 in. apart? Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Continued Let c represent the number of additional cups needed. Model additional cup one cup plus height 3. 25 Holt Algebra 2 + 0. 25 times * number of total additional = height cups c = 14. 00

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 1 Continued Solve. 3. 25 + 0. 25 c = 14. 00 – 3. 25 0. 25 c = 10. 75 0. 25 Subtract 3. 25 from both sides. Divide both sides by 0. 25. c = 43 44 cups fit between the 14 in. shelves. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 2: Solving Equations with the Distributive Property Solve 4(m + 12) = – 36 Method 1 The quantity (m + 12) is multiplied by 4, so divide by 4 first. 4(m + 12) = – 36 4 4 m + 12 = – 9 – 12 m = – 21 Holt Algebra 2 Divide both sides by 4. Subtract 12 from both sides.

2 -1 Solving Linear Equations and Inequalities Example 2 Continued Check 4(m + 12) = – 36 4(– 21 + 12) 4(– 9) – 36 Holt Algebra 2 – 36

2 -1 Solving Linear Equations and Inequalities Example 2 Continued Solve 4(m + 12) = – 36 Method 2 Distribute before solving. 4 m + 48 = – 36 – 48 Distribute 4. Subtract 48 from both sides. 4 m = – 84 4 m – 84 = 4 4 m = – 21 Holt Algebra 2 Divide both sides by 4.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Solve 3(2 – 3 p) = 42. Method 1 The quantity (2 – 3 p) is multiplied by 3, so divide by 3 first. 3(2 – 3 p) = 42 3 3 2 – 3 p = 14 – 2 – 3 p = 12 – 3 p = – 4 Holt Algebra 2 Divide both sides by 3. Subtract 2 from both sides. Divide both sides by – 3.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Continued Check 3(2 – 3 p) = 42 3(2 + 12) 6 + 36 42 Holt Algebra 2 42 42 42

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 a Continued Solve 3(2 – 3 p) = 42. Method 2 Distribute before solving. 6 – 9 p = 42 – 6 – 9 p = 36 – 9 p 36 = – 9 p = – 4 Holt Algebra 2 Distribute 3. Subtract 6 from both sides. Divide both sides by – 9.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Solve – 3(5 – 4 r) = – 9. Method 1 The quantity (5 – 4 r) is multiplied by – 3, so divide by – 3 first. – 3(5 – 4 r) = – 9 – 3 5 – 4 r = 3 – 5 – 4 r = – 2 Holt Algebra 2 Divide both sides by – 3. Subtract 5 from both sides.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Continued Solve – 3(5 – 4 r) = – 9. Method 1 – 4 r – 2 – 4 r= Divide both sides by – 4. = Check – 3(5 – 4 r) = – 9 – 3(5 – 4 • ) – 9 – 3(5 – 2) – 3(3) – 9 Holt Algebra 2 – 9 – 9

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 2 b Continued Solve – 3(5 – 4 r) = – 9. Method 2 Distribute before solving. – 15 + 12 r = – 9 +15 12 r = 6 12 r 6 = 12 12 r= Holt Algebra 2 Distribute 3. Add 15 to both sides. Divide both sides by 12.

2 -1 Solving Linear Equations and Inequalities If there are variables on both sides of the equation, (1) simplify each side. (2) collect all variable terms on one side and all constants terms on the other side. (3) isolate the variables as you did in the previous problems. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 3: Solving Equations with Variables on Both Sides Solve 3 k– 14 k + 25 = 2 – 6 k – 12. Simplify each side by combining – 11 k + 25 = – 6 k – 10 like terms. +11 k Collect variables on the right side. Add. 25 = 5 k – 10 Collect constants on the left side. +10 + 10 35 = 5 k 5 5 7=k Holt Algebra 2 Isolate the variable.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 3 Solve 3(w + 7) – 5 w = w + 12. Simplify each side by combining – 2 w + 21 = w + 12 like terms. +2 w Collect variables on the right side. 21 = – 12 9 3 Holt Algebra 2 3 w + 12 – 12 = 3 w 3 3=w Add. Collect constants on the left side. Isolate the variable.

2 -1 Solving Linear Equations and Inequalities You have solved equations that have a single solution. Equations may also have infinitely many solutions or no solution. An equation that is true for all values of the variable, such as x = x, is an identity. An equation that has no solutions, such as 3 = 5, is a contradiction because there are no values that make it true. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 A: Identifying Identities and Contractions Solve 3 v – 9 – 4 v = –(5 + v) – 9 – v = – 5 – v +v +v – 9 ≠ – 5 x Simplify. Contradiction The equation has no solution. The solution set is the empty set, which is represented by the symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 4 B: Identifying Identities and Contractions Solve 2(x – 6) = – 5 x – 12 + 7 x Simplify. 2 x – 12 = 2 x – 12 – 2 x – 12 = – 12 Identity The solutions set is all real number, or . Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 a Solve 5(x – 6) = 3 x – 18 + 2 x 5 x – 30 = 5 x – 18 – 5 x Simplify. – 5 x – 30 ≠ – 18 x Contradiction The equation has no solution. The solution set is the empty set, which is represented by the symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 4 b Solve 3(2 – 3 x) = – 7 x – 2(x – 3) 6 – 9 x = – 9 x + 6 Simplify. + 9 x +9 x 6=6 Identity The solutions set is all real numbers, or . Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities An inequality is a statement that compares two expressions by using the symbols <, >, ≤, ≥, or ≠. The graph of an inequality is the solution set, the set of all points on the number line that satisfy the inequality. The properties of equality are true for inequalities, with one important difference. If you multiply or divide both sides by a negative number, you must reverse the inequality symbol. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities These properties also apply to inequalities expressed with >, ≥, and ≤. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Helpful Hint To check an inequality, test • the value being compared with x • a value less than that, and • a value greater than that. Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Example 5: Solving Inequalities Solve and graph 8 a – 2 ≥ 13 a + 8 – 13 a – 5 a – 2 ≥ 8 +2 +2 – 5 a ≥ 10 – 5 a ≤ 10 – 5 a ≤ – 2 Holt Algebra 2 Subtract 13 a from both sides. Add 2 to both sides. Divide both sides by – 5 and reverse the inequality.

2 -1 Solving Linear Equations and Inequalities Example 5 Continued Solve and graph 8 a – 2 ≥ 13 a + 8. Check Test values in the original inequality. Test x = – 4 • – 10 – 9 Test x = – 2 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 Test x = – 1 8(– 4) – 2 ≥ 13(– 4) + 8 8(– 2) – 2 ≥ 13(– 2) + 8 8(– 1) – 2 ≥ 13(– 1) + 8 – 34 ≥ – 44 So – 4 is a solution. Holt Algebra 2 – 18 ≥ – 18 So – 2 is a solution. – 10 ≥ – 5 x So – 1 is not a solution.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 5 Solve and graph x + 8 ≥ 4 x + 17 –x –x 8 ≥ 3 x +17 – 9 ≥ 3 x 3 3 – 3 ≥ x or x ≤ – 3 Holt Algebra 2 Subtract x from both sides. Subtract 17 from both sides. Divide both sides by 3.

2 -1 Solving Linear Equations and Inequalities Check It Out! Example 5 Continued Solve and graph x + 8 ≥ 4 x + 17. Check Test values in the original inequality. Test x = – 6 • – 6 – 5 Test x = – 3 – 6 + 8 ≥ 4(– 6) + 17 – 3 +8 ≥ 4(– 3) + 17 2 ≥ – 7 So – 6 is a solution. Holt Algebra 2 5≥ 5 So – 3 is a solution. – 4 – 3 – 2 – 1 0 1 2 3 Test x = 0 0 +8 ≥ 4(0) + 17 8 ≥ 17 x So 0 is not a solution.

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part I 1. Alex pays $19. 99 for cable service each month. He also pays $2. 50 for each movie he orders through the cable company’s pay-per-view service. If his bill last month was $32. 49, how many movies did Alex order? 5 movies Holt Algebra 2

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part II Solve. x=6 2. 2(3 x – 1) = 34 3. 4 y – 9 – 6 y = 2(y + 5) – 3 y = – 4 4. r + 8 – 5 r = 2(4 – 2 r) all real numbers, or 5. – 4(2 m + 7) = no solution, or Holt Algebra 2 (6 – 16 m)

2 -1 Solving Linear Equations and Inequalities Lesson Quiz: Part III 5. Solve and graph. 12 + 3 q > 9 q – 18 q<5 ° – 2 – 1 Holt Algebra 2 0 1 2 3 4 5 6 7
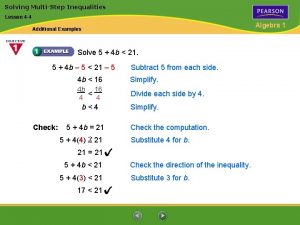
 5-3 solving multi-step inequalities
5-3 solving multi-step inequalities 2-1 solving linear equations and inequalities
2-1 solving linear equations and inequalities 2-1 solving linear equations and inequalities
2-1 solving linear equations and inequalities 1-5 solving inequalities answers
1-5 solving inequalities answers Lesson 26 solving rational equations
Lesson 26 solving rational equations Solve the rational equation 8/x+1/5=3/x
Solve the rational equation 8/x+1/5=3/x Rational inequality
Rational inequality Solve radical inequalities
Solve radical inequalities Solving radical equations and inequalities
Solving radical equations and inequalities Solving multi step equations and inequalities
Solving multi step equations and inequalities How to solve inequalities
How to solve inequalities Equations and inequalities
Equations and inequalities Solving radical equations and inequalities
Solving radical equations and inequalities How to solve rational equations and inequalities
How to solve rational equations and inequalities 4-5 exponential and logarithmic equations and inequalities
4-5 exponential and logarithmic equations and inequalities 5-5 solving rational equations and inequalities
5-5 solving rational equations and inequalities Inequality jeopardy
Inequality jeopardy Equations and inequalities jeopardy
Equations and inequalities jeopardy Solving inequalities jeopardy
Solving inequalities jeopardy Equations inequalities and problem solving
Equations inequalities and problem solving College algebra equations and inequalities
College algebra equations and inequalities Exponential and logarithmic inequalities
Exponential and logarithmic inequalities 1-5 solving equations and inequalities by graphing
1-5 solving equations and inequalities by graphing Lesson 1-4 solving absolute value equations
Lesson 1-4 solving absolute value equations Solving rational equation and inequalities
Solving rational equation and inequalities Algebra 2 equations and inequalities
Algebra 2 equations and inequalities Unit 2 reasoning with linear equations and inequalities
Unit 2 reasoning with linear equations and inequalities 5-6 graphing inequalities in two variables answer key
5-6 graphing inequalities in two variables answer key Solving systems of linear inequalities by graphing
Solving systems of linear inequalities by graphing Absolute value inequalities and vs or
Absolute value inequalities and vs or How to solve linear inequalities word problems
How to solve linear inequalities word problems Pick out the greater number in each pair
Pick out the greater number in each pair Solving linear inequalities hangman
Solving linear inequalities hangman Solving linear inequalities worksheet
Solving linear inequalities worksheet System of inequalities quiz part 1
System of inequalities quiz part 1 Linear inequality in one variable example
Linear inequality in one variable example 6-6 solving systems of linear inequalities
6-6 solving systems of linear inequalities Forming equations worksheet
Forming equations worksheet Solving
Solving Building and solving equations
Building and solving equations Solving systems of linear and quadratic equations
Solving systems of linear and quadratic equations Forming and solving equations worksheet
Forming and solving equations worksheet