2 8 Solving TwoStep Equations Warm Up Problem

2 -8 Solving. Two-Step. Equations Warm Up Problem of the Day Lesson Presentation Course 33

2 -8 Solving Two-Step Equations Warm Up Solve. 1. x + 12 = 35 x = 23 2. 8 x = 120 x = 15 y 3. =7 9 y = 63 4. – 34 = y + 56 y = – 90 Course 3

2 -8 Solving Two-Step Equations Problem of the Day x is an odd integer. If you triple x and then subtract 7, you get a prime number. What is the smallest possible x? (Hint: What is the smallest prime number? ) x=3 Course 3

2 -8 Solving Two-Step Equations Learn to solve two-step equations. Course 3

2 -8 Solving Two-Step Equations Sometimes more than one inverse operation is needed to solve an equation. Before solving, ask yourself, “What is being done to the variable, and in what order? ” Then work backward to undo the operations. Course 3

2 -8 Solving Two-Step Equations Additional Example 1: Problem Solving Application The mechanic’s bill to repair Mr. Wong’s car was $650. The mechanic charges $45 an hour for labor, and the parts that were used cost $443. How many hours did the mechanic work on the car? Course 3

2 -8 Solving Two-Step Equations Additional Example 1 Continued 1 Understand the Problem List the important information: The answer is the number of hours the mechanic worked on the car. • The parts cost $443. • The labor cost $45 per hour. • The total bill was $650. Let h represent the hours the mechanic worked. Total bill = Parts + Labor 650 = 443 + 45 h Course 3

2 -8 Solving Two-Step Equations Additional Example 1 Continued 2 Make a Plan Think: First the variable is multiplied by 45, and then 443 is added to the result. Work backward to solve the equation. Undo the operations in reverse order: First subtract 443 from both sides of the equation, and then divide both sides of the new equation by 45. Course 3

2 -8 Solving Two-Step Equations Additional Example 1 Continued 3 Solve 650 = 443 + 45 h – 443 207 = 45 h 45 45 Subtract to undo the addition. 45 h Divide to undo multiplication. 4. 6 = h The mechanic worked for 4. 6 hours on Mr. Wong’s car. Course 3

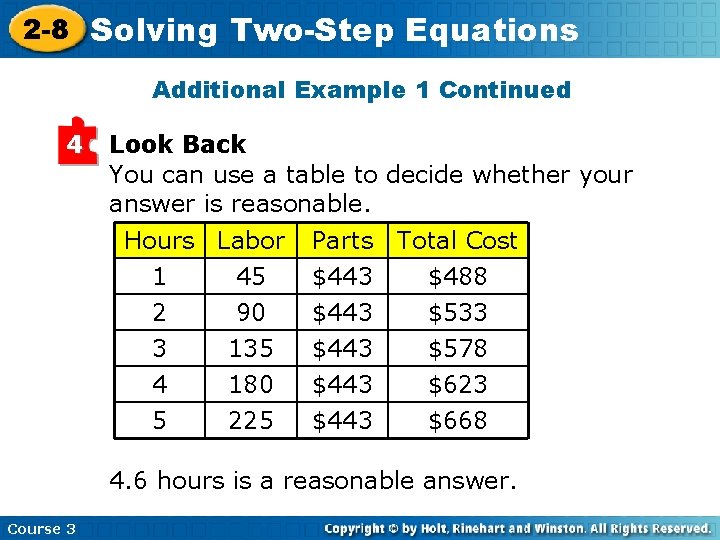
2 -8 Solving Two-Step Equations Additional Example 1 Continued 4 Look Back You can use a table to decide whether your answer is reasonable. Hours Labor 1 45 2 90 3 135 4 5 180 225 Parts $443 Total Cost $488 $533 $578 $443 $623 $668 4. 6 hours is a reasonable answer. Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 1 The mechanic’s bill to repair your car was $850. The mechanic charges $35 an hour for labor, and the parts that were used cost $275. How many hours did the mechanic work on your car? Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 1 Continued 1 Understand the Problem List the important information: The answer is the number of hours the mechanic worked on your car. • The parts cost $275. • The labor cost $35 per hour. • The total bill was $850. Let h represent the hours the mechanic worked. Total bill = Parts + Labor 850 = 275 + 35 h Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 1 Continued 2 Make a Plan Think: First the variable is multiplied by 35, and then 275 is added to the result. Work backward to solve the equation. Undo the operations in reverse order: First subtract 275 from both sides of the equation, and then divide both sides of the new equation by 35. Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 1 Continued 3 Solve 850 = 275 + 35 h – 275 575 = 35 h 35 35 Subtract to undo the addition. 35 h Divide to undo multiplication. 16. 4 h The mechanic worked for about 16. 4 hours on your car. Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 1 Continued 4 Look Back You can use a table to decide whether your answer is reasonable. Hours Labor 13 455 14 490 15 525 16 17 560 595 Parts $275 Total Cost $730 $765 $800 $275 $835 $870 16. 4 hours is a reasonable answer. Course 3

2 -8 Solving Two-Step Equations Additional Example 2 A: Solving Two-Step Equations n Solve + 7 = 22 3 Method 1: Work backward to isolate the variable. Think: First the variable is divided by 3, and then 7 is added. To isolate the variable, subtract 7, and then multiply by 3. n + 7 – 7 = 22 – 7 3 n 3 =3 3 n = 45 Course 3 15 Subtract 7 from both sides. Multiply both sides by 3.

2 -8 Solving Two-Step Equations Additional Example 2 A Continued Solve n + 7 = 22 3 Method 2: Multiply both sides of the equation by the denominator. (3) n + 7 = 22(3) 3 Multiply both sides by the denominator. n + 21 = 66 – 21 n Course 3 – 21 = 45 Subtract to undo addition.

2 -8 Solving Two-Step Equations Additional Example 2 B: Solving Two-Step Equations Solve y – 4 = 9 3 Method 1: Work backward to isolate the variable. y 4 Rewrite the expression as – =9 3 3 the sum of two fractions. 4 Think: First the variable is divided by 3, and then is 3 4 subtracted. To isolate the variable, add and then 3 multiply by 3. 4 y 4 4 4 Add to both sides. – + =9+ 3 3 31 y (3) = (3) Multiply both sides by 3. t 3 3 y = 31 Course 3

2 -8 Solving Two-Step Equations Additional Example 2 B: Solving Two-Step Equations Solve y – 4 = 9 3 Method 2: Multiply both sides of the equation by the denominator. y– 4 3 =9 (3) y – 4 = 9(3) 3 Multiply both sides by the denominator. y – 4 = 27 +4 +4 y = 31 Course 3 Add to undo subtraction.

2 -8 Solving Two-Step Equations Check It Out: Example 2 A n + 8 = 18 4 Method 1: Work backward to isolate the variable. Think: First the variable is divided by 4, and then 8 is added. To isolate the variable, subtract 8, and then multiply by 4. Solve n + 8 – 8 = 18 – 8 4 n 4 =4 4 n = 40 Course 3 10 Subtract 8 from both sides. Multiply both sides by 4.

2 -8 Solving Two-Step Equations Check It Out: Example 2 A Solve n + 8 = 18 4 Method 2: Multiply both sides of the equation by the denominator. (4) n + 8 = 18(4) 4 Multiply both sides by the denominator. n + 32 = 72 – 32 n Course 3 – 32 = 40 Subtract to undo addition.

2 -8 Solving Two-Step Equations Check It Out: Example 2 B Solve y – 7 = 7 2 Method 1: Work backward to isolate the variable. y 7 Rewrite the expression as – =7 2 2 the sum of two fractions. 7 Think: First the variable is divided by 2, and then is 2 7 subtracted. To isolate the variable, add and then 2 multiply by 2. 7 y 7 7 7 Add to both sides. – + =7+ 2 2 21 y (2) = (2) Multiply both sides by 2. t 2 2 y = 21 Course 3

2 -8 Solving Two-Step Equations Check It Out: Example 2 B Solve y – 7 = 7 2 Method 2: Multiply both sides of the equation by the denominator. y– 7 2 =7 (2) y – 7 = 7(2) 2 Multiply both sides by the denominator. y – 7 = 14 +7 +7 y = 21 Course 3 Add to undo subtraction.

2 -8 Solving Two-Step Equations Lesson Quiz Solve. x – 3 = 10 – 9 2. 7 y + 25 = – 24 1. x = – 117 y = – 7 3. – 8. 3 = – 3. 5 x + 13. 4 x = 6. 2 4. y + 5 = 3 11 y = 28 5. The cost for a new cell phone plan is $39 per month plus a one-time start-up fee of $78. If you are charged $1014, how many months will the contract last? 24 Course 3