1 5 Absolute Value Equations and Inequalities Algebra

1 -5 Absolute Value Equations and Inequalities Algebra 2

Algebra 2 Algebraic Definition of Absolute Value - If x > 0, then | x | = x - If x < 0. then | x | = -x

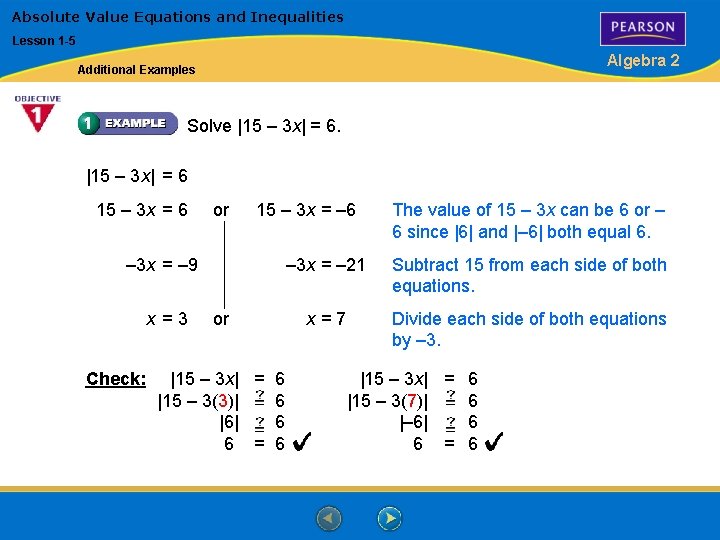
Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples Solve |15 – 3 x| = 6 15 – 3 x = 6 or 15 – 3 x = – 6 – 3 x = – 9 x =3 Check: or |15 – 3 x| = 6 |15 – 3(3)| 6 |6| 6 6 = 6 The value of 15 – 3 x can be 6 or – 6 since |6| and |– 6| both equal 6. – 3 x = – 21 Subtract 15 from each side of both equations. x=7 Divide each side of both equations by – 3. |15 – 3 x| = 6 |15 – 3(7)| 6 |– 6| 6 6 = 6

Algebra 2 You try: | 2 y - 6 | = 12

Algebra 2 Extraneous Solution: a solution of an equation derived from an original equation that is not a solution to the original equation. Extraneous Solution Video

Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples Solve 4 – 2|x + 9| = – 5 – 2|x + 9| = – 9 Add – 4 to each side. |x + 9| = 92 x + 9 = 92 or x + 9 = – 92 x = – 4. 5 or Check: x = – 13. 5 4 – 2 |x + 9| = – 5 4 – 2 |– 4. 5 + 9| – 5 4 – 2 |4. 5| – 5 4 – 2 (4. 5) – 5 = – 5 Divide each side by – 2. Rewrite as two equations. Subtract 9 from each side of both equations. 4 – 2|x + 9| = – 5 4 – 2 |– 13. 5 + 9| – 5 4 – 2 |– 4. 5| – 5 4 – 2 (4. 5) – 5 = – 5

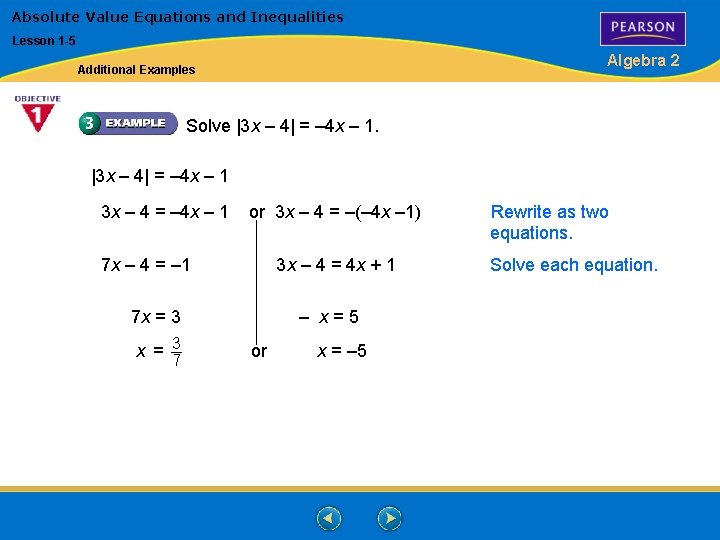
Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples Solve |3 x – 4| = – 4 x – 1 3 x – 4 = – 4 x – 1 or 3 x – 4 = –(– 4 x – 1) 7 x – 4 = – 1 3 x – 4 = 4 x + 1 7 x = 3 7 – x=5 or x = – 5 Rewrite as two equations. Solve each equation.

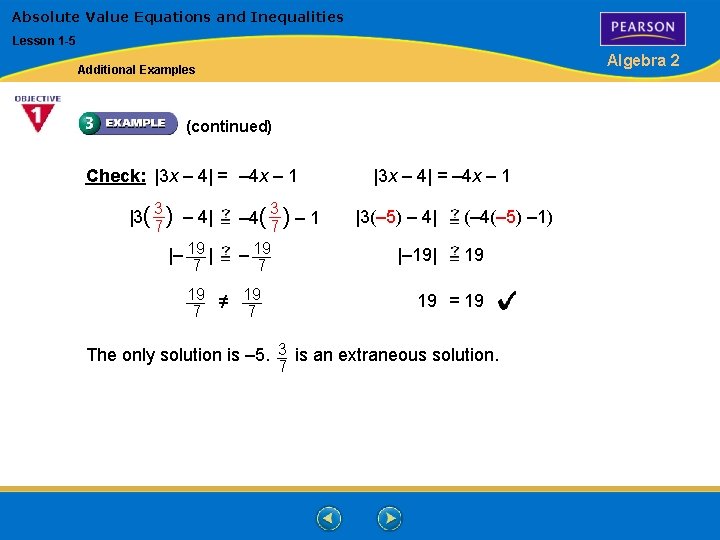
Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples (continued) Check: |3 x – 4| = – 4 x – 1 |3( 37 ) – 4| |– 19 | 7 3 – 4( 7 ) – 19 |3 x – 4| = – 4 x – 1 |3(– 5) – 4| |– 19| 7 19 =/ 19 7 7 (– 4(– 5) – 1) 19 19 = 19 The only solution is – 5. 3 is an extraneous solution. 7

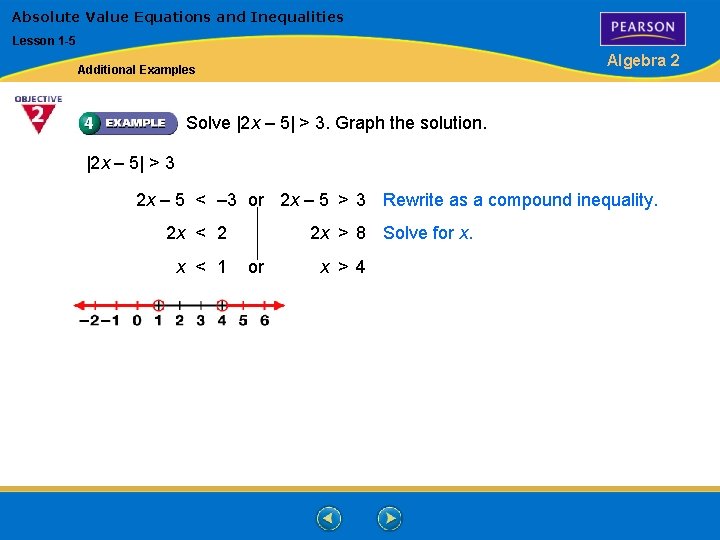
Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples Solve |2 x – 5| > 3. Graph the solution. |2 x – 5| > 3 2 x – 5 < – 3 or 2 x – 5 > 3 Rewrite as a compound inequality. 2 x < 2 x < 1 2 x > 8 Solve for x > 4

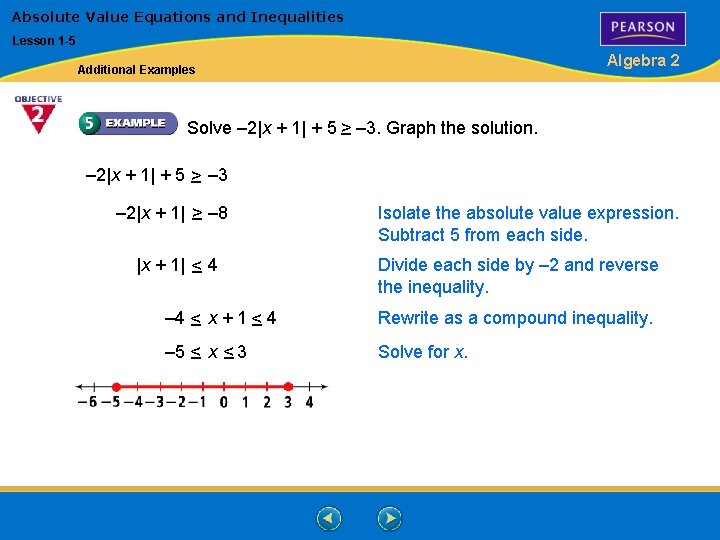
Absolute Value Equations and Inequalities Lesson 1 -5 Algebra 2 Additional Examples Solve – 2|x + 1| + 5 > – – 3. Graph the solution. – 2|x + 1| + 5 > – – 3 – 2|x + 1| > – – 8 |x + 1| < – 4 Isolate the absolute value expression. Subtract 5 from each side. Divide each side by – 2 and reverse the inequality. – 4 < – x + 1< – 4 Rewrite as a compound inequality. – 5 < –x< – 3 Solve for x.

Algebra 2 Homework pg 36 3 -27 every 3 rd