Solving Absolute Value Equations Inequalities Absolute Value of

Solving Absolute Value Equations & Inequalities
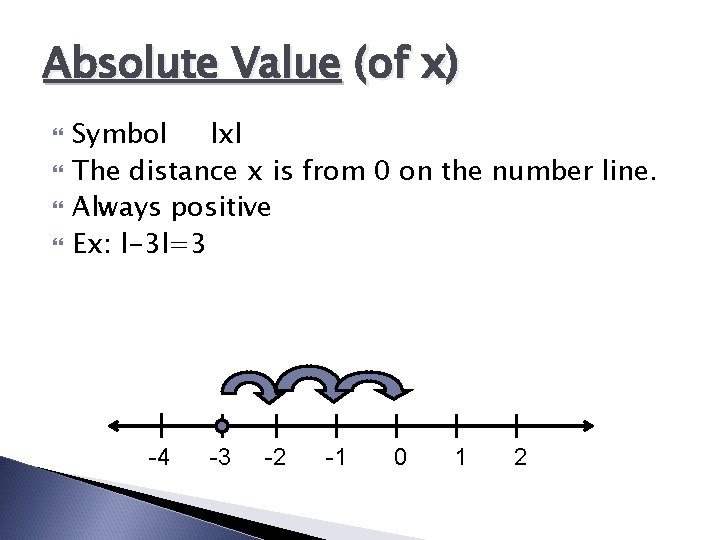
Absolute Value (of x) Symbol lxl The distance x is from 0 on the number line. Always positive Ex: l-3 l=3 -4 -3 -2 -1 0 1 2

Ex: |x| = 5 What are the possible values of x?

Solve the following |4 -8| |6 -4| |10+2| 2|6 -8| -4|-4+1|

To solve an absolute value equation: |ax+b | = c, where c>0 To solve, set up 2 new equations, then solve each equation. ax+b = c or ax+b = -c ** make sure the absolute value is by itself before you split to solve.

Ex: Solve |6 x-3| = 15

Ex: Solve |2 x + 7| -3 = 8

Abs Value Inequalities Absolute value inequalities can be represented by a conjunctions and disjunctions Three different ways |x|=a ◦ X=-a or x=a

AND with LESS THAN |x|<a AND statement X>-a AND x<a -a<x<a

OR with GREATER THAN |x|>a X<-a OR x>a

Solving abs value inequalities Isolate the absolute value Rewrite as a compound inequality ◦ AND for less than, less than or equal to ◦ OR for greater than, greater than or equal to These abs value inequalities only have one variable (x) so they get graphed on a number line

Solve |2 x+1|>5

Solve |4 x|+16>8

Solve •

Ex: Solve & graph.
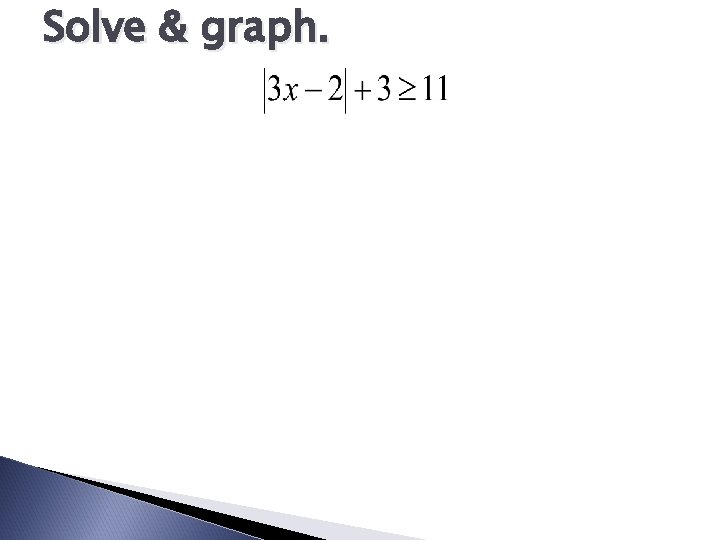
Solve & graph.

Solving Absolute Value Inequalities 1. |ax+b| < c, where c>0 Becomes an “and” problem Changes to: –c<ax+b<c 2. |ax+b| > c, where c>0 Becomes an “or” problem Changes to: ax+b>c or ax+b<-c
- Slides: 17