Solving Compound and Absolute Value Inequalities Chapter 1

Solving Compound and Absolute Value Inequalities Chapter 1 – Section 6

Compound Inequalities o o o Compound Inequality – a pair of inequalities joined by and or or Ex: -1 < x and x ≤ 3 which can be written as -1 < x ≤ 3 x < -1 or x ≥ 3 For and statements the value must satisfy both inequalities For or statements the value must satisfy one of the inequalities

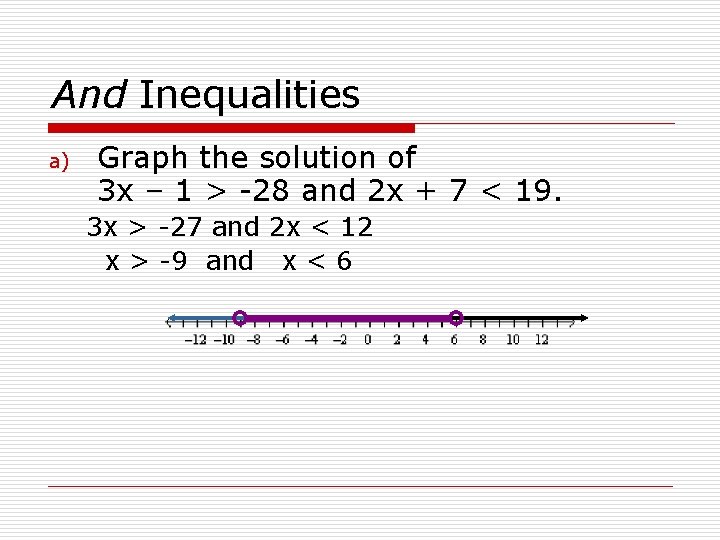
And Inequalities a) Graph the solution of 3 x – 1 > -28 and 2 x + 7 < 19. 3 x > -27 and 2 x < 12 x > -9 and x < 6

And Inequalities b)Graph the solution of -8 < 3 x + 1 <19 -9 < 3 x < 18 -3 < x < 6

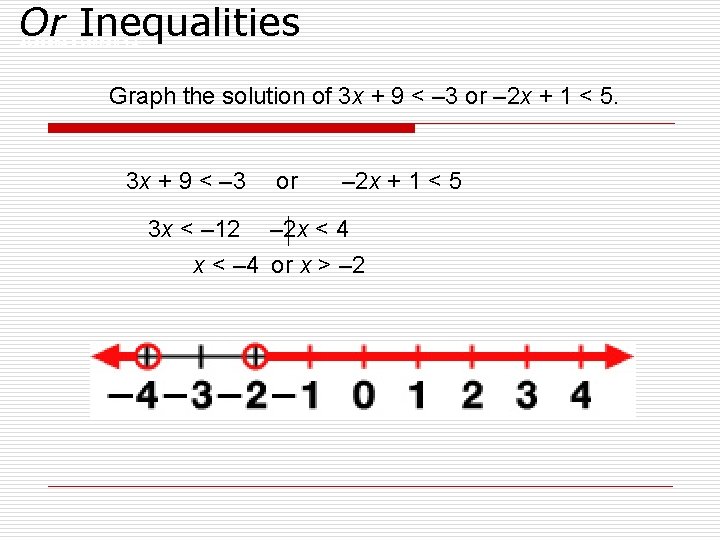
Or Inequalities ALGEBRA 2 LESSON 1 -4 Graph the solution of 3 x + 9 < – 3 or – 2 x + 1 < 5. 3 x + 9 < – 3 3 x < – 12 or – 2 x + 1 < 5 – 2 x < 4 x < – 4 or x > – 2

Try These Problems a) Graph the solution of 2 x > x + 6 and x – 7 < 2 a) x > 6 and x < 9 b) Graph the solution of x – 1 < 3 or x + 3 > 8 a) x < 4 or x > 11

Absolute Value Inequalities Let k represent a positive real number o │x │ ≥ k is equivalent to x ≤ -k or x ≥ k o │x │ ≤ k is equivalent to -k ≤ x ≤ k o Remember to isolate the absolute value before rewriting the problem with two inequalities

Solve |2 x – 5| > 3. Graph the solution. |2 x – 5| > 3 2 x – 5 < – 3 or 2 x – 5 > 3 2 x < 2 2 x > 8 x < 1 or x>4 Rewrite as a compound inequality. Solve for x.

Try This Problem Solve │2 x - 3 │ > 7 2 x – 3 > 7 2 x > 10 x>5 or or or 2 x – 3 < -7 2 x < -4 x < -2

Solve – 2|x + 1| + 5 > – – 3. Graph the solution. – 2|x + 1| + 5 > – – 3 – 2|x + 1| > – – 8 |x + 1| < – 4 Isolate the absolute value expression. Subtract 5 from each side. Divide each side by – 2 and reverse the inequality. – 4 < – x + 1< – 4 Rewrite as a compound inequality. – 5 < –x< – 3 Solve for x.

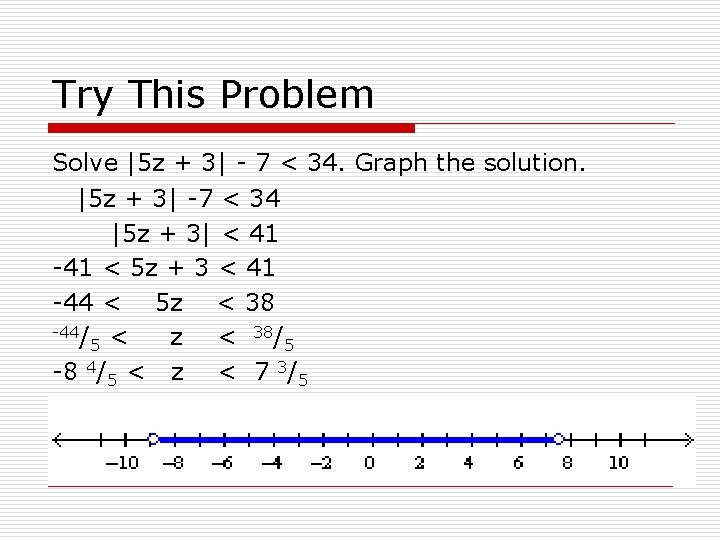
Try This Problem Solve |5 z + 3| - 7 < 34. Graph the solution. |5 z + 3| -7 < 34 |5 z + 3| < 41 -41 < 5 z + 3 < 41 -44 < 5 z < 38 -44/ < z < 38/5 5 -8 4/5 < z < 7 3/5

Homework p. 44 #27 - 40