Solving Inequalities Compound Inequalities and Absolute Value Inequalities

Solving Inequalities, Compound Inequalities and Absolute Value Inequalities Sec 1. 5 &1. 6 pg. 33 - 43

Objectives n The learner will be able to (TLWBAT): ¡ ¡ solve inequalities solve real-world problems with inequalities solve compound inequalities solve absolute value inequalities Hallford © 2007 Glencoe © 2003

Properties n Trichotomy Property ¡ For any two real numbers a and b, n

Properties of Inequalities n For any real number a, b, and c ¡ Addition Prop. n n ¡ Subtraction Prop. n n n If a>b, then a + c > b + c If a<b, then a + c < b + c If a>b, then a – c > b – c If a<b, then a – c < b – c See pg. 33 Hallford © 2007 Glencoe © 2003

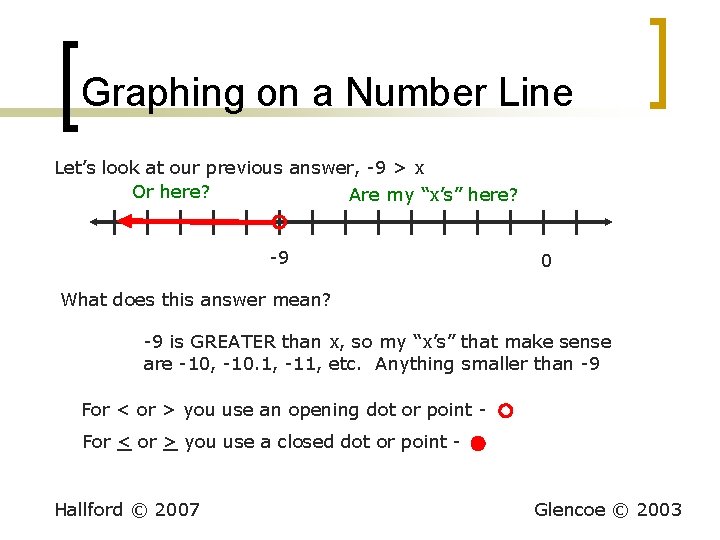
Graphing on a Number Line Let’s look at our previous answer, -9 > x Or here? Are my “x’s” here? -9 0 What does this answer mean? -9 is GREATER than x, so my “x’s” that make sense are -10, -10. 1, -11, etc. Anything smaller than -9 For < or > you use an opening dot or point For < or > you use a closed dot or point - Hallford © 2007 Glencoe © 2003

Properties of Inequalities n Multiplication Prop. ¡ ¡ ¡ ¡ n Division Prop. For any real numbers a, b, and c If c is positive If a>b, then ac>bc If a<b, then ac<bc ¡ If c is negative If a>b, then ac<bc If a<b, then ac>bc ¡ Hallford © 2007 ¡ ¡ ¡ For any real numbers a, b, and c If c is positive If a>b, then a/c>b/c If a<b, then a/c<b/c If c is negative If a>b, then a/c<b/c If a<b, then a/c>b/c Glencoe © 2003

Work this problem Now let’s graph 3 x – 7 < 7 x + 13 -7 x -4 x – 7 < 13 7 7 -4 x < 20 -4 -4 -5 0 You can also use set builder notation to express your answer. x > -5 {x | x > -5} This is read as the set of all x such that x is greater than or equal to -5 Hallford © 2007 Glencoe © 2003

Work this problem 3(a +4) – 2(3 a +4) ≤ 4 a - 1 3 a + 12 – 6 a – 8 ≤ 4 a – 1 Now graph and express in set builder notation. -3 a + 4 ≤ 4 a – 1 4 ≤ 7 a - 1 5 ≤ 7 a 5/ 7 ≤a 0 {a | a ≥ 5/7} You can also use interval notation. Interval notation uses ( & ) for < or > and [ & ] for ≤ & ≥. We also use -∞ (negative infinity) & +∞ (positive infinity) Interval notation for this problem would be [5/7, Hallford © 2007 +∞) Glencoe © 2003

Compound Inequalities n n A compound inequality consists of two inequalities joined by the word “and” or the word “or”. You must solve both inequalities and then graph. ¡ ¡ The final graph of the “and” inequality is the intersection of both individual solution graphs. The final graph of the “or” inequality in the union of both individual solution graphs Hallford © 2007 Glencoe © 2003

Let’s solve an “and” compound inequality 7 < 2 x - 1 < 15 “Means 7 < 2 x -1 and 2 x – 1< 15” Method 2 – Work together Method 1 – Divide into two problems 7 < 2 x – 1 8 < 2 x 4<x 2 x – 1 < 15 2 x < 16 x<8 7 < 2 x – 1 < 15 8 < 2 x < 16 4<x<8 Whatever you do to one side do to the other! 4<x Now Graph 0 4 8 x<8 { x | 4 ≤ x < 8} 4<x<8 Hallford © 2007 Glencoe © 2003

Let’s work about the same problem as an “or” inequality 7 < 2 x -1 or 2 x – 1 < 15 We know the answer is 4 < x and x < 8, but this time the answer graph is different. It is the UNION of the two graphs. 4<x 0 4 8 Glencoe © 2003 x<8 The solution set is all real numbers. 4 < x or x < 8 Hallford © 2007 0 0

Work this problem 2 x + 7 < -1 or 3 x + 7

Absolute Value Inequalities n |a| < b, where b > 0 ¡ ¡ n

Work these problems n n n |x – 1| < 3 -3 < x

Absolute Value Inequalities n |a| < b, where b < 0 ¡ n if b is less than zero, it is negative, so there is no solution |a| > b, where b < 0 ¡ if b is less than zero, it is negative, so every real number is a solution or all reals. Hallford © 2007 Glencoe © 2003

Work these problems |2 x – 7| < -5 There is no solution for the above since the absolute value cannot be less than zero. Hallford © 2007 |3 x – 1| + 9 > 2 |3 x – 1| > -7 Any value of “x” will make this statement true, since the absolute value is always greater than a negative number All Real numbers Glencoe © 2003