Absolute Value Systems of Inequalities Absolute Value Equations

Absolute Value & Systems of Inequalities Absolute Value Equations Absolute Value Inequalities Linear Inequalities

Absolute Value Equations and Inequalities Distance from zero to n on a real number line. |x| = 4 means, ‘ what number, x, are 4 units from zero on the number line. ’

Absolute Value Equations |u| = n If n is positive then u = n or u = -n Example: |x| = 2 ; x = 2 or x = -2 However, if n is negative then the equation has no real solution.

Practice Solve the equation a) |x + 7| = 4 b) 2|x - 5| + 6 = 20 c) |m - 4| + 12 = 8

Application Estella is driving from Savannah, Georgia to Washington D. C. Along the way, she will pass through Richmond VA. Estella’s distance from Richmond can be modeled by the function: D(t) = |460 – 60 t| Find the time when Estella will be 40 miles from Richmond.

Absolute Value Inequalities Inequality | x | < 5 , means all values of x that are less than 5 units from zero on the number line.

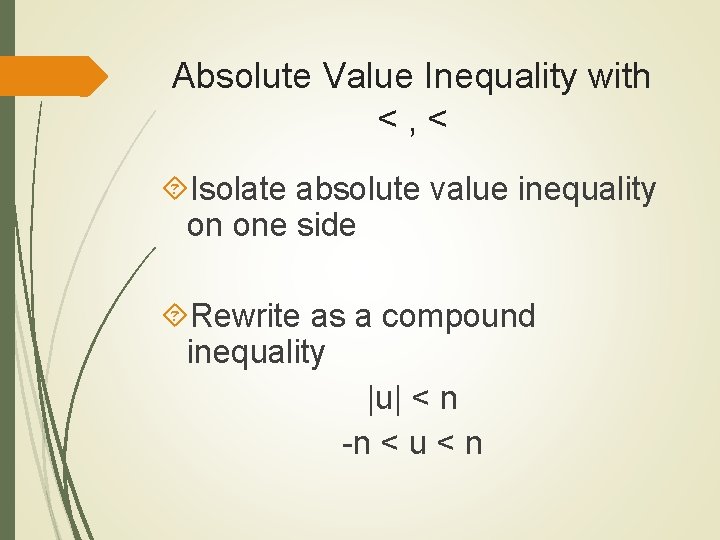
Absolute Value Inequality with <, < Isolate absolute value inequality on one side Rewrite as a compound inequality |u| < n -n < u < n

Absolute Value Inequality Solve the inequalities. Give the solution as an inequality and graph the solution set on a number line. a) |x - 4| < 6 b) |x + 3| + 8 < 10

Absolute Value Inequality > , > ‘Or’ Represents numbers further from zero |x | > 5

Absolute Value Inequality A person with high or low blood pressure will have a diastolic pressure (second number) that satisfies the inequality |D - 75| > 15 Where D is a person’s diastolic pressure in millimeters of mercury (mm. Hg). What is the high and low diastolic pressure?

Systems of Linear Inequalities Two or more constraints on a give situation. y>2 x– 3 Graph Solution What does the solution mean?

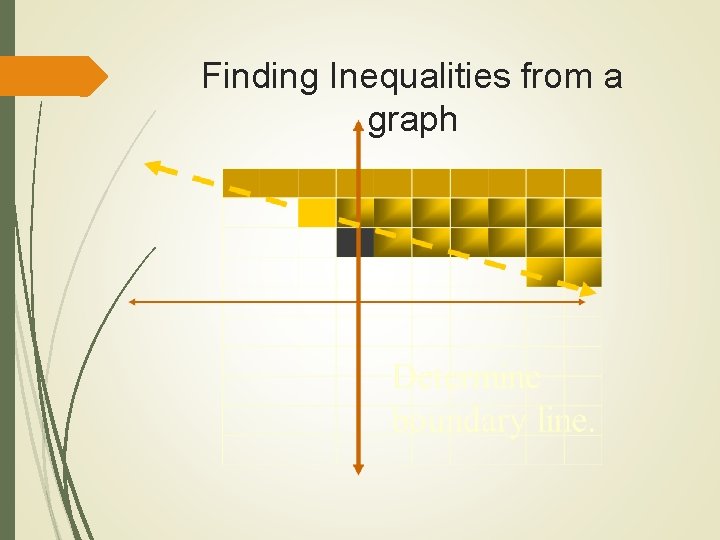
Finding Inequalities from a graph