Solving and Graphing Inequalities on a Number Line

Think About how we Solve Equations y+10 =16 What operation Is being done in this equation? Addition What is the inverse operation for addition? Subtraction y+10 =16 -10 y=6 y+ 10 = 16 (6)+10 = 16 16 = 16 Now Solve the equation using inverse operations Hold up – Check your work!

We Solve Inequalities the same way! y+10 < 16 What operation Is being done in this inequality? Addition What is the inverse operation for addition? Subtraction y+10 < 16 -10 y<6 y+ 10 < 16 (6)+10 < 16 16 = 16 Now Solve the equation using inverse operations Hold up – Check your work! Check an inequality the same way you do an equation, but the values that make the inequality will be more than one.

The solutions for these two problems mean different things! y+10 = 16 Y=6 y+10 < 16 Y<6 For the equation: Y can only be equal to 6! There is not another number that will make this equation true! For the inequality: Y can be more than one value, but the value must be less than 6.

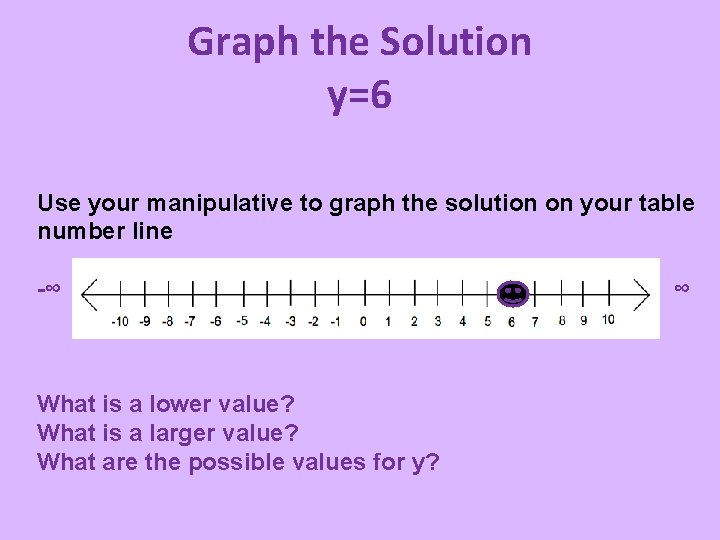
Graph the Solution y=6 Use your manipulative to graph the solution on your table number line -∞ What is a lower value? What is a larger value? What are the possible values for y? ∞

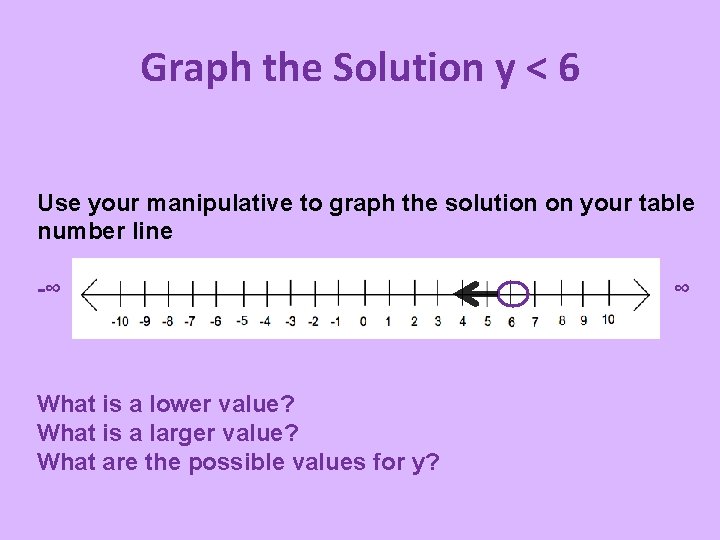
Graph the Solution y < 6 Use your manipulative to graph the solution on your table number line -∞ What is a lower value? What is a larger value? What are the possible values for y? ∞

Whoo. Hoooo!!! You just graphed the solution to an algebraic Inequality.

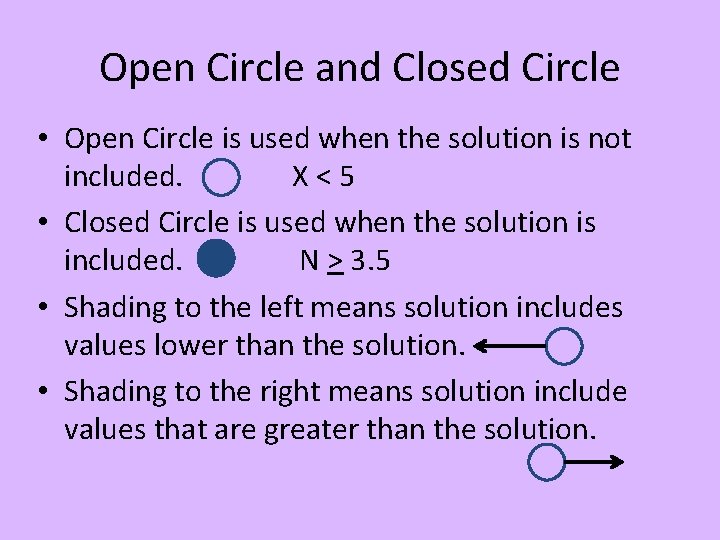
Open Circle and Closed Circle • Open Circle is used when the solution is not included. X<5 • Closed Circle is used when the solution is included. N > 3. 5 • Shading to the left means solution includes values lower than the solution. • Shading to the right means solution include values that are greater than the solution.

Graphing solutions on your own • You don’t have to create an entire number line each time you graph a solution BUT • You must always include: – the solution – lower value – higher value

Solve and graph the solution for 5 f>75 What operation is being done in the inequality? Multiplication What is the inverse operation for multiplication? Division 5 f > 75 5 5 f > 15 5 f>75 5(15) >75 75>75 Solve the inequality using inverse operations Check your work!!

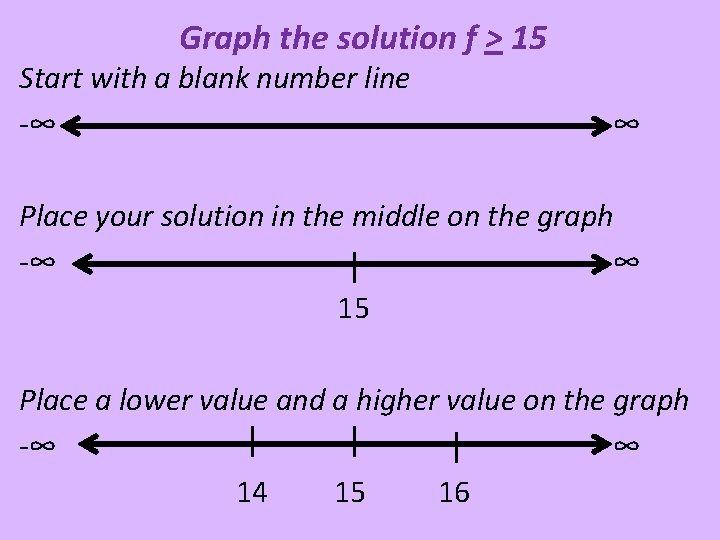
Graph the solution f > 15 Start with a blank number line -∞ ∞ Place your solution in the middle on the graph -∞ ∞ 15 Place a lower value and a higher value on the graph -∞ ∞ 14 15 16

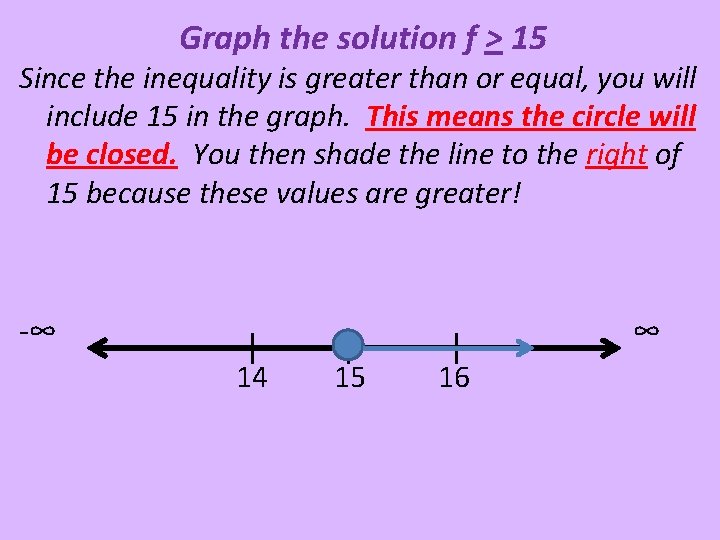
Graph the solution f > 15 Since the inequality is greater than or equal, you will include 15 in the graph. This means the circle will be closed. You then shade the line to the right of 15 because these values are greater! -∞ ∞ 14 15 16

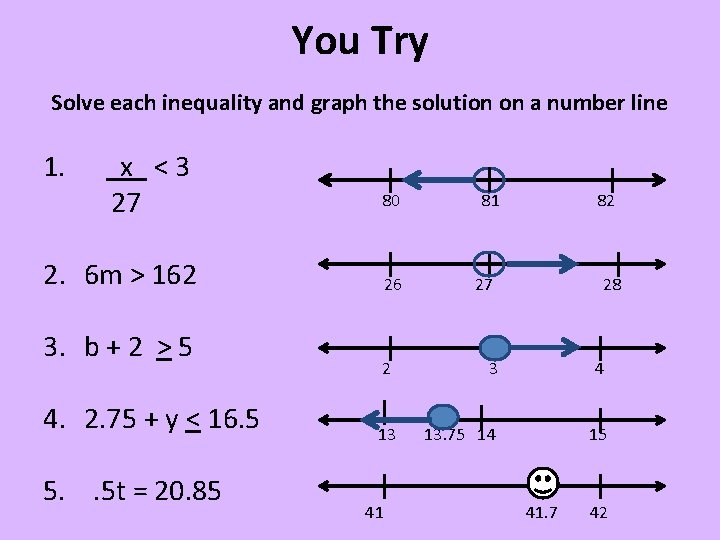
You Try Solve each inequality and graph the solution on a number line 1. x <3 27 80 2. 6 m > 162 3. b + 2 > 5 4. 2. 75 + y < 16. 5 5. . 5 t = 20. 85 26 81 82 27 28 2 3 4 13 13. 75 14 15 41 41. 7 42

You Try Solve each inequality and graph the solution on a number line 6. x ≠ 3 27 80 81 82