Chapter 7 Radical Equations Lesson 7 1 Operations






 = f[g(x)] – Plug in the full Composition of Functions l [f o g](x) = f[g(x)] – Plug in the full](https://slidetodoc.com/presentation_image_h/3222cbdff31555a196d767582cfc8f67/image-7.jpg)
 and [g o f](x) for f(x) = x+3 Examples l Find [f o g](x) and [g o f](x) for f(x) = x+3](https://slidetodoc.com/presentation_image_h/3222cbdff31555a196d767582cfc8f67/image-8.jpg)



























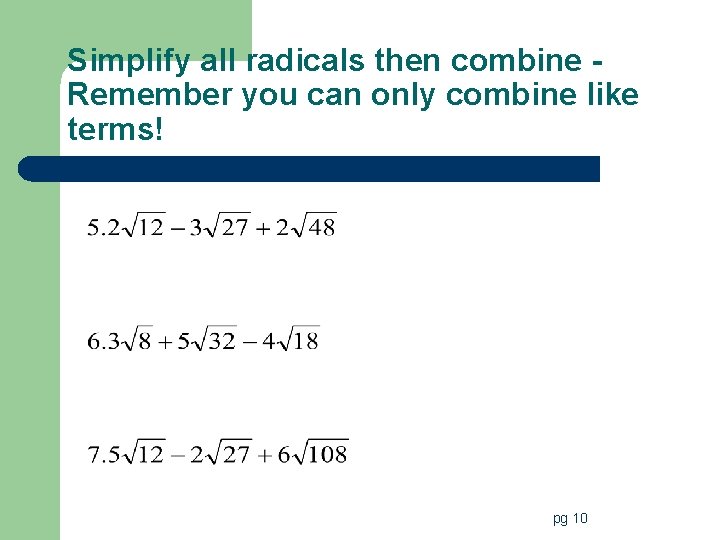







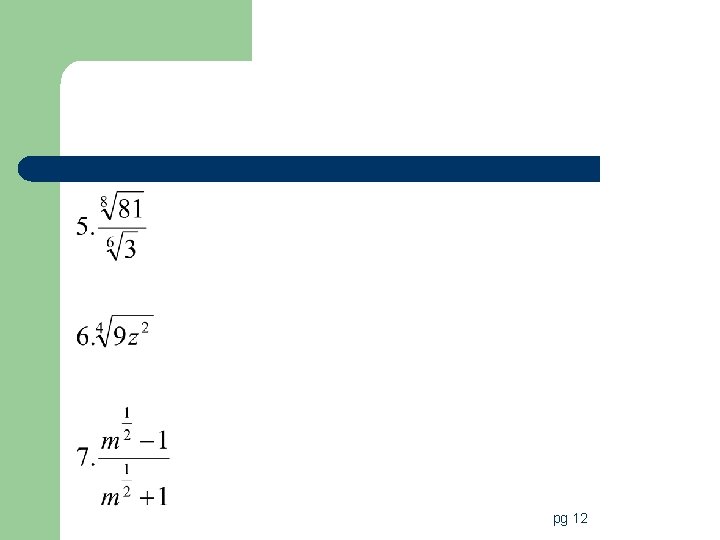





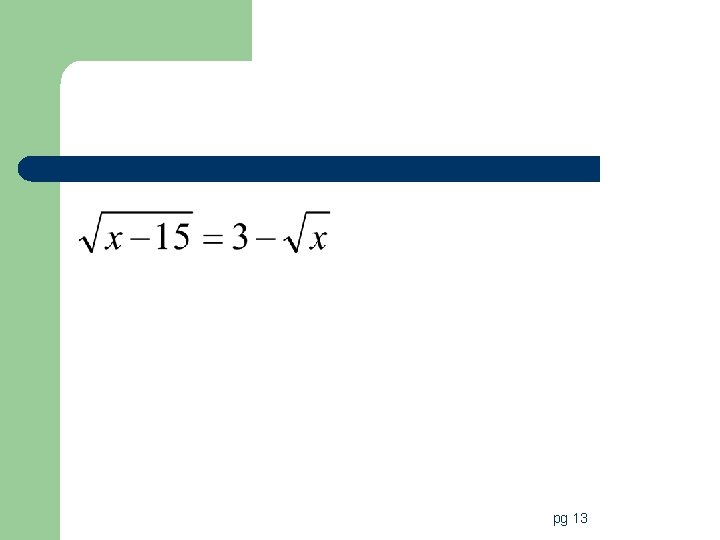
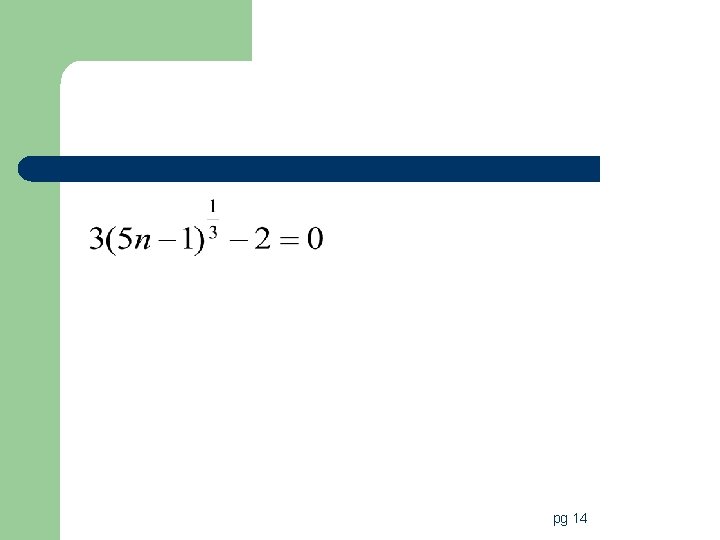
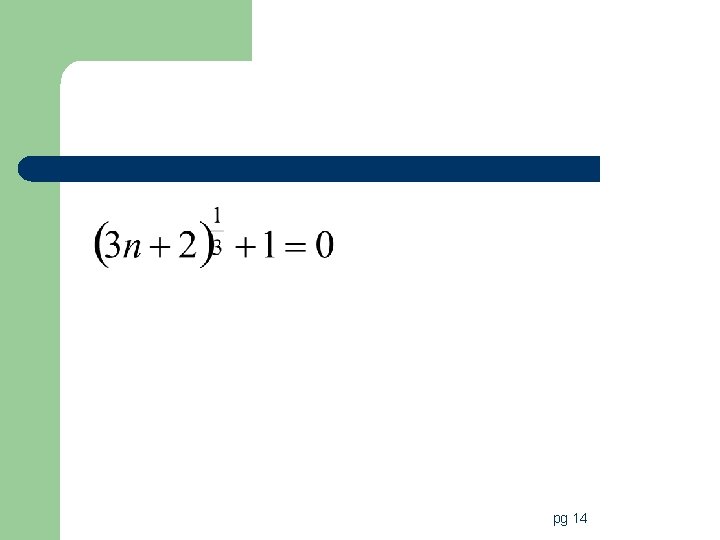

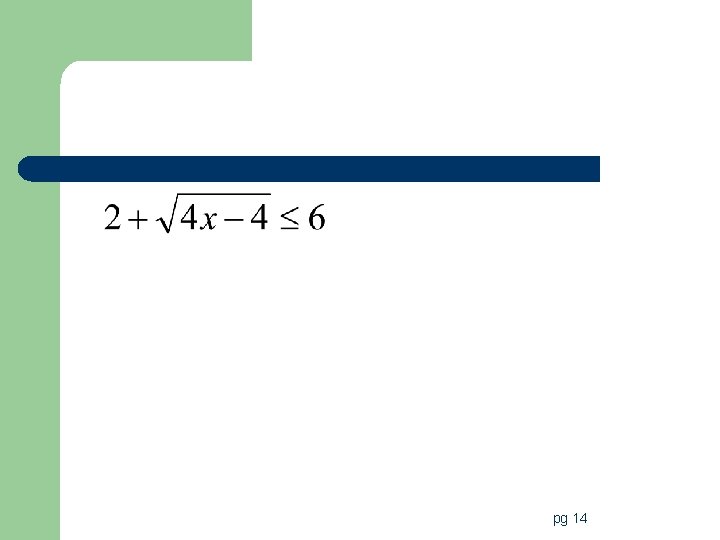
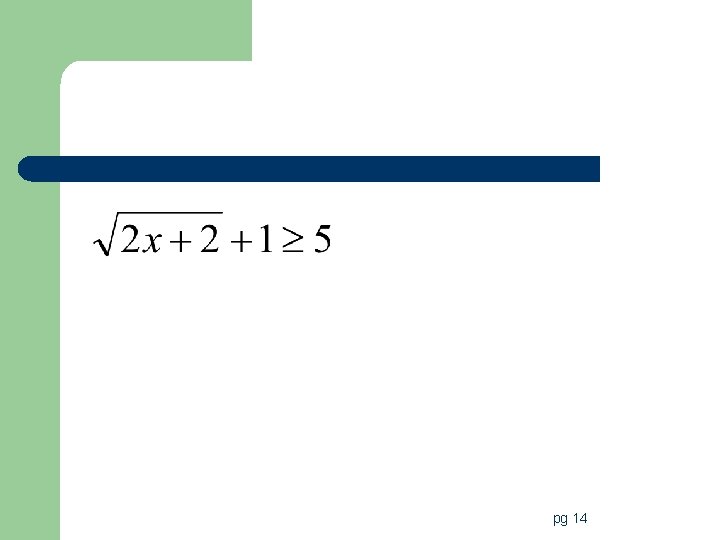
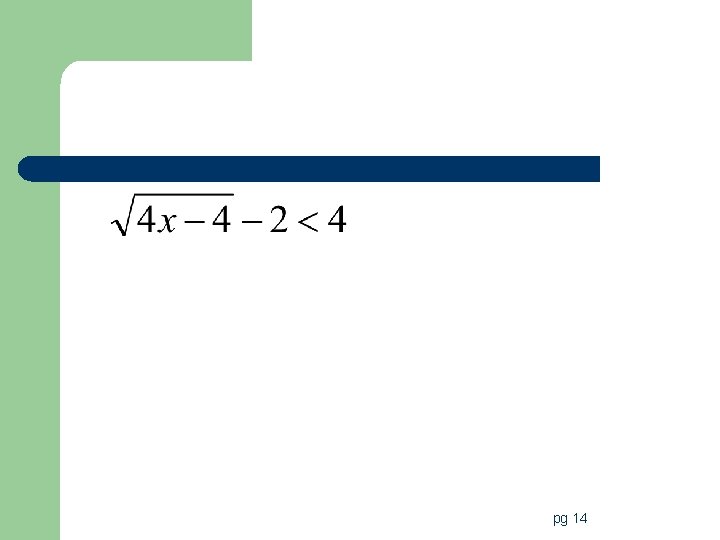
- Slides: 66

Chapter 7 Radical Equations

Lesson 7. 1 Operations of Functions

Operations with functions l (f + g)(x)= f(x) + g(x) l (f – g )(x) = f(x) – g(x) l (f · g)(x) = f(x) · g(x) l (f/g)(x) = f(x) , g(x) = 0 g(x) pg 1

Examples 1. f(x)= x 2 – 3 x + 1 and g(x) = 4 x + 5 find a. (f + g)(x) b. (f – g)(x) pg 1

2. f(x) = x 2 + 5 x – 2 and g(x) = 3 x -2 find a. (f + g)(x) b. (f – g)(x) pg 1

3. f(x) = x 2 + 5 x – 1 and g(x) = 3 x – 2 find a. (f · g)(x) b. (f/g)(x) pg 1
 = f[g(x)] – Plug in the full](https://slidetodoc.com/presentation_image_h/3222cbdff31555a196d767582cfc8f67/image-7.jpg)
Composition of Functions l [f o g](x) = f[g(x)] – Plug in the full function of g for x in function f pg 1
 and [g o f](x) for f(x) = x+3](https://slidetodoc.com/presentation_image_h/3222cbdff31555a196d767582cfc8f67/image-8.jpg)
Examples l Find [f o g](x) and [g o f](x) for f(x) = x+3 and g(x) = x 2 + x – 1 l Evaluate [f o g](x) for x = 2 and [g o f](x) pg 1

TOD: Find the sum, difference, product and quotient of f(x) and g(x) 1. f(x) = x 2 + 3 g(x) = x – 4 Find [g o h](x) and [h o g](x) 2. g(x) = 2 x 3. h(x) = 3 x – 4 If f(x) = 3 x, g(x) = x + 7 and h(x) = x 2 find the following 4. f[g(3)] 5. g[h(-2)] 6. h[h(1)]

Lesson 7. 2 Inverse Functions and Relations

Inverse Relations l Two relations are inverse relations if and only if one relation contains the element (a, b) the other relation contains the element (b, a) – Example: Q and S are inverse relations Q = {(1, 2), (3, 4), (5, 6)} S = {(2, 1), (4, 3), (6, 5)} pg 2

Examples 1. Find the inverse relation of {(2, 1), (5, 1), (2, -4)} 2. Find the inverse relation of {(-8, -3), (-8, -6), (-3, -6)} pg 2

Property of Inverse Functions l Suppose f and f-1 are inverse functions. Then f(a) = b if and only if f -1 (b) = a v. To find the inverse of a function: 1. Replace f(x) with y 2. Switch x and y 3. Solve for y 4. Replace y with f-1(x) 5. Graph f(x) and f-1(x) on the same coordinate plane pg 2

To Graph a function and it’s inverse 1. Make an x/y chart for f(x) then graph the points and connect the dots 2. Make an x/y chart for f-1(x) by switching the x and y coordinates and then graph and connect the dots - The graphs should be reflections of one another over the line y=x pg 2

Examples l Find the inverse of and then graph the function and its inverse pg 3

l Find the inverse of and then graph the function and its inverse f(x) = 2 x - 3 pg 3

Inverse Functions l Two functions f and g are inverse functions if and only if both of their compositions are the identity function. [f o g](x) = x and [g o f](x) = x pg 3

Determine if the functions are inverses pg 3

Determine if the functions are inverses pg 3

Lesson 7. 3 Square Root Functions and Inequalities

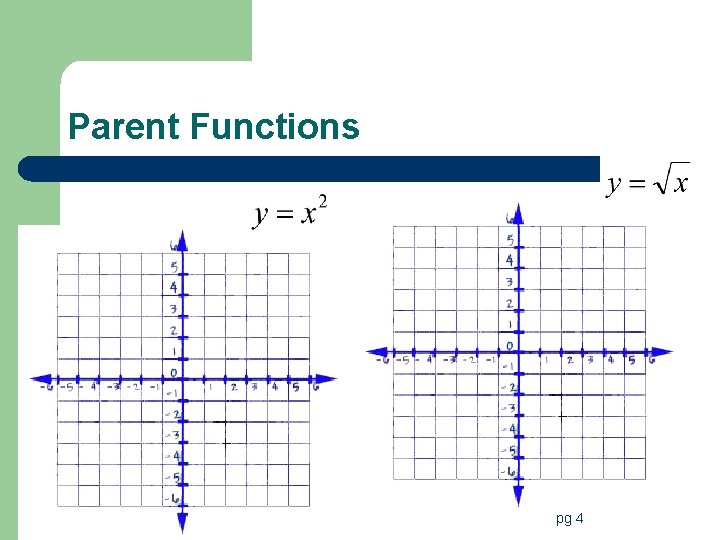
Square Root Functions l Definition: when a function contains a square root of a variable l The inverse of a quadratic function (starts with x 2) is a square root function only if the range has no negative numbers!! pg 4

Parent Functions pg 4

Graphing Square Root Functions 1. Find the domain. The radicand (the stuff inside the square root) cannot be negative so take whatever is inside and make it greater than or equal to 0 and solve. 2. Plug the x value you found back in and solve for y. 3. Make a table starting with the ordered pair you found in steps 1 & 2. Graph. 4. State the range. pg 4

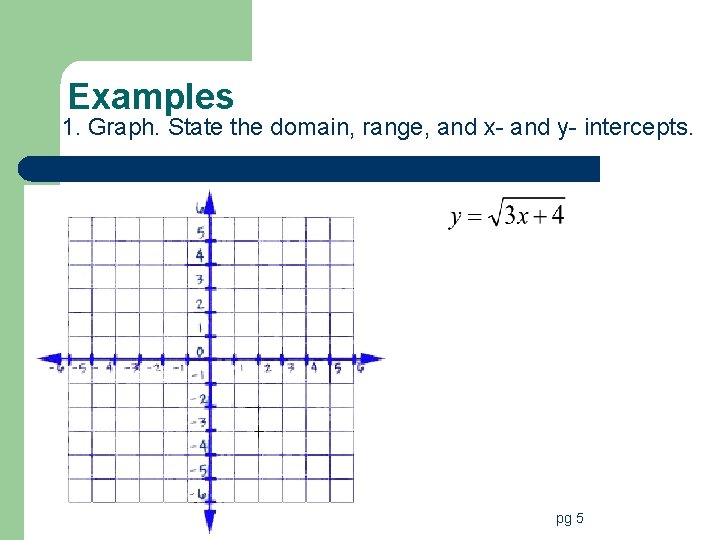
Examples 1. Graph. State the domain, range, and x- and y- intercepts. pg 5

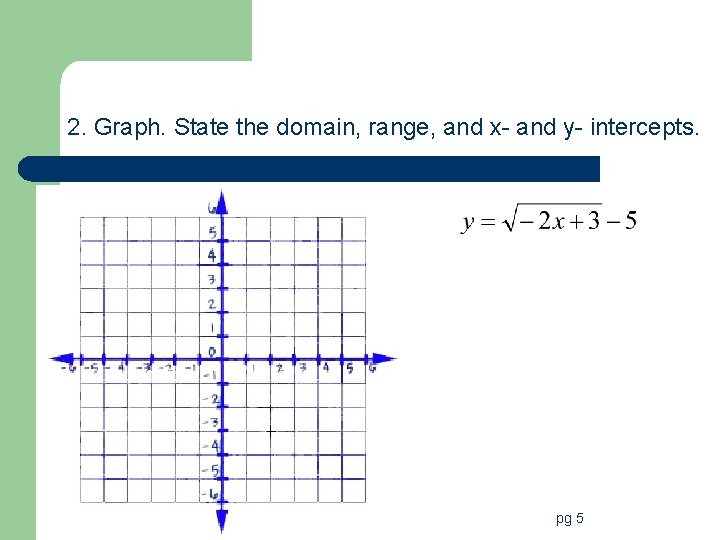
2. Graph. State the domain, range, and x- and y- intercepts. pg 5

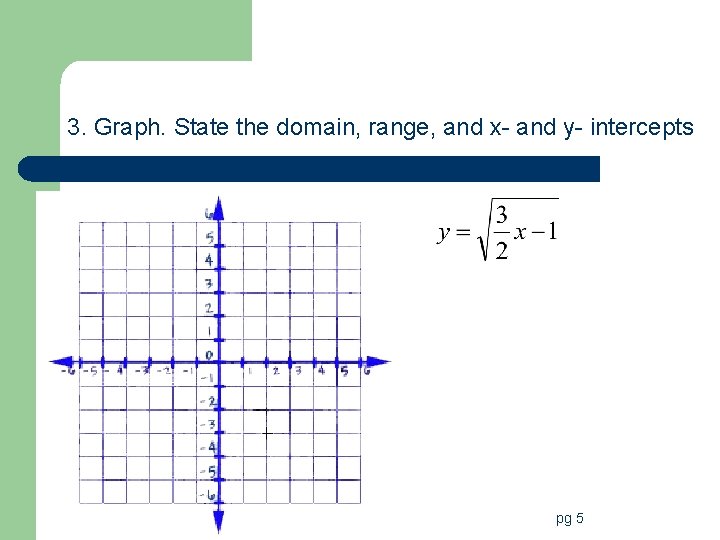
3. Graph. State the domain, range, and x- and y- intercepts pg 5

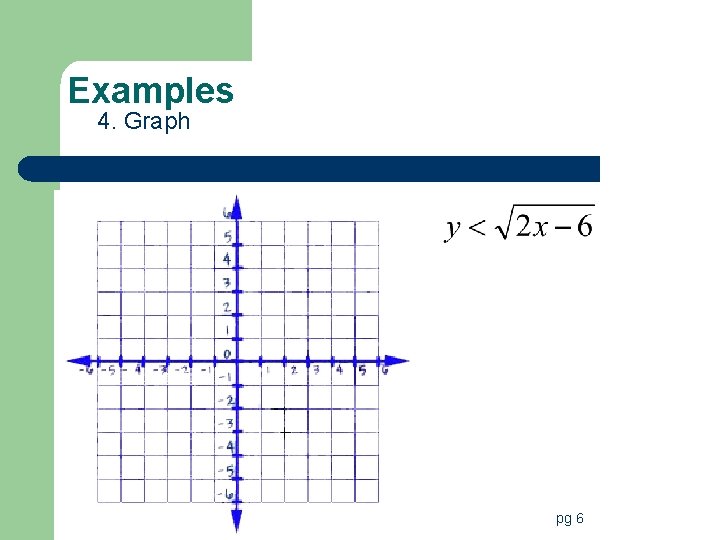
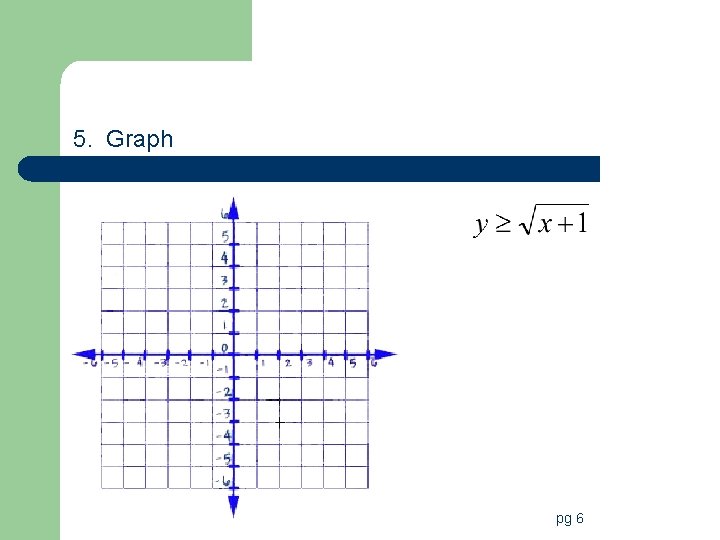
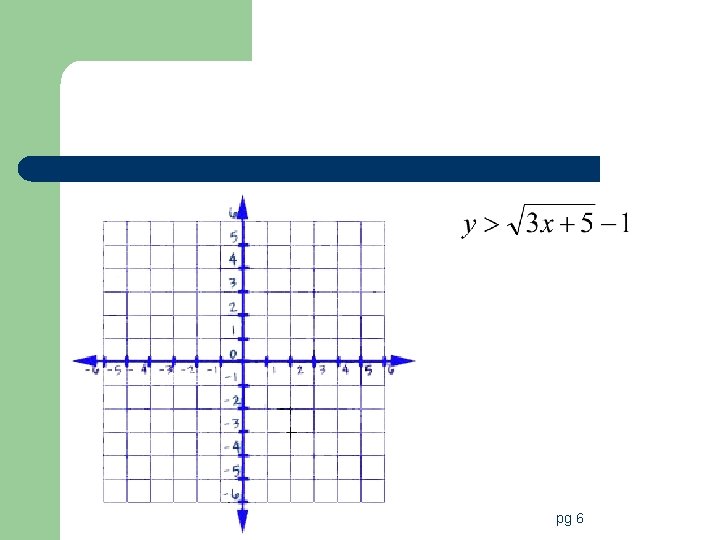
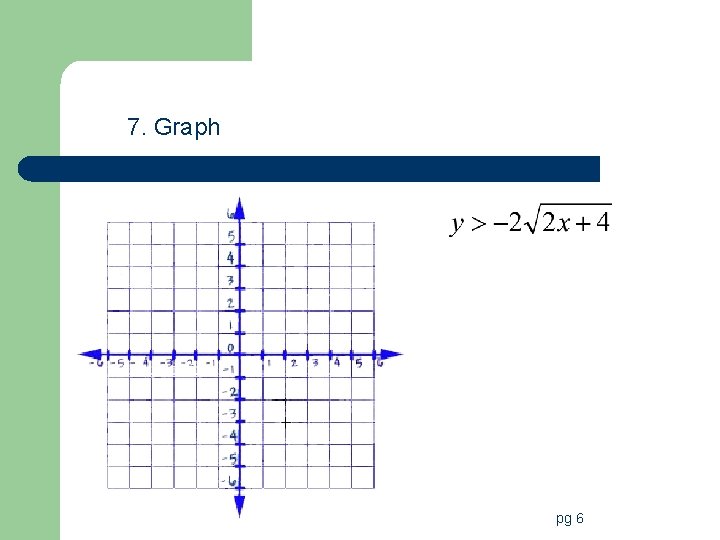
Square Root Inequalities l Follow same steps as an equation to graph but add last step of shading. l Remember rules for solid and dotted lines!! pg 6

Examples 4. Graph pg 6

5. Graph pg 6

6. Graph pg 6

7. Graph pg 6

7. 4 Nth Roots

Nth Roots pg 7

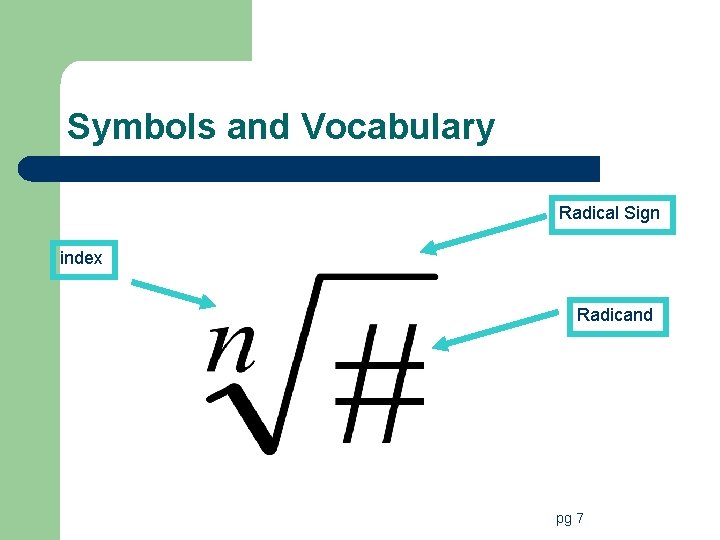
Symbols and Vocabulary Radical Sign index Radicand pg 7

More Vocabulary l Principal Root: the nonnegative root – Example: 36 has two square roots, 6 and -6 – 6 is the principal root because it is positive Other things to remember: - If the radical sign has a – in front of it this indicates the opposite of the principal square root - If the radical has a ± in front of it then you give both the principal and the opposite principal roots pg 7

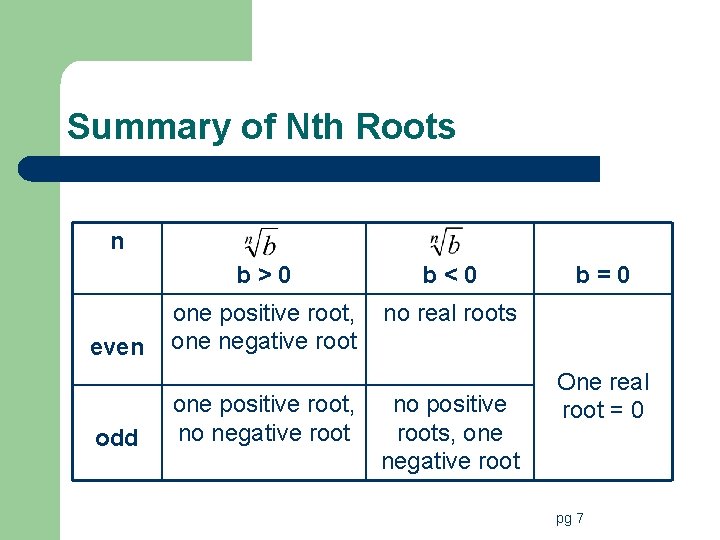
Summary of Nth Roots n even odd b>0 b<0 one positive root, one negative root no real roots one positive root, no negative root no positive roots, one negative root b=0 One real root = 0 pg 7

Examples pg 8

Your turn… pg 8

More things to remember… l When you find the nth root of an even power and the result is an odd power, you must take the absolute value of the result to ensure that the answer is nonnegative – pg 8

Examples Using Absolute Values pg 8

7. 5 Operations with Radical Expressions

Review of Properties of Radicals Product Property Quotient Property If all parts of the radicand are positive - separate each part so that it has the nth root Ex: pg 9

When is a radical simplified? -The nth root is as small as possible -The radicand has no fractions -There are no radicals in the denominator pg 9

Rationalizing the Denominator l If you have a fraction with a radical in the denominator you must rationalize the denominator, multiply the numerator and denominator by the square root in the denominator. pg 9

Examples pg 9
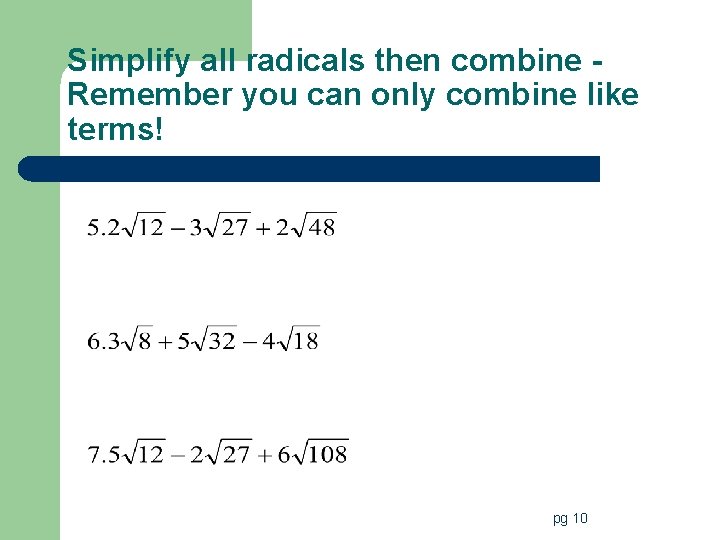
Simplify all radicals then combine Remember you can only combine like terms! pg 10

Foil- then simplify pg 10

Multiply by the conjugate- then simplify pg 10

7. 6 Rational Exponents

Fractions, are our Friends! l What do we do when we have a fraction as an exponent? – Change it into a radical v The denominator of becomes the index of the radical The numerator becomes the power for the radicand v v Ex: = pg 11

Examples pg 11

Generalization for numerator greater than 1 If the numerator is bigger than 1: v. The denominator becomes the index for the radical (nth root) v. The numerator becomes the power for the nth root of the radicand v. Ex: = = pg 11

Examples pg 12
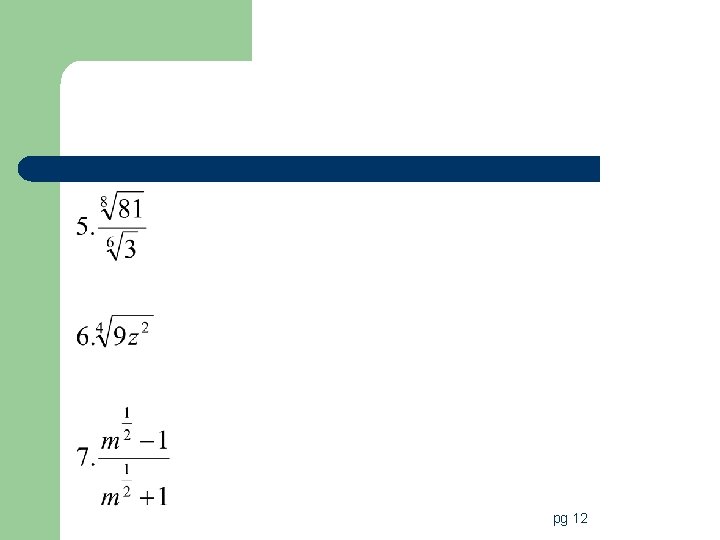
pg 12

pg 12

7. 7 Solving Radical Equations and Inequalities

Vocabulary l Radical equations/inequalities: equations/inequalities that have variables in the radicands l Extraneous Solution: when you get a solution that does not satisfy the original equation. pg 13

Steps to solve radical equations/inequalities 1. Isolate the radical. – If there is more than one, isolate the radical that has the most stuff in it first! 2. Raise both sides to the power that will eliminate the radical. – If there is more than one radical you will have to repeat this step until there are no more radicals in the problem 3. Solve for the variable. 4. Test solutions to check for extraneous roots. pg 13

Solve Radical Equations pg 13
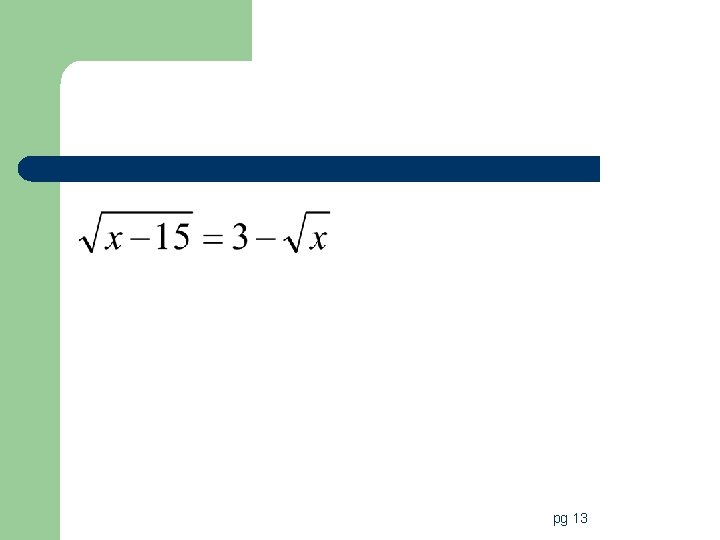
pg 13
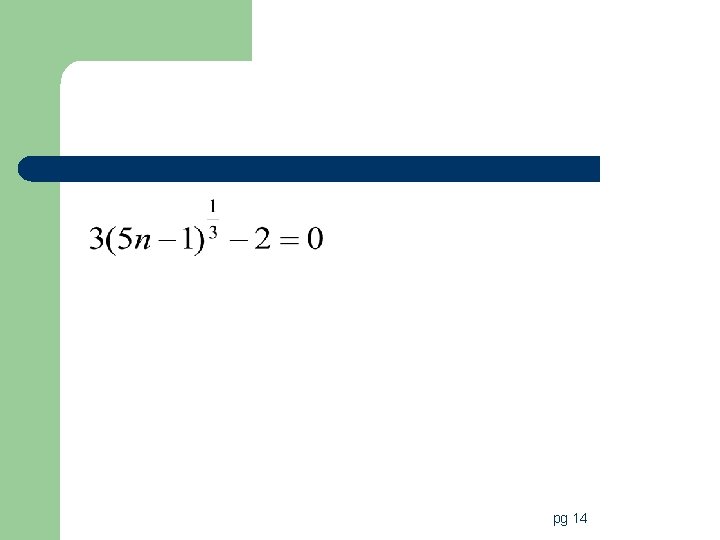
pg 14
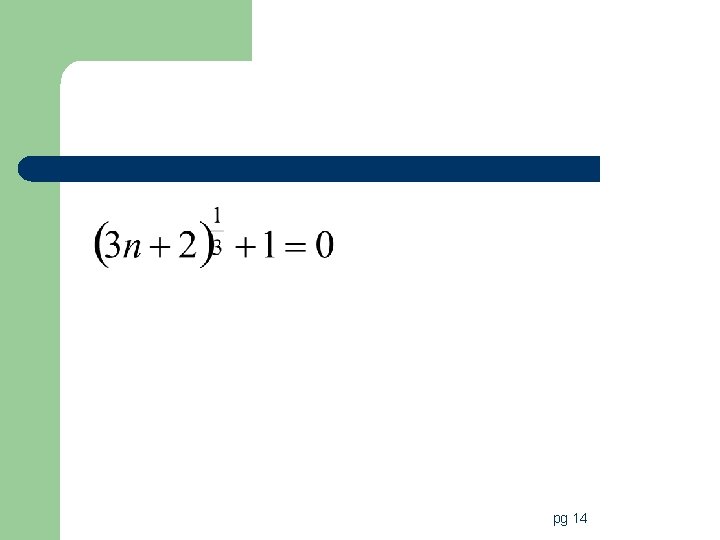
pg 14

Day #2 Now let’s look at inequalities l Steps to Solve a radical inequality 1. Identify the values of x for which the root is defined. 2. Solve given inequality by isolating and then eliminating the radical 3. Test values to confirm your solution (use a table to do this) 4. Graph solution on a number line. (Remember open and closed dots) pg 14
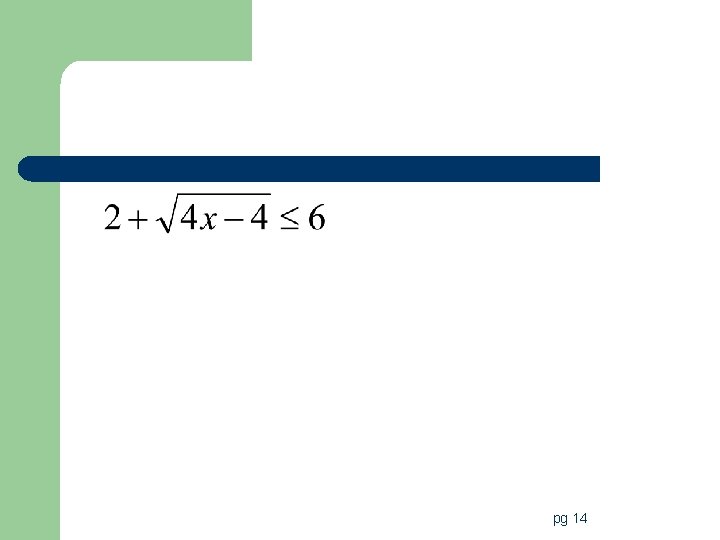
pg 14
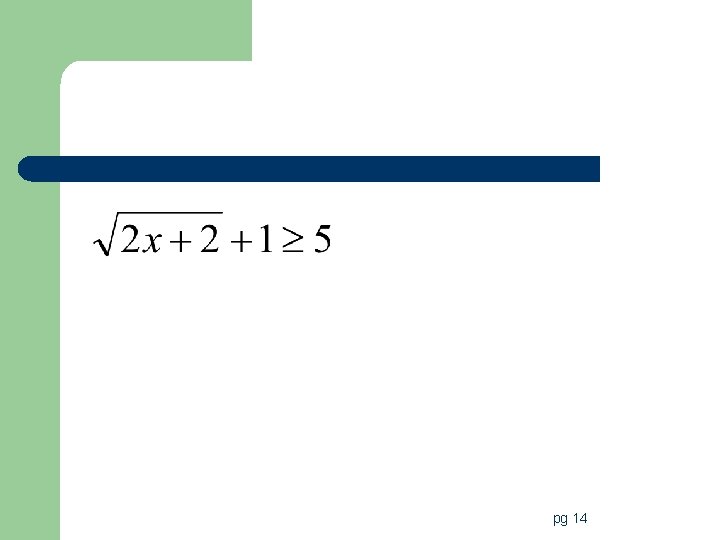
pg 14
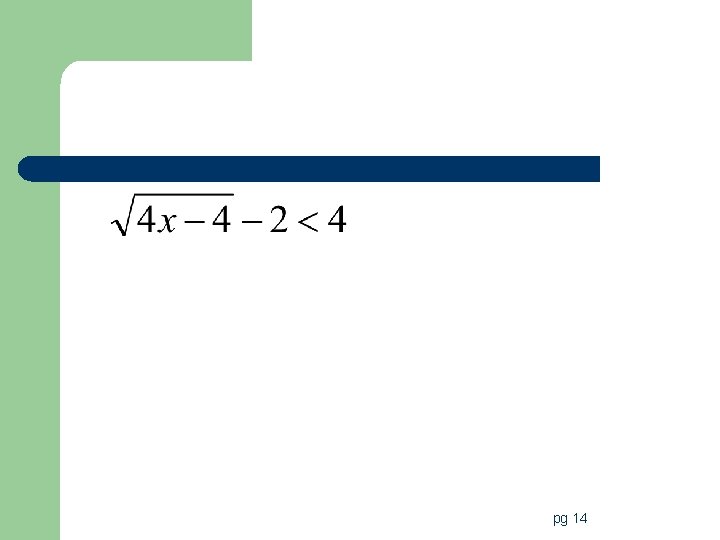
pg 14