Unit 6 RATIONAL EXPONENTS AND RADICAL FUNCTIONS Unit













































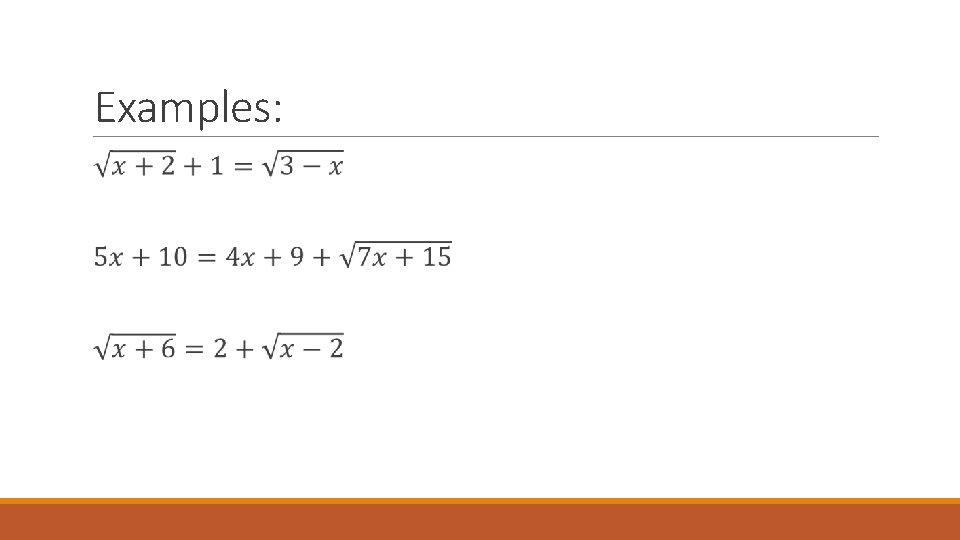


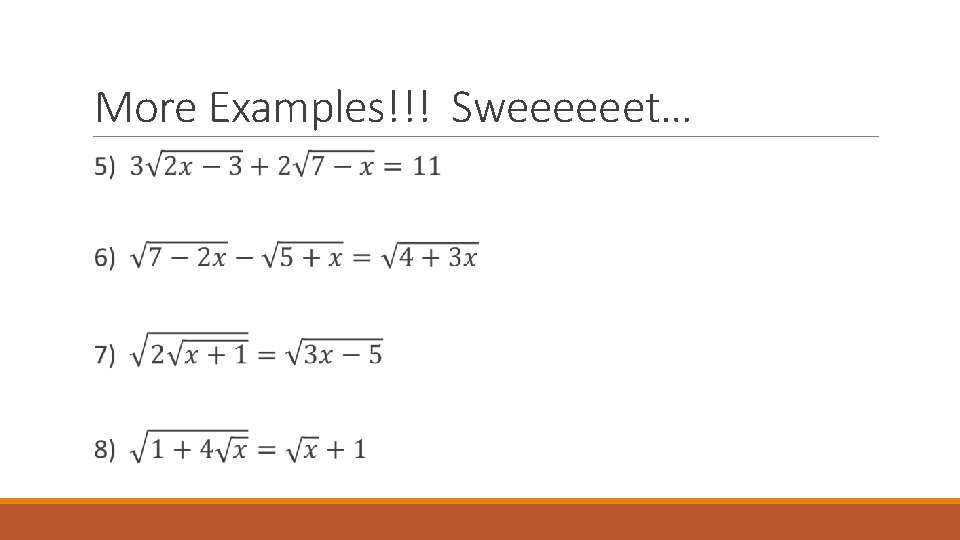



- Slides: 52

Unit 6 RATIONAL EXPONENTS AND RADICAL FUNCTIONS

Unit Essential Question: What are the different properties of exponents and radicals that allow us to solve equations?

Lesson 6. 1 RATIONAL EXPONENTS AND NTH ROOTS

Lesson Essential Question: How are nth roots and rational exponents related and how can they be used to simplify expressions?

Nth Roots

Nth Roots

Rational Exponents: How can we rewrite nth roots as exponents? How can we rewrite exponents as nth roots?

Homework: Pages 417 -418 #’s 3 – 49 odds

Bell Work:

Examples:

Examples:

Lesson 6. 2 APPLY PROPERTIES OF RATIONAL EXPONENTS

Lesson Essential Question: What are the different properties of rational exponents and how are they used to simplify expressions?

Properties of Rational Exponents: Blue Tables on Pages 420 – 421

Examples:

Bell Work:

Homework: Pages 424 – 425 #’s 3 – 65 odds

Bell Work:

Class Work: Pages 424 – 425 #’s 4 – 54 evens This assignment will be collected!!! Small Quiz tomorrow at the beginning of class on Properties of Exponents and Radicals. (NO CALCULATORS!!!)

Bell Work:

Quiz:

Lesson 6. 3 OPERATIONS AND COMPOSITIONS OF FUNCTIONS

Lesson Essential Question: How do we perform operations on functions, and how do we take a composition of two or more functions?

Operations on Functions:

Domain: Remember that domain is the set of all x-values that will work for a given function. When we perform operations, this can sometimes alter the domain of the original functions. Lets look back at the four operations we did, and find the domain for each:

Compositions of Functions:

Notation:

Homework: Page 432 #’s 3 – 37 odds

Bell Work:

Classwork/Homework: This assignment will be collected tomorrow!!! Pages 432 – 433 #’s 4 – 38 evens

Bell Work:

Lesson 6. 4 INVERSE FUNCTIONS

Lesson Essential Question: How do we find an inverse function and how does it relate to its original function? ? ?

Inverse Functions: To prove that two functions are inverses, then the composition of the two functions must come out to be x. If f(x) and g(x) are inverses, then f(g(x)) = x and g(f(x)) = x.

Graphs of Inverse Functions:

If two functions are inverses, then… 1) The composition of the functions will come out to be x. 2) They have reversed x and y values. (This means the domain and range are switched!) 3) The graphs of the functions are reflected about the line y = x.

Notation:

Bell Work:

Steps for finding an inverse function…

Homework: Pages 442 – 443 #’s 3 – 27 odds

Bell Work:

Lesson 6. 6 SOLVING RADICAL EQUATIONS

Lesson Essential Question: How do we solve radical equations and why is it important to check our solutions?

Steps for solving a radical equation: 1) Isolate one of the radicals 2) Raise both sides to a power to cancel out the isolated radical. 3) Repeat steps 1 and 2 if necessary. 4) Solve. 5) Check for extraneous solutions!

Examples:
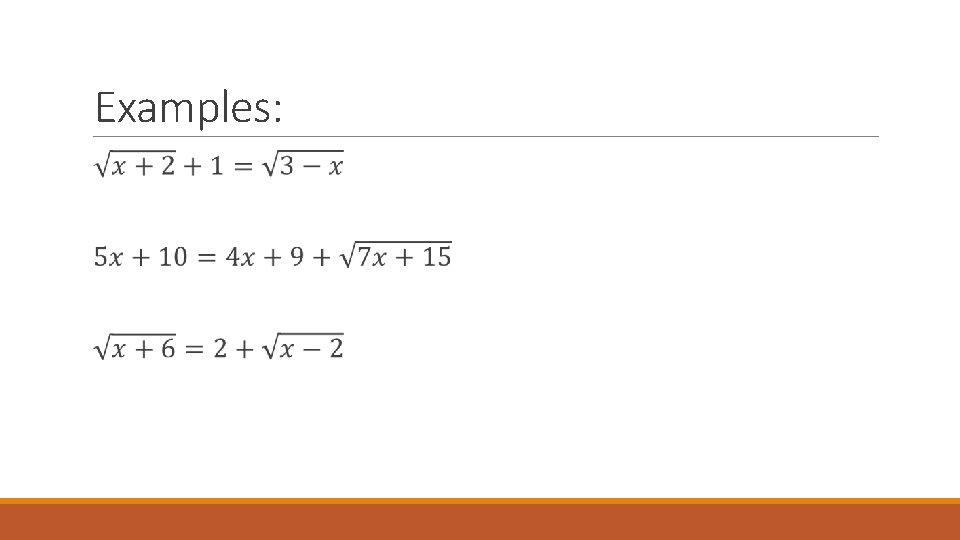
Examples:

Homework: Pages 456 – 457 #’s 3 – 21 odds and 35 – 51 odds

Bell Work:
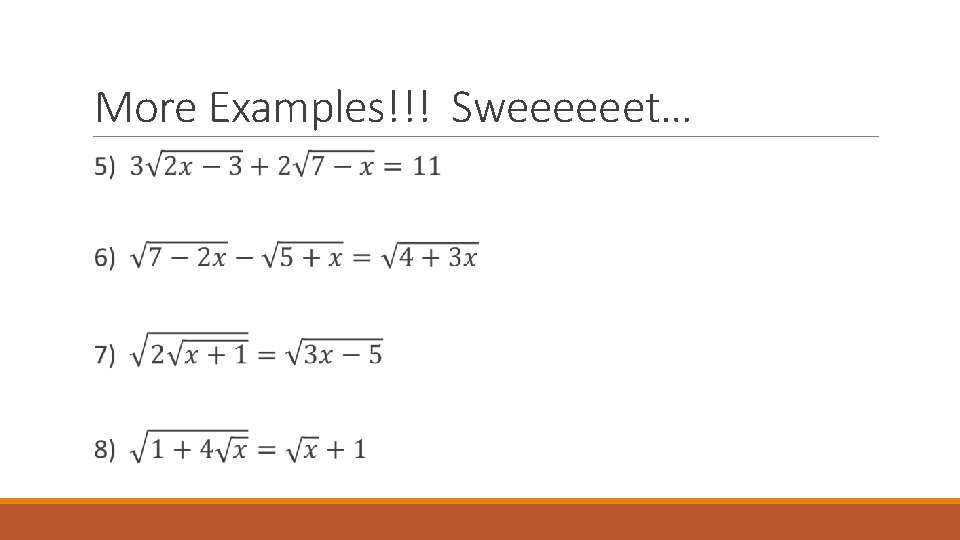
More Examples!!! Sweeeeeet…

Homework: This assignment will be collected!!! Pages 456 – 457 #’s 4, 10, 16, 20, 24, 28, 38, 50, 52

Bell Work:

Unit 6 Test Upcoming!!!!!!!!!!!! Properties of Radicals Properties of Exponents Operations and Compositions of Functions Inverse Functions Solving Radical Equations
 Quiz 6-1 radicals and rational exponents answers
Quiz 6-1 radicals and rational exponents answers Unit 6 test radical functions
Unit 6 test radical functions Unit 6 radical functions homework 4 rational exponents
Unit 6 radical functions homework 4 rational exponents Exponents algebra 2
Exponents algebra 2 Rational exponents
Rational exponents Exponent warm up
Exponent warm up 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents 5-6 radical expressions and rational exponents
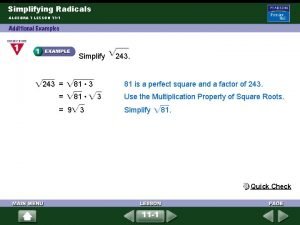
5-6 radical expressions and rational exponents Simplify square root of 384
Simplify square root of 384 Unit 6 radical functions homework 3
Unit 6 radical functions homework 3 Exponents in fractions
Exponents in fractions Rewrite without an exponent
Rewrite without an exponent Fractions in exponents
Fractions in exponents Radicals and complex numbers
Radicals and complex numbers Solving equations with radicals and rational exponents
Solving equations with radicals and rational exponents Entire to mixed radical
Entire to mixed radical Radical section
Radical section Function operations multiplication
Function operations multiplication Radical and rational expressions
Radical and rational expressions Properties of rational exponents
Properties of rational exponents Simplify rational exponents
Simplify rational exponents 6-2 rational exponents
6-2 rational exponents Distributing exponents to fractions
Distributing exponents to fractions Rational exponents
Rational exponents Evaluating nth roots
Evaluating nth roots More multiplication properties of exponents
More multiplication properties of exponents Horizontal asymptote rules
Horizontal asymptote rules Rational exponent to radical form calculator
Rational exponent to radical form calculator Unit 8 rational functions homework 1
Unit 8 rational functions homework 1 How to solve rational equations and inequalities
How to solve rational equations and inequalities Zyntax
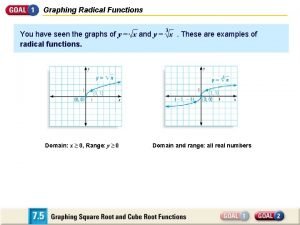
Zyntax Transformation of a square root function
Transformation of a square root function Biologists have discovered that the shoulder height h
Biologists have discovered that the shoulder height h Horizontal asymptote equation
Horizontal asymptote equation Rational expressions and functions
Rational expressions and functions Integration of irrational functions
Integration of irrational functions Rational functions holes and asymptotes
Rational functions holes and asymptotes Vertical answer
Vertical answer Chapter 4 polynomial and rational functions
Chapter 4 polynomial and rational functions Chapter 3 polynomial and rational functions
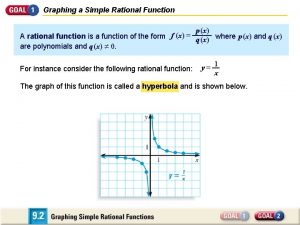
Chapter 3 polynomial and rational functions Rational functions and their graphs
Rational functions and their graphs Rational function properties
Rational function properties Horizontal asymptote
Horizontal asymptote Lesson 3: rational functions and their graphs
Lesson 3: rational functions and their graphs Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Rational function parent function
Rational function parent function Transforming rational functions
Transforming rational functions What are the properties of rational function?
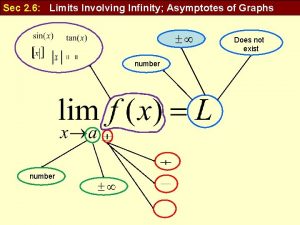
What are the properties of rational function? Sec infinity
Sec infinity What is rational function
What is rational function Rational function examples
Rational function examples Rational function vertex form
Rational function vertex form Rational function graph in real life
Rational function graph in real life