Unit 8 Radical Rational Functions LG 8 1











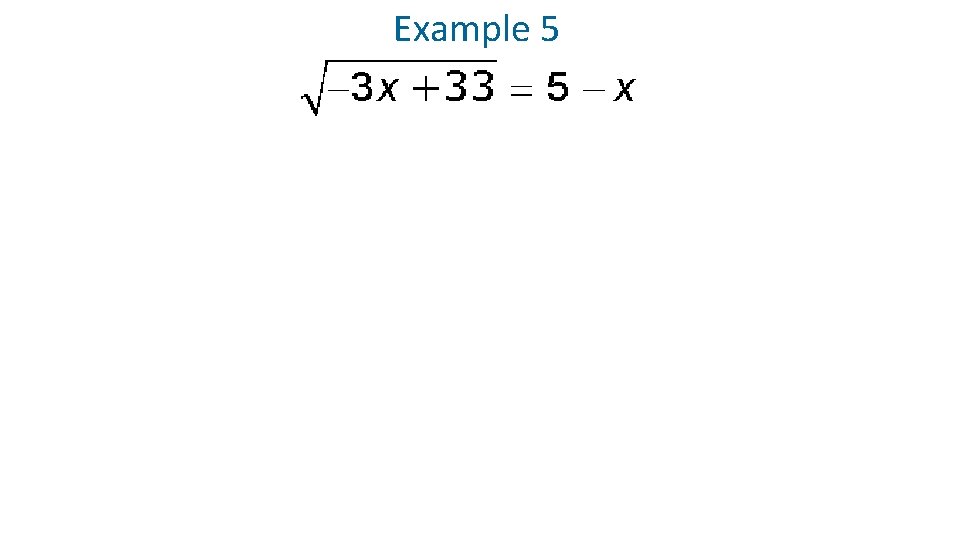

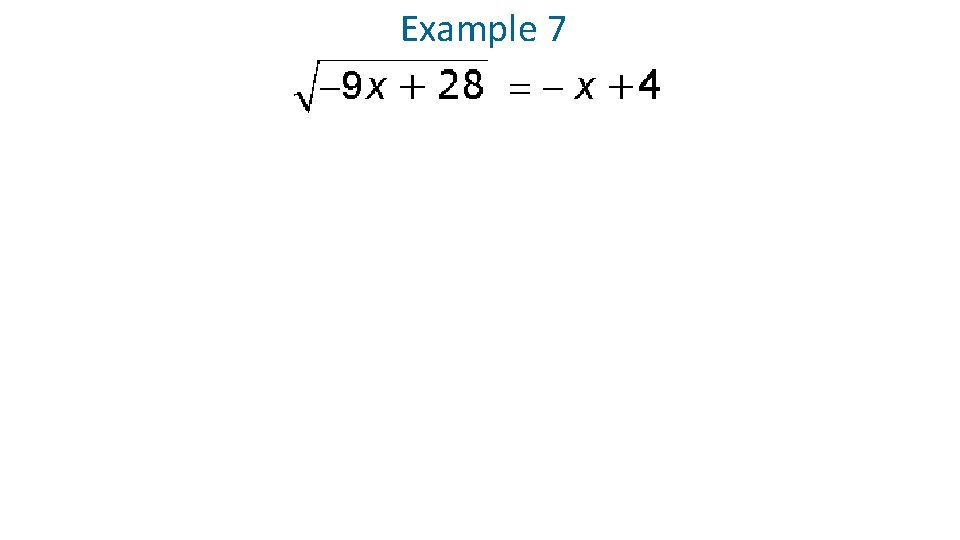


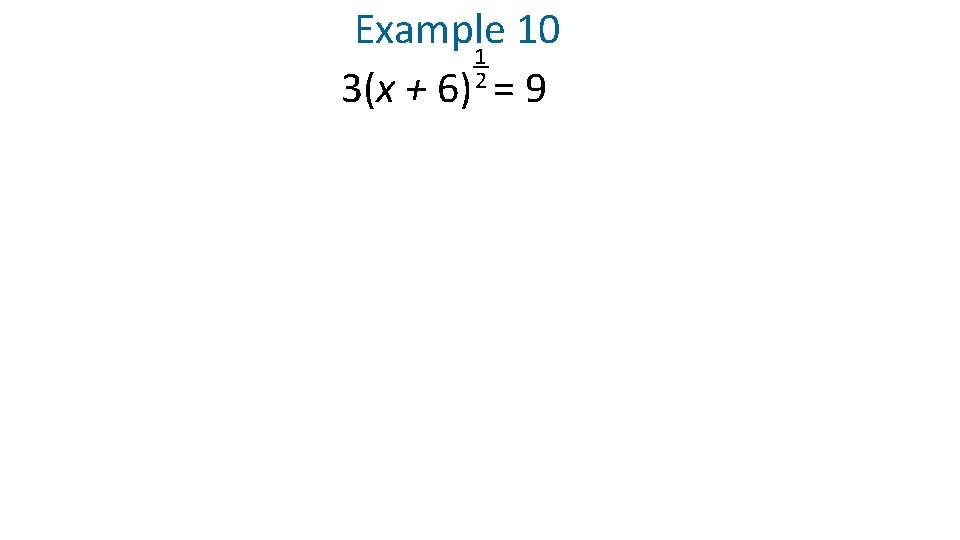




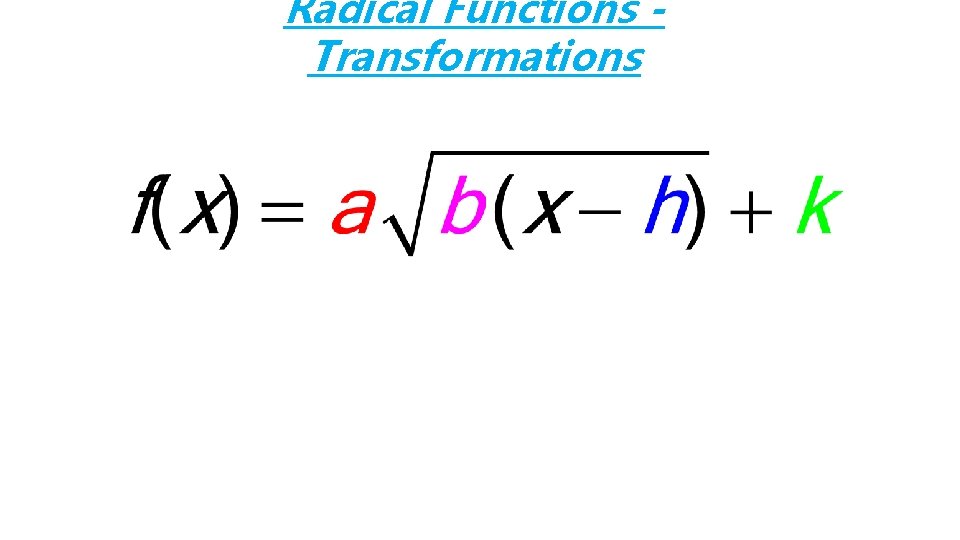



































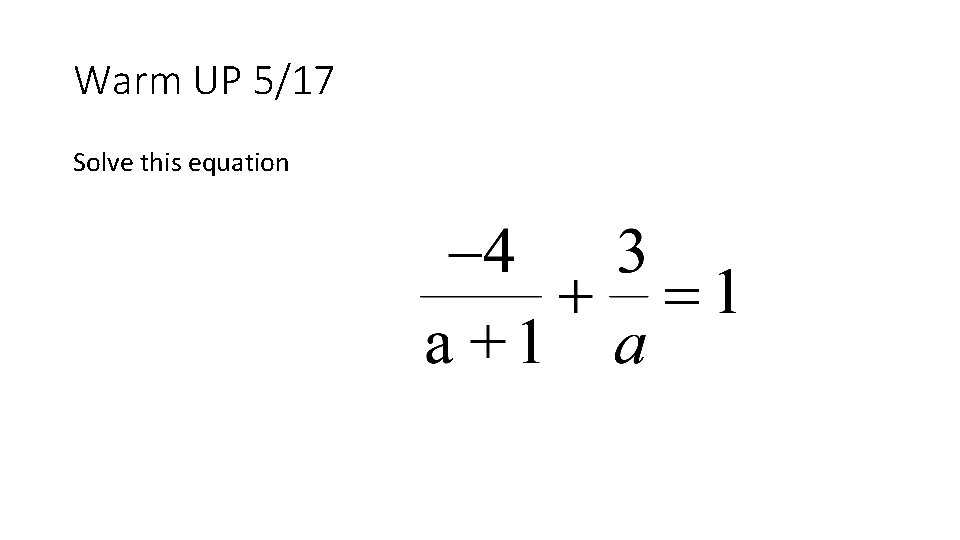
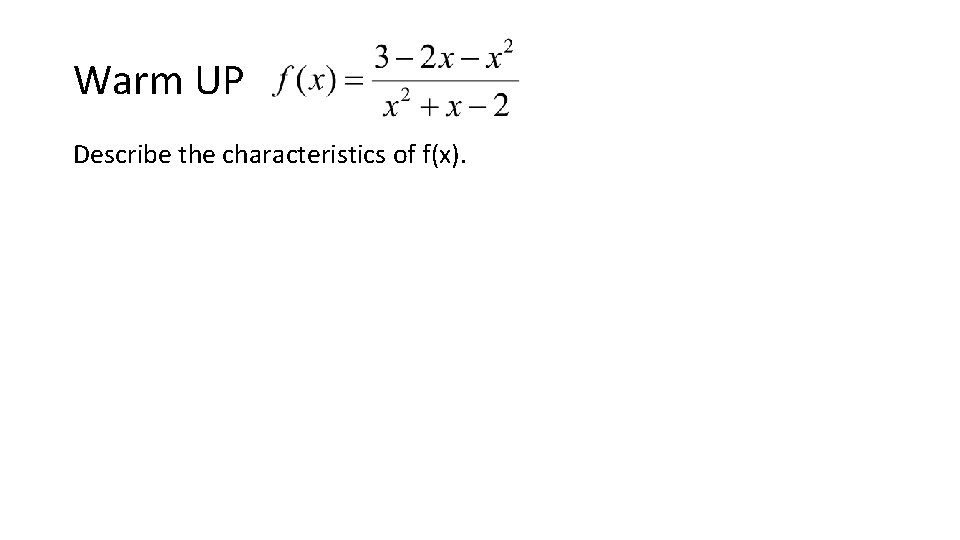


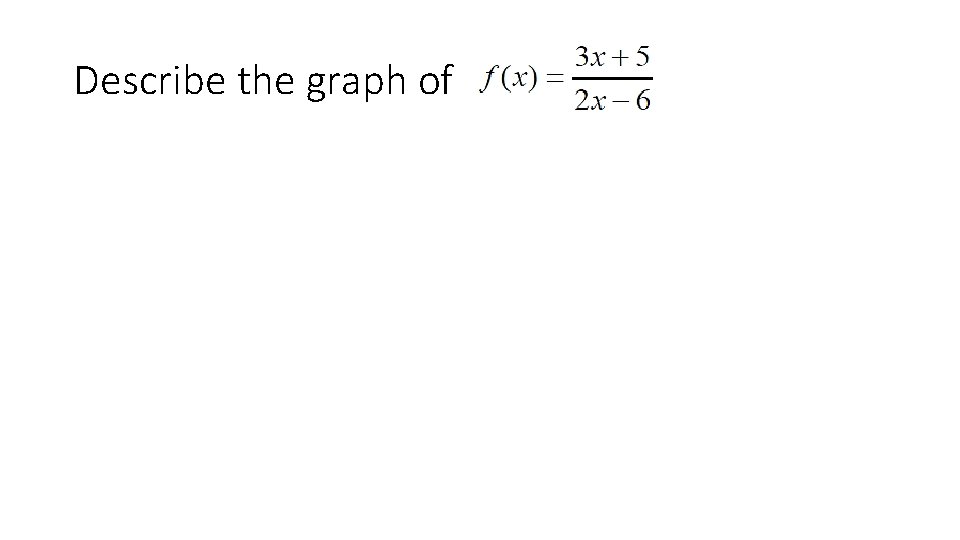
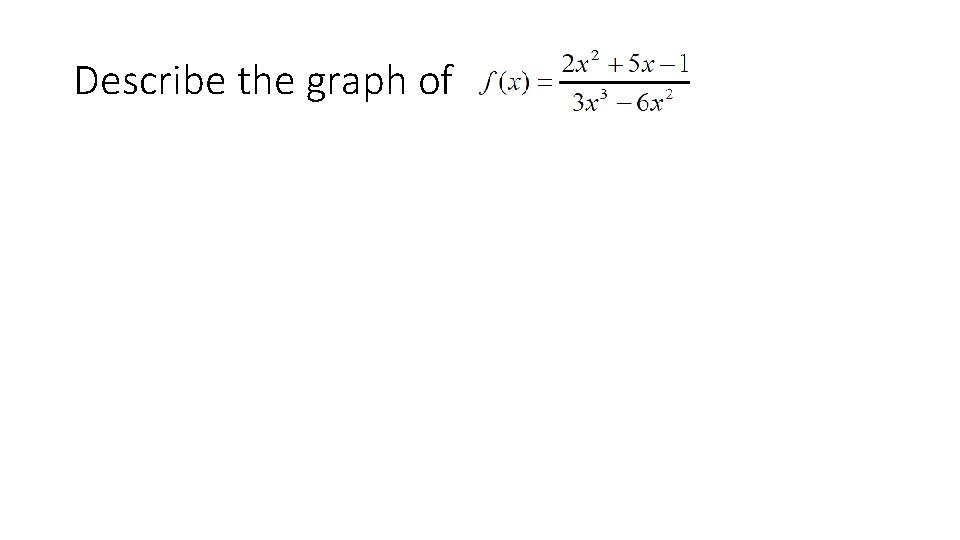
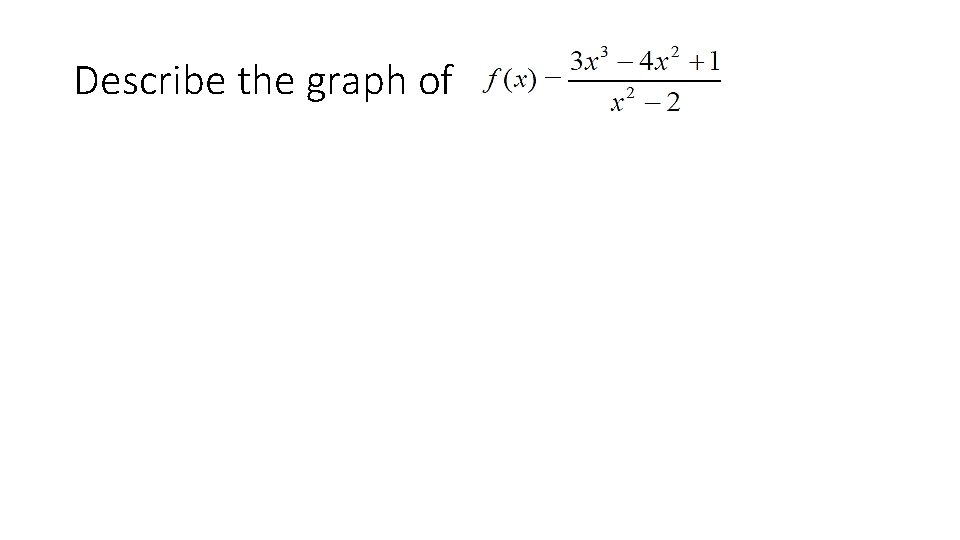





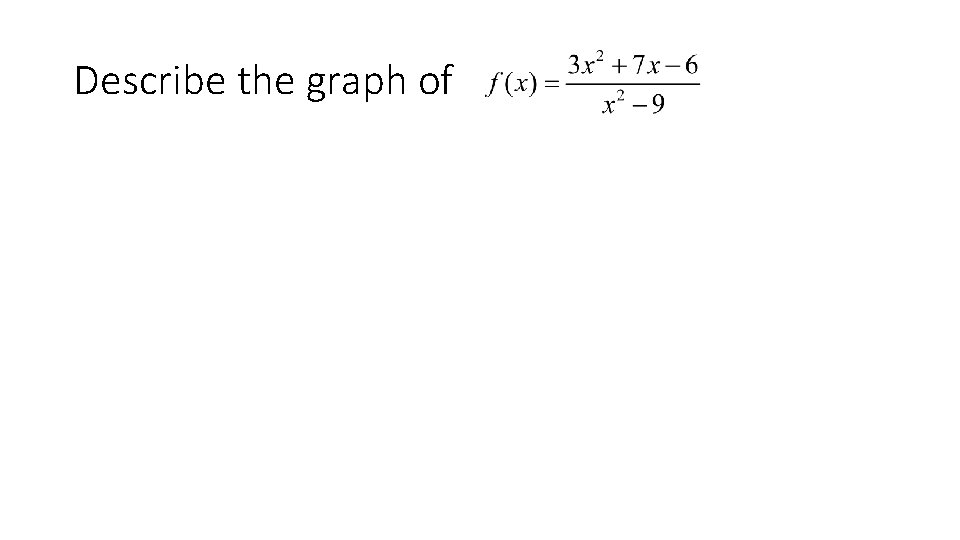
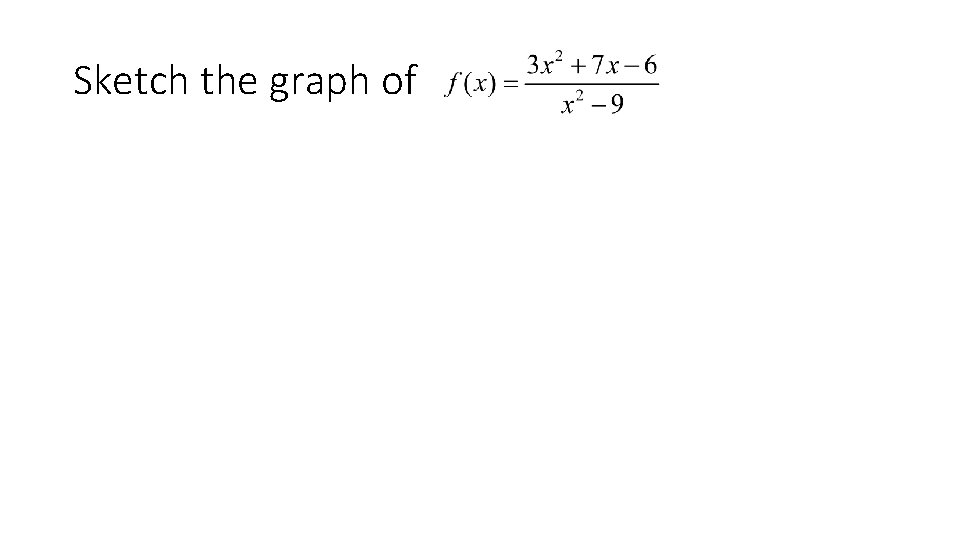


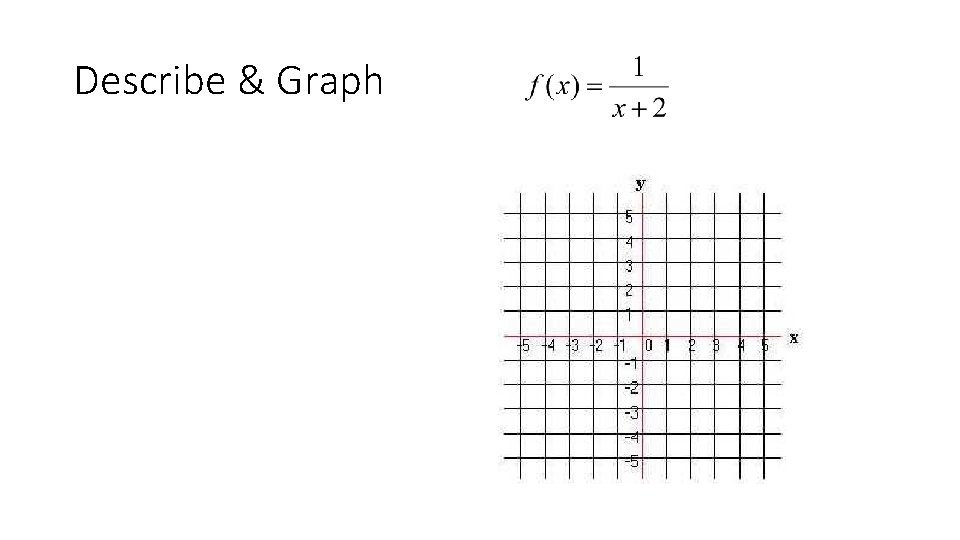
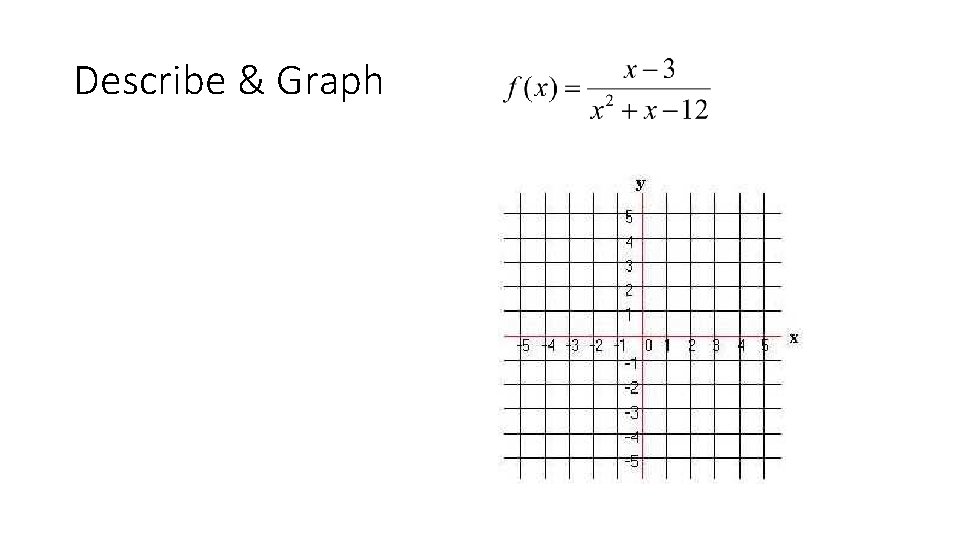
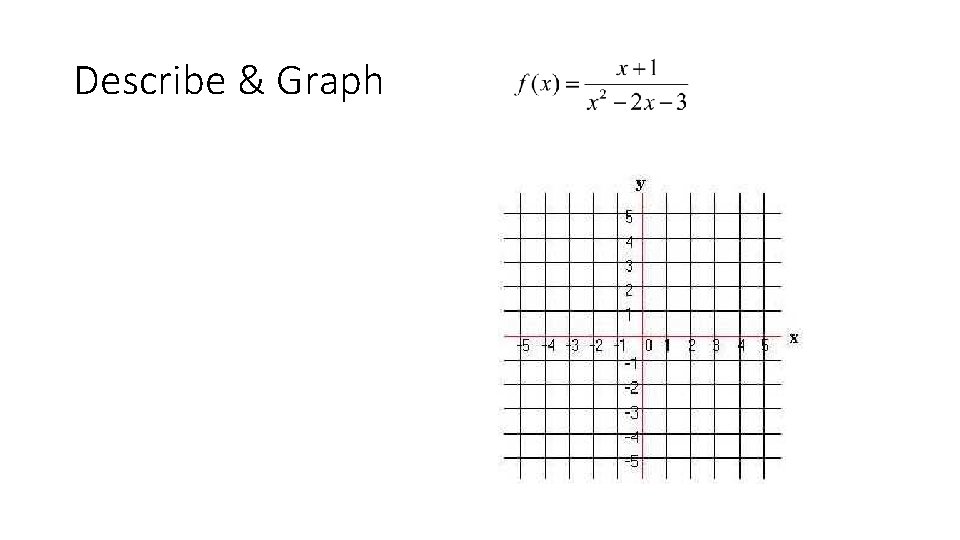
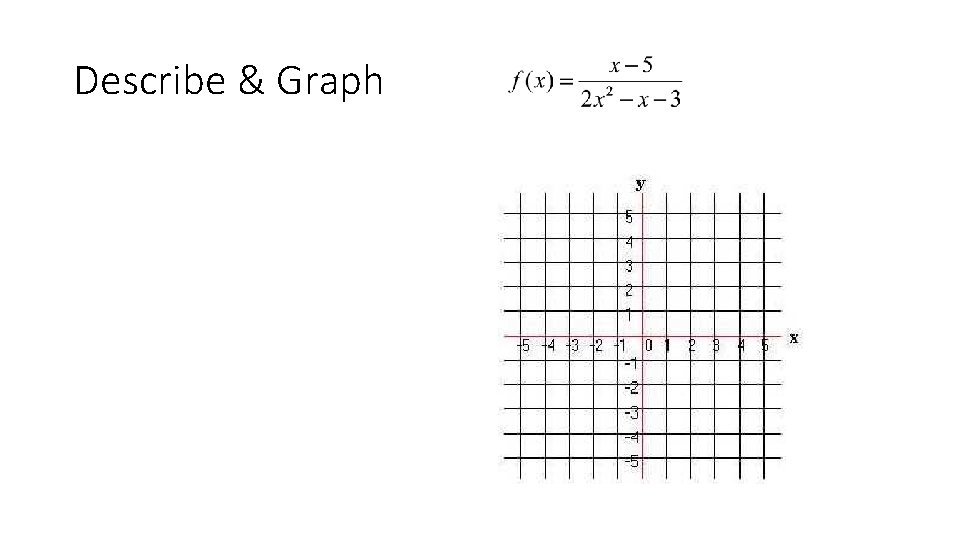




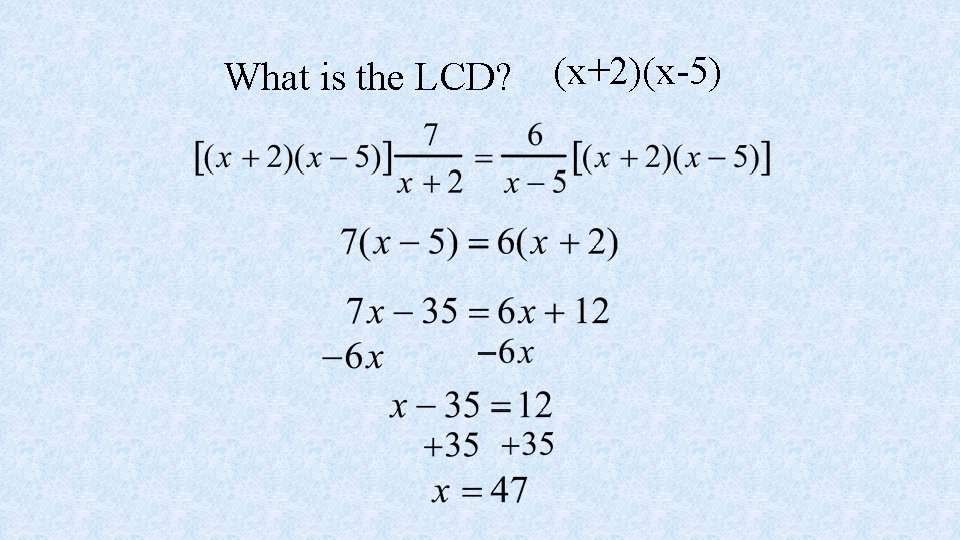


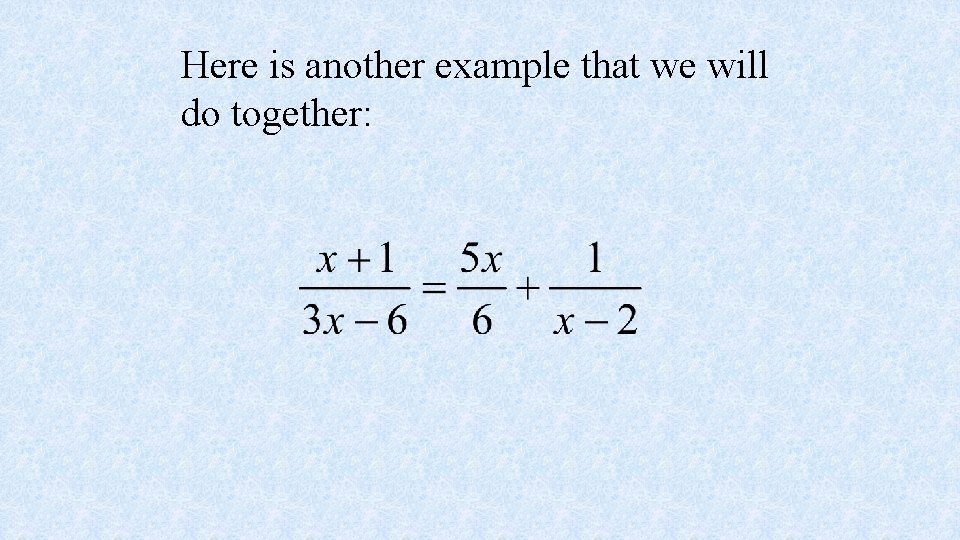

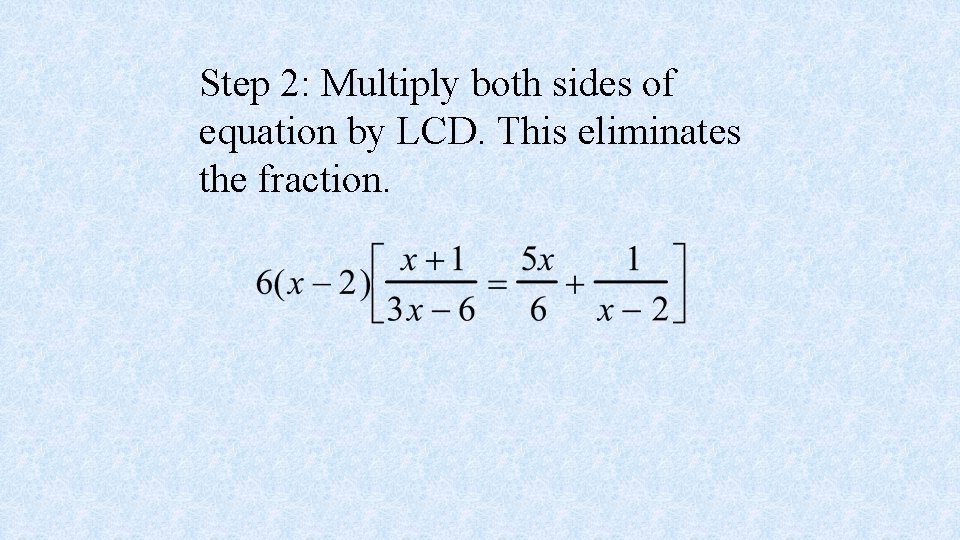
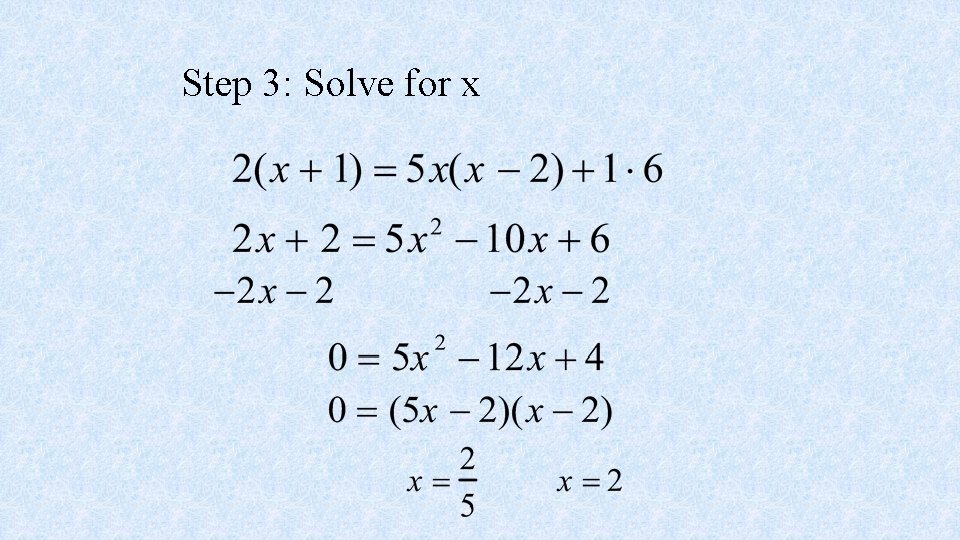


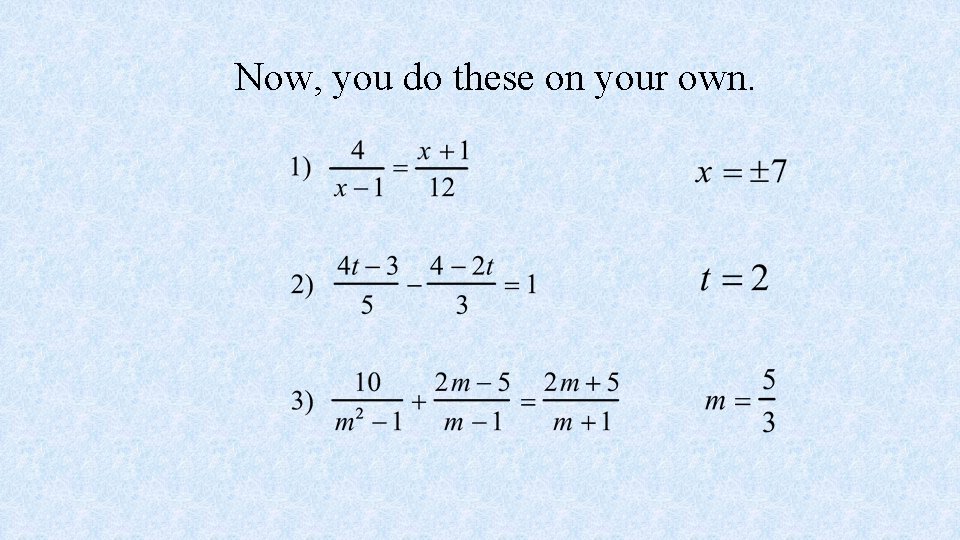



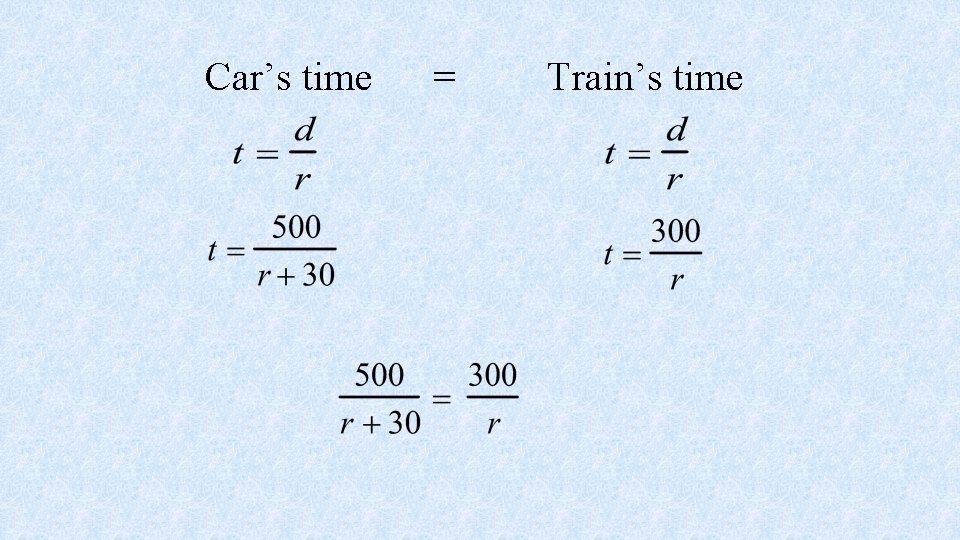
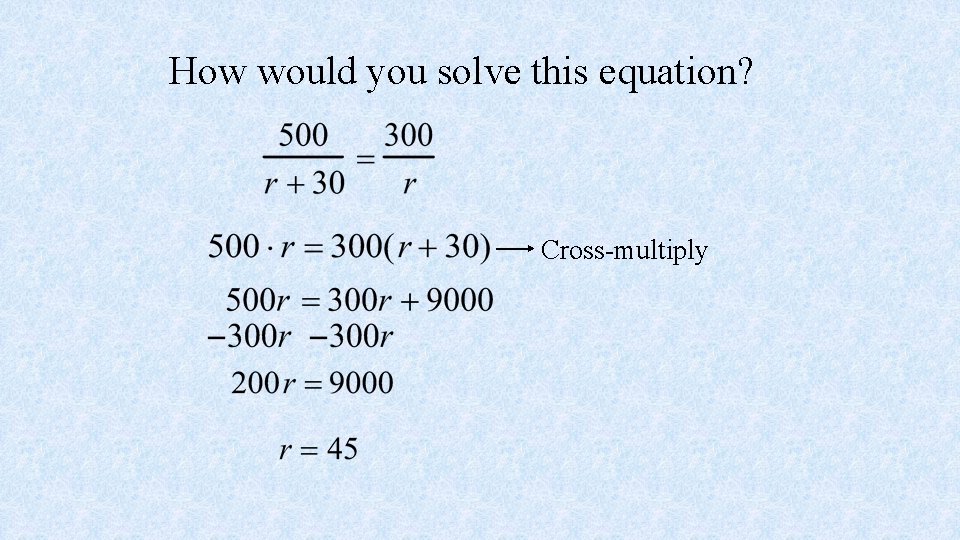

- Slides: 114

Unit 8: Radical & Rational Functions LG 8 -1 Radical Functions LG 8 -2 Rational Functions TEST 5/22 – the last day of school! remediation

LG 8 -1 Radical Functions 1) We will SOLVE them! Understand solving equations as a process of reasoning and explain the reasoning • MGSE 9 -12. A. REI. 2 Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise. 2) We will GRAPH them! Analyze functions using different representations • MGSE 9 -12. F. IF. 7 Graph square root, cube root functions expressed algebraically and show key features of the graph both by hand by using technology. • MGSE 9 -12. F. IF. 4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models the relationship between two quantities. Sketch a graph showing key features including: intercepts; interval where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; 3) We will ANALYZE them! Create equations that describe numbers or relationships • MGSE 9 -12. A. CED. 2 Create radical functions in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales. Interpret functions that arise in applications in terms of the context • MGSE 9 -12. F. IF. 5 Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes.

ENDURING UNDERSTANDINGS • Graph radical functions • Solve radical equations algebraically and graphically ESSENTIAL QUESTIONS • How can we extend arithmetic properties and processes to algebraic expressions and how can we use these properties and processes to solve problems? • Why are all solutions not necessarily the solution to an equation? How can you identify these extra solutions?

SELECTED TERMS AND SYMBOLS • Extraneous Solutions: A solution of the simplified form of the equation that does not satisfy the original equation. • Inequality: Any mathematical sentence that contains the symbols > (greater than), < (less than or equal to), or > (greater than or equal to).

EVIDENCE OF LEARNING By the conclusion of this unit, you should be able to demonstrate the following competencies: • Solve radical equations • Graph radical functions and identify key characteristics • Interpret solutions to graphs and equations given the context of the problem

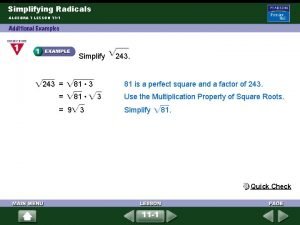
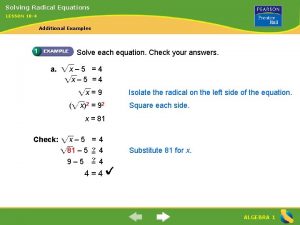
Solving radical equations • A radical equation contains a variable within a radical. • Recall that you can solve quadratic equations by taking the square root of both sides. Similarly, radical equations can be solved by raising both sides to a power.

Example 1: Solving Equations Containing One Radical

Example 2: Solving Equations Containing One Radical

Example 3: Solving Equations Containing Two Radicals

You Try! Example 4

Extraneous Solutions • Raising each side of an equation to an even power may introduce extraneous solutions. • You don’t have to worry about extraneous solutions when solving problems to an odd power.
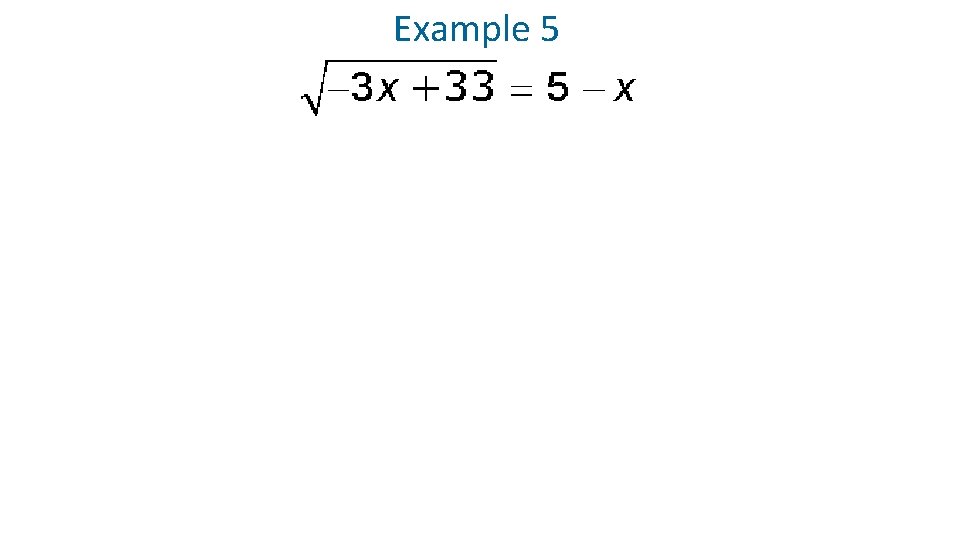
Example 5

You Try! Example 6
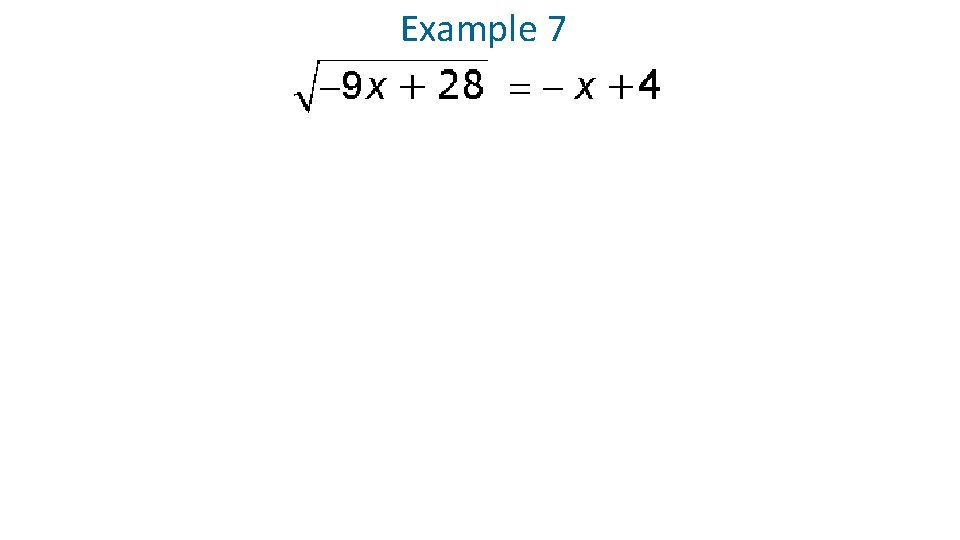
Example 7

Example 8: Solving Equations with Rational Exponents 1 3 (5 x + 7) = 3

Example 9: Solving Equations with Rational Exponents 1 2 x = (4 x + 8) 2
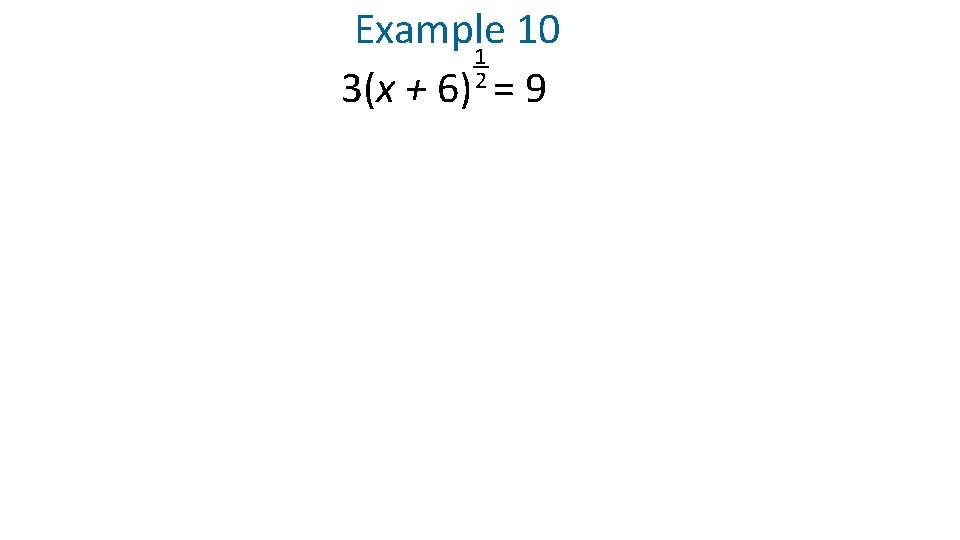
Example 10 1 2 3(x + 6) = 9

TOTD On a sticky note, please write your name and your answers to the following questions:

Class work/Homework: Page 462 #1 – 22

Warm Up 5/11

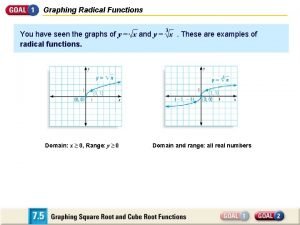
Graph of the Square Root x -1 0 1 4 y i 0 1 2 Square Root – “SHOOT Note: We cannot graph imaginary numbers on the coordinate plane. Therefore, the graph stops at x = 0.

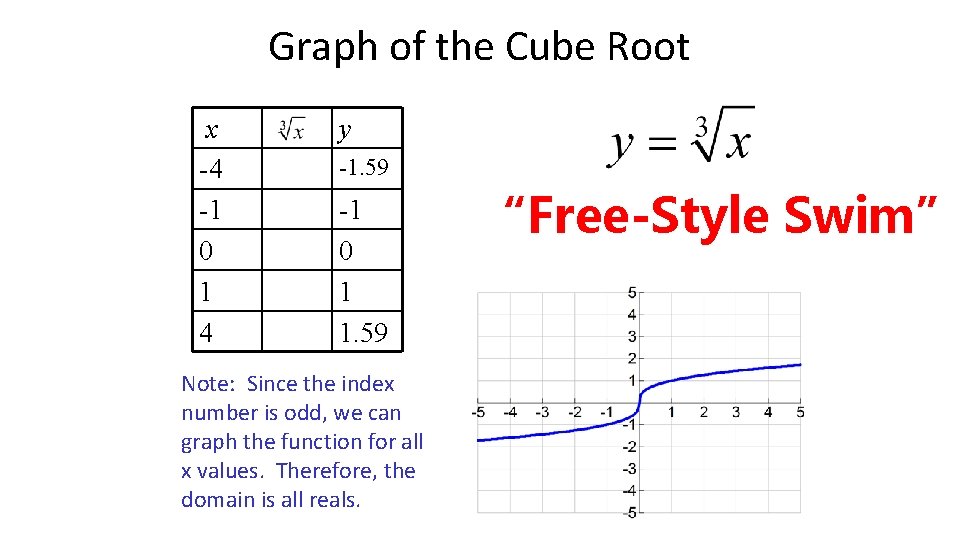
Graph of the Cube Root x -4 -1 0 1 4 y -1. 59 -1 0 1 1. 59 Note: Since the index number is odd, we can graph the function for all x values. Therefore, the domain is all reals. “Free-Style Swim”

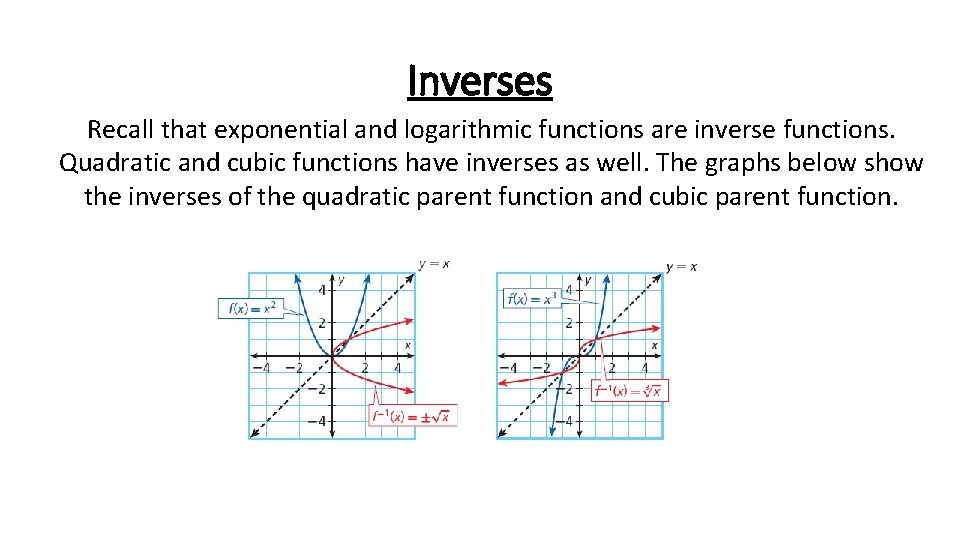
Inverses Recall that exponential and logarithmic functions are inverse functions. Quadratic and cubic functions have inverses as well. The graphs below show the inverses of the quadratic parent function and cubic parent function.
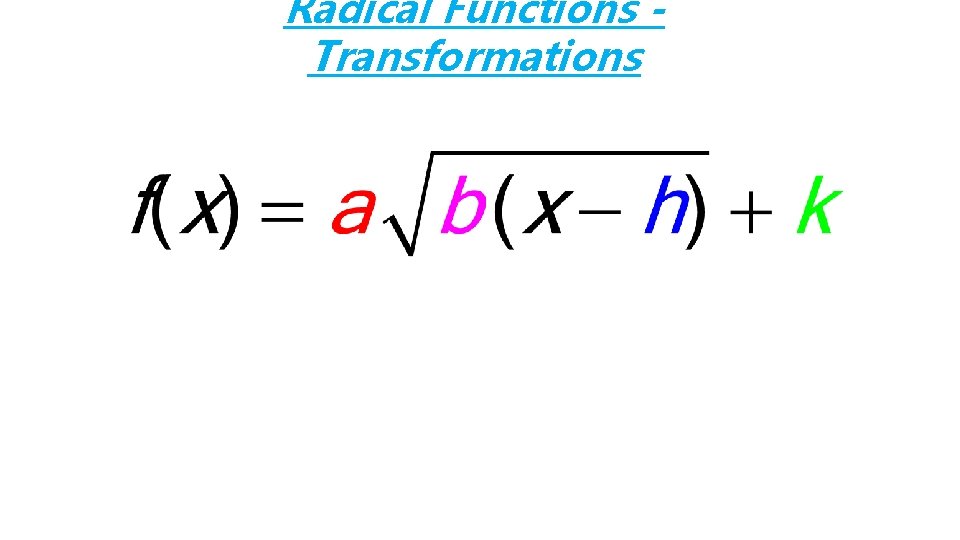
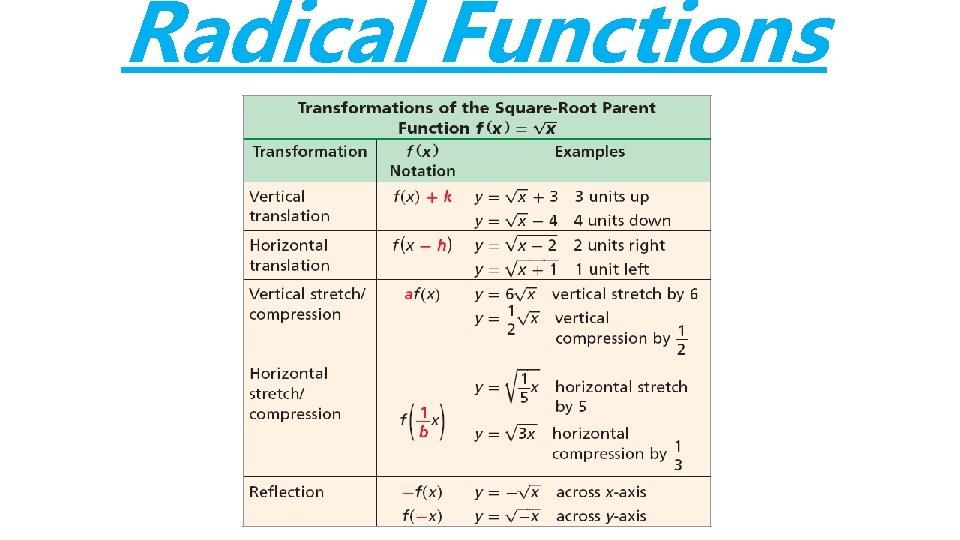
Radical Functions Transformations

Radical Functions Transformations When “a” is negative: Reflect over the x**Negative on the axis outside – it “x-caped”** When “a” is a fraction between 0 and 1: Vertical Shrink (Compression) When “a” is a number greater than 1:

Examples: Reflect over the x-axis Vertical Stretch by 2 Reflect over the x -axis, Vertical Shrink by 1/3

Radical Functions Transformations **Inside the radical, opposite of what you think** When “b” is negative: Reflect over the yaxis– “y” am I in here? ** **Negative on the inside When “b” is a fraction between 0 and 1: Horizontal Stretch When “b” is a number greater than 1:

Examples: Reflect over the y-axis Horizontal Shrink by 1/3 Horizontal Stretch by 4

Radical Functions Transformations **Inside the radical, opposite of what you think** If “h” is positive, then the graph moves left: Horizontal shift to the left If “h” is negative, then the graph moves right: Horizontal shift to the right

Radical Functions Transformations If “k” is positive, then the graph moves up: Vertical shift up If “k” is negative, then the graph moves down: Vertical shift down

Examples: Right 3 Down 5 Left 2, Up 4

Going Backwards: The parent function is reflected across the x-axis, stretched vertically by a factor of 4, and translated 1 unit up

Going Backwards: The parent function is stretched horizontally by a factor of 2, reflected across the y-axis, and translated 3 units left

Radical Functions - Graphing • Use your table to help find good points • “Starting point” will always be (h, k)

Radical Functions – Let’s Graph!!

Radical Functions

Describe how to obtain the graph of g from the graph of f. Vertical shift: 3 units up Horizontal shift: 5 units to the left Vertical shift: 4 units down Horizontal shift: 1 units to the right Vertical shift: 6 units up Horizontal shift: 1 units to the left

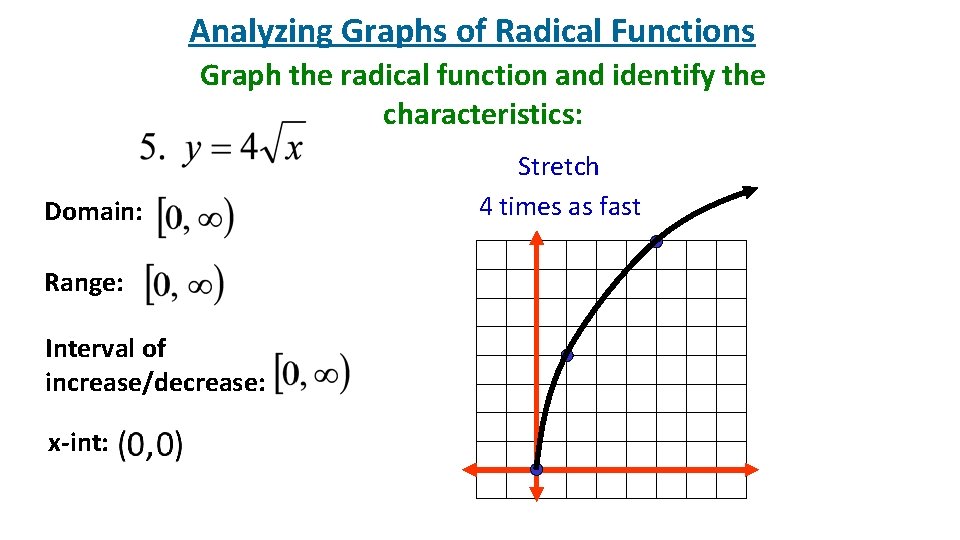
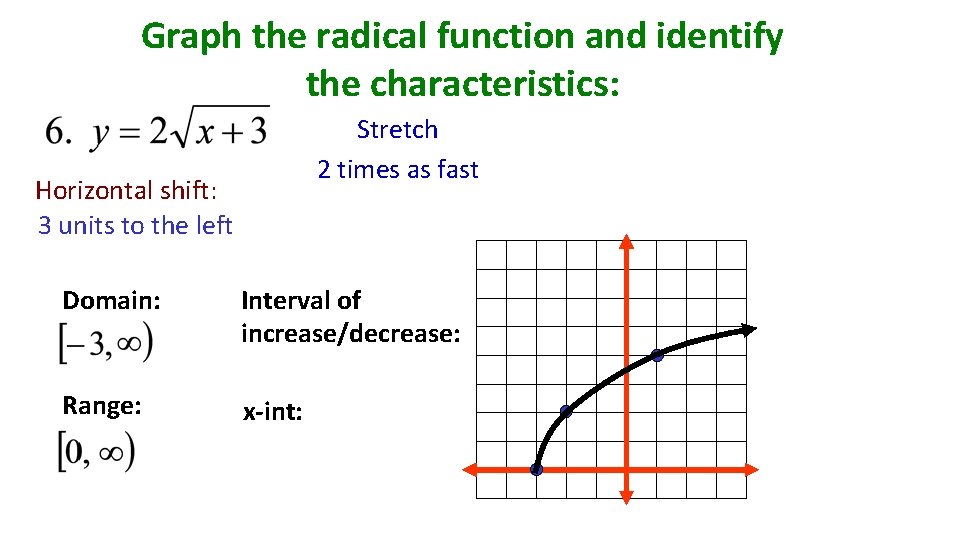
Analyzing Graphs of Radical Functions Graph the radical function and identify the characteristics: Domain: Range: Interval of increase/decrease: x-int: Stretch 4 times as fast

Graph the radical function and identify the characteristics: Stretch 2 times as fast Horizontal shift: 3 units to the left Domain: Interval of increase/decrease: Range: x-int:

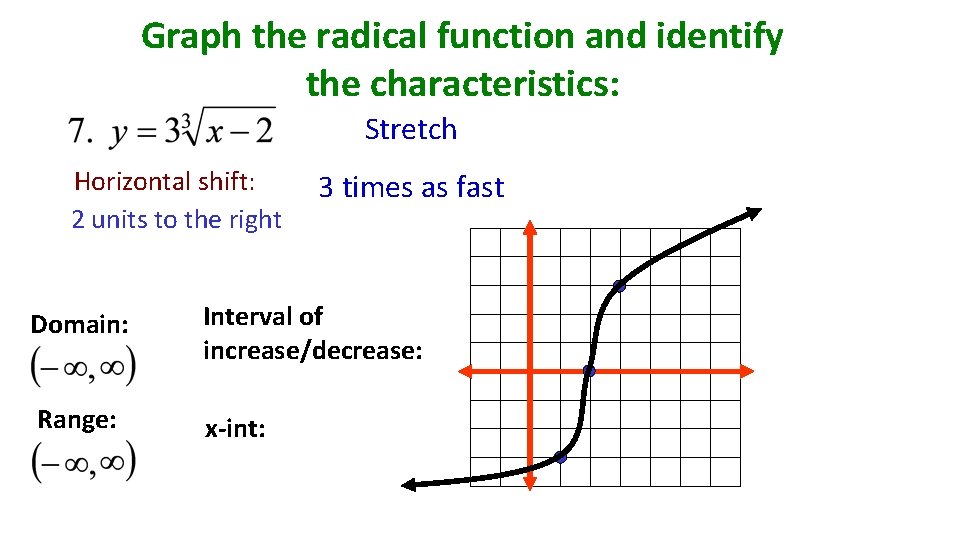
Graph the radical function and identify the characteristics: Stretch Horizontal shift: 2 units to the right 3 times as fast Domain: Interval of increase/decrease: Range: x-int:

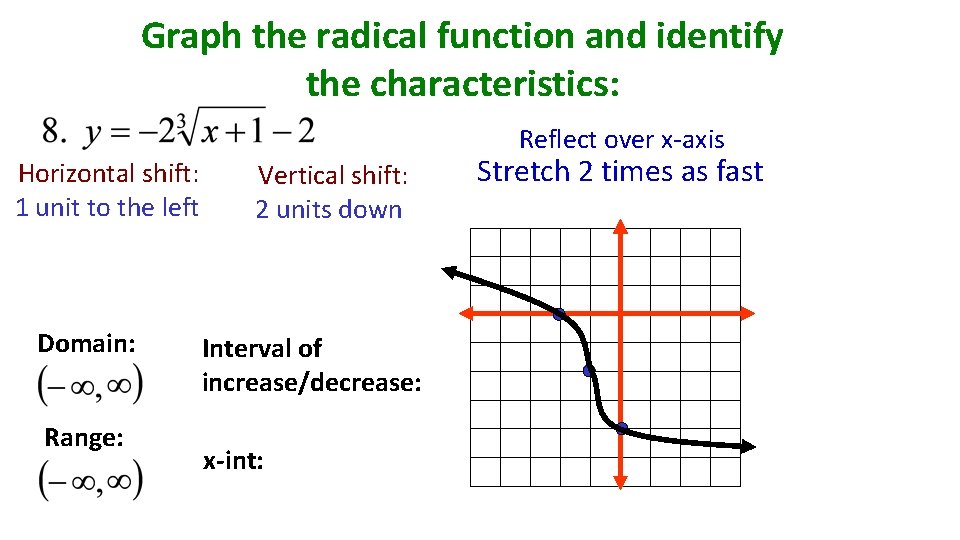
Graph the radical function and identify the characteristics: Reflect over x-axis Horizontal shift: 1 unit to the left Domain: Range: Vertical shift: 2 units down Interval of increase/decrease: x-int: Stretch 2 times as fast

Graph the radical function and identify the characteristics: Reflect over y-axis Stretch 2 times as fast Domain: Range: Interval of increase/decrease: x-int:

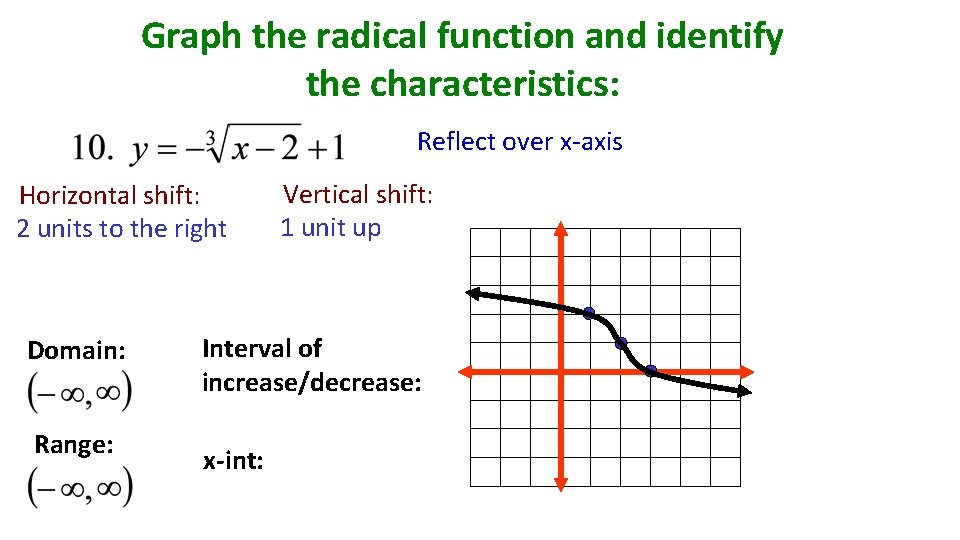
Graph the radical function and identify the characteristics: Reflect over x-axis Horizontal shift: 2 units to the right Domain: Range: Vertical shift: 1 unit up Interval of increase/decrease: x-int:

TOTD On a sticky note, please write your name and your answers to the following 3 questions:


Homework pg 454 # 24 - 38

Warm UP 5/12 Describe the transformations of the graph of each function. Then, state the domain, range, and intervals of increase or decrease.

Homework Check Silently answer the following questions on a sticky note and submit them. Don’t forget your name.

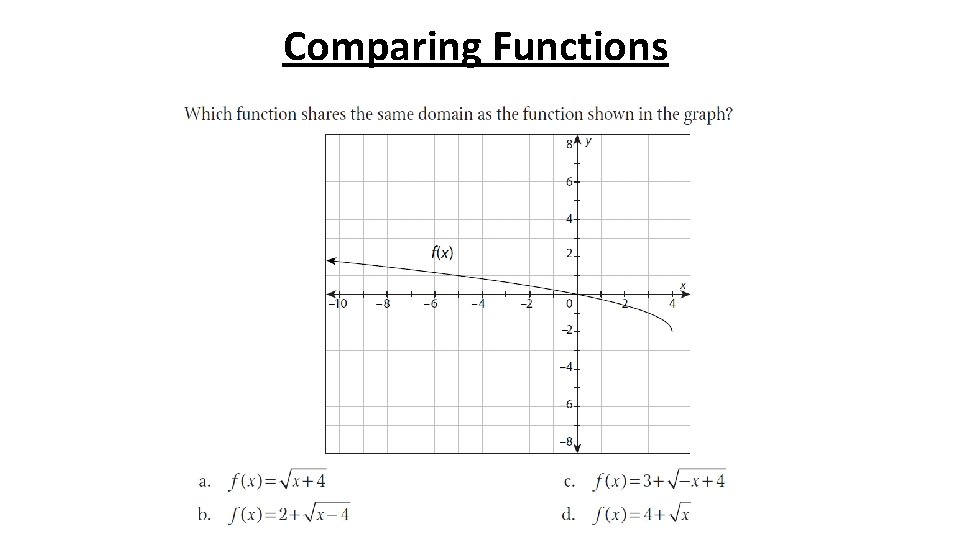
Comparing Functions

Comparing Functions

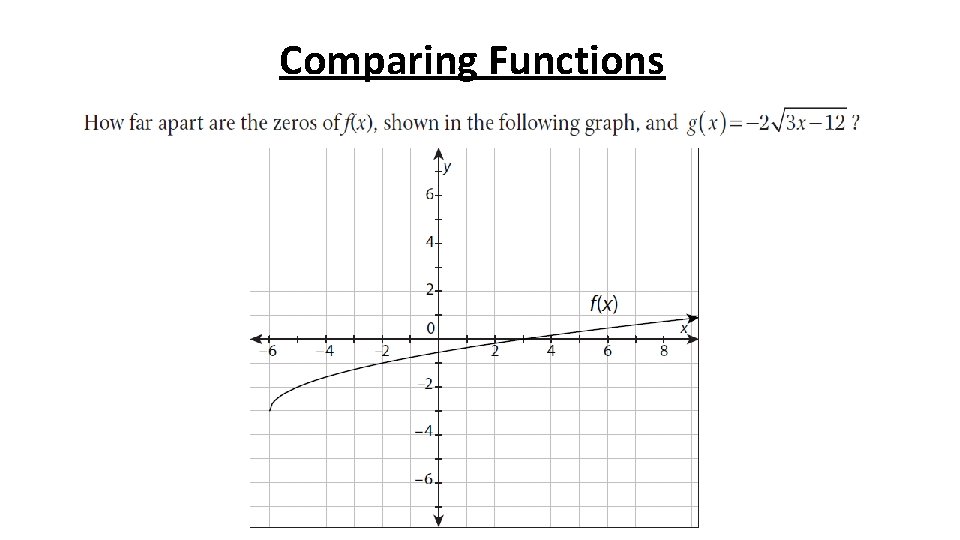
Comparing Functions

Comparing Functions

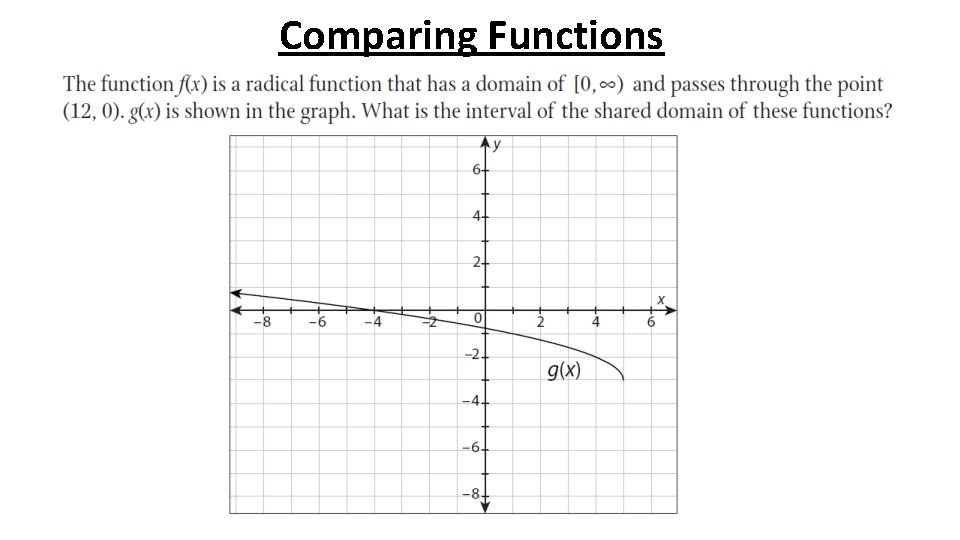
Comparing Functions

Comparing Functions

Comparing Functions

Comparing Functions

TOTD

Homework: Read pg 460 Example 5. Then, complete #23 – 25 on pg 462 and #42 – 44 on pg 463

Warm UP 5/15

Applications of Radical Functions The Pendulum Problem Gabriel visited the Museum of History and Technology with his physics class. They saw Focault’s Pendulum and it was fascinating to Gabe. He knew from physics class that the time it takes a pendulum to complete a full cycle or swing depends upon the length of the pendulum. The formula is given by where T represents the time in seconds and L represents the length of the pendulum in feet. He timed the swing of the pendulum with his watch and found that it took about 8 seconds for the pendulum to complete a full cycle. Help him figure out the length of the pendulum in feet.

The Pendulum Problem Jimmy thought that a pendulum that took a full 20 seconds to complete a full cycle would be very dramatic for a museum. How long must that pendulum be? If ceilings in the museum are about 20 feet high, would this pendulum be possible?

Classwork • Radical Characteristics Practice Worksheet

QUUEEEEEZZZZZ

Warm Up 5/16 F

LG 8 -2 Rational Functions Rewrite rational expressions • MGSE 9 -12. A. APR. 7 Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, multiplication, and division by a nonzero rational expression; add, subtract, multiply, and divide rational expressions. Create equations that describe numbers or relationships • MGSE 9 -12. A. CED. 1 Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear, quadratic, simple rational, and exponential functions (integer inputs only). • MGSE 9 -12. A. CED. 2 Create linear, quadratic, and exponential equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales. (The phrase “in two or more variables” refers to formulas like the compound interest formula, in which A = P(1 + r/n)nt has multiple variables. ) (Limit to radical and rational functions. ) Understand solving equations as a process of reasoning and explain the reasoning • MGSE 9 -12. A. REI. 2 Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise. Interpret functions that arise in applications in terms of the context • MGSE 9 -12. F. IF. 4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models the relationship between two quantities. Sketch a graph showing key features including: intercepts; interval where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity. (Limit to radical and rational functions. ) • MGSE 9 -12. F. IF. 5 Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function. (Limit to radical and rational functions. ) Analyze functions using different representations • MGSE 9 -12. F. IF. 7 Graph functions expressed algebraically and show key features of the graph both by hand by using technology. (Limit to radical and rational functions. ) • MGSE 9 -12. F. IF. 7 d Graph rational functions, identifying zeros and asymptotes when suitable factorizations are available, and showing end behavior.

ENDURING UNDERSTANDINGS • Recognize rational functions as the division of two polynomial functions and rewrite a rational expression • Find the sum, difference, product, and quotient of rational expressions • Graph rational functions • Interpret graphs and discover characteristics of rational functions • Solve rational equations algebraically and graphically • Solve rational inequalities

ESSENTIAL QUESTIONS • How can we extend arithmetic properties and processes to algebraic expressions and how can we use these properties and processes to solve problems? • How do the polynomial pieces of a rational function affect the characteristics of the function itself? • How are horizontal asymptotes, slant asymptotes, and vertical asymptotes alike and different? • Why are all solutions not necessarily the solution to an equation? How can you identify these extra solutions? • Why is it important to set a rational inequality to 0 before solving?

SELECTED TERMS AND SYMBOLS • Extraneous Solutions: A solution of the simplified form of the equation that does not satisfy the original equation. • Inequality: Any mathematical sentence that contains the symbols > (greater than), < (less than or equal to), or > (greater than or equal to). • Rational Function: The quotient of two polynomials • Reciprocal: Two numbers whose product is one.

EVIDENCE OF LEARNING By the conclusion of this unit, you should be able to demonstrate the following competencies: • Rewrite rational expressions in different forms • Add, subtract, multiply, and divide rational expressions • Solve rational equations • Solve rational inequalities • Graph rational functions and identify key characteristics • Interpret solutions to graphs and equations given the context of the problem
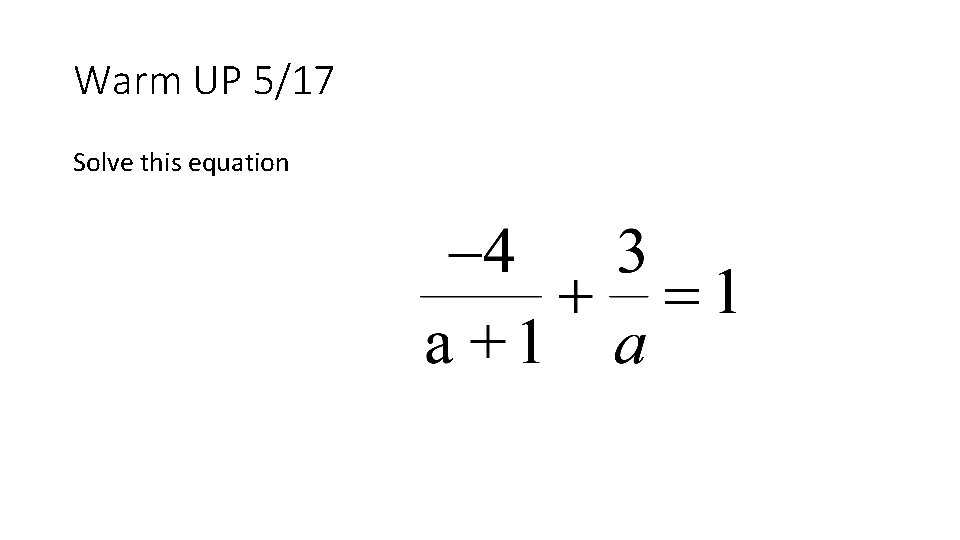
Warm UP 5/17 Solve this equation
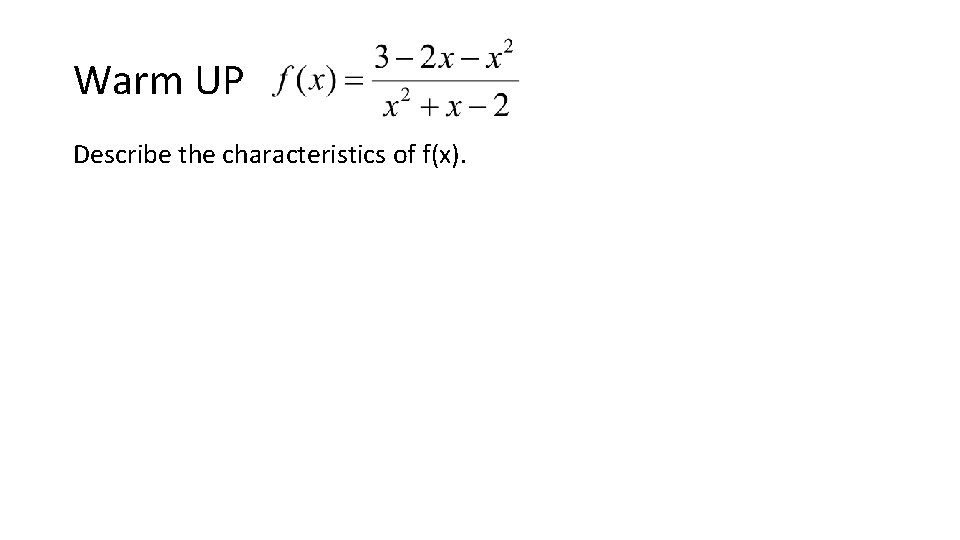
Warm UP Describe the characteristics of f(x).

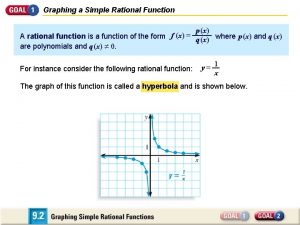
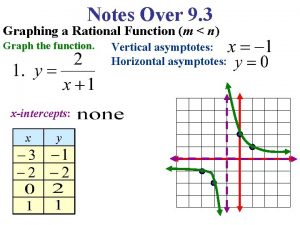
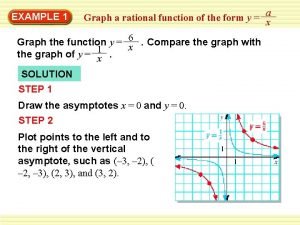
Graphing Rational Functions. . . (by hand) And more characteristics!

Behavior with asymptotes
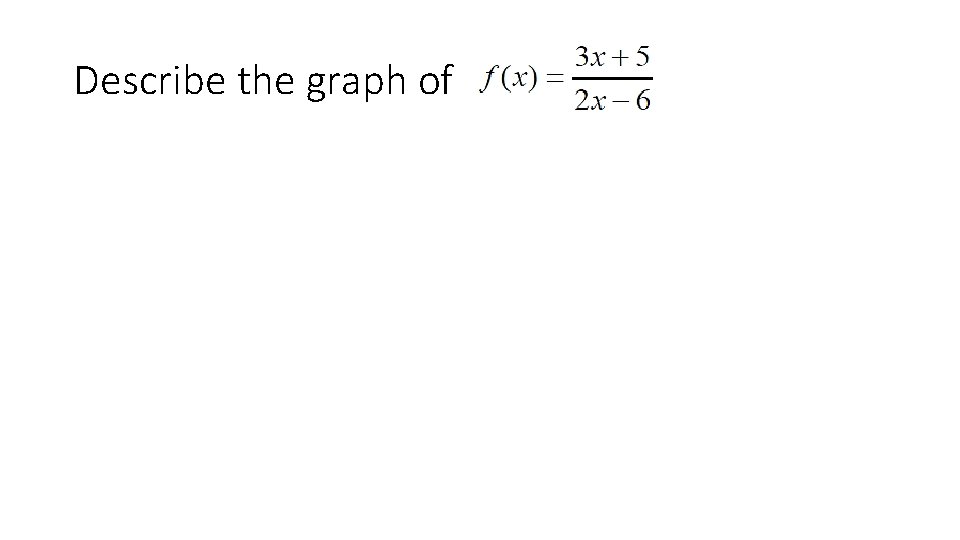
Describe the graph of
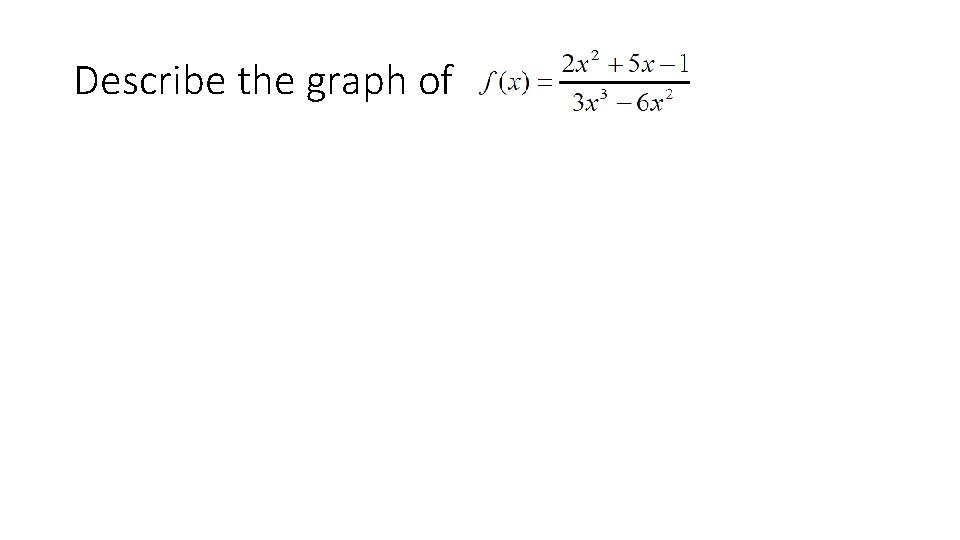
Describe the graph of
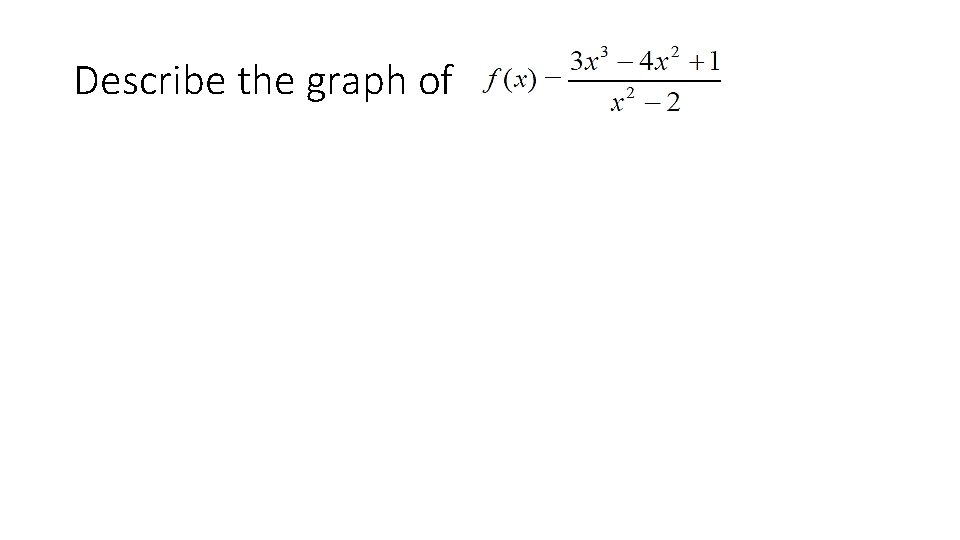
Describe the graph of

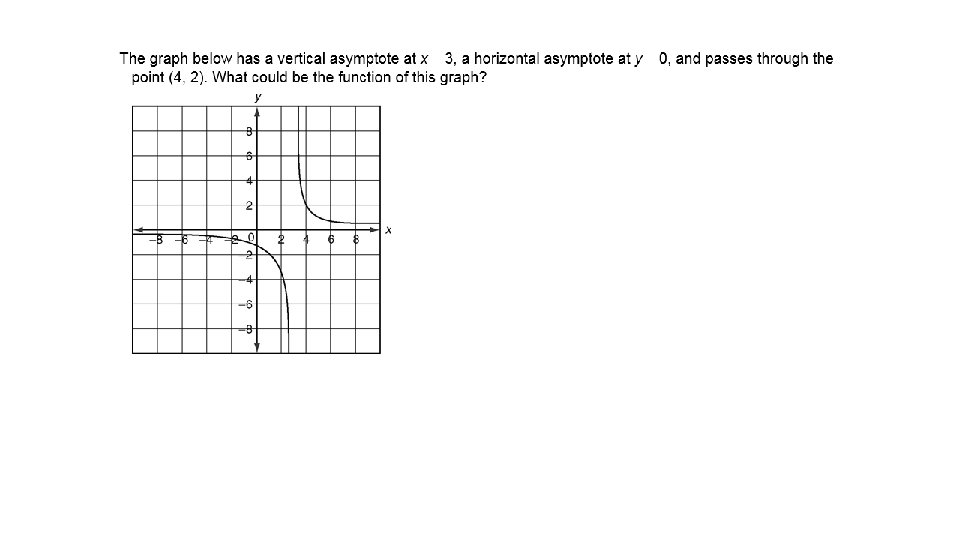
Warm UP! Describe the graph of

About those holes… Sometimes, a factor will appear in the numerator and in the denominator. Let's assume the factor (x-k) is in the numerator and denominator. Because the factor is in the denominator, x=k will not be in the domain of the function. This means that one of two things can happen. There will either be a vertical asymptote at x=k, or there will be a hole at x=k.

Let's look at what will happen in each of these cases. • There are more (x-k) factors in the denominator. After dividing out all duplicate factors, the (x-k) is still in the denominator. Factors in the denominator result in vertical asymptotes. Therefore, there will be a vertical asymptote at x=k.

Let's look at what will happen in each of these cases. • There are more (x-k) factors in the numerator. After dividing out all the duplicate factors, the (x-k) is still in the numerator. Factors in the numerator result in x-intercepts. But, because you can't use x=k, there will be a hole in the graph on the x-axis.

Let's look at what will happen in each of these cases. • There are equal numbers of (x-k) factors in the numerator and denominator. After dividing out all the factors (because there are equal amounts), there is no (x-k) left at all. Because there is no (x-k) in the denominator, there is no vertical asymptote at x=k. Because there is no (x-k) in the numerator, there is no x-intercept at x=k. There is just a hole in the graph, someplace other than on the x-axis. To find the exact location, plug in x=k into the reduced function (you can't plug it into the original, it's undefined, there), and see what y-value you get.
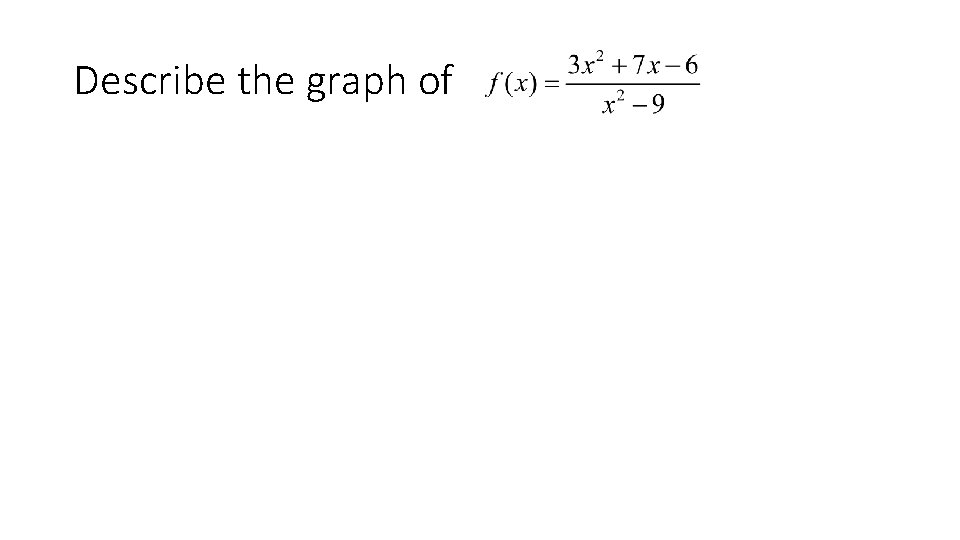
Describe the graph of
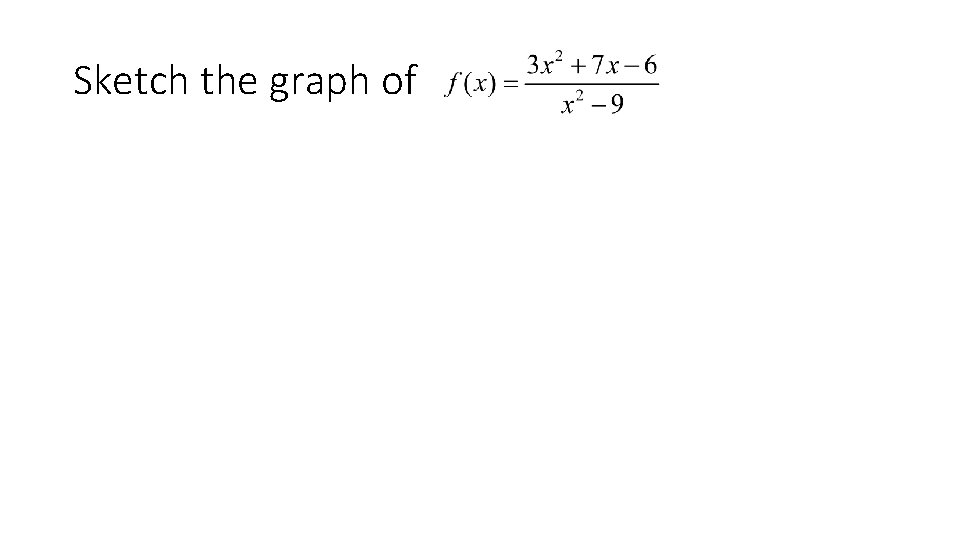
Sketch the graph of

Steps to describing and graphing (by hand): 1) 2) 3) 4) 5) 6) 7) Factor numerator and denominator Locate any holes (if applicable) and plot Sketch the vertical asymptote(s) Sketch the HA or SA and find intersections with asymptotes Plot x and y intercepts Make a sign chart Connect the “dots”!

Practice – 8 graphs DO THEM ALL EVEN IF YOU DON’T WANT TO DO THEM BECAUSE I SAID SO
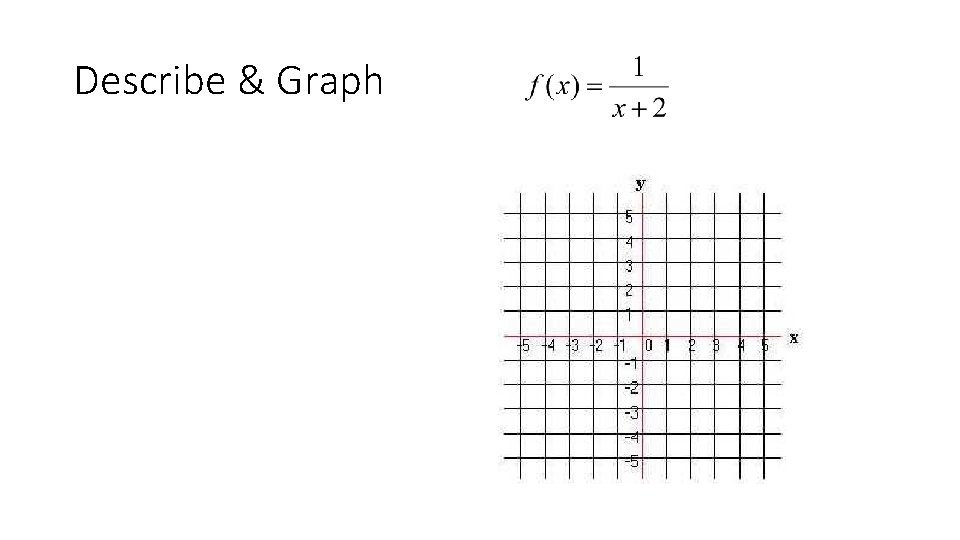
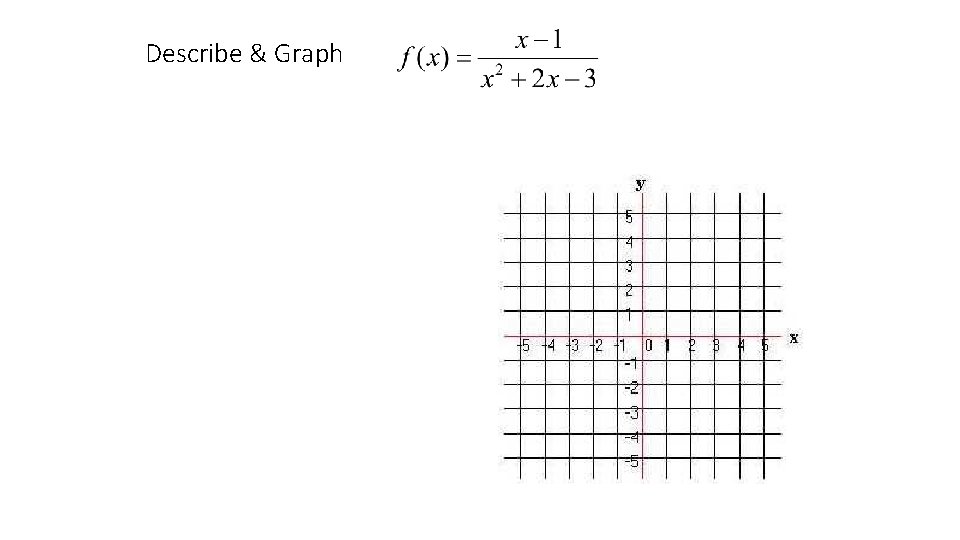
Describe & Graph
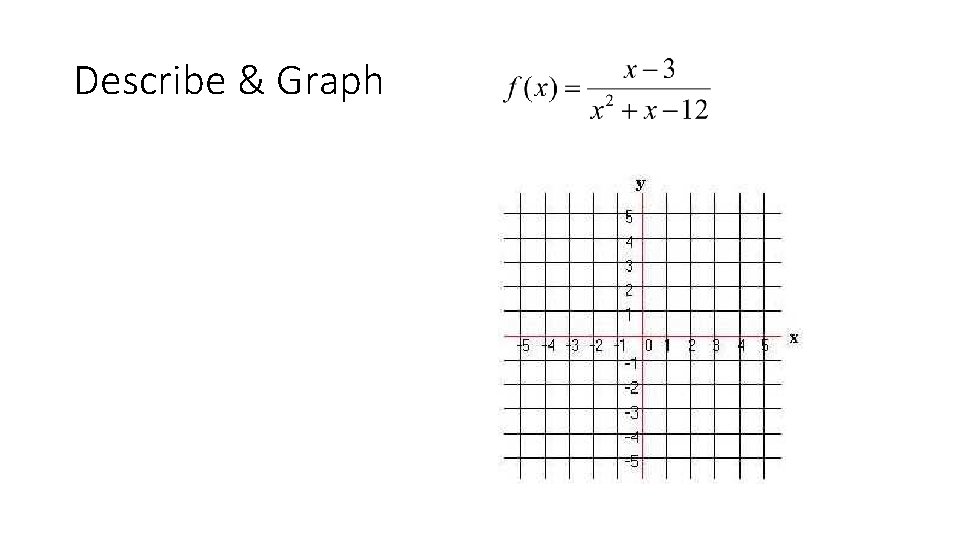
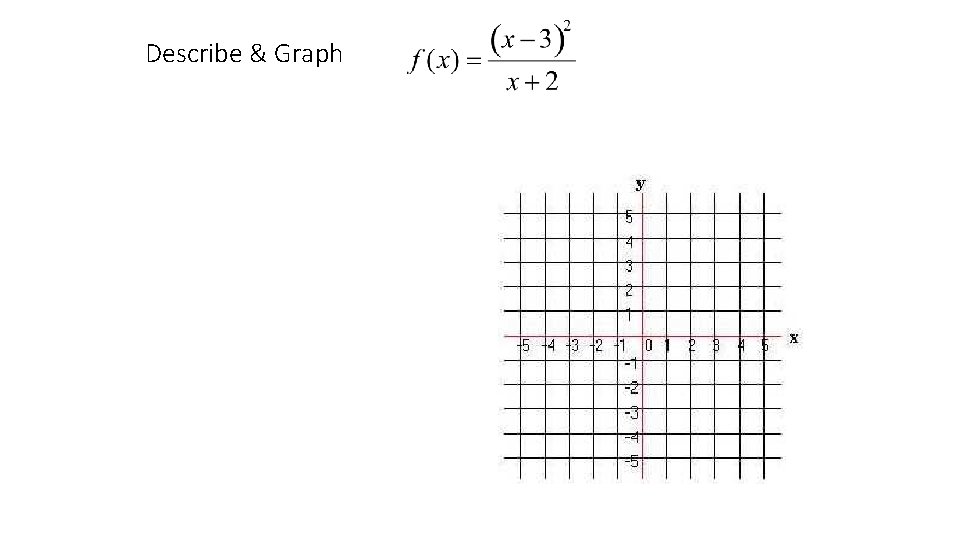
Describe & Graph
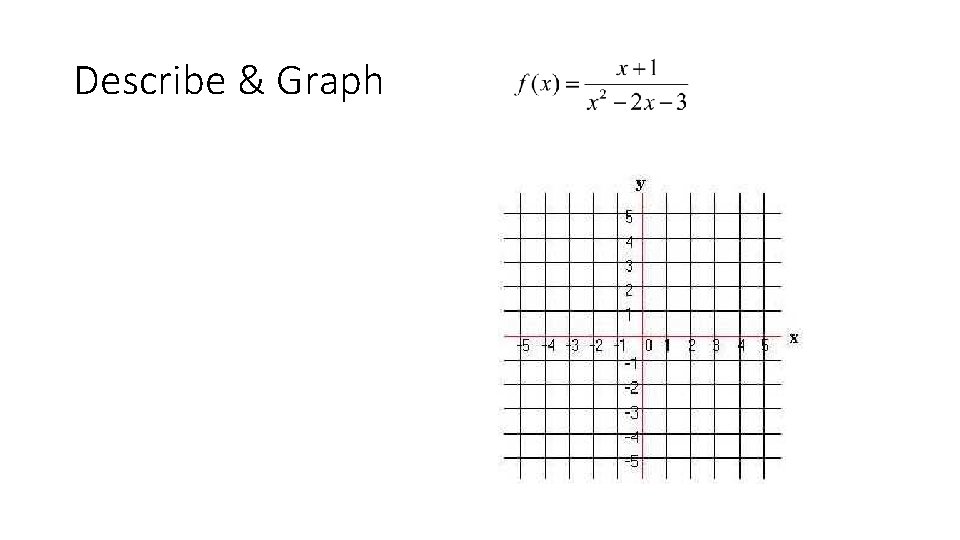
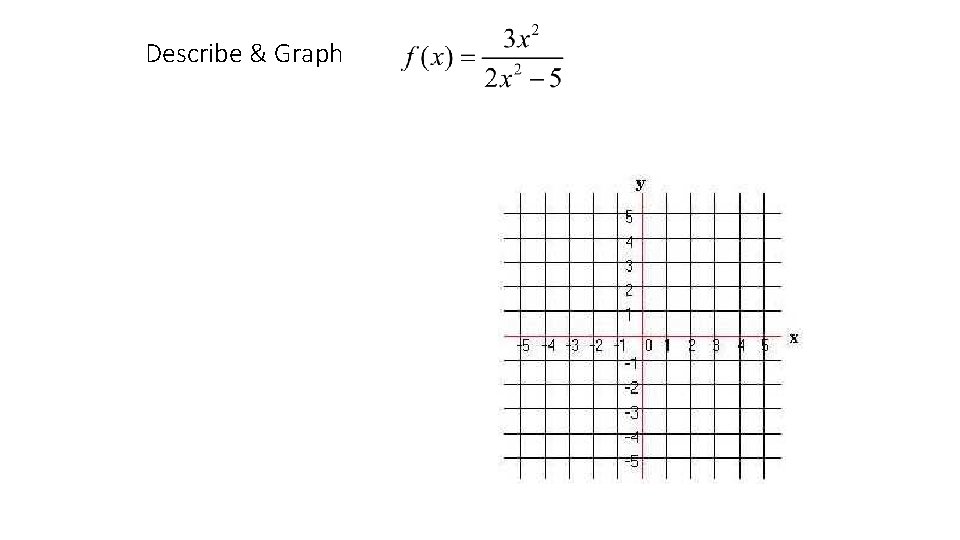
Describe & Graph
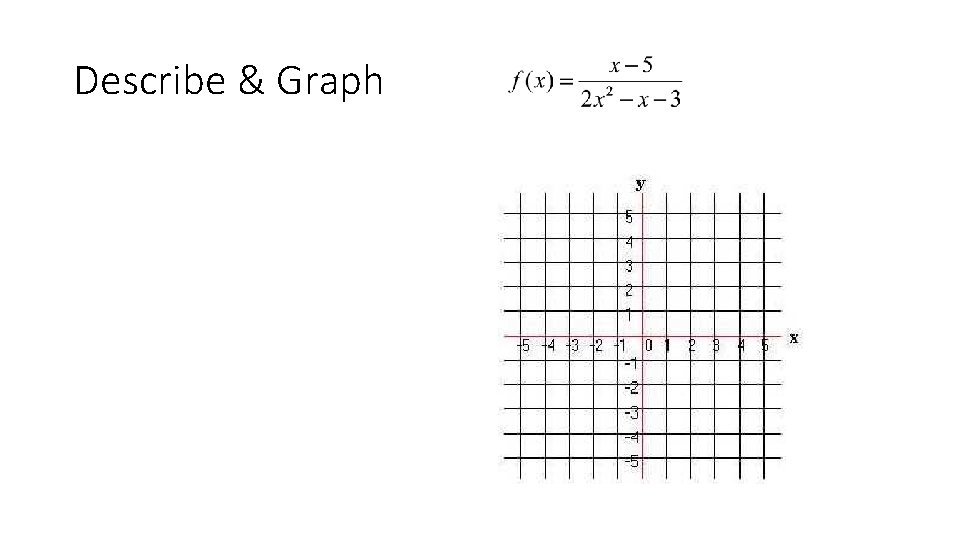
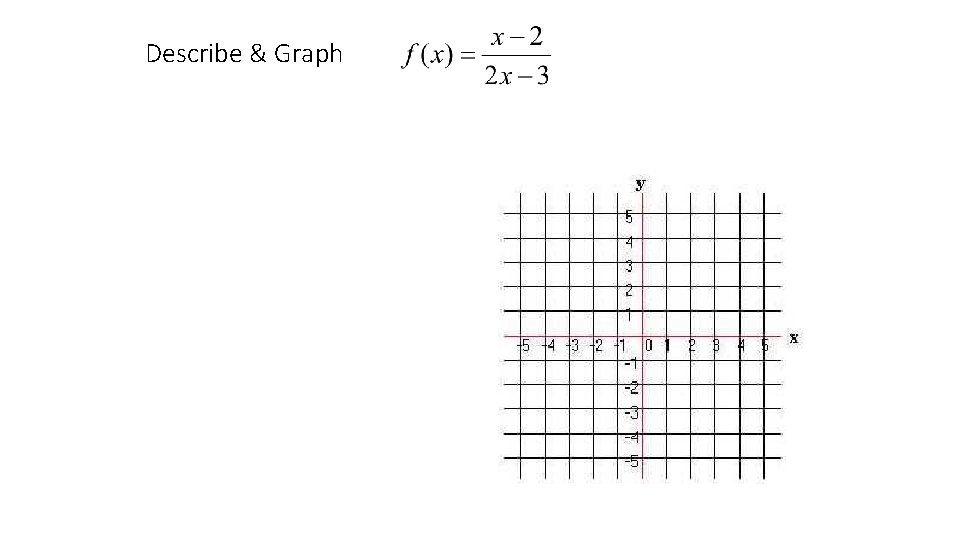
Describe & Graph

Describe & Graph

Describe & Graph

Describe & Graph

Describe & Graph

Warm UP! Sketch the graph WITHOUT USING A CALCULATOR! Then determine the characteristics: Domain: Range: End Behavior: Intervals of Increase/Decrease:


Solving Equations Containing

First, we will look at solving these problems algebraically. Here is an example that we will do together using two different methods.

The best way to solve a rational equation: This can be done by multiplying each side of the equation by the LCD.
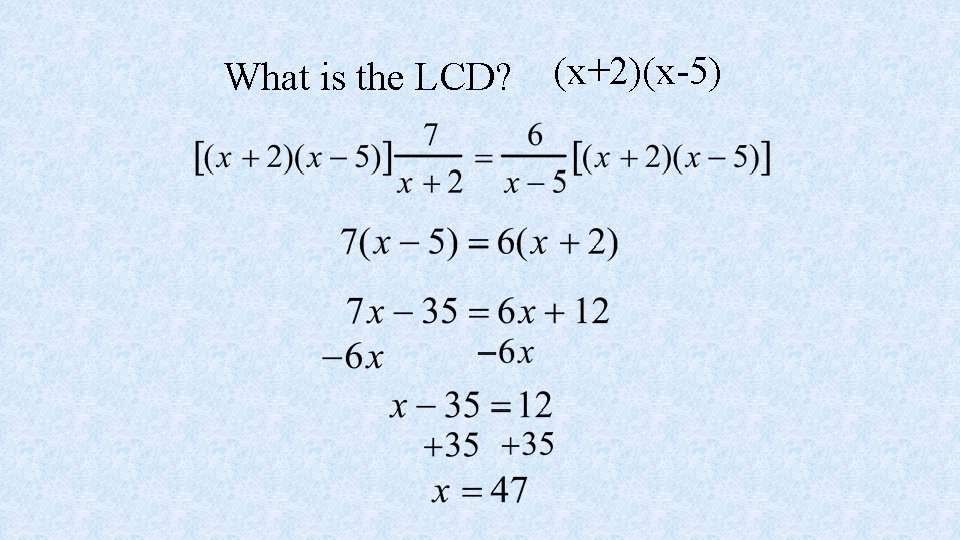
What is the LCD? (x+2)(x-5)

It is VERY important that you check your answers!!!!!!!!! Check:

The other method of solving rational equations is cross-multiplication.
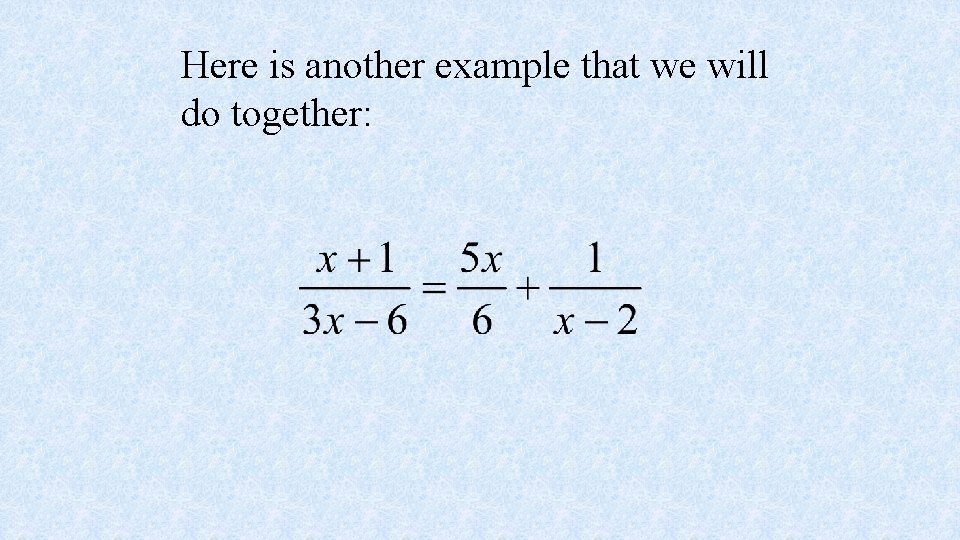
Here is another example that we will do together:

Step 1: Find the LCD Hint: Factor the denominator This denominator can be factored into 3(x-2) Therefore….
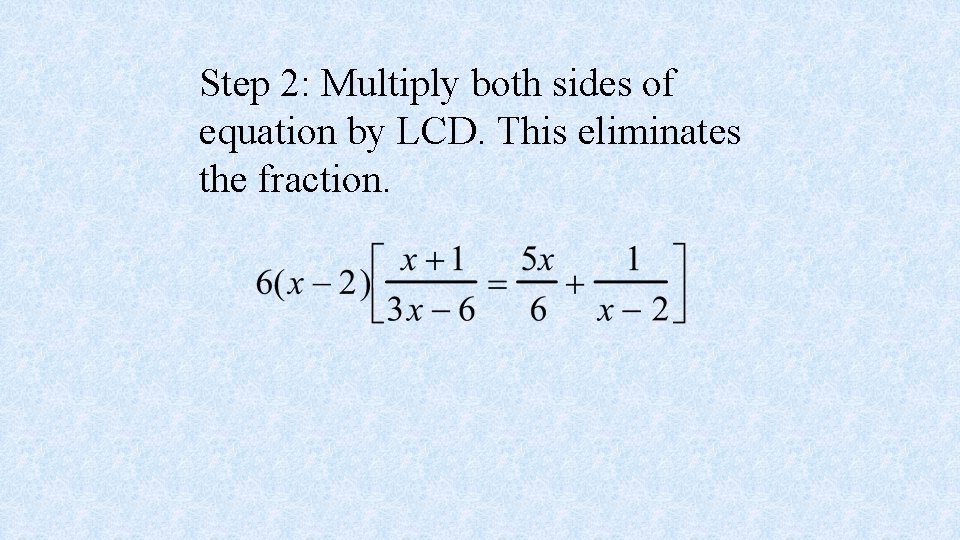
Step 2: Multiply both sides of equation by LCD. This eliminates the fraction.
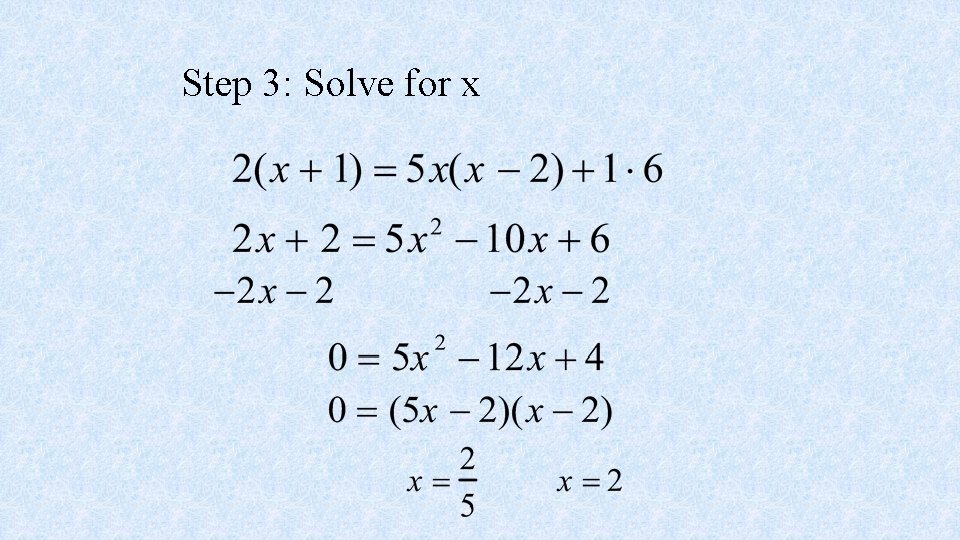
Step 3: Solve for x

Since there are two answers, there needs to be two checks. Let x =

Check #2: Let x = 2 When you check the number 2, you get a zero in the denominator. This means that 2 can not be a solution.
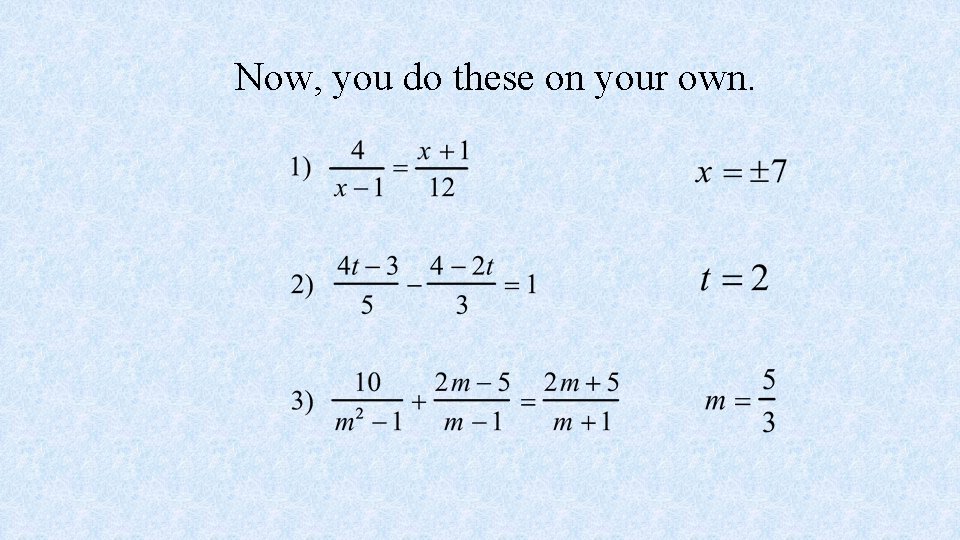
Now, you do these on your own.

Example #3: A car travels 500 miles in the same time that a train travels 300 miles. The speed of the car is 30 miles per hour faster than the speed of the train. Find the speed of the car and the train.

Remember the formula d=rt where: r = rate of speed d = distance t = time Since both vehicles travel the same amount of time, solve the formula for t.

Identify the variables that you are going to use. Let r = speed of the train How do you represent the speed of the car? Let r+30 = speed of the car
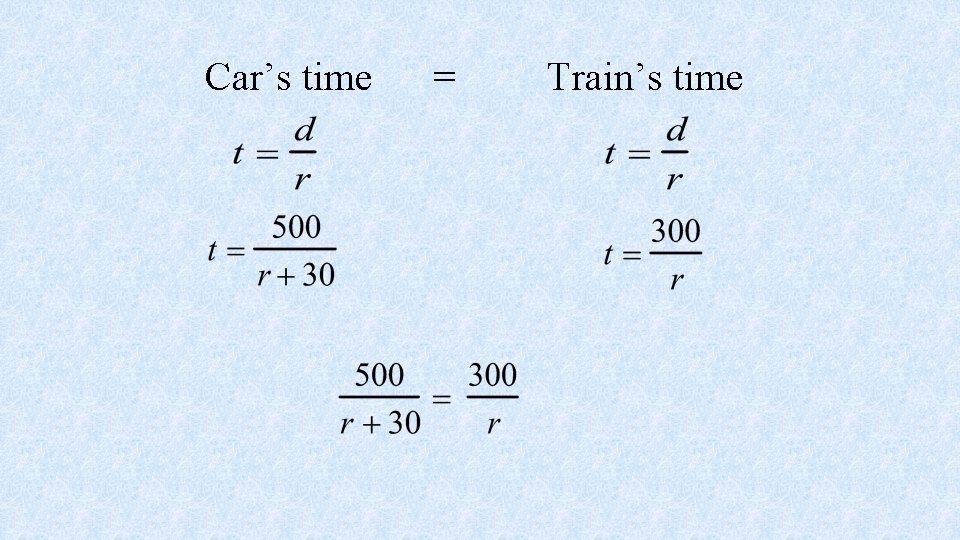
Car’s time = Train’s time
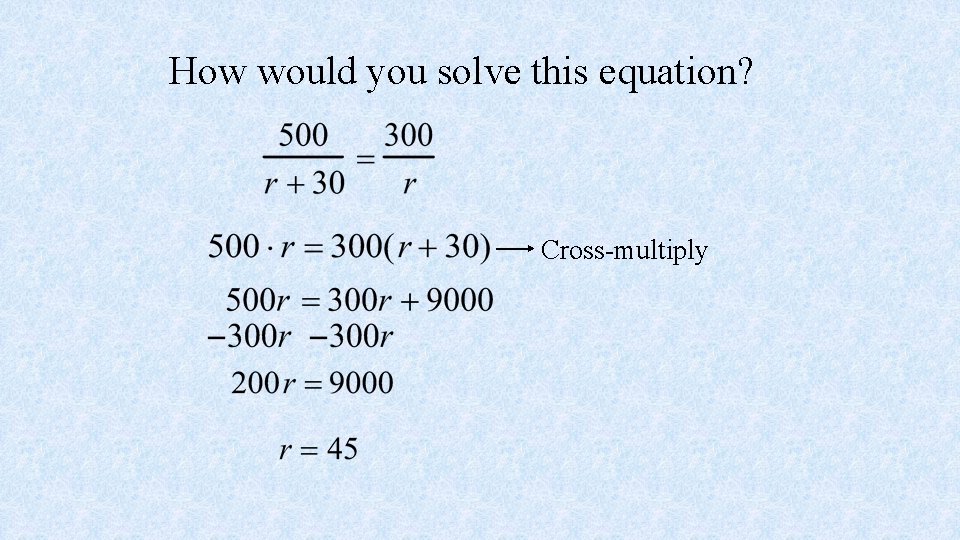
How would you solve this equation? Cross-multiply

Make sure that you answer the question. ANSWER: The car travels at a speed of 75 mph The train travels at a speed of 45 mph
 Radical functions and rational exponents unit test
Radical functions and rational exponents unit test Quiz 6-1 radicals and rational exponents answers
Quiz 6-1 radicals and rational exponents answers Unit 6 radical functions homework 8
Unit 6 radical functions homework 8 Radical functions and rational exponents practice
Radical functions and rational exponents practice Radical and rational functions
Radical and rational functions Rational exponents
Rational exponents F(3)
F(3) What is a mixed radical
What is a mixed radical Mixed radical to entire radical
Mixed radical to entire radical Unit 8 rational functions homework 1
Unit 8 rational functions homework 1 Asymptote rules
Asymptote rules Equations with rational exponents
Equations with rational exponents 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents Rational exponent to radical form calculator
Rational exponent to radical form calculator 5-6 radical expressions and rational exponents
5-6 radical expressions and rational exponents Radical and rational expressions
Radical and rational expressions Practice 11-1 simplifying radicals answers
Practice 11-1 simplifying radicals answers Solving rational equations and inequalities
Solving rational equations and inequalities Apa itu tuxedo
Apa itu tuxedo 7 radical din 5
7 radical din 5 Biologists have discovered that the shoulder height h
Biologists have discovered that the shoulder height h Unit 6 review questions
Unit 6 review questions Vertical
Vertical Rational function parent function
Rational function parent function Parent rational function
Parent rational function Rational expressions and functions
Rational expressions and functions What are rational functions
What are rational functions Limits of rational functions
Limits of rational functions Degree of denominator
Degree of denominator Range of rational function
Range of rational function Rational function is a function of the form
Rational function is a function of the form Rational and irrational functions
Rational and irrational functions Rational functions holes and asymptotes
Rational functions holes and asymptotes Rational function project
Rational function project Gina wilson rational functions
Gina wilson rational functions How to find end behavior of a function
How to find end behavior of a function 8-3 practice rational functions and their graphs
8-3 practice rational functions and their graphs Chapter 4 polynomial and rational functions
Chapter 4 polynomial and rational functions Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Horizontal asymptote rules
Horizontal asymptote rules State the excluded values for each rational expression
State the excluded values for each rational expression Analyzing rational functions
Analyzing rational functions Rational functions in medicine
Rational functions in medicine Algebra 2b unit 3
Algebra 2b unit 3 Rational functions and their graphs
Rational functions and their graphs Long run behavior of rational functions
Long run behavior of rational functions Graphing rational functions quiz
Graphing rational functions quiz Graphing rational functions
Graphing rational functions Rational function characteristics
Rational function characteristics Synthetic divison
Synthetic divison Is it rational
Is it rational Polynomial functions grade 12
Polynomial functions grade 12 Inverse of a rational function
Inverse of a rational function Graphing rational functions
Graphing rational functions 2-5 rational functions
2-5 rational functions Ib math sl rational functions questions
Ib math sl rational functions questions What is a rational function
What is a rational function Simplifying rational functions
Simplifying rational functions How to find vertical asymptotes of a function
How to find vertical asymptotes of a function Rational graph
Rational graph Lesson 3: rational functions and their graphs
Lesson 3: rational functions and their graphs Graph rational functions
Graph rational functions Ratey algebra 2
Ratey algebra 2 Rational function summary
Rational function summary Rational function
Rational function Is 43 rational or irrational
Is 43 rational or irrational Rational functions grapher
Rational functions grapher Non rational numbers
Non rational numbers Rational functions grapher
Rational functions grapher Chapter 3 polynomial and rational functions
Chapter 3 polynomial and rational functions Glue a picture for each greeting below
Glue a picture for each greeting below How to find slant asymptotes
How to find slant asymptotes Piecewise function absolute value
Piecewise function absolute value Evaluating functions
Evaluating functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Unit 8 review logarithms
Unit 8 review logarithms Algebra 2 unit 5 polynomial functions quiz 5-1 answers
Algebra 2 unit 5 polynomial functions quiz 5-1 answers Unit 5 polynomial functions
Unit 5 polynomial functions Examples of exponential equations
Examples of exponential equations Closure property of polynomials
Closure property of polynomials Formalizing relations and functions answers
Formalizing relations and functions answers Pg
Pg Formalizing relations and functions
Formalizing relations and functions Unit 2 linear functions homework 2
Unit 2 linear functions homework 2 Trigonometric functions and the unit circle
Trigonometric functions and the unit circle Trigonometric functions unit circle approach
Trigonometric functions unit circle approach Diagram of system unit
Diagram of system unit Trigonometric functions unit circle approach
Trigonometric functions unit circle approach Verbos con cambio radical
Verbos con cambio radical Verbos de cambio radical
Verbos de cambio radical Radical psychiatry sociology
Radical psychiatry sociology Innovacion semi radical
Innovacion semi radical Radical republicans def
Radical republicans def Radical pluralist account of penal crisis
Radical pluralist account of penal crisis Behaviorismo skinner
Behaviorismo skinner Property of radicals
Property of radicals Radical resource productivity
Radical resource productivity Initiation radical reaction
Initiation radical reaction Solving square root and other radical equations
Solving square root and other radical equations 10-4 skills practice radical equations answers with work
10-4 skills practice radical equations answers with work Inequalities with radicals
Inequalities with radicals Solving radical equations and inequalities
Solving radical equations and inequalities Are radicals irrational
Are radicals irrational Simplifying radicals worksheet doc
Simplifying radicals worksheet doc Index in radicals
Index in radicals How to simplify radical expressions algebra 1
How to simplify radical expressions algebra 1 Simplify radical 108
Simplify radical 108 Radical form
Radical form Unit 11 radicals homework 5 dividing radicals day 1
Unit 11 radicals homework 5 dividing radicals day 1 Evaluating rational exponents
Evaluating rational exponents La revisión fundamental y el rediseño radical de procesos
La revisión fundamental y el rediseño radical de procesos Realidad radical
Realidad radical How to get a radical out of the denominator
How to get a radical out of the denominator Process of removing the radical sign in the denominator
Process of removing the radical sign in the denominator Square root of 61 in radical form
Square root of 61 in radical form