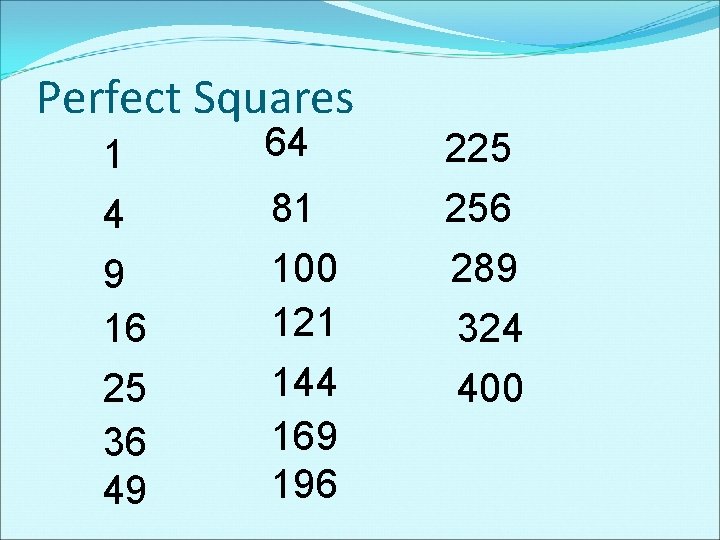
Simplifying Radicals Perfect Squares 1 4 9 16


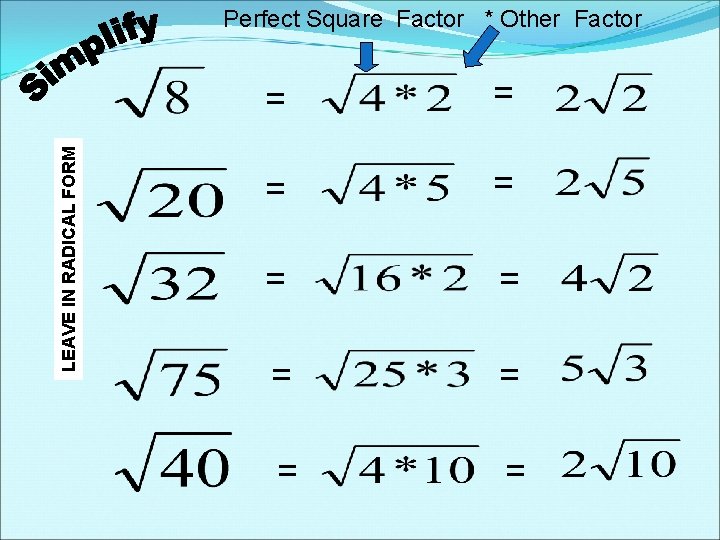




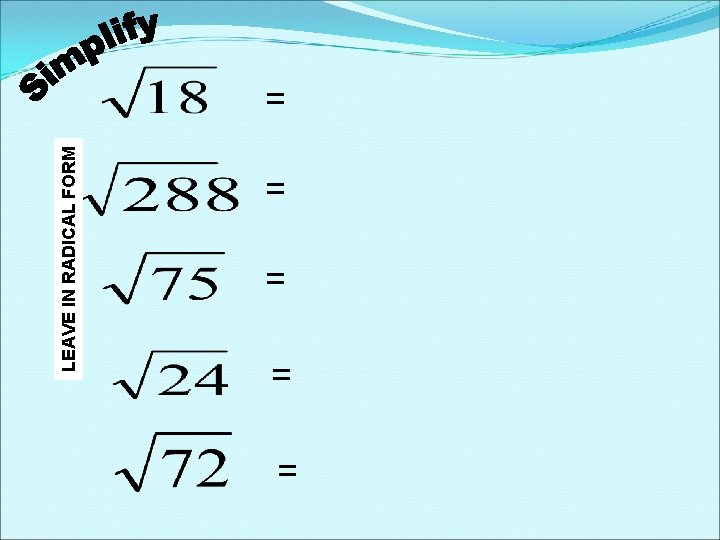
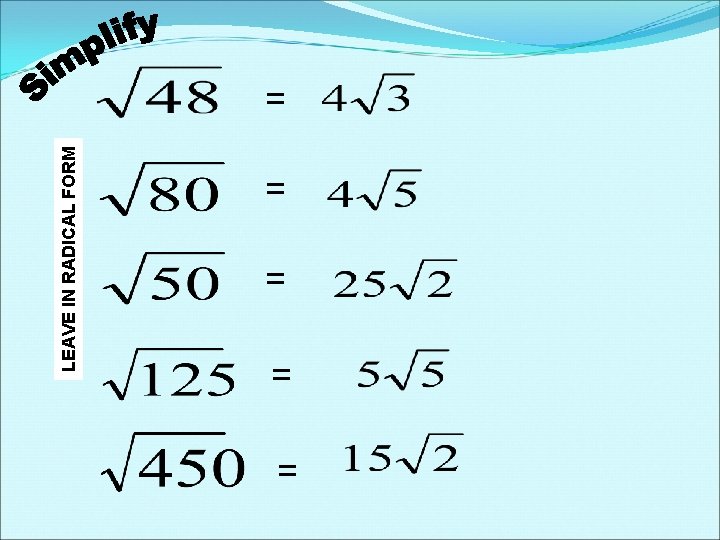



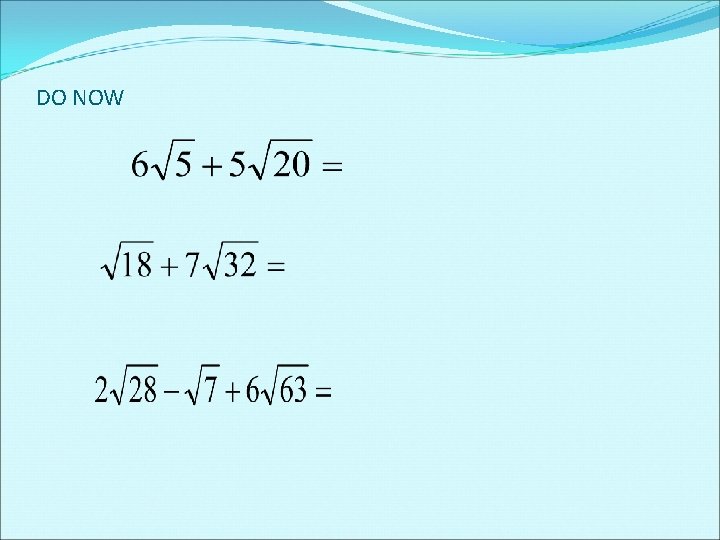


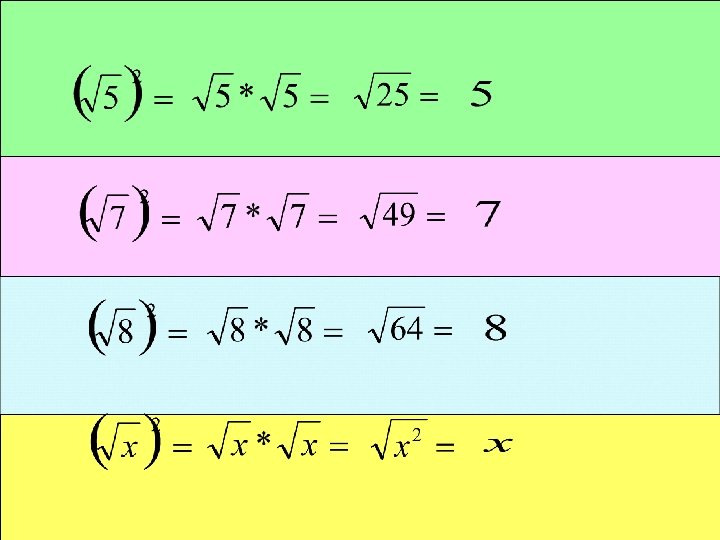








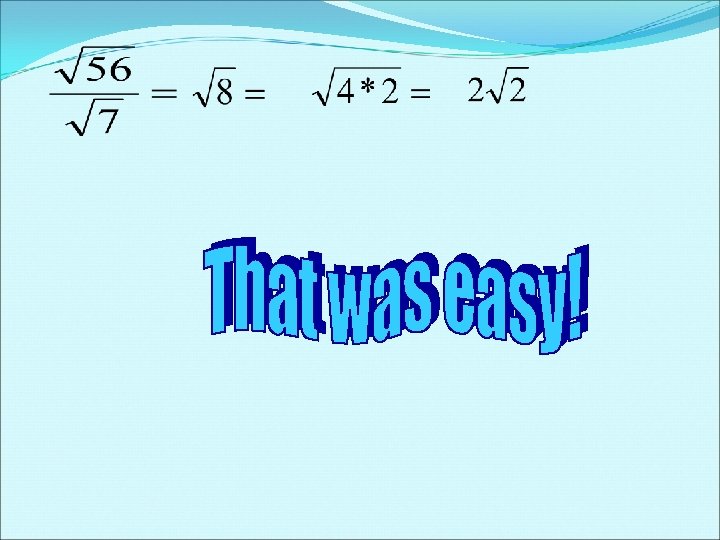




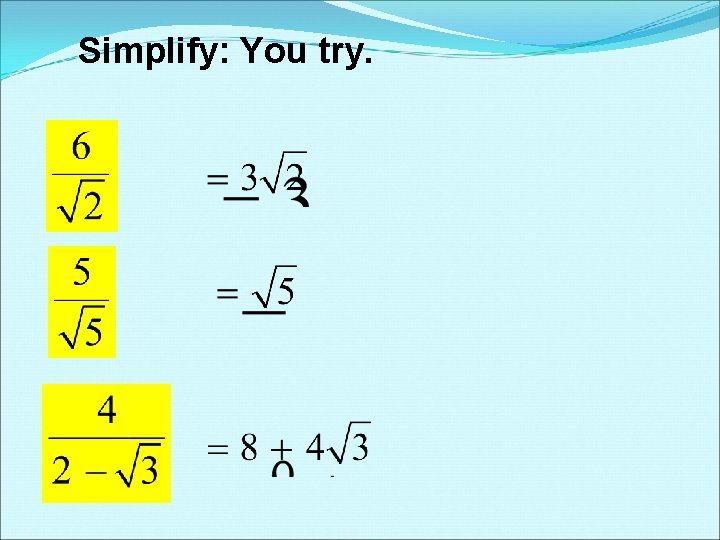




- Slides: 35

Simplifying Radicals

Perfect Squares 1 4 9 16 25 36 49 64 225 81 100 121 144 169 196 256 289 324 400

=2 =4 =5 = 10 = 12
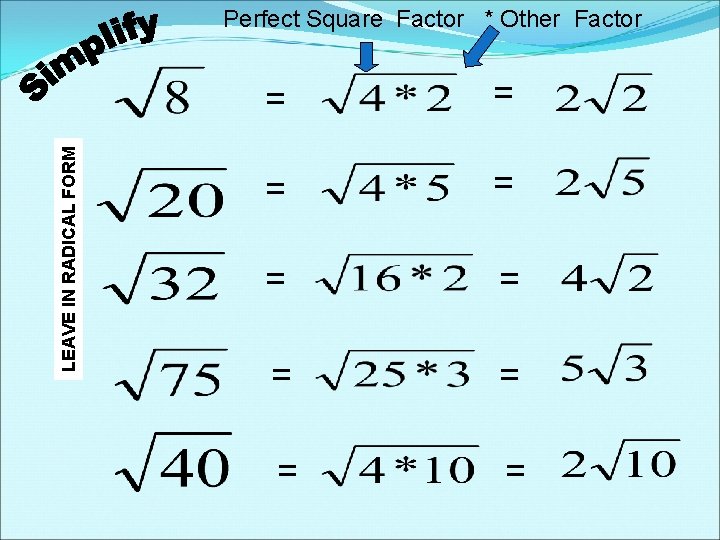
LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor = = = = =

Simplifying Radicals by Tree Method. Simplify the following. Step one, break the number down into a factor tree. Step two: Circle any pairs. 10 2 2 5

So… which is really just… The pair(s)go outside of the radical sign, but you only use one of them to represent the pair. Any term that is not a pair stays under the radical sign. Thus, the solution is …

Another Example Simplify the following: Step 1: Make a factor tree 10 14 2 So that leaves: Which is: 7 2 5

Your Turn! Simplify the following: 1. 2. 3. 4. 8
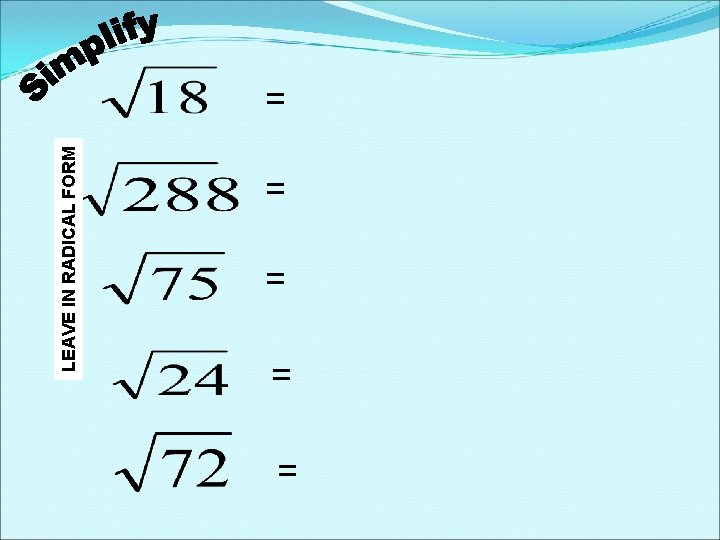
LEAVE IN RADICAL FORM = = =
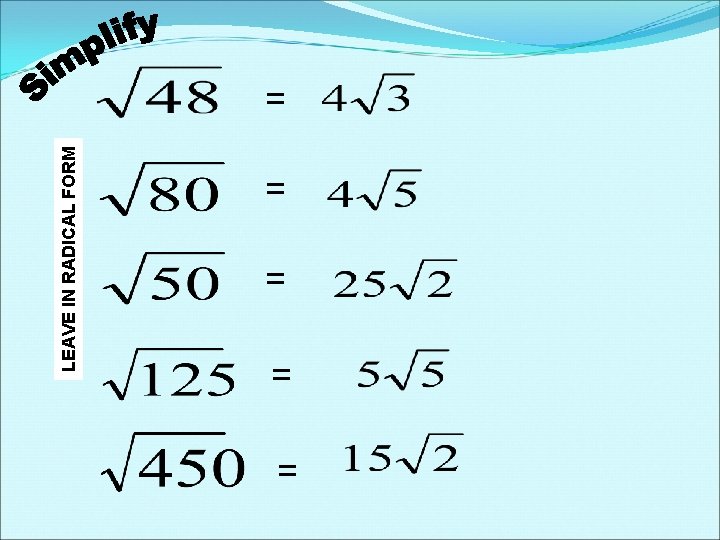
LEAVE IN RADICAL FORM = = =

Adding or Subtracting Radicals To add or subtract square roots you must have like radicands (the number under the radical). Then you add or subtract the coefficients! Sometimes you must simplify first:

Example 1:

Try These
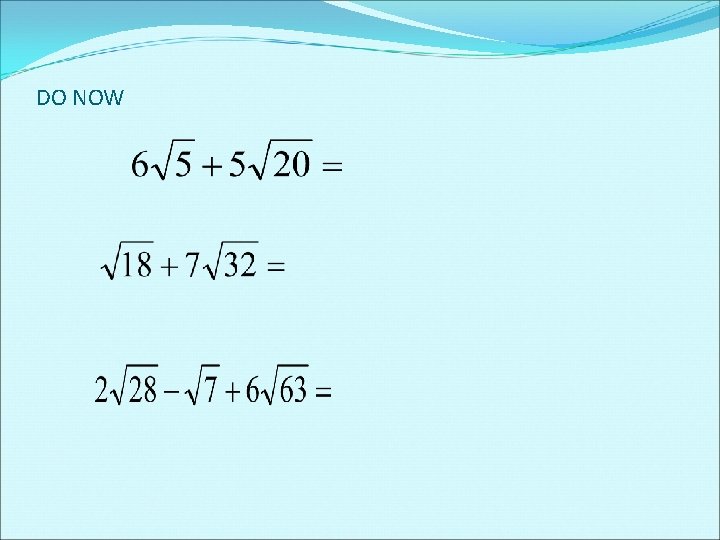
DO NOW

* To multiply radicals: multiply the coefficients and then multiply the radicands and then simplify the remaining radicals.

Radical Product Property ONLY when a≥ 0 and b≥ 0 For Example: Equal
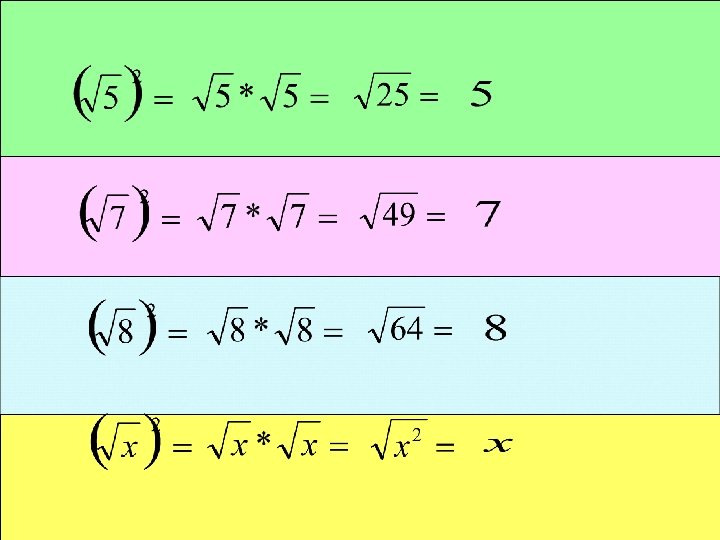

Multiplying Radicals 1. Multiply terms outside the radical together. 2. Multiply terms inside the radical together. 3. Simplify.

Multiplication and Radicals Simplify the expression:

Multiply then simplify

Multiplying Radicals You can multiply using distributive property and FOIL.

Multiply: You try.

Using the Conjugate to Simplify Conjugate Expression Conjugate Product The radical “goes away” every time

To divide radicals: divide the coefficients, divide the radicands if possible, and rationalize the denominator so that no radical remains in the denominator

Radical Quotient Property ONLY when a≥ 0 and b≥ 0 For Example: Equal
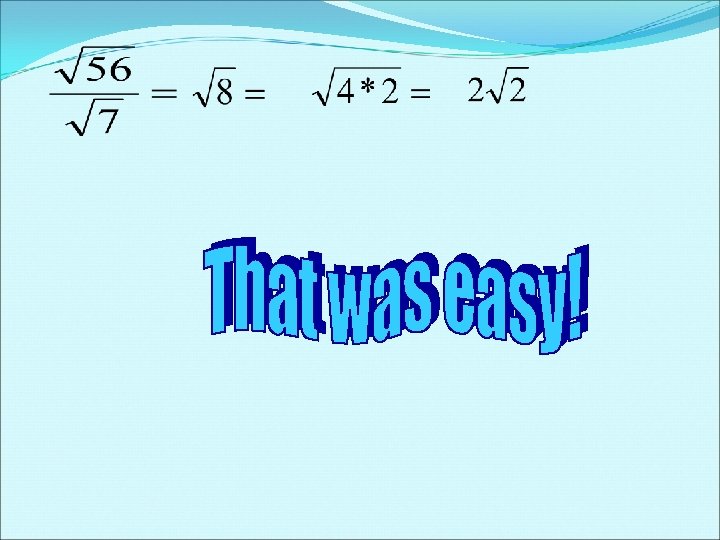

Fractions and Radicals Simplify the expressions: There is nothing to simplify because the square root is simplified and every term in the fraction can not be divided by 10. Make sure to simplify the fraction.

Dividing to Simplify Radicals No radicals in the denominator allowed Denominators must be “rationalized. ” Multiply by 1 √ in the form of 3 1 √

Using the Conjugate to Simplify Conjugate Expression Conjugate Product The radical “goes away” every time

Dividing to Simplify Radicals Multiply by 5 1 11 1 conjugate in the form of conjugate
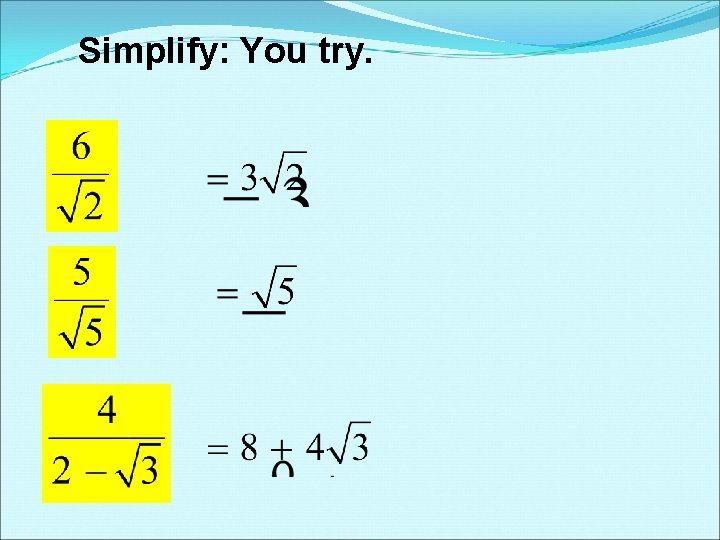
Simplify: You try.

This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator. 42 cannot be simplified, so we are finished.

This can be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator.

This cannot be divided which leaves the radical in the denominator. We do not leave radicals in the denominator. So we need to rationalize by multiplying the fraction by something so we can eliminate the radical in the denominator. Reduce the fraction.

Summary: To ADD and SUBTRACT To MULTIPLY COMBINE LIKE TERMS “Outside” NUMBERS x NUMBERS “Inside” NUMBERS x NUMBERS DISTRIBUTE and FOIL To DIVIDE “Rationalize” denominator using Use conjugate ALWAYS SIMPLIFY AT THE END IF YOU CAN 1