RADICAL FUNCTIONS AND RATIONAL EXPONENTS Chapter 6 6

RADICAL FUNCTIONS AND RATIONAL EXPONENTS Chapter 6

6. 1 ROOTS AND RADICAL EXPRESSIONS Pg. 361 -366 Obj: Learn how to find nth roots. A. SSE. 2

6. 1 ROOTS AND RADICAL EXPRESSIONS The nth Root If aⁿ = b, with a and b real numbers and n a positive integer, then a is an nth root of b. If n is odd There is one real nth root of b, denoted in radical form as If n is even And b is positive, there are two real nth roots of b. The positive root is the principal root and its symbol is. The negative root is its opposite. And b is negative, there are no real nth roots of b. The only nth root of 0 is O.

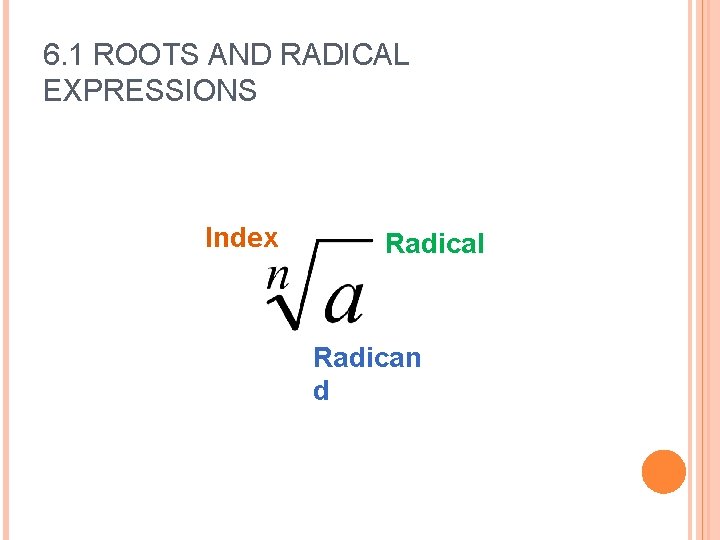
6. 1 ROOTS AND RADICAL EXPRESSIONS Index Radical Radican d

6. 1 ROOTS AND RADICAL EXPRESSIONS nth Roots of nth Powers For any real numbers a, a if n is odd |a| if n is even

6. 2 MULTIPLYING AND DIVIDING RADICAL EXPRESSIONS Pg. 367 -373 Obj: Learn how to multiply and divide radical expressions. A. SSE. 2

6. 2 MULTIPLYING AND DIVIDING RADICAL EXPRESSIONS Combining Radical Expressions: Products Simplest Form – a radical that is reduced as much as possible Combining Radical Expressions: Quotients

6. 2 MULTIPLYING AND DIVIDING RADICAL EXPRESSIONS Rationalize the Denominator – rewrite the expression so that there are no radicals in any denominator and no denominator in any radical

6. 3 BINOMIAL RADICAL EXPRESSIONS Pg. 374 -380 Obj: Learn how to add and subtract radical expressions. A. SSE. 2

6. 3 BINOMIAL RADICAL EXPRESSIONS Like Radicals – radical expressions that have the same index and radicand Combining Radical Expressions: Sums and Differences

6. 4 RATIONAL EXPONENTS Pg. 381 – 388 Obj: Learn how to simplify expressions with rational exponents. N. RN. 2, N. RN. 1

6. 4 RATIONAL EXPONENTS Rational Exponent Properties of Rational Exponents

6. 5 SOLVING SQUARE ROOT AND OTHER RADICAL EQUATIONS Pg. 390 -397 Obj: Learn how to solve square root and other radical equations. A. REI. 2, A. CED. 4

6. 5 SOLVING SQUARE ROOT AND OTHER RADICAL EQUATIONS Radical Equation – an equation that has a variable in a radicand or a variable with a rational exponent Square Root Equation – a radical equation that has an index of 2

6. 6 FUNCTION OPERATIONS Pg. 398 -404 Obj: Learn how to add, subtract, multiply, and divide functions and to find the composite of two functions. F. BF. 1. b, F. BF. 1. c

6. 6 FUNCTION OPERATIONS Function Operations (f+g)(x) = f(x) + g(x) (f-g)(x) = f(x) – g(x) (f∙g)(x) = f(x) ∙ g(x) (f/g)(x) = f(x)/g(x), g(x)≠ 0 Composition of Functions Evaluate f(x) first Then use f(x) as the input for g

6. 7 INVERSE RELATIONS AND FUNCTIONS Pg. 405 – 412 Obj: Learn how to find the inverse of a relation or function. F. BF. 4. a, F. BF. 4. c

6. 7 INVERSE RELATIONS AND FUNCTIONS Inverse Relation If a relation pairs element a of its domain to element b of its range, the inverse relation pairs b with a. If (a, b) is an ordered pair of a relation, then (b, a) is an ordered pair of its inverse. Inverse Functions – when both the relation and its inverse are functions One-to-one Function – each y-value in the range corresponds to exactly one x-value in the domain

6. 7 INVERSE RELATIONS AND FUNCTIONS Composition of Inverse Functions

6. 8 GRAPHING RADICAL FUNCTIONS Pg. 414 – 420 Obj: Learn how to graph square root and other radical functions. F. IF. 7. b, F. IF. 8

6. 8 GRAPHING RADICAL FUNCTIONS Families of Radical Functions Parent Function Reflection Stretch in x-axis (a > 1) or Shrink (0 < a < 1) Translation: Horizontal by h; Vertical by k