Polynomial Long Division and Synthetic Division What You































- Slides: 32

Polynomial Long Division and Synthetic Division

What You Should Learn • Use long division to divide polynomials by other polynomials. • Use synthetic division to divide polynomials by binomials of the form (x – k). • Use the Remainder Theorem and the Factor Theorem.

When our factoring techniques do not easily work… n Analyzing and Graphing a Function Let’s say we want to analyze this function and graph it: f(x) = x 7 - 8 x 5 - 2 x 4 - 21 x 3 + 10 x 2 + 108 x + 72 ¨ We know the left and right behavior ¨ We know the y- intercept ¨ To get a good approximation of the graph, we need to know the x -intercepts or the “zeros”. To find all the real zeros of the function we must factor it completely. ¨ n n Determining if one polynomial is a factor of another polynomial Factoring a polynomial Polynomial division will help with this.

Today We are going to learn about the process of division n Learn about a couple of theorems to help in factoring and solving higher level polynomials n

Division of Polynomials n In this section, we will study two procedures for dividing polynomials. n These procedures are especially valuable in factoring and finding the zeros of polynomial functions.

Polynomial Division n Polynomial Division is very similar to long division. n Example:

Polynomial Division Subtract!!

Polynomial Division n Example: n Notice that there is no x term. However, we need to include it when we divide.

Polynomial Division

Try This n Example: n Answer:

Now let’s look at another method to divide… Why? ? ? n Sometimes it is easier… n

Synthetic Division is a ‘shortcut’ for polynomial division that only works when dividing by a linear factor (x + b). n It involves the coefficients of the dividend, and the zero of the divisor. n

Example § Divide: § Step 1: § Write the coefficients of the dividend in a upside-down division symbol. 1 5 6

Example § Step 2: § Take the zero of the divisor, and write it on the left. § The divisor is x – 1, so the zero is 1. 1 1 5 6

Example § Step 3: § Carry down the first coefficient. 1 1 1 5 6

Example § Step 4: § Multiply the zero by this number. Write the product under the next coefficient. 1 1 1 5 1 6

Example § Step 5: § Add. 1 1 5 1 1 6 6

Example § Step etc. : § Repeat as necessary 1 1 1 5 1 6 6 6 12

Example The numbers at the bottom represent the coefficients of the answer. The new polynomial will be one degree less than the original. 1 1 1 5 1 6 6 6 12

Synthetic Division The pattern for synthetic division of a cubic polynomial is summarized as follows. (The pattern for higher-degree polynomials is similar. )

Synthetic Division This algorithm for synthetic division works only for divisors of the form x – k. Remember that x + k = x – (–k).

Using Synthetic Division Use synthetic division to divide x 4 – 10 x 2 – 2 x + 4 by x + 3. Solution: You should set up the array as follows. Note that a zero is included for the missing x 3 -term in the dividend.

Example – Solution cont’d n Then, use the synthetic division pattern by adding terms in columns and multiplying the results by – 3. n So, you have n .

Try These n Examples: + x 3 – 11 x 2 – 5 x + 30) (x – 2) ¨ (x 4 – 1) (x + 1) [Don’t forget to include the missing terms!] ¨ (x 4 n Answers: ¨ x 3 + 3 x 2 – 5 x – 15 ¨ x 3 – x 2 + x – 1

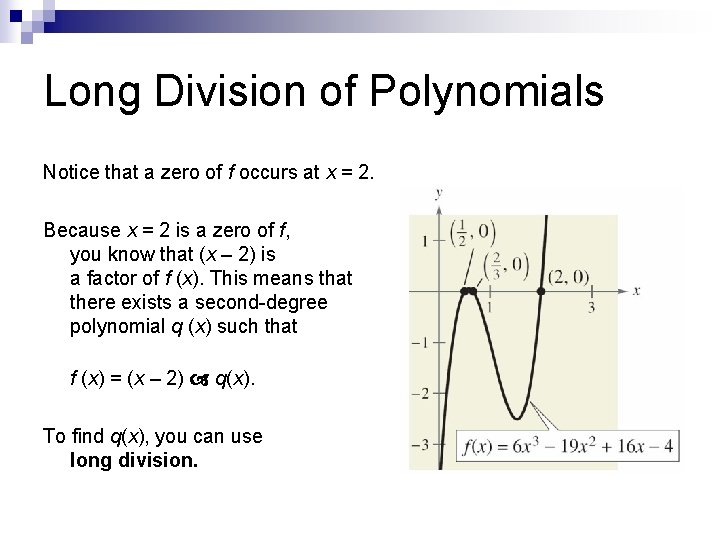
Application of Long Division To begin, suppose you are given the graph of f (x) = 6 x 3 – 19 x 2 + 16 x – 4.

Long Division of Polynomials Notice that a zero of f occurs at x = 2. Because x = 2 is a zero of f, you know that (x – 2) is a factor of f (x). This means that there exists a second-degree polynomial q (x) such that f (x) = (x – 2) q(x). To find q(x), you can use long division.

Example - Long Division of Polynomials Divide 6 x 3 – 19 x 2 + 16 x – 4 by x – 2, and use the result to factor the polynomial completely.

Example 1 – Solution Think Multiply: 6 x 2(x – 2). Subtract. Multiply: – 7 x(x – 2). Subtract. Multiply: 2(x – 2). Subtract.

Example – Solution From this division, you can conclude that 6 x 3 – 19 x 2 + 16 x – 4 = (x – 2)(6 x 2 – 7 x + 2) and by factoring the quadratic 6 x 2 – 7 x + 2, you have 6 x 3 – 19 x 2 + 16 x – 4 = (x – 2)(2 x – 1)(3 x – 2). cont’d

Long Division of Polynomials

Example – Factoring a Polynomial: Repeated Division Show that (x – 2) and (x + 3) are factors of f (x) = 2 x 4 + 7 x 3 – 4 x 2 – 27 x – 18. Then find the remaining factors of f (x). Solution: Using synthetic division with the factor (x – 2), you obtain the following. 0 remainder, so f (2) = 0 and (x – 2) is a factor.

Example – Solution cont’d Take the result of this division and perform synthetic division again using the factor (x + 3). 0 remainder, so f (– 3) = 0 and (x + 3) is a factor. Because the resulting quadratic expression factors as 2 x 2 + 5 x + 3 = (2 x + 3)(x + 1) the complete factorization of f (x) is f (x) = (x – 2)(x + 3)(2 x + 3)(x + 1).