Section 5 2 Properties of Rational Functions Defn

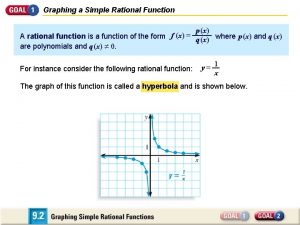
Section 5. 2 – Properties of Rational Functions Defn: Rational Function The functions p and q are polynomials. The domain of a rational function is the set of all real numbers except those values that make the denominator, q(x), equal to zero.

Section 5. 2 – Properties of Rational Functions Domain of a Rational Function {x | x – 4} or (- , -4) (-4, )

graph

Section 5. 2 – Properties of Rational Functions Domain of a Rational Function {x | x 2} or (- , 2) (2, )

graph

Section 5. 2 – Properties of Rational Functions Domain of a Rational Function {x | x – 3, 3} or (- , -3) (-3, 3) (3, )

graph

Section 5. 2 – Properties of Rational Functions Domain of a Rational Function {x | x – 3, 5} or (- , -3) (-3, 5) (5, )

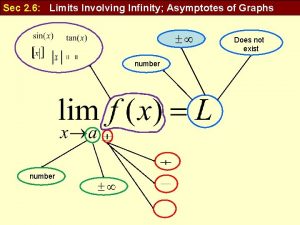
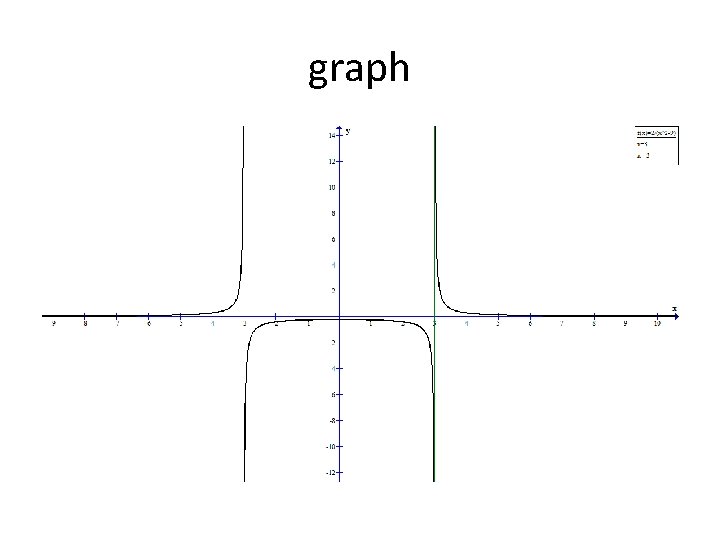
Section 5. 2 – Properties of Rational Functions Linear Asymptotes (vertical, horizontal, or oblique) Lines in which a graph of a function will approach. By approach we mean each successive value of X puts the graph closer to the asymptote than the previous value. Vertical Asymptote A vertical asymptote exists for any value of x that makes the denominator zero AND is not a value that makes the numerator zero, in this case the factors would cancel. Example A vertical asymptotes exists at x = -5.

graph

Section 5. 2 – Properties of Rational Functions Asymptotes Vertical Asymptote Example A vertical asymptote does not exist at x = 3 as it is a value that also makes the numerator zero. A hole exists in the graph at x = 3.

graph

Section 5. 2 – Properties of Rational Functions Asymptotes Horizontal Asymptote A horizontal asymptote exists if the largest exponents in the numerator and the denominator are equal, or if the largest exponent in the denominator is larger than the largest exponent in the numerator. If the largest exponent in the denominator is equal to the largest exponent in the numerator, then the horizontal asymptote is equal to the ratio of the coefficients.

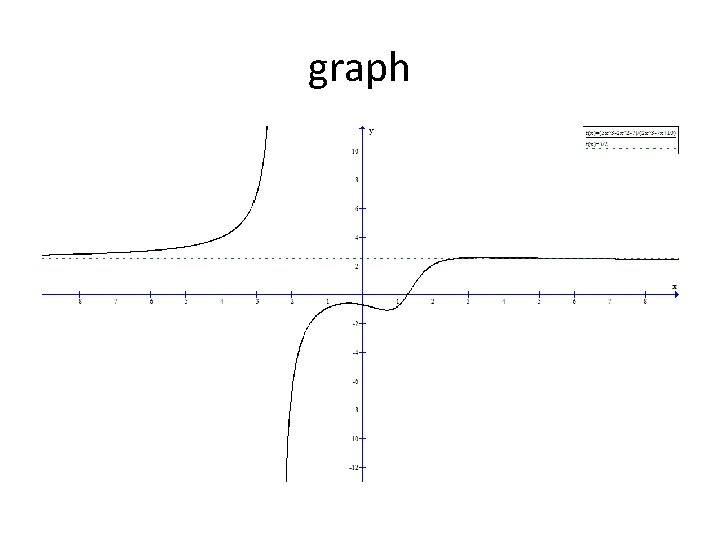
Section 5. 2 – Properties of Rational Functions Asymptotes Horizontal Asymptote Example A horizontal asymptote exists at y = 5/2. A horizontal asymptote exists at y = 0.

graph

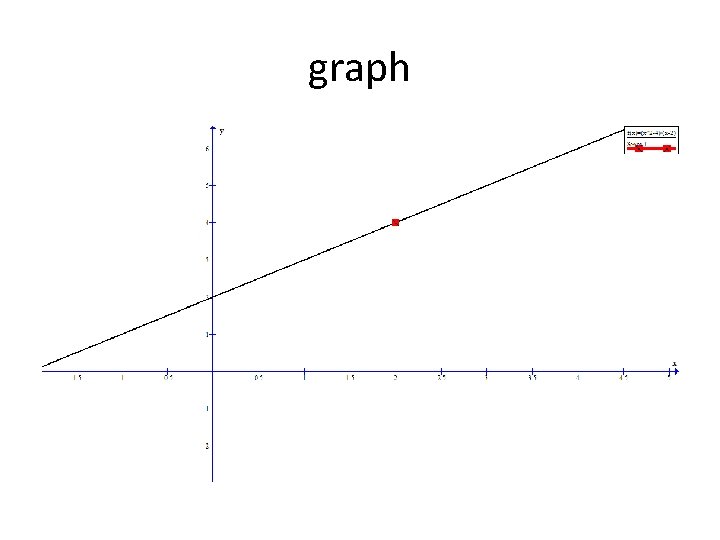
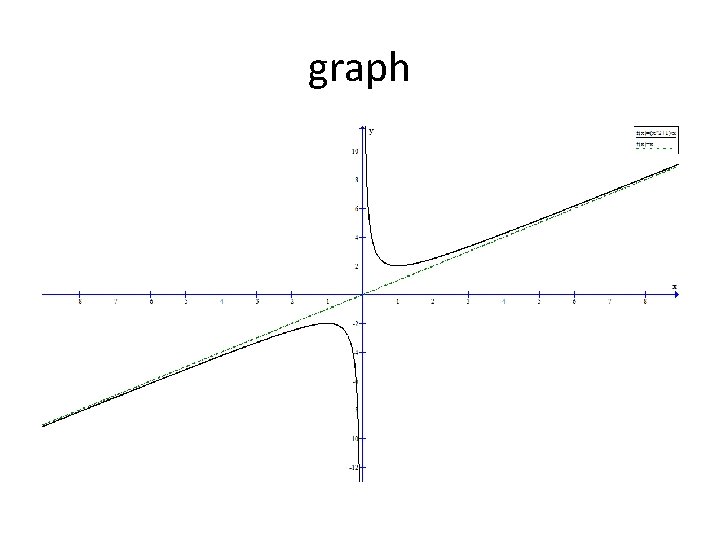
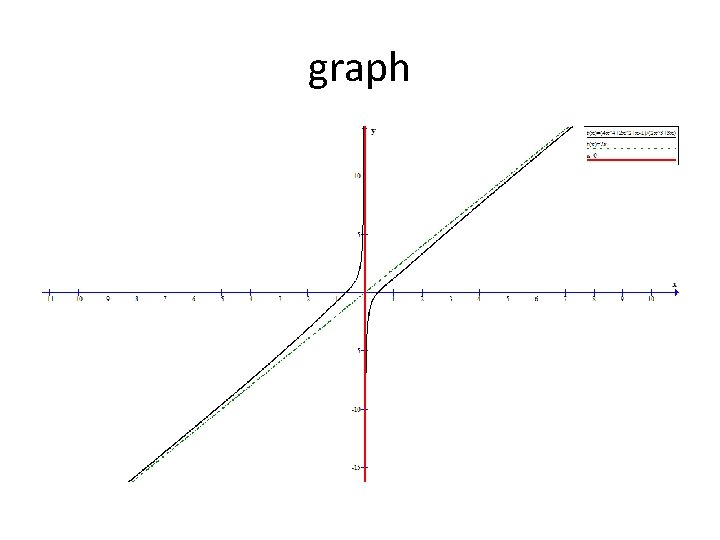
Section 5. 2 – Properties of Rational Functions Asymptotes Oblique (slant) Asymptote An oblique asymptote exists if the largest exponent in the numerator is one degree larger than the largest exponent in the denominator. **Note** Other non-linear asymptotes can exist for a rational function.

Section 5. 2 – Properties of Rational Functions Asymptotes Oblique Asymptote Example An oblique asymptote exists. Long division is required. We ignore the remainder if it exists

graph

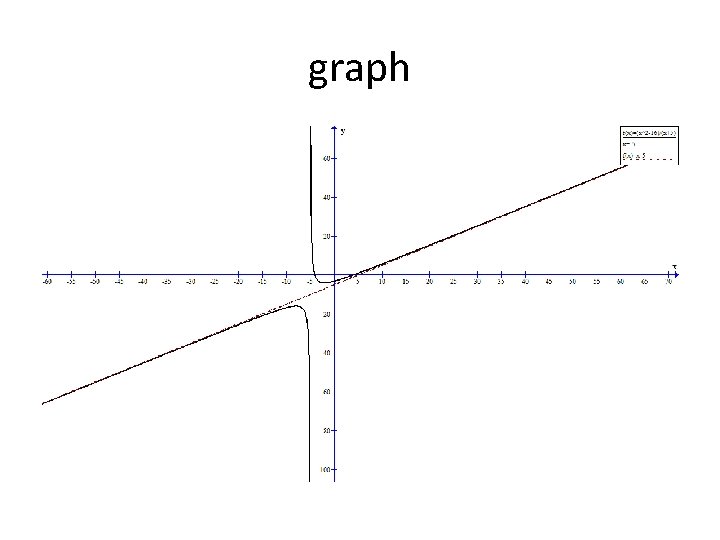
Section 5. 2 – Properties of Rational Functions Asymptotes Oblique Asymptote Example An oblique asymptote exists. Long division is required. An oblique asymptote exists at y = 2 x

graph