Unit 2 Fonction Quadratique et quations Lesson 1

Unité 2: Fonction Quadratique et Équations Lesson 1 Introduction au fonction Quadratiques

Une fonction quadratique à la forme 2 y = ax + bx + c, ou a, b et c des nombres avec a non nul. Le graphe (la courbe) d’une fonction quadratique y = ax 2 + bx + c représente tous les points (x, y) qui satisfont à la fonction.

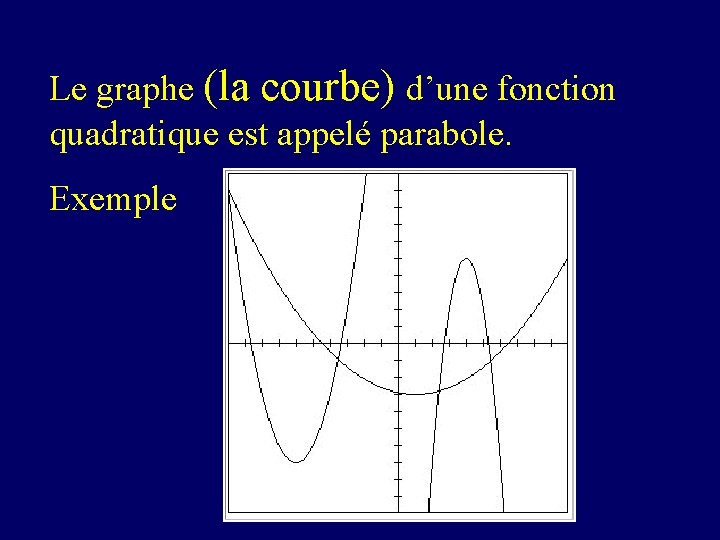
Le graphe (la courbe) d’une fonction quadratique est appelé parabole. Exemple

Toute parabole a un axe de symétrie. La parabole intersecte son axe de symétrie en un point appelé Sommet de la parabole.

Nous avons déja vu que deux points différents déterminent une doite unique. Un résultat similaire pour les paraboles. Étant donné trois points dans le plan ayant des abscisse différents et non alignés, Il existe une et une seule parabole passant par ces 3 points.

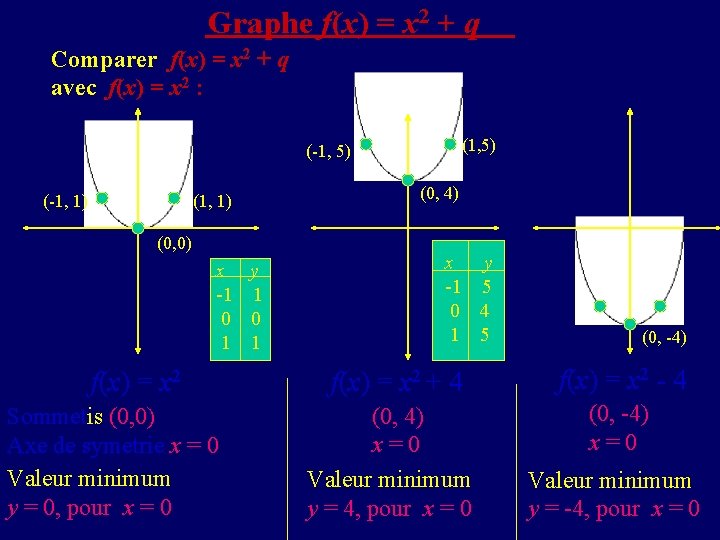
Graphe f(x) = x 2 + q Comparer f(x) = x 2 + q avec f(x) = x 2 : (1, 5) (-1, 1) (0, 0) x y -1 1 0 0 1 1 f(x) = x 2 Sommetis (0, 0) Axe de symetrie x = 0 Valeur minimum y = 0, pour x = 0 (0, 4) x y -1 5 0 4 1 5 f(x) = x 2 + 4 (0, 4) x=0 Valeur minimum y = 4, pour x = 0 (0, -4) f(x) = x 2 - 4 (0, -4) x=0 Valeur minimum y = -4, pour x = 0

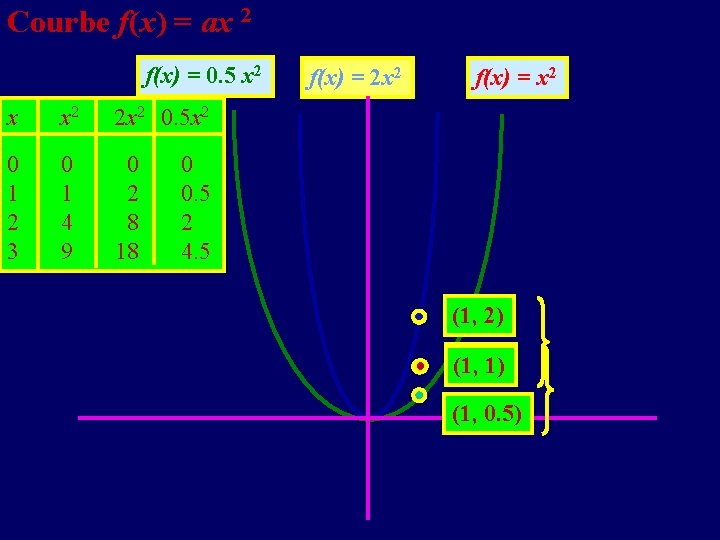
Courbe f(x) = ax 2 f(x) = 0. 5 x 2 f(x) = 2 x 2 f(x) = x 2 2 x x x 2 x 22 x 0. 5 x 2 0 1 2 3 00 1 14 49 9 00 2 28 818 18 0 0. 5 2 4. 5 (1, 2) (1, 1) (1, 0. 5)

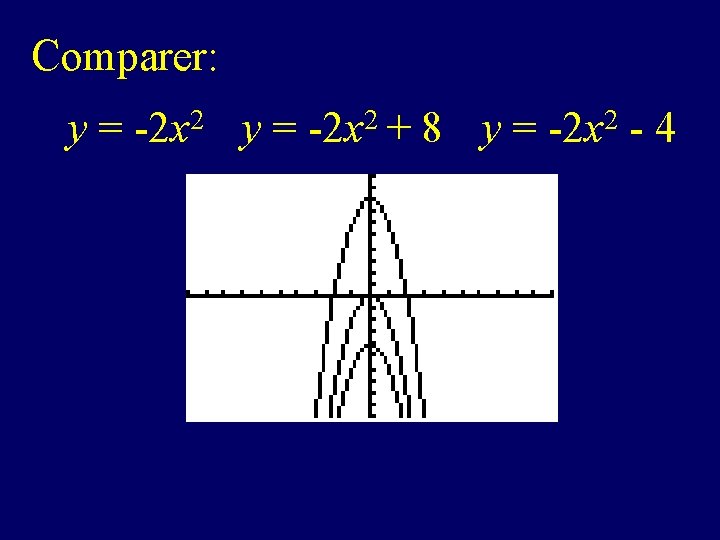
Comparer: y = -2 x 2 + 8 y = -2 x 2 - 4

y = ax 2 + q: a détérmines l’ouverture de la parabole. Si a > 0, ouverture vert le haut up Si a < 0, ouverture vert le bas

y = ax 2 + q: q determines la translation verticale de la parabole. Si q > 0, déplacer vers le haut Si q < 0, déplacer vers le bas

La parabole avec un sommet (0, -2) passant par le point (3, 1). Trouver l’équation de la parabole the forme y = ax 2 + q.

Les solutions de l’équation ax 2 + bx + c = 0 sont appelés les zéros de la fonction quadratique f(x) = ax 2 + bx + c.

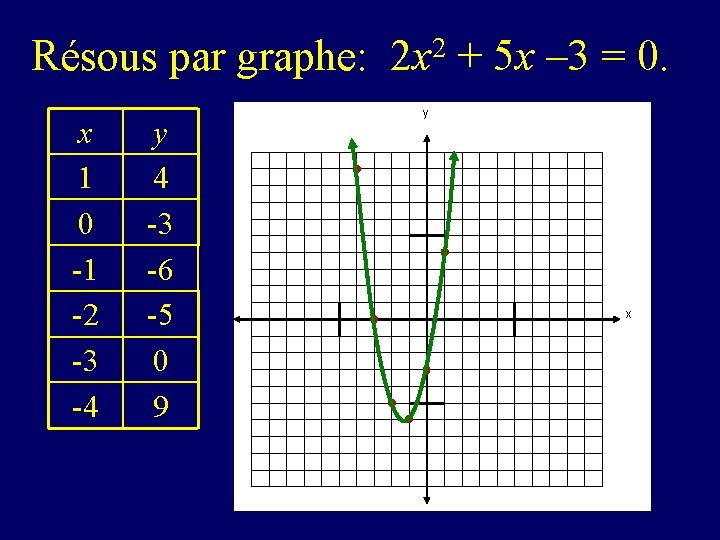
Résous par graphe: 2 x 2 + 5 x – 3 = 0. x 1 0 -1 -2 -3 -4 y 4 -3 -6 -5 0 9 y x

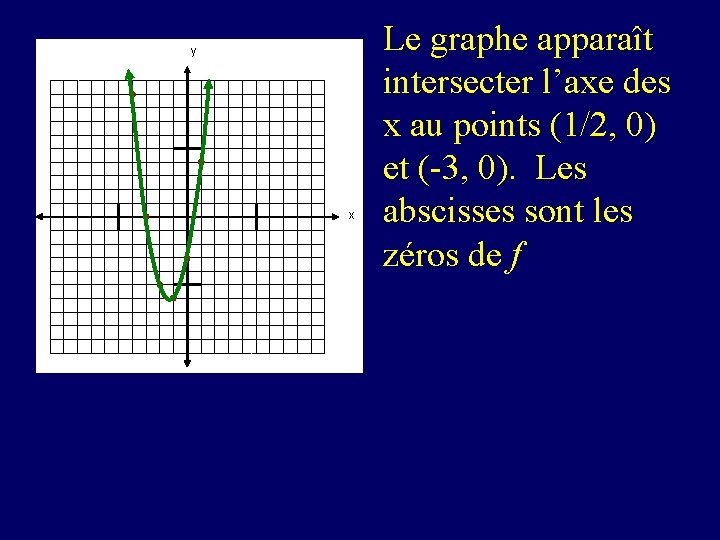
y x Le graphe apparaît intersecter l’axe des x au points (1/2, 0) et (-3, 0). Les abscisses sont les zéros de f

Vérifions que ½ et – 3 sont les zéros de f. (1/2, 0) (-3, 0)

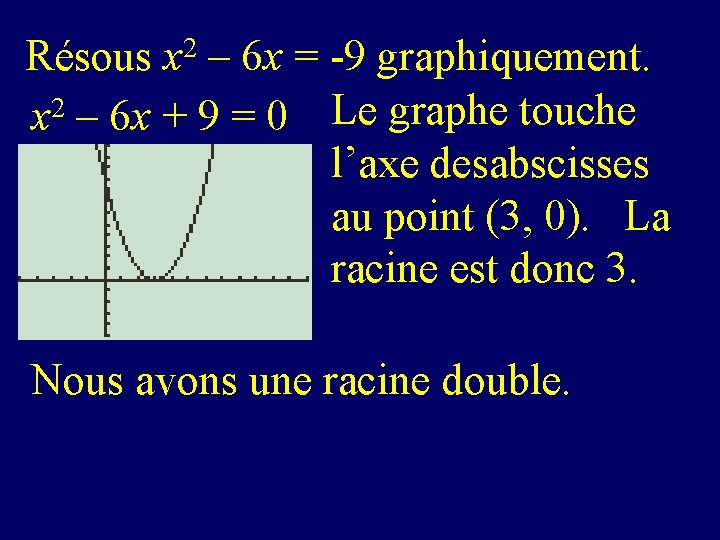
Résous x 2 – 6 x = -9 graphiquement. x 2 – 6 x + 9 = 0 Le graphe touche l’axe desabscisses au point (3, 0). La racine est donc 3. Nous avons une racine double.

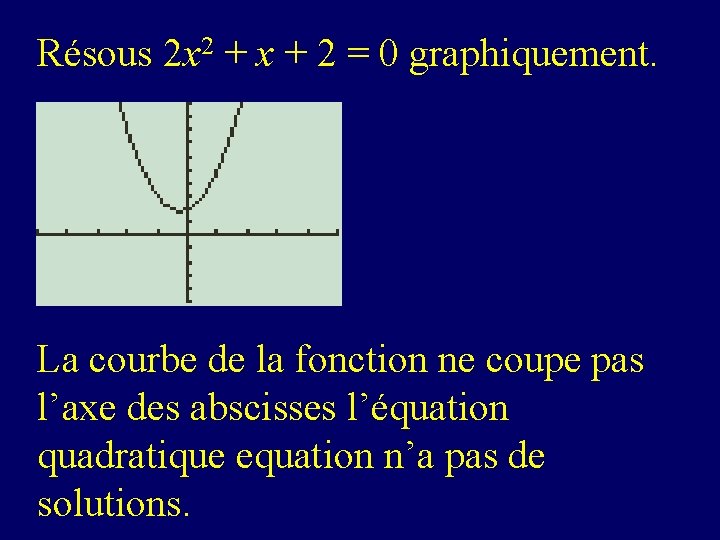
Résous 2 x 2 + x + 2 = 0 graphiquement. La courbe de la fonction ne coupe pas l’axe des abscisses l’équation quadratique equation n’a pas de solutions.

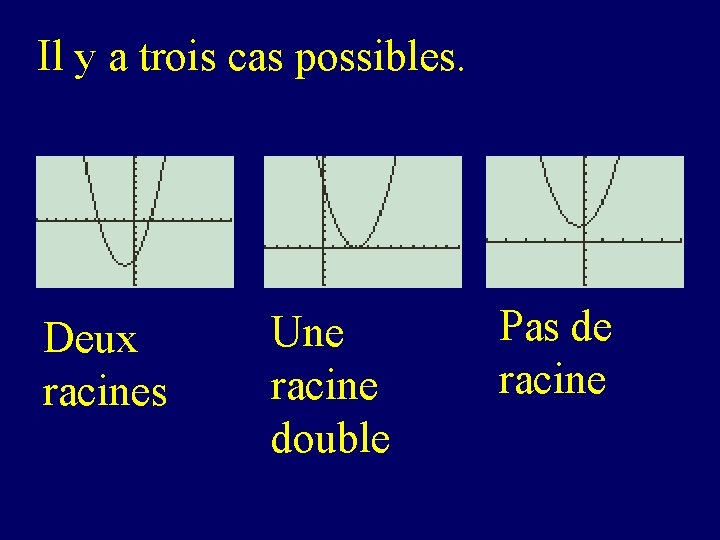
Il y a trois cas possibles. Deux racines Une racine double Pas de racine

Devoir: p. 155 #1, 5, 7, 11, 15, 18, 19, 21, 33, 34, 38

• Utiliser ti 83 pour trouver la relation entre • Y=ax 2 Et • Y=a(x-p)2 • Congruence • Feuille de travaille p 59