La fonction RATIONNELLE quations et graphique fx 1

La fonction RATIONNELLE

Équations et graphique f(x) = 1 (forme générale de BASE) x a b (x – h) a x–h + k (forme générale TRANSFORMÉE) + k (forme CANONIQUE) Polynôme 1 Polynôme 2 (forme P / Q) Exemple : f(x) = 3 x – 4 2 x + 5

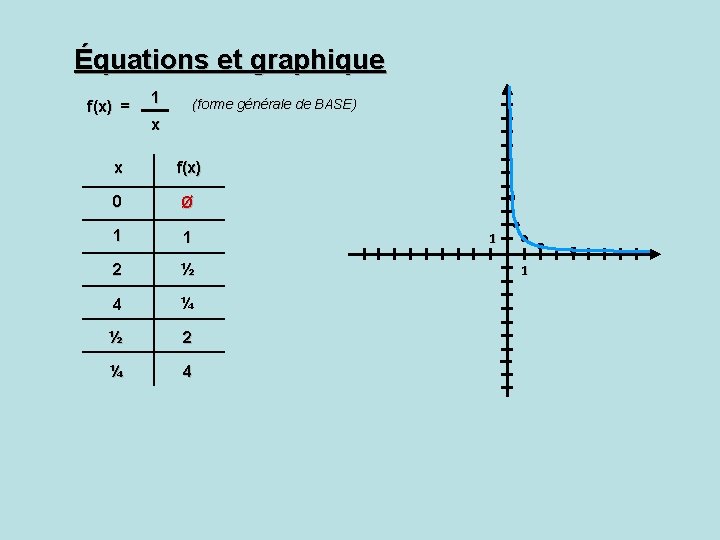
Équations et graphique f(x) = 1 (forme générale de BASE) x x f(x) 0 Ø 1 1 2 ½ 4 ¼ ½ 2 ¼ 4 1 1

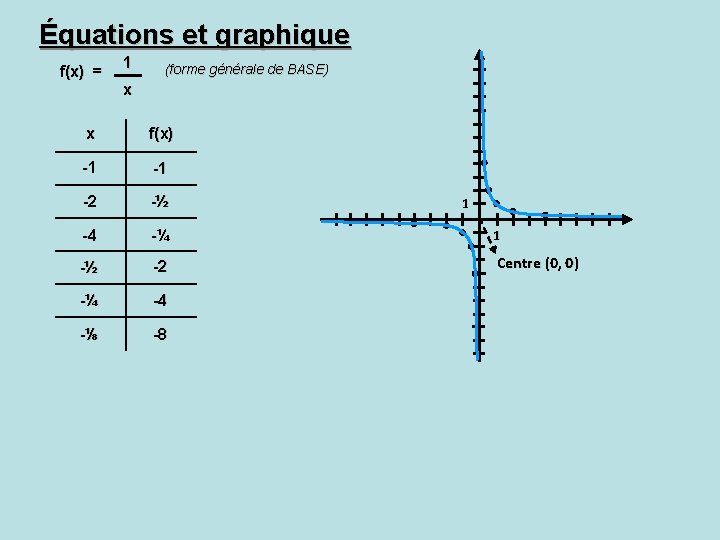
Équations et graphique f(x) = 1 (forme générale de BASE) x x f(x) -1 -1 -2 -½ -4 -¼ 1 -½ -2 Centre (0, 0) -¼ -4 -⅛ -8 1

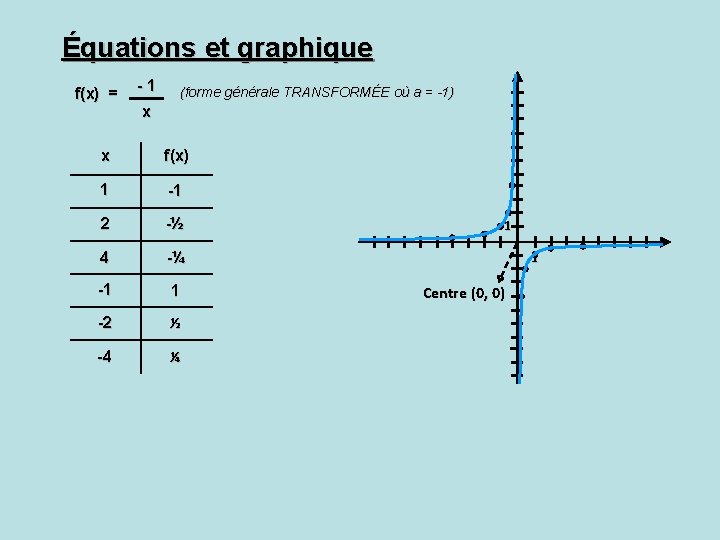
Équations et graphique f(x) = -1 (forme générale TRANSFORMÉE où a = -1) x x f(x) 1 -1 2 -½ 4 -¼ -1 1 -2 ½ -4 ¼ 1 1 Centre (0, 0)

Équations et graphique f(x) = 1 (forme générale TRANSFORMÉE où b = -1) -x x f(x) 1 -1 2 -½ 4 -¼ -1 1 -2 ½ -4 ¼ 1 1 Centre (0, 0)

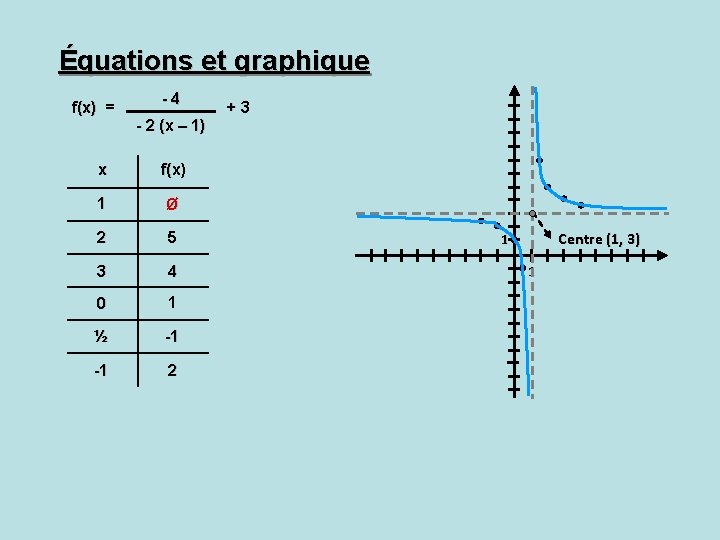
Équations et graphique f(x) = -4 - 2 (x – 1) x f(x) 1 Ø 2 5 3 4 0 1 ½ -1 -1 2 +3 Centre (1, 3) 1 1

Équations et graphique f(x) = a b (x – h) + k (h, k) = centre x = h y = k Équations des asymptotes Asymptotes y = k Centre (h, k) 1 1 x = h Dom f = {h} Ima f = {k} (forme générale TRANSFORMÉE)

Recherche de l’équation Exemple : Trouver l’équation dont les deux asymptotes du graphique ont pour équation x = 3 et y = 5 et dont le point (-1, 2) appartient au graphique.

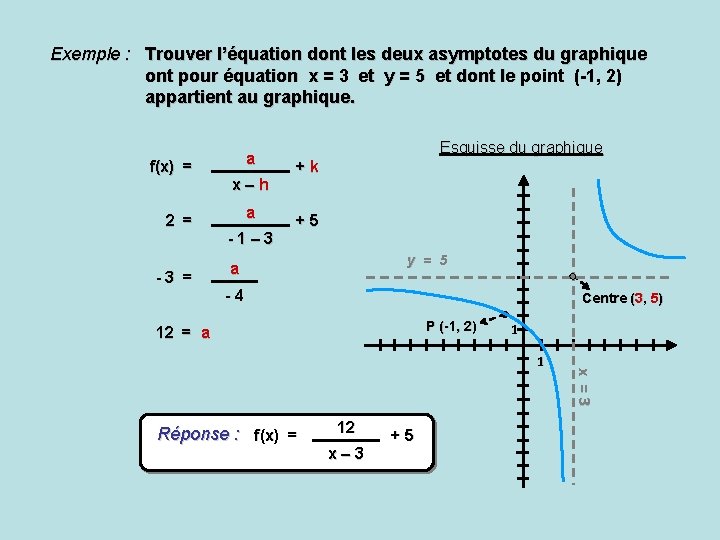
Exemple : Trouver l’équation dont les deux asymptotes du graphique ont pour équation x = 3 et y = 5 et dont le point (-1, 2) appartient au graphique. f(x) = 2 = -3 = a x–h a -1– 3 Esquisse du graphique +k +5 y = 5 a -4 Centre (3, 5) P (-1, 2) 12 = a 1 Réponse : f(x) = 12 x– 3 +5 x =3 1

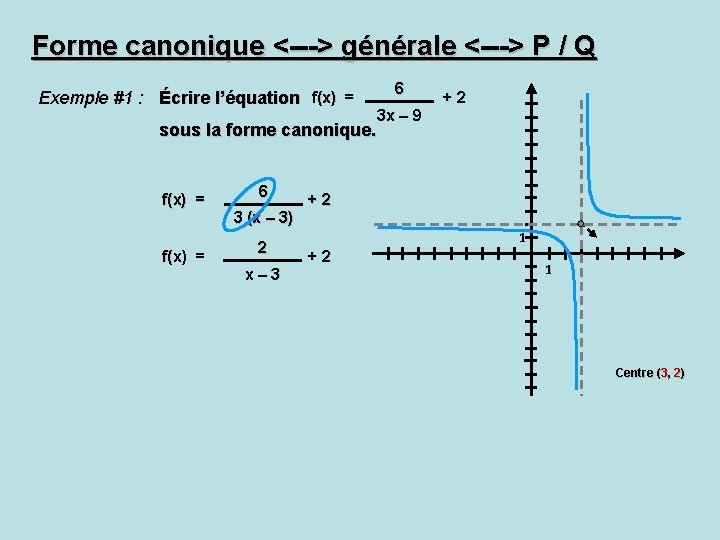
Forme canonique <---> générale <---> P / Q Exemple #1 : Écrire l’équation f(x) = sous la forme canonique. f(x) = 6 3 (x – 3) 2 x– 3 6 3 x – 9 +2 +2 1 Centre (3 (3, 2)

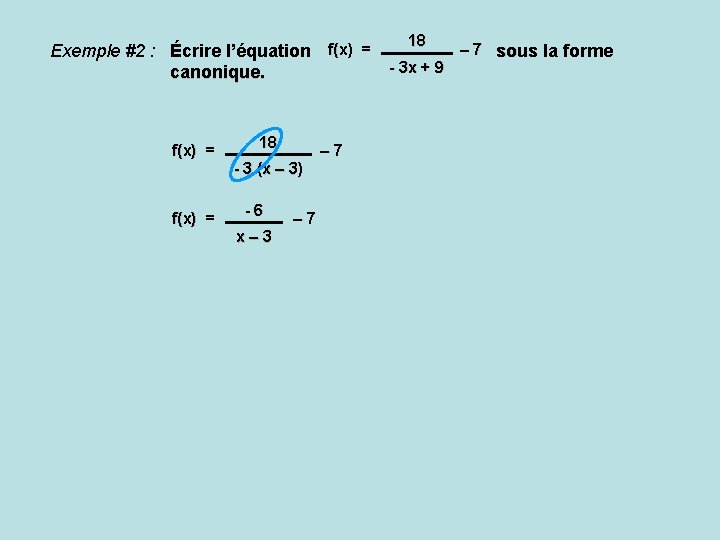
18 – 7 sous la forme Exemple #2 : Écrire l’équation f(x) = - 3 x + 9 canonique. f(x) = 18 - 3 (x – 3) -6 x– 3 – 7

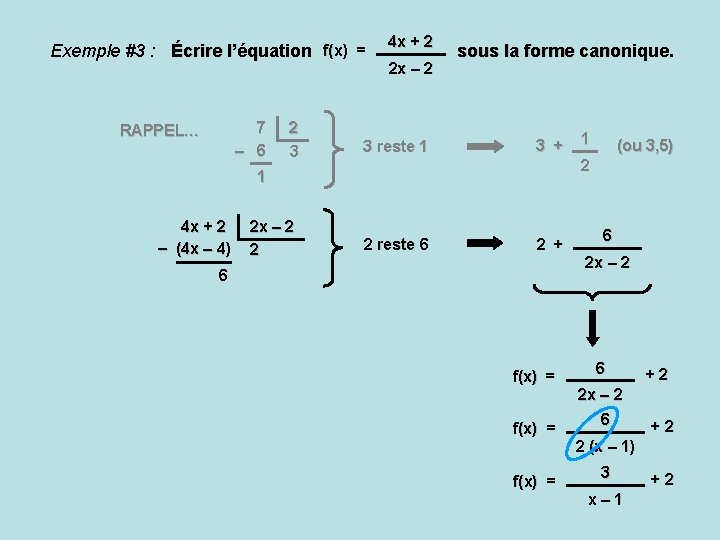
Exemple #3 : Écrire l’équation f(x) = 7 – 6 RAPPEL… 4 x + 2 2 x – 2 2 3 3 reste 1 2 x – 2 2 2 reste 6 sous la forme canonique. 3 + (ou 3, 5) 2 1 4 x + 2 – (4 x – 4) 1 2 + 6 f(x) = 6 2 x – 2 6 +2 2 (x – 1) 3 x– 1 +2

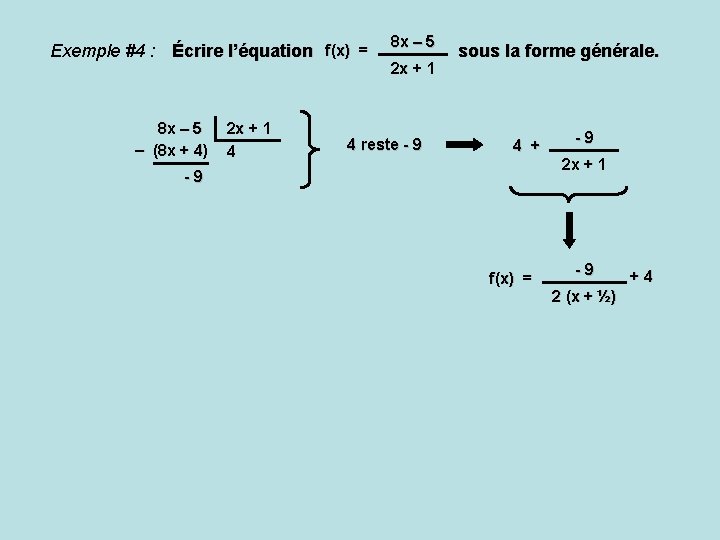
Exemple #4 : Écrire l’équation f(x) = 8 x – 5 – (8 x + 4) 2 x + 1 4 8 x – 5 2 x + 1 4 reste - 9 sous la forme générale. 4 + -9 f(x) = -9 2 x + 1 -9 2 (x + ½) +4

Exemple #5 : Écrire l’équation f(x) = f(x) = 2 3 x + 3 2 3 (x + 1) – 4 (3 x + 3) – 12 x + 12 3 x + 3 2 – (12 x + 12) 3 x + 3 2 – 12 x – 12 3 x + 3 - 12 x – 10 3 x + 3 – 4 sous la forme P / Q. Mettre les termes sur le même dénominateur !

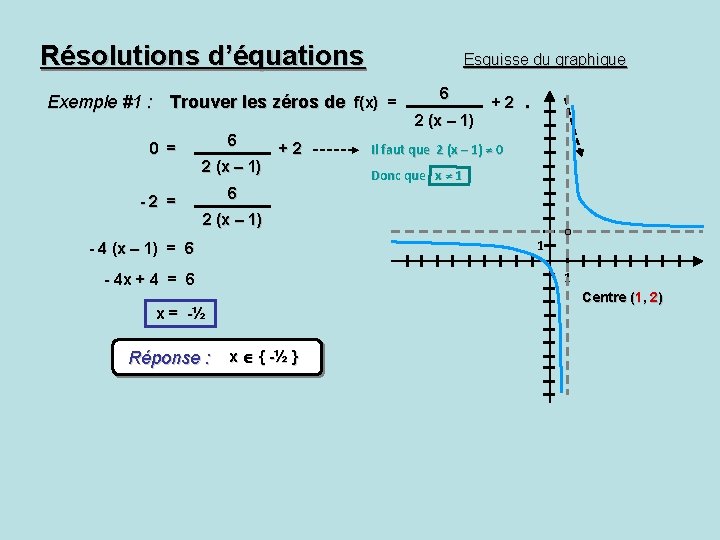
Résolutions d’équations Esquisse du graphique Exemple #1 : Trouver les zéros de f(x) = 0 = -2 = 6 2 (x – 1) +2. Il faut que 2 (x – 1) ≠ 0 Donc que x ≠ 1 6 2 (x – 1) 1 - 4 (x – 1) = 6 1 - 4 x + 4 = 6 Centre (1, 2) x = -½ Réponse : x { -½ }

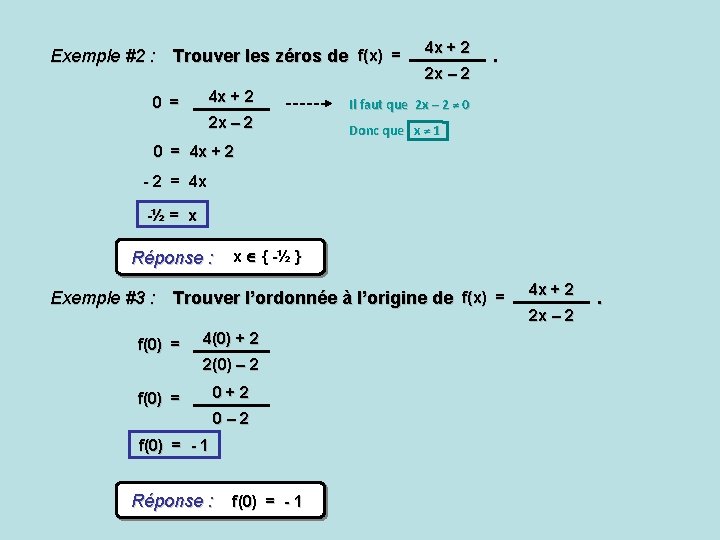
Exemple #2 : Trouver les zéros de f(x) = 4 x + 2 0 = 2 x – 2 4 x + 2 2 x – 2 . Il faut que 2 x – 2 ≠ 0 Donc que x ≠ 1 0 = 4 x + 2 - 2 = 4 x -½ = x Réponse : x { -½ } Exemple #3 : Trouver l’ordonnée à l’origine de f(x) = f(0) = 4(0) + 2 2(0) – 2 f(0) = 0+2 0– 2 f(0) = - 1 Réponse : f(0) = - 1 4 x + 2 2 x – 2 .

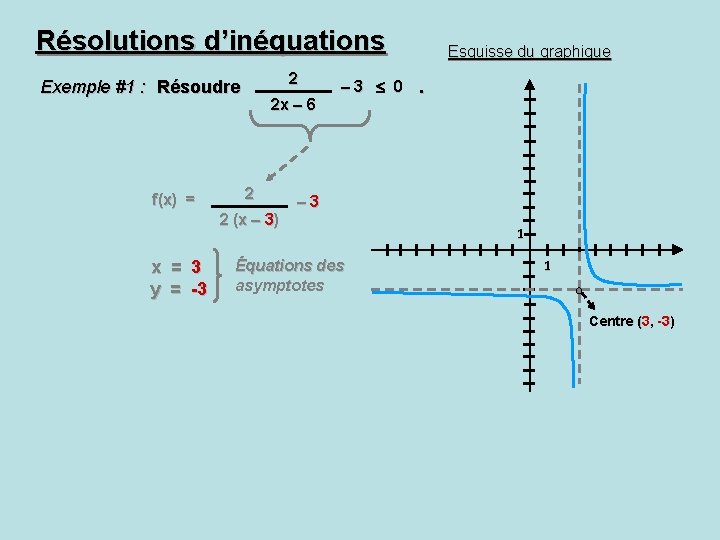
Résolutions d’inéquations 2 Exemple #1 : Résoudre f(x) = 2 x – 6 2 2 (x – 3) x = 3 y = -3 – 3 0 Esquisse du graphique . – 3 Équations des asymptotes 1 1 Centre (3, -3)

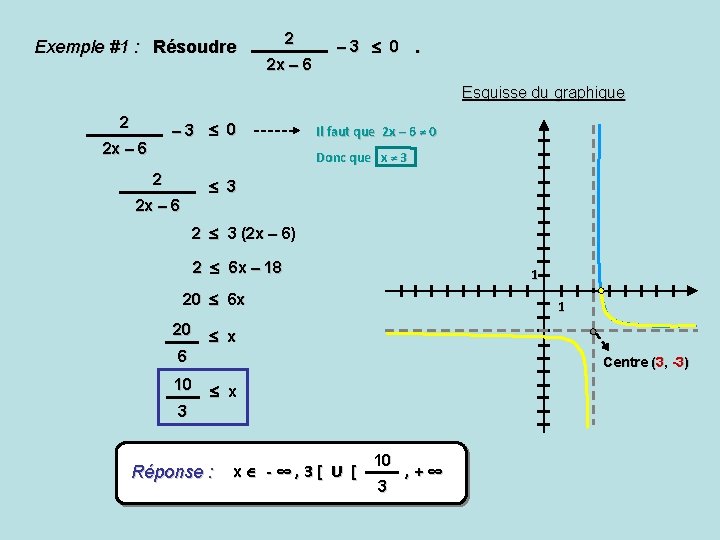
Exemple #1 : Résoudre 2 2 x – 6 – 3 0 . Esquisse du graphique 2 – 3 0 2 x – 6 Il faut que 2 x – 6 ≠ 0 Donc que x ≠ 3 2 x – 6 2 3 (2 x – 6) 2 6 x – 18 1 20 6 x 20 1 x 6 10 Centre (3, -3) x 3 Réponse : x -∞, 3[ U [ 10 3 , +∞

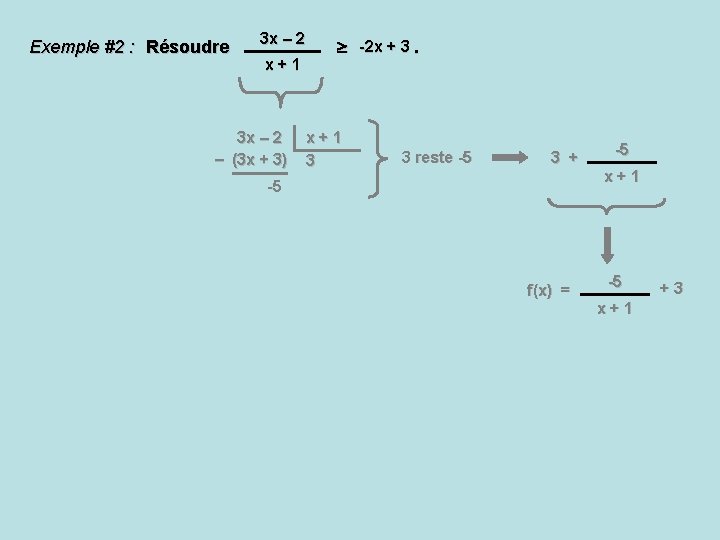
Exemple #2 : Résoudre 3 x – 2 x+1 3 x – 2 – (3 x + 3) -2 x + 3. x+1 3 3 reste -5 3 + -5 f(x) = -5 x+1 +3

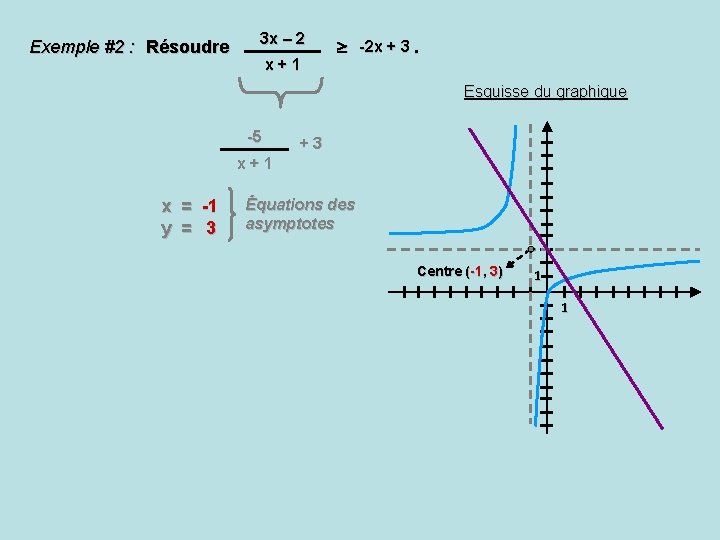
Exemple #2 : Résoudre 3 x – 2 x+1 -2 x + 3. Esquisse du graphique -5 +3 x+1 x = -1 y = 3 Équations des asymptotes Centre (-1, 3) 1 1

3 x – 2 Exemple #2 : Résoudre x+1 -2 x + 3. Esquisse du graphique 3 x – 2 -2 x + 3 Il faut que x + 1 ≠ 0 x+1 Donc que x ≠ -1 3 x – 2 (x + 1) (-2 x + 3) 3 x – 2 -2 x 2 + 3 x – 2 x + 3 0 -2 x 2 – 2 x + 5 x = -b b 2 – 4 ac -(-2) 1 1 2 a x = Centre (-1, 3) (-2)2 – 4(-2)(5) 2(-2) x = 2 44 -4 x 1 ≈ -2, 16 et x 2 ≈ 1, 16 Réponse : x [ -2, 16 , -1 [ U [ 1, 16 , + ∞