LES FONCTIONS DERIVEES Coefficient directeur dune droite Sens








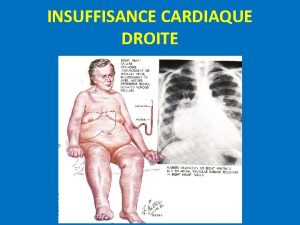
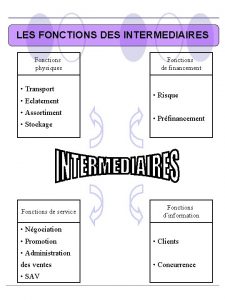
- Slides: 21

LES FONCTIONS DERIVEES Coefficient directeur d’une droite Sens de variation Tangente à une courbe Investigation Fonction dérivée Nombre dérivé Fonction dérivée et sens de variation Formules Séquence détente

Coefficient directeur d’une droite y a) Tracez la droite (AB) passant par les points A(2; 1) et B(4; 3) c -3 2 D +2 B 2 A 1 x 0 1 E b) Déterminez le coefficient directeur de la droite (AB) d) Déterminez le coefficient directeur de la droite (CD) F e) Déterminez le coefficient directeur de la droite (EF) a=0

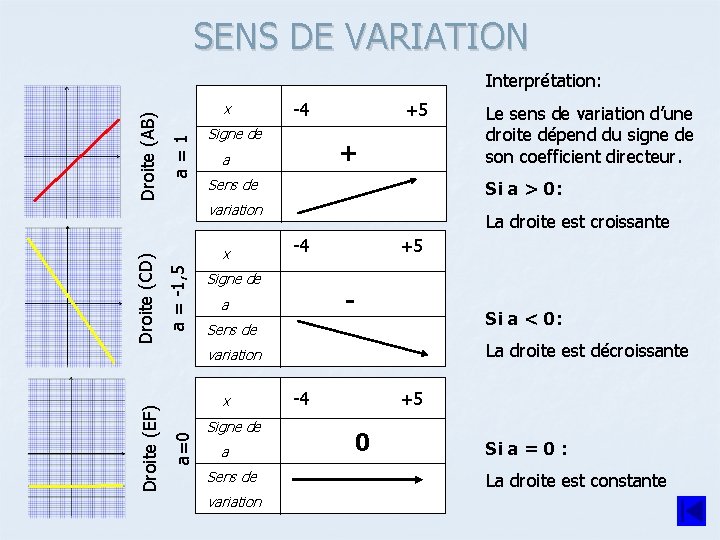
SENS DE VARIATION a=1 x -4 Signe de +5 + a Sens de x La droite est croissante -4 Signe de +5 - a Si a < 0: Sens de La droite est décroissante a=0 Droite (EF) variation x Signe de a Sens de variation Le sens de variation d’une droite dépend du signe de son coefficient directeur. Si a > 0: variation a = -1, 5 Droite (CD) Droite (AB) Interprétation: -4 +5 0 Si a = 0 : La droite est constante

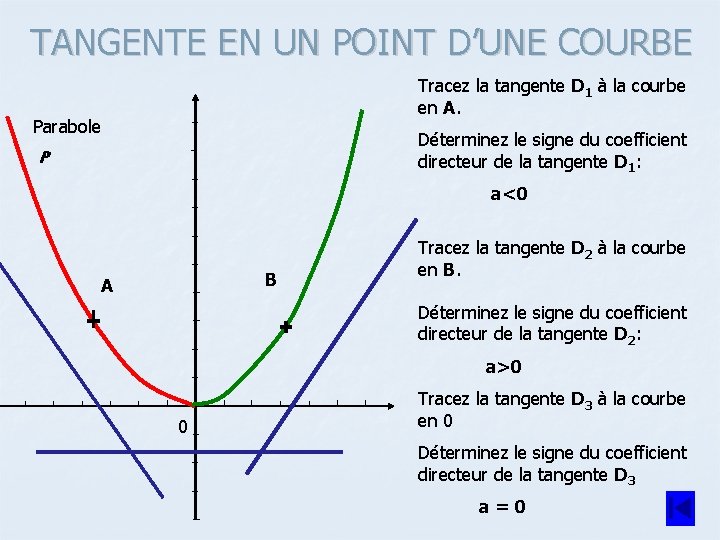
TANGENTE EN UN POINT D’UNE COURBE Tracez la tangente D 1 à la courbe en A. Parabole Déterminez le signe du coefficient directeur de la tangente D 1: P a<0 B A Tracez la tangente D 2 à la courbe en B. Déterminez le signe du coefficient directeur de la tangente D 2: a>0 0 Tracez la tangente D 3 à la courbe en 0 Déterminez le signe du coefficient directeur de la tangente D 3 a=0

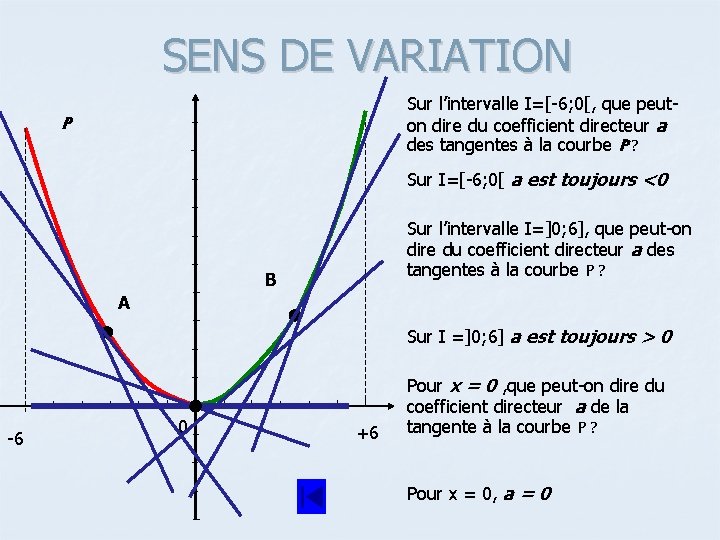
SENS DE VARIATION Sur l’intervalle I=[-6; 0[, que peuton dire du coefficient directeur a des tangentes à la courbe P ? P Sur I=[-6; 0[ a est toujours <0 Sur l’intervalle I=]0; 6], que peut-on dire du coefficient directeur a des tangentes à la courbe P ? B A Sur I =]0; 6] a est toujours > 0 -6 0 +6 Pour x = 0 , que peut-on dire du coefficient directeur a de la tangente à la courbe P ? Pour x = 0, a = 0

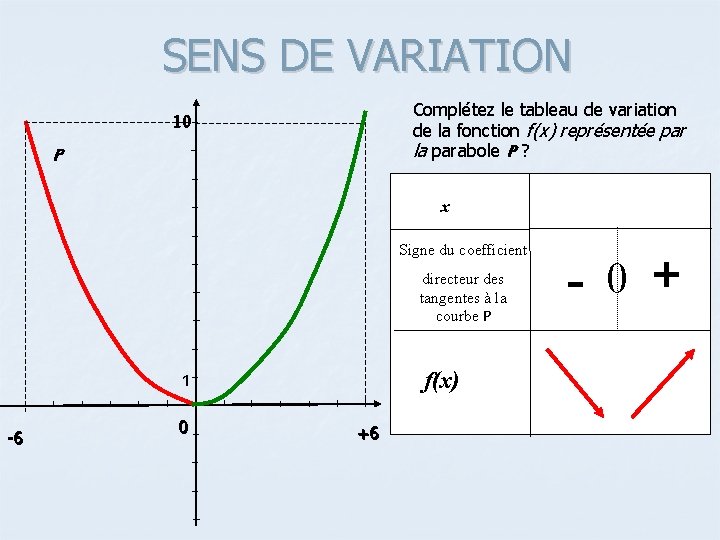
SENS DE VARIATION Complétez le tableau de variation de la fonction f(x) représentée par la parabole P ? 10 P x Signe du coefficient directeur des tangentes à la courbe P f(x) 1 -6 0 +6 - 0 +

INVESTIGATION ( Complétez) F(x) x -4 - 0 Signe de a +5 -4 f(x) 0 1 + 0 4 6 -3 -2 x 5 -4 -1 -2 -4 5 f(x) x Signe de a f(x) -1 + Signe de a 1 -2 -4 1) On savait déjà faire! 5 0 On donne la courbe représentative d’une fonction f, puis on en déduit le tableau de variation +5 2) On sait faire maintenant! - On connaît le tableau de variation, on en déduit la courbe représentative de la fonction f. 5 1 5 3) On ne sait pas encore faire! On donne une fonction, par exempe f(x) = x 2 , et on veut tracer sa courbe représentative

INVESTIGATION Il est en effet plus facile de tracer une courbe à partir d’un tableau de variation qui détermine sur quel intervalle la fonction est décroissante, constante ou croissante. Mais comment déterminer le signe du coefficient directeur sur un intervalle donné? ? ? Un peu d’aide !!!

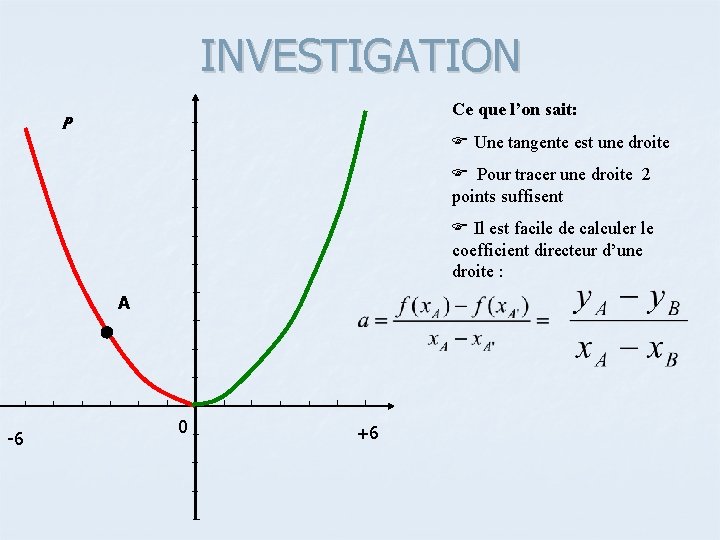
INVESTIGATION Ce que l’on sait: P Une tangente est une droite Pour tracer une droite 2 points suffisent Il est facile de calculer le coefficient directeur d’une droite : A -6 0 +6

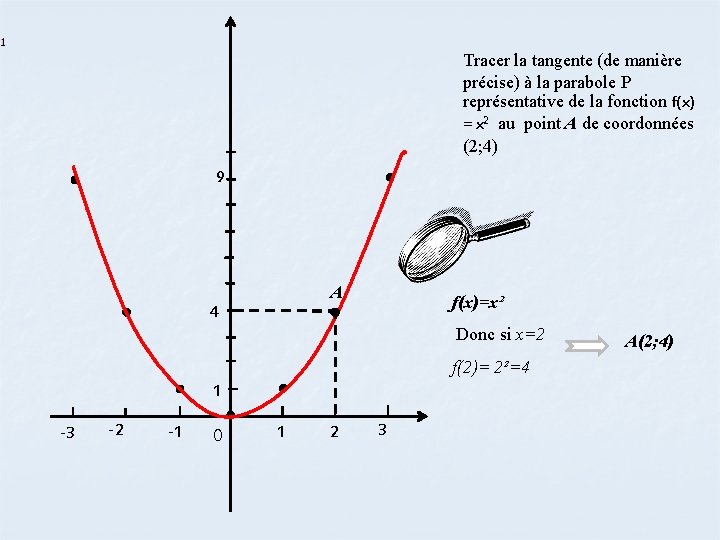
Tracer la tangente (de manière précise) à la parabole P représentative de la fonction f(x) = x 2 au point A de coordonnées (2; 4) 9 A f(x)=x² 4 Donc si x=2 f(2)= 2²=4 1 -3 -2 -1 1 2 3 A(2; 4)

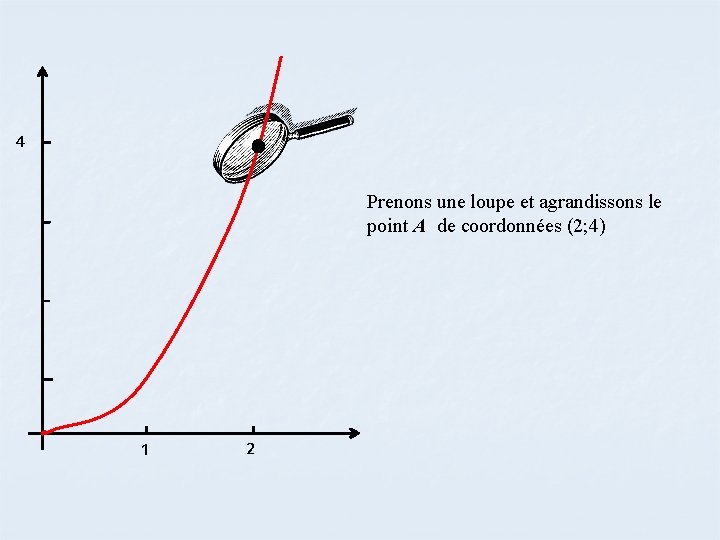
4 Prenons une loupe et agrandissons le point A de coordonnées (2; 4) 1 2

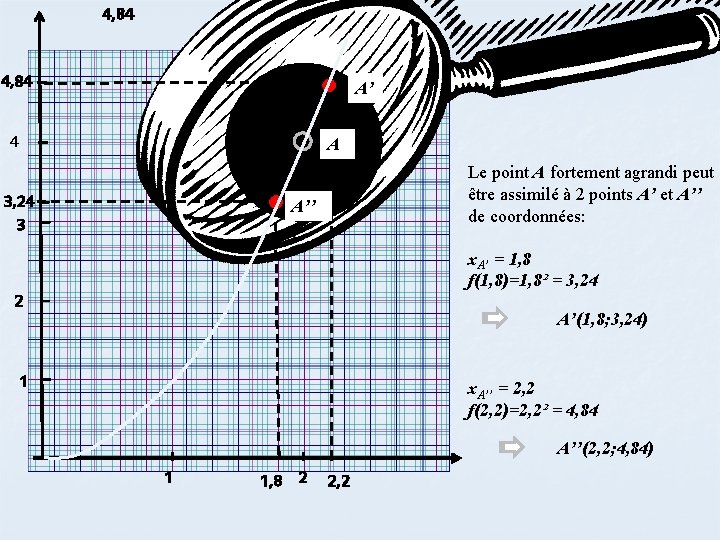
4, 84 A’ 4 A 3, 24 3 Le point A fortement agrandi peut être assimilé à 2 points A’ et A’’ de coordonnées: A’’ x. A’ = 1, 8 f(1, 8)=1, 8² = 3, 24 2 A’(1, 8; 3, 24) 1 x. A’’ = 2, 2 f(2, 2)=2, 2² = 4, 84 A’’(2, 2; 4, 84) 1 1, 8 2 2, 2

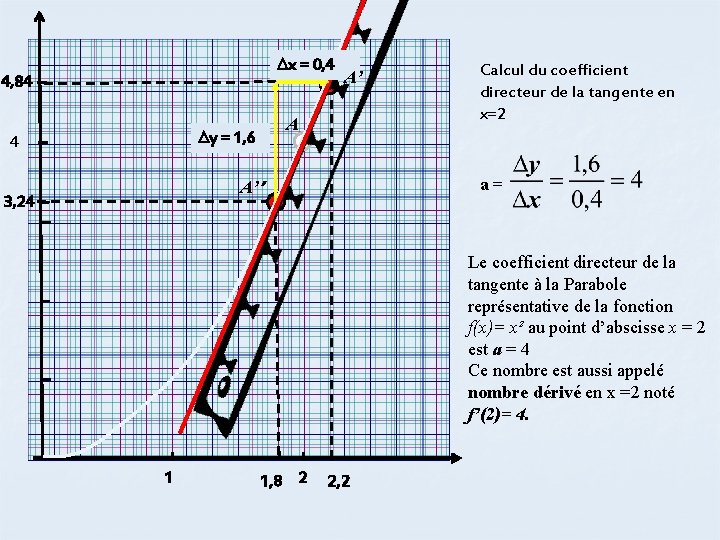
x = 0, 4 4, 84 A y = 1, 6 4 A’ a= A’’ 3, 24 Calcul du coefficient directeur de la tangente en x=2 Le coefficient directeur de la tangente à la Parabole représentative de la fonction f(x)= x² au point d’abscisse x = 2 est a = 4 Ce nombre est aussi appelé nombre dérivé en x =2 noté f’(2)= 4. 1 1, 8 2 2, 2

La fonction qui permet de trouver en tout point de la courbe le coefficient directeur de la tangente (donc le nombre dérivé) est appelée fonction dérivée notée f’ De la même manière que précédemment , trouvez la fonction dérivée f’ de la fonction f(x) = x²

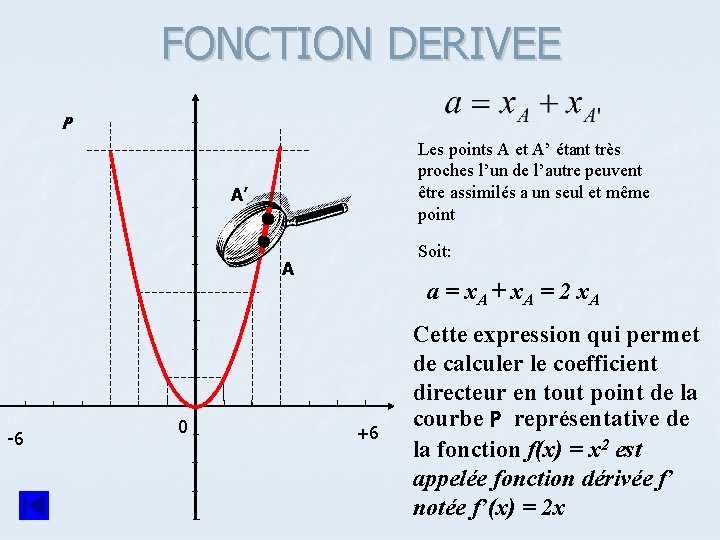
FONCTION DERIVEE: Prenons 2 points quelconques A et A’ très proches l’un de l’autre de la parabole P représentative de la fonction f(x) = x 2 tel que A(x; y) et A’(x’; y’). P A’ A A -6 0 Calculez le coefficient directeur de la tangente en A qui après agrandissement peut être comparé aux 2 points A et A’ +6

FONCTION DERIVEE P Les points A et A’ étant très proches l’un de l’autre peuvent être assimilés a un seul et même point A’ Soit: A -6 0 a = x. A + x. A = 2 x. A +6 Cette expression qui permet de calculer le coefficient directeur en tout point de la courbe P représentative de la fonction f(x) = x 2 est appelée fonction dérivée f’ notée f’(x) = 2 x

NOMBRE DERIVEE On vient de définir la fonction dérivée de f: on la note f’ P f’(x) = 2 x Calculez le coefficient directeur de la tangente à la courbe P au point A d’abscisse x=3 a = f’(3)= 2 3 = 6 A Ce nombre est aussi appelé nombre dérivé -6 Calculez le nombre dérivé, f’(-2) puis tracez la tangente à la courbe P au point A d’abscisse x=-2 -4 -1 -6 - 3 -2 1 0 A f’(-2) = 2 -2 = -4 +3 +6 Vérifiez que la tangente à P en x = 0 est constante. f’(x) = 2 0 = 0

FONCTION DERIVEE ET SENS DE VARIATION Comment exploiter la fonction dérivée f’ pour connaître le sens de variation de la fonction f sur I=[-3; +3] ? ? ? f(x)= x 2 alors f’(x) = 2 x P 9 Le sens de variation dépend du signe de f’(x). ETUDE DU SIGNE DE f’ Cf’(x) = O soit 2 x = 0 pour x = 0 4 Cf’(x) < 0 soit 2 x < 0 pour x < 0 f’(x) > 0 soit 2 x > 0 pour x > 0 Tableau de variation -3 0 x Signe de f’(x) f(x) - 0 + +3 1 f(-3)= 9 f(0)= 0 f(3)= 9 -3 0 3

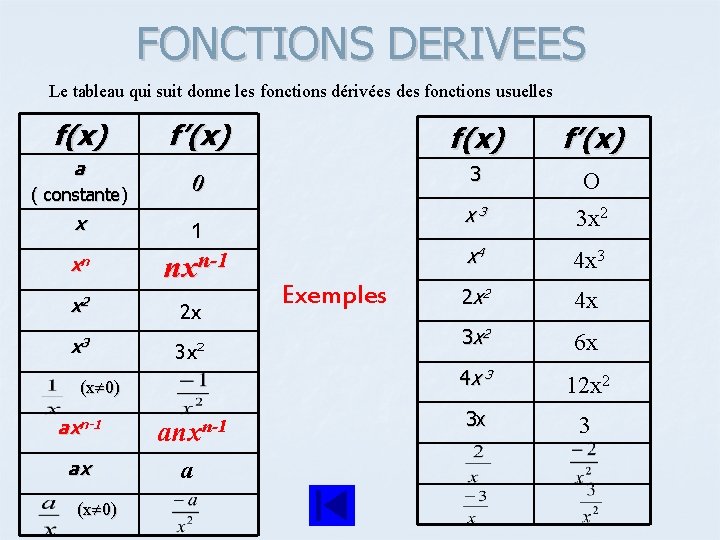
FONCTIONS DERIVEES Le tableau qui suit donne les fonctions dérivées des fonctions usuelles f(x) a ( constante) f’(x) 0 3 O x 3 3 x 2 x 4 4 x 3 2 x 2 4 x 3 x 2 6 x 4 x 3 12 x 2 3 x 3 x 1 xn nxn-1 x 2 x 3 2 x 3 x² (x 0) axn-1 anxn-1 ax a (x 0) Exemples

SEQUENCE DETENTE Comment appelle-t-on ces deux parties de l’espace parfaitement identique ? ? ? Un canard parce que coin-coin

 Coefficient directeur d'une droite
Coefficient directeur d'une droite Sens propre sens figuré exercices corrigés cm1
Sens propre sens figuré exercices corrigés cm1 Fonctions et solutions techniques
Fonctions et solutions techniques Coefficient directeur
Coefficient directeur Les fonctions mécaniques élémentaires
Les fonctions mécaniques élémentaires Liaison complète ou partielle
Liaison complète ou partielle Les 6 fonctions du langage
Les 6 fonctions du langage Les fonctions de la famille
Les fonctions de la famille Dialogue cinéma
Dialogue cinéma Les fonctions dans le groupe verbal
Les fonctions dans le groupe verbal Les 5 fonctions de la peau
Les 5 fonctions de la peau Dérivée fonction composée
Dérivée fonction composée Les cinq sens prononciation
Les cinq sens prononciation Picto directeur
Picto directeur Noyau aromatique
Noyau aromatique Plan directeur sectoriel
Plan directeur sectoriel Olivier milleron
Olivier milleron évaluation ce1
évaluation ce1 Titres et fonctions
Titres et fonctions Fonctions exécutives
Fonctions exécutives Fonctions des engrenages
Fonctions des engrenages Engrenage droit à denture droite
Engrenage droit à denture droite