FONCTIONS cours 14 Les fonctions gros les fonctions













- Slides: 30

FONCTIONS cours 14

Les fonctions gros, les fonctions servent à expliciter un lien entre deux quantité Vous devriez déjà avoir une connaissance des fonctions, donc ce qui suit est une petite révision. Ou du moins, des notions connues vues sous un nouvel angle.

Définition: Une relation entre deux ensembles et un sous-ensemble du produit cartésien. Exemple: Est une relation car est

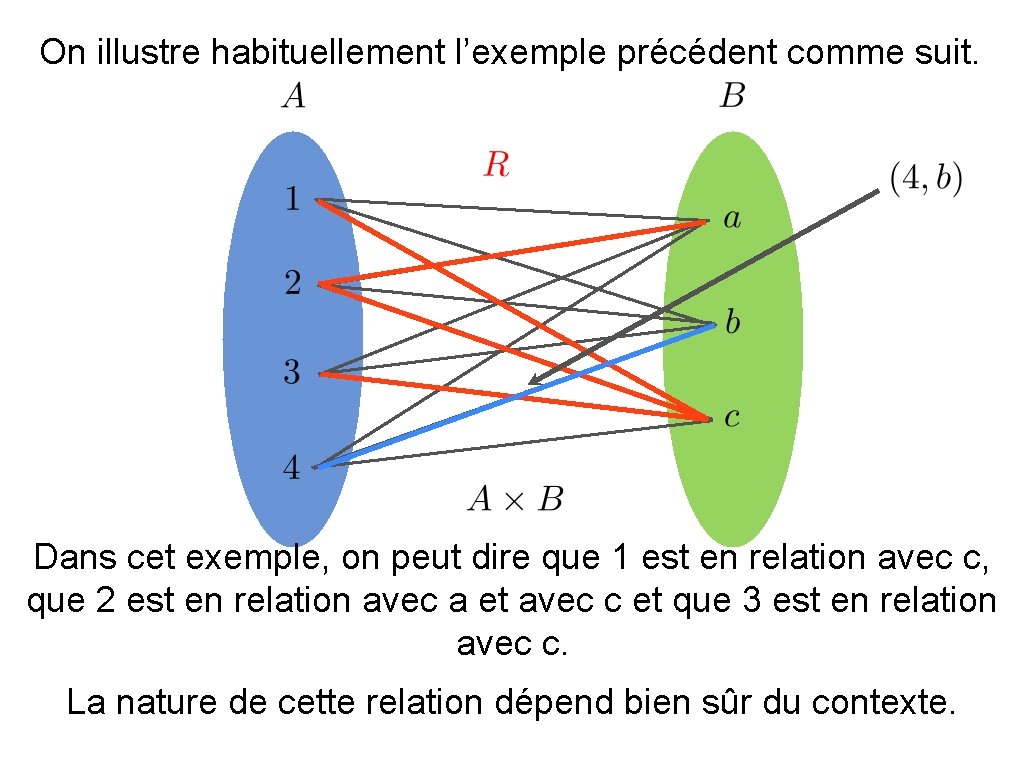
On illustre habituellement l’exemple précédent comme suit. Dans cet exemple, on peut dire que 1 est en relation avec c, que 2 est en relation avec a et avec c et que 3 est en relation avec c. La nature de cette relation dépend bien sûr du contexte.

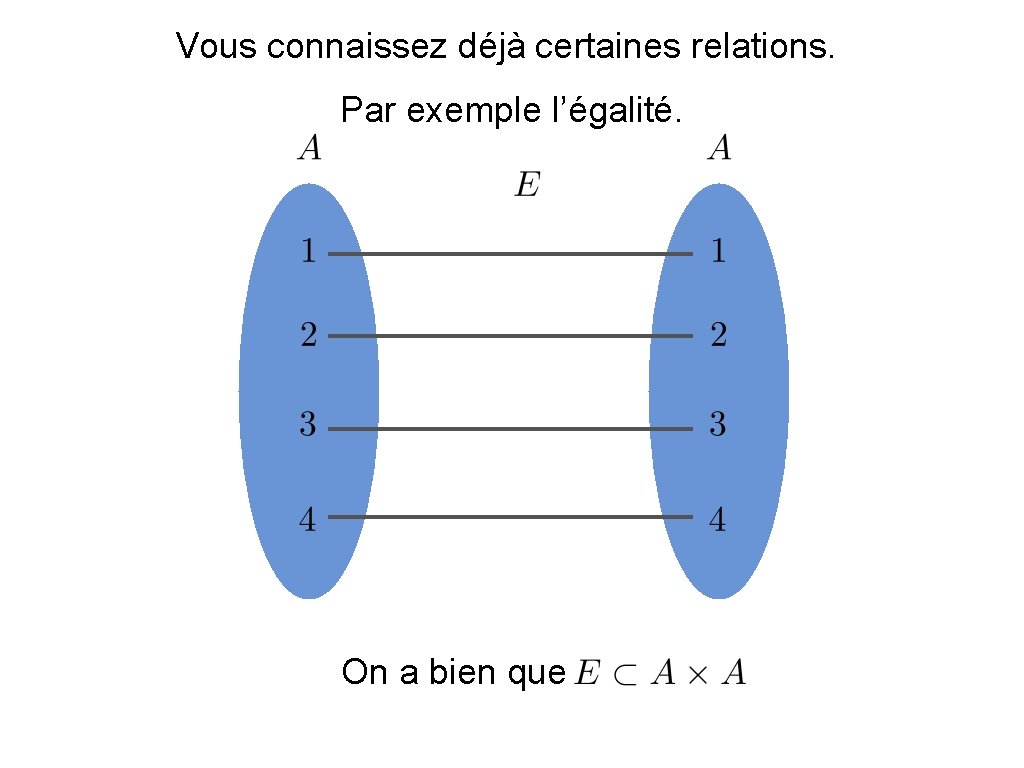
Vous connaissez déjà certaines relations. Par exemple l’égalité. On a bien que

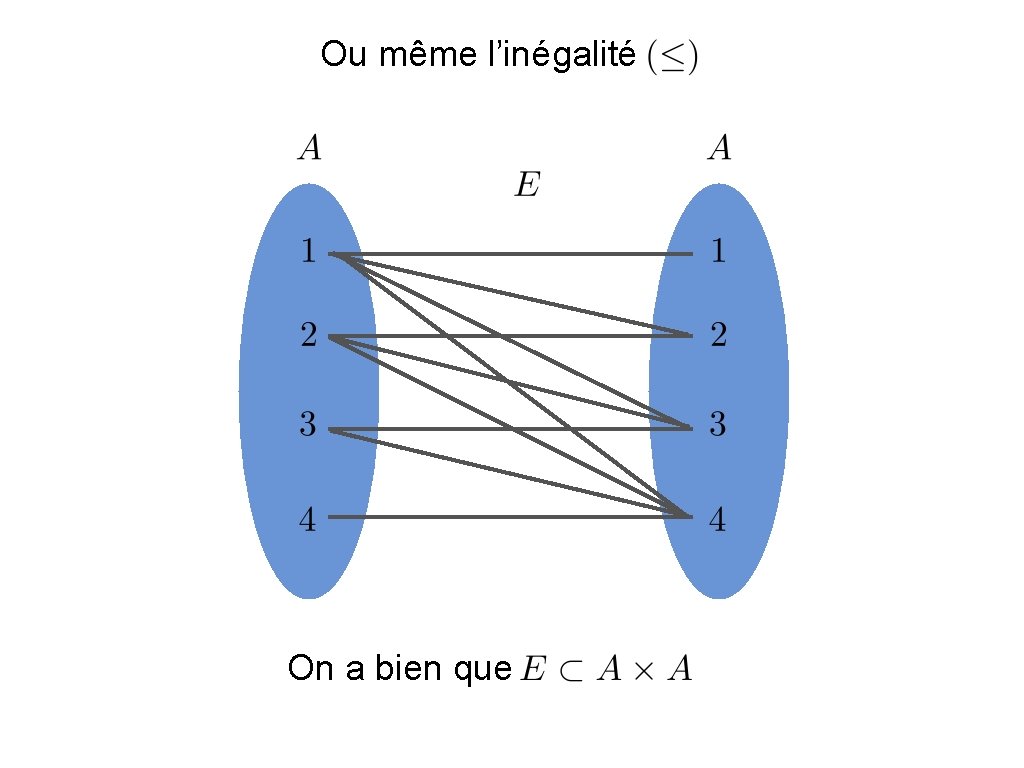
Ou même l’inégalité On a bien que

La raison qu’on vient de parler de relation est qu’une fonction est un cas particulier de relation. Définition: Une fonction est une relation telle que chaque élément d’un des deux ensembles (qu’on nomme l’ensemble de départ) est en relation avec au plus un élément de l’autre ensemble (qu’on nomme l’ensemble d’arrivé).

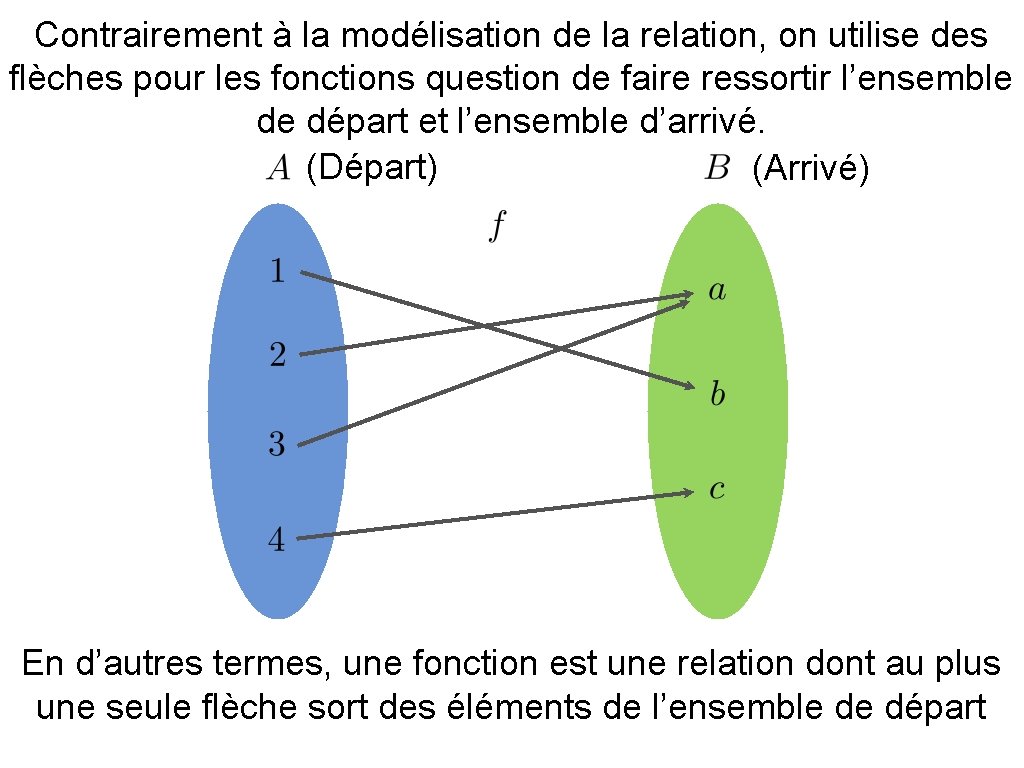
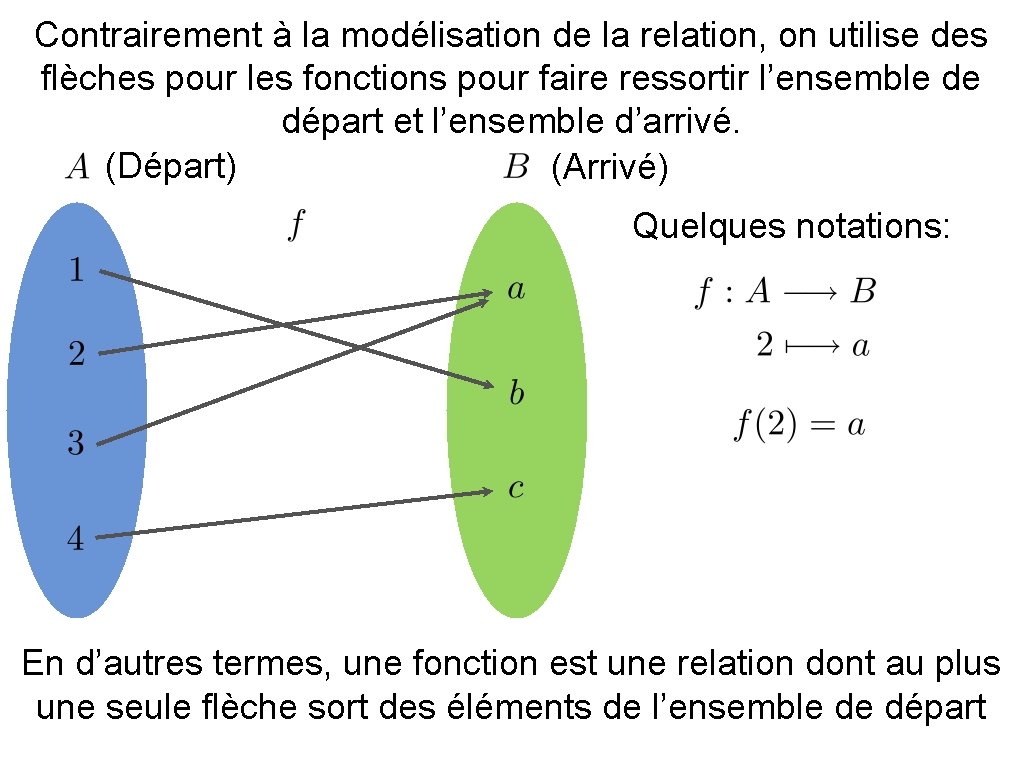
Contrairement à la modélisation de la relation, on utilise des flèches pour les fonctions question de faire ressortir l’ensemble de départ et l’ensemble d’arrivé. (Départ) (Arrivé) En d’autres termes, une fonction est une relation dont au plus une seule flèche sort des éléments de l’ensemble de départ

Contrairement à la modélisation de la relation, on utilise des flèches pour les fonctions pour faire ressortir l’ensemble de départ et l’ensemble d’arrivé. (Départ) (Arrivé) Quelques notations: En d’autres termes, une fonction est une relation dont au plus une seule flèche sort des éléments de l’ensemble de départ

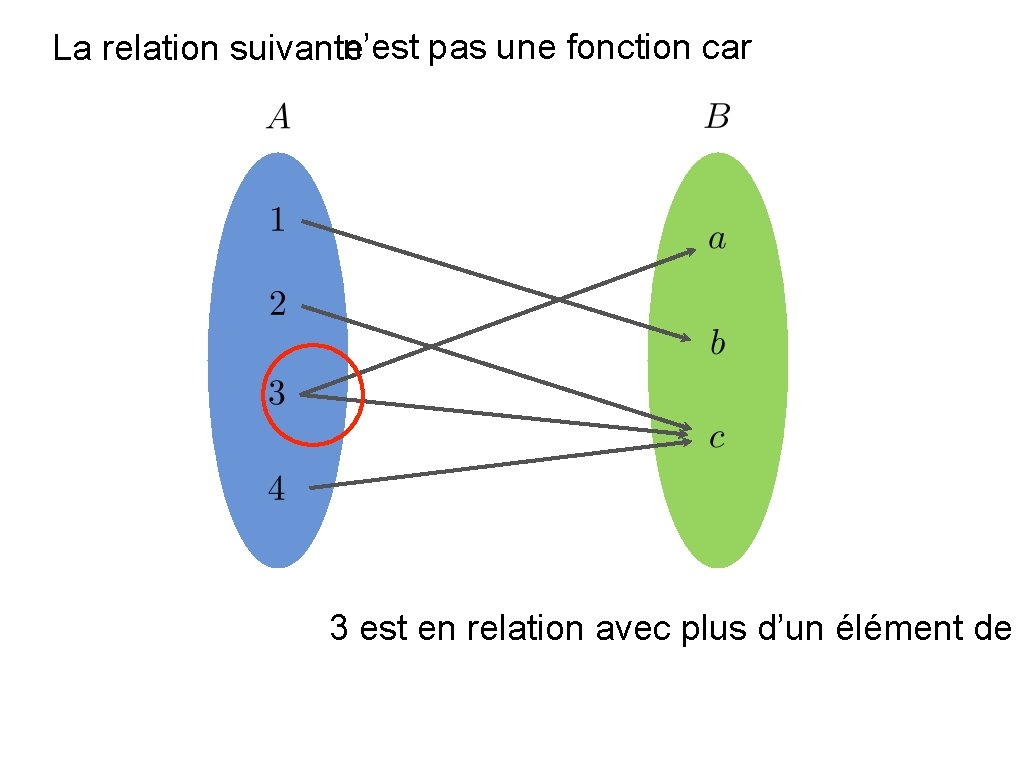
n’est pas une fonction car La relation suivante 3 est en relation avec plus d’un élément de B

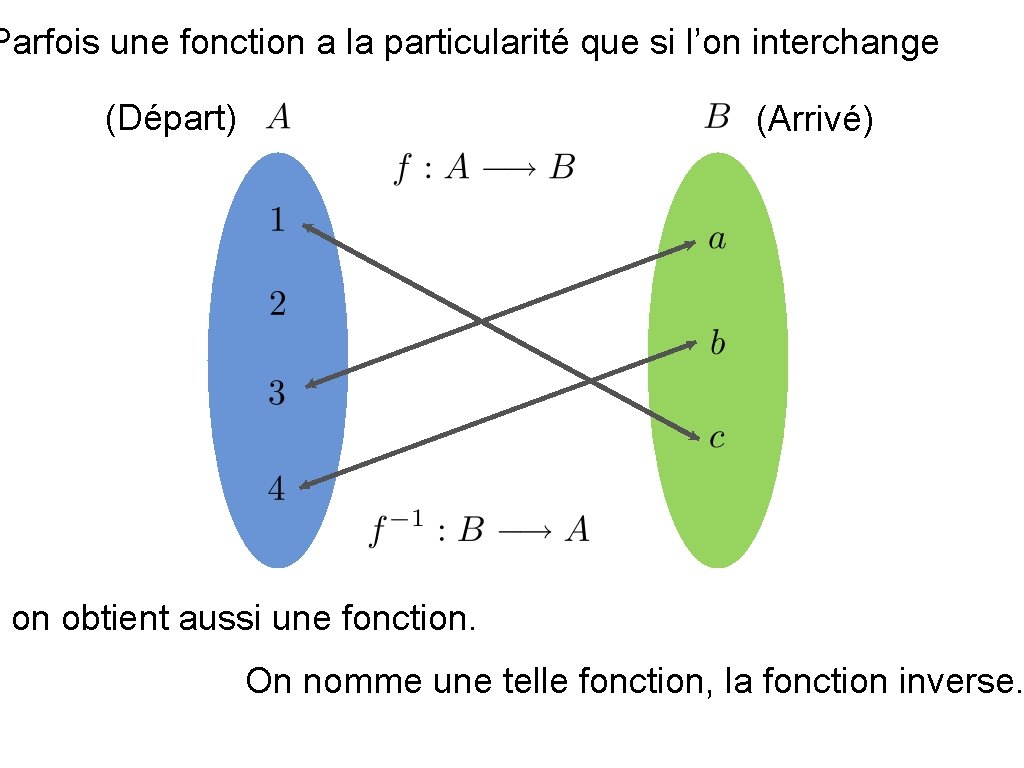
Parfois une fonction a la particularité que si l’on interchange (Départ) (Arrivé) on obtient aussi une fonction. On nomme une telle fonction, la fonction inverse.

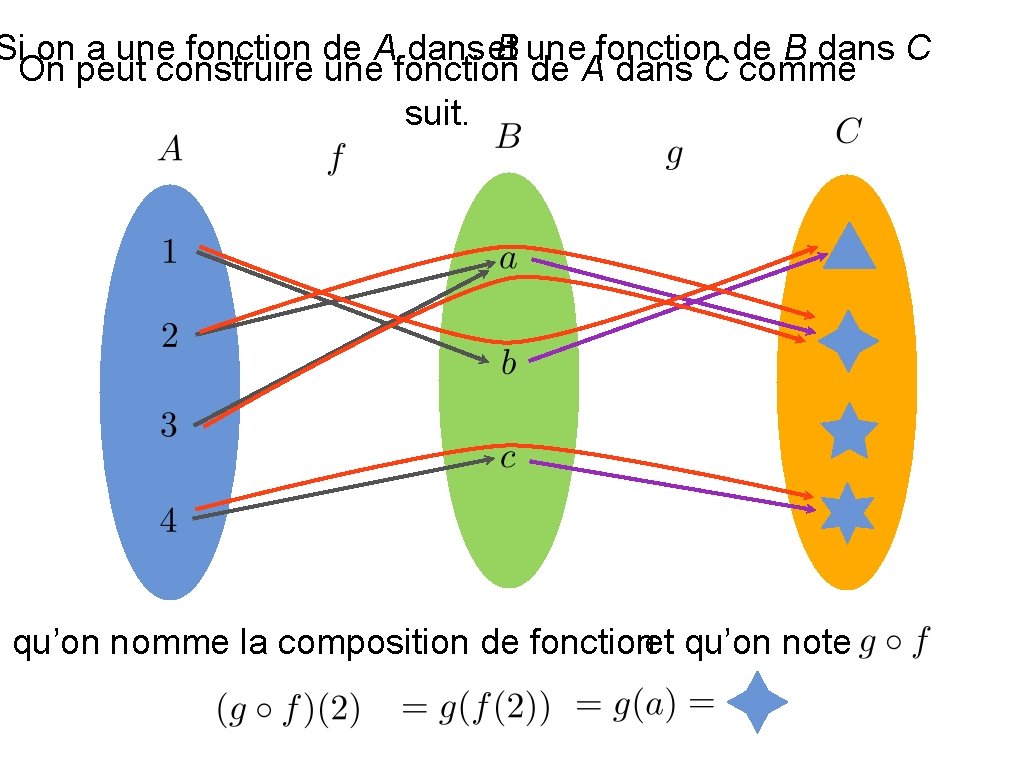
Si on a une fonction de A dans et B une fonction de B dans C On peut construire une fonction de A dans C comme suit. qu’on nomme la composition de fonctionet qu’on note

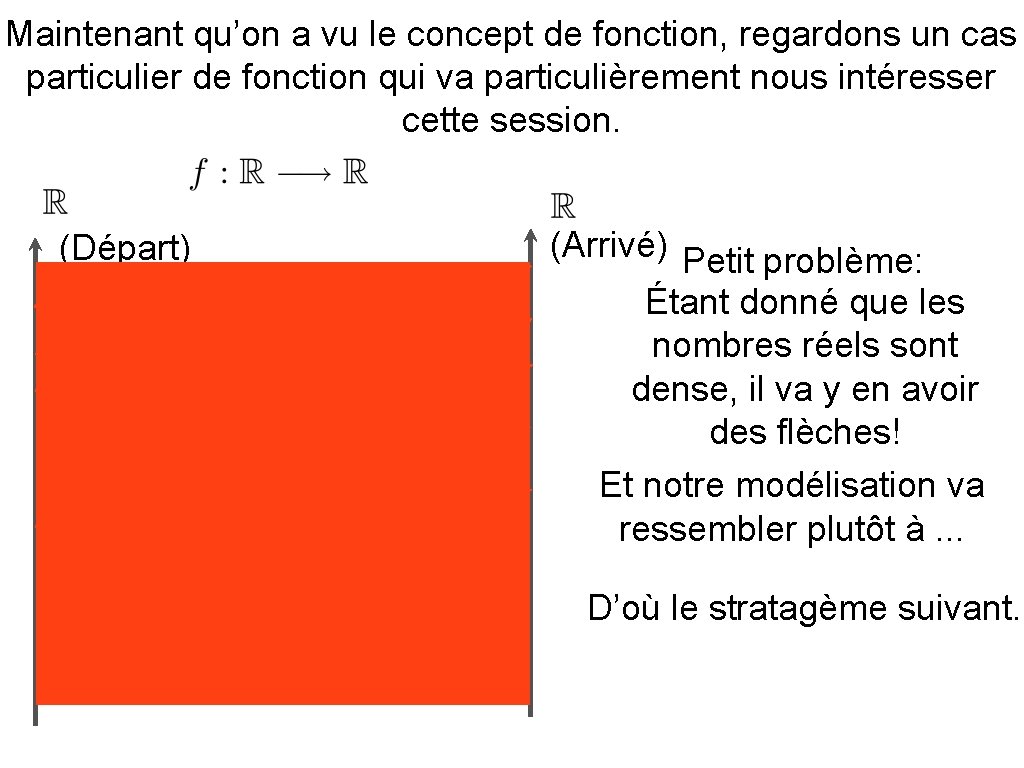
Maintenant qu’on a vu le concept de fonction, regardons un cas particulier de fonction qui va particulièrement nous intéresser cette session. (Départ) (Arrivé) Petit problème: Étant donné que les nombres réels sont dense, il va y en avoir des flèches! Et notre modélisation va ressembler plutôt à. . . D’où le stratagème suivant.

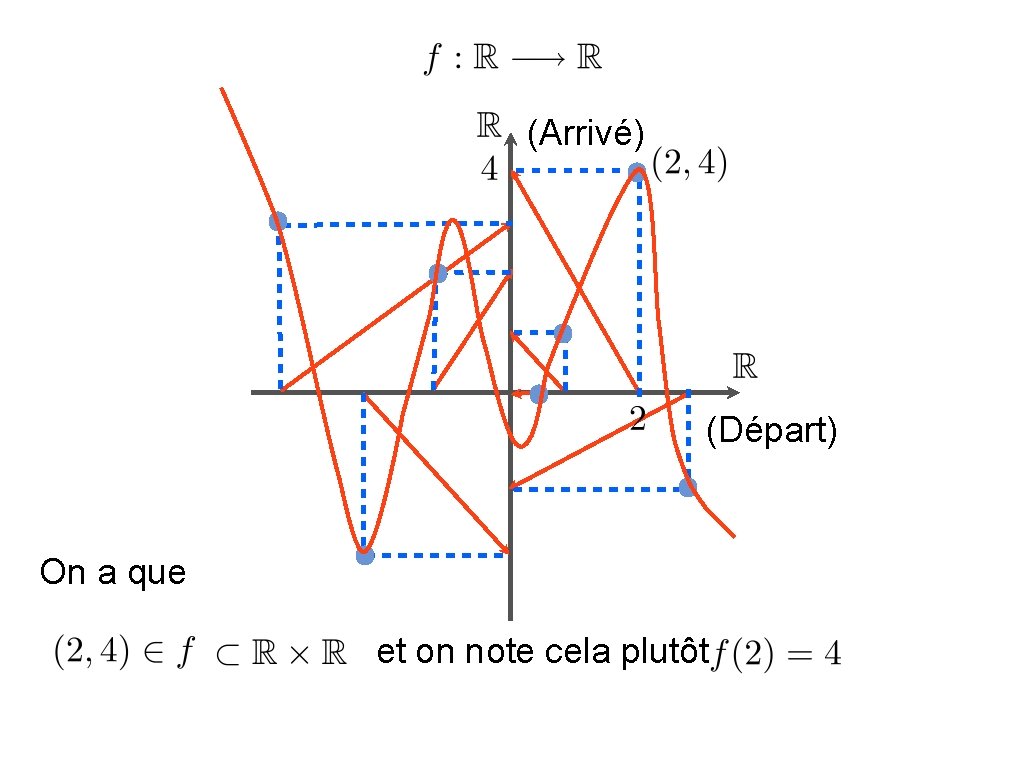
(Arrivé) (Départ) On a que et on note cela plutôt

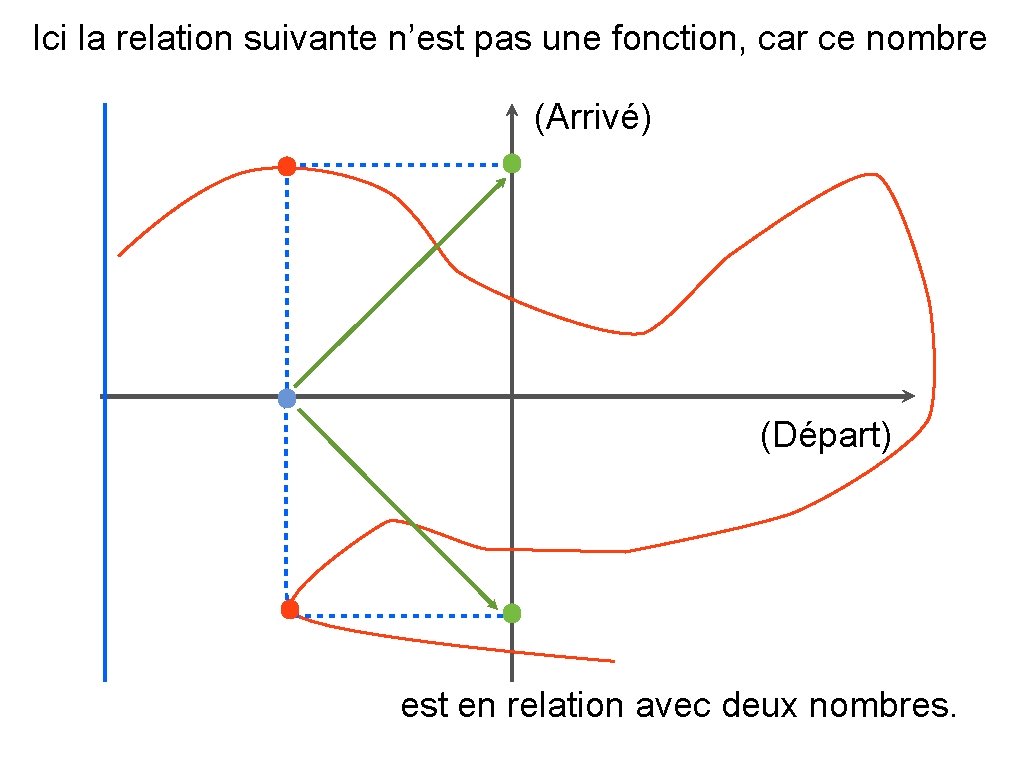
Ici la relation suivante n’est pas une fonction, car ce nombre (Arrivé) (Départ) est en relation avec deux nombres.

Faites les exercices suivants # 2. 19 et 2. 20

Bien qu’une fonction soit un ensemble de couples que chaque est en relation avec un unique telle on ne va pas les étudier sous cette forme aussi générale. On va plutôt étudier les fonctions qui sont données à l’aide d’une règle. Par exemple la fonction qu’on va noter plutôt comme suit

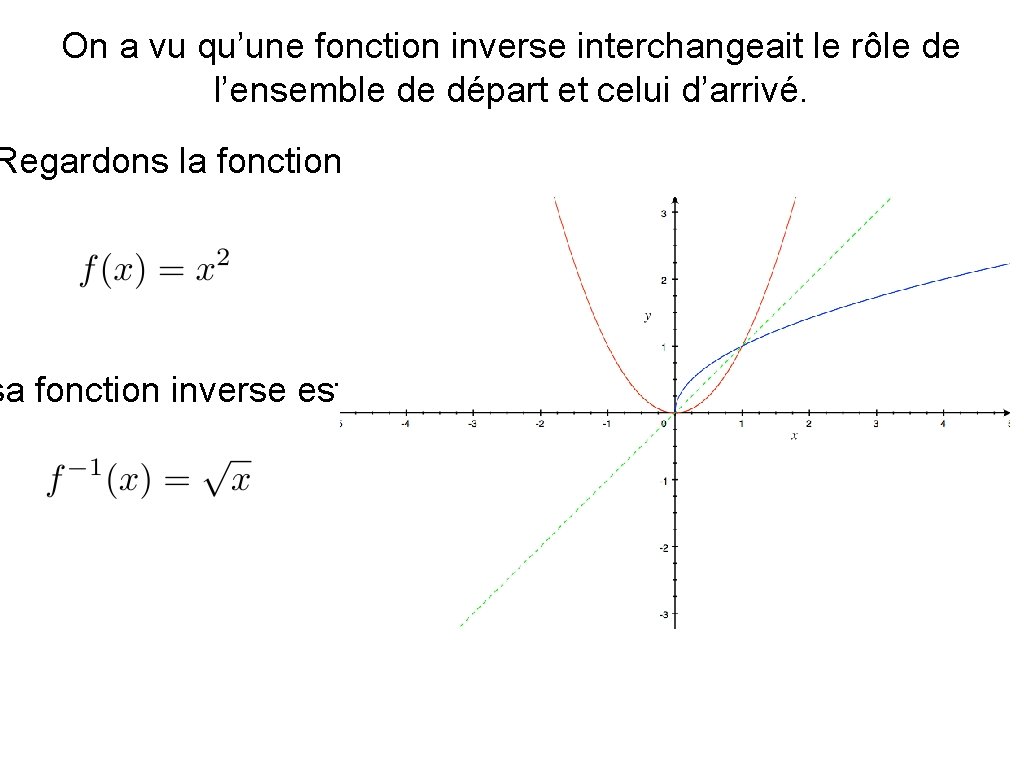
On a vu qu’une fonction inverse interchangeait le rôle de l’ensemble de départ et celui d’arrivé. Regardons la fonction sa fonction inverse est

Remarque: La composition de fonction n’est pas commutative. C’est à dire: Regardons ceci avec un exemple.

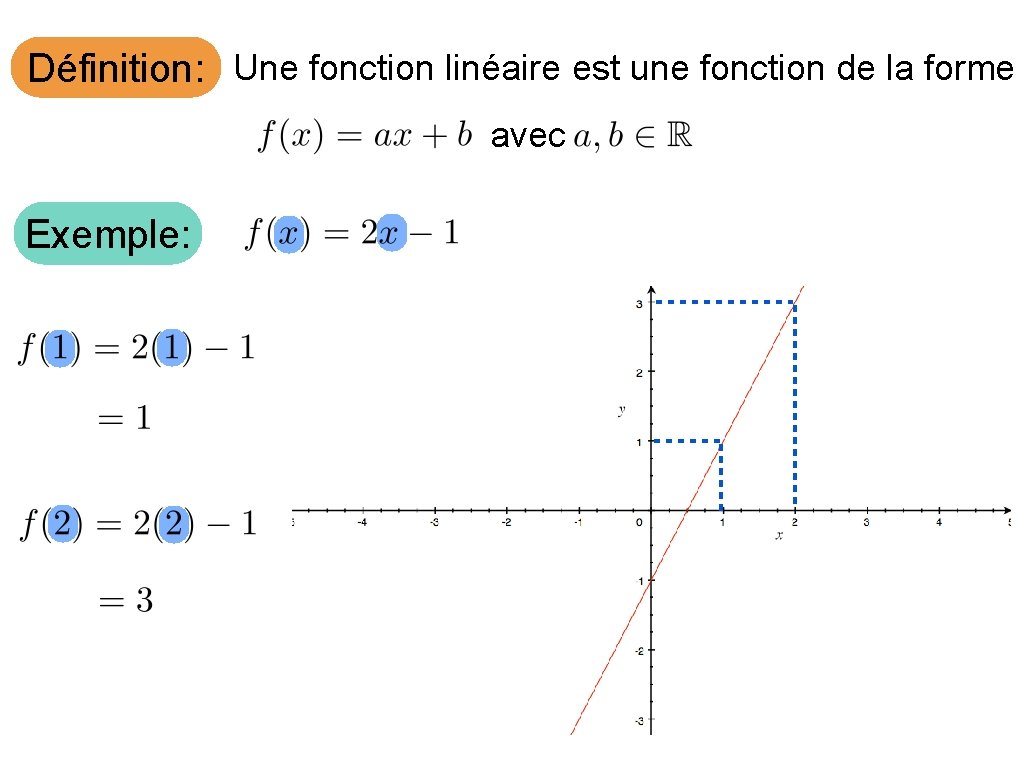
Définition: Une fonction linéaire est une fonction de la forme avec Exemple:

On écrit souvent les fonctions linéaires avec les lettres m et b. La pente L’ordonnée à l’origine ue b soit l’ordonnée à l’origine est assez direct. . . mais vous êtes vous déjà demandé pourquoi m est la pente?

Faites les exercices suivants #2. 21 à 2. 25

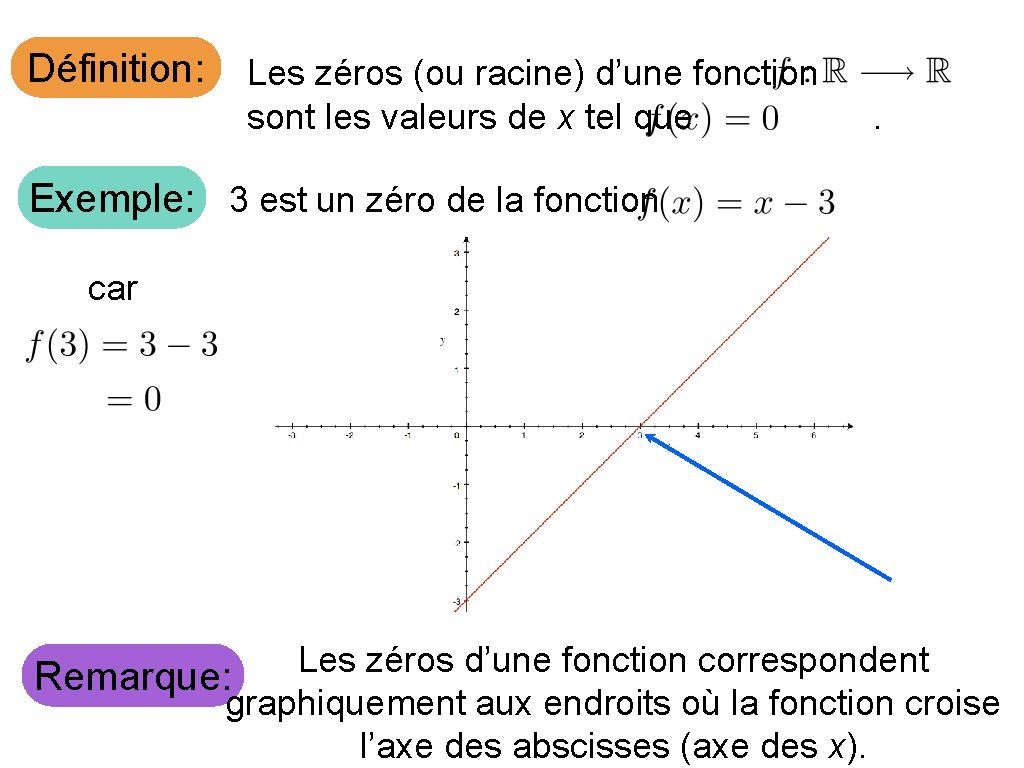
Définition: Les zéros (ou racine) d’une fonction sont les valeurs de x tel que . Exemple: 3 est un zéro de la fonction car Les zéros d’une fonction correspondent Remarque: graphiquement aux endroits où la fonction croise l’axe des abscisses (axe des x).

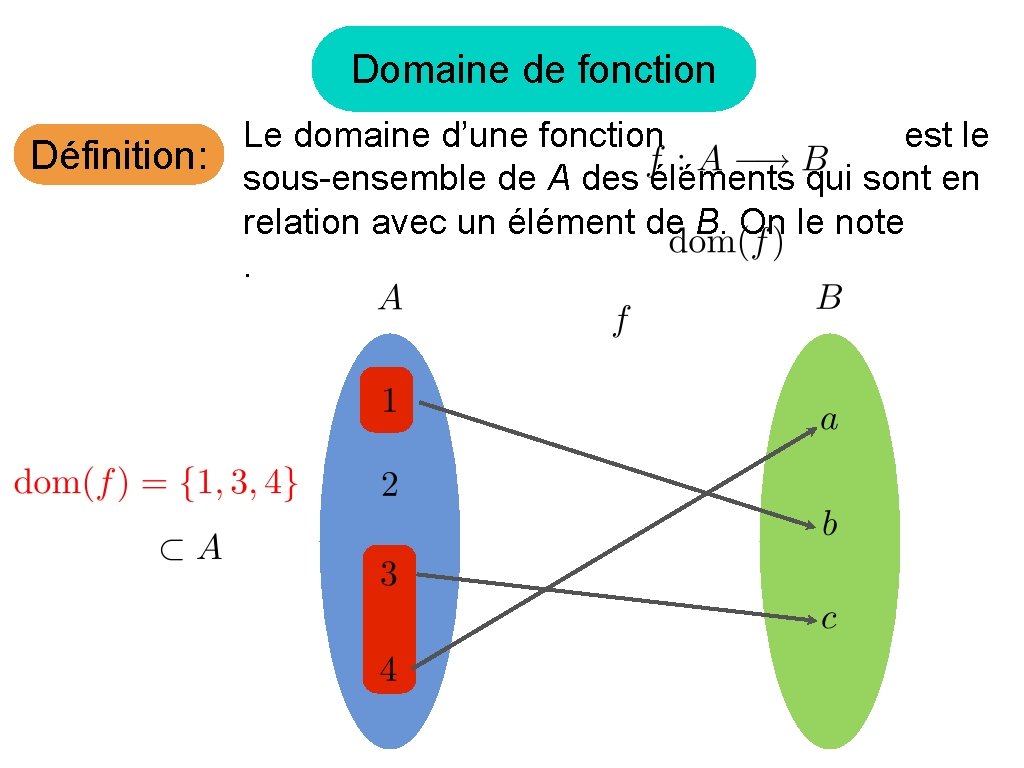
Domaine de fonction Le domaine d’une fonction est le Définition: sous-ensemble de A des éléments qui sont en relation avec un élément de B. On le note.

Lorsque la fonction est donnée à l’aide d’une expression algébrique, tous les x sont en relation avec l’expression évaluée en la valeur de x. Donc, il semblerait que le domaine de toute fonction soit tous !? ! En fait non! Car certaine expression non pas de sens pour certaine valeur de x Quels sont ces interdits en mathématiques?

n gros, il y trois choses qu’on ne peut pas faire en mathématique Diviser par zéro. Prendre une racine pair d’un nombre négatif. Prendre un logarithme d’un nombre négatif ou nul.

Exemple: Le domaine de la fonction est tous sauf les valeurs de x qui font en sorte qu Par la règle du produit nul, on a deux possibilités. et donc

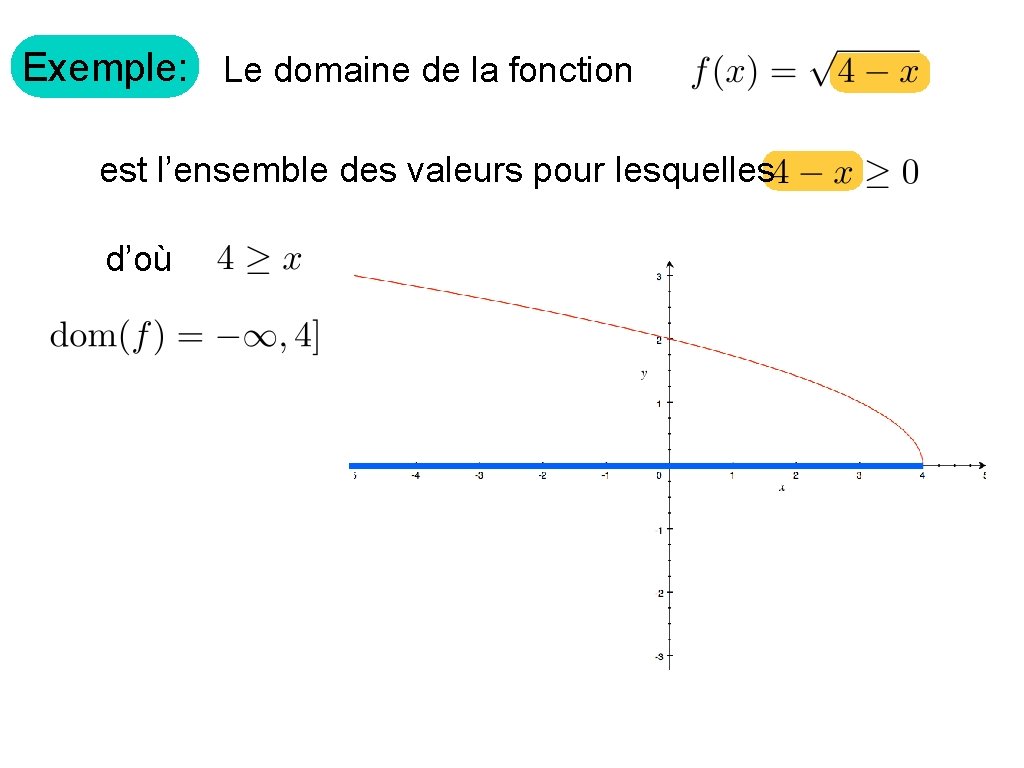
Exemple: Le domaine de la fonction est l’ensemble des valeurs pour lesquelles d’où

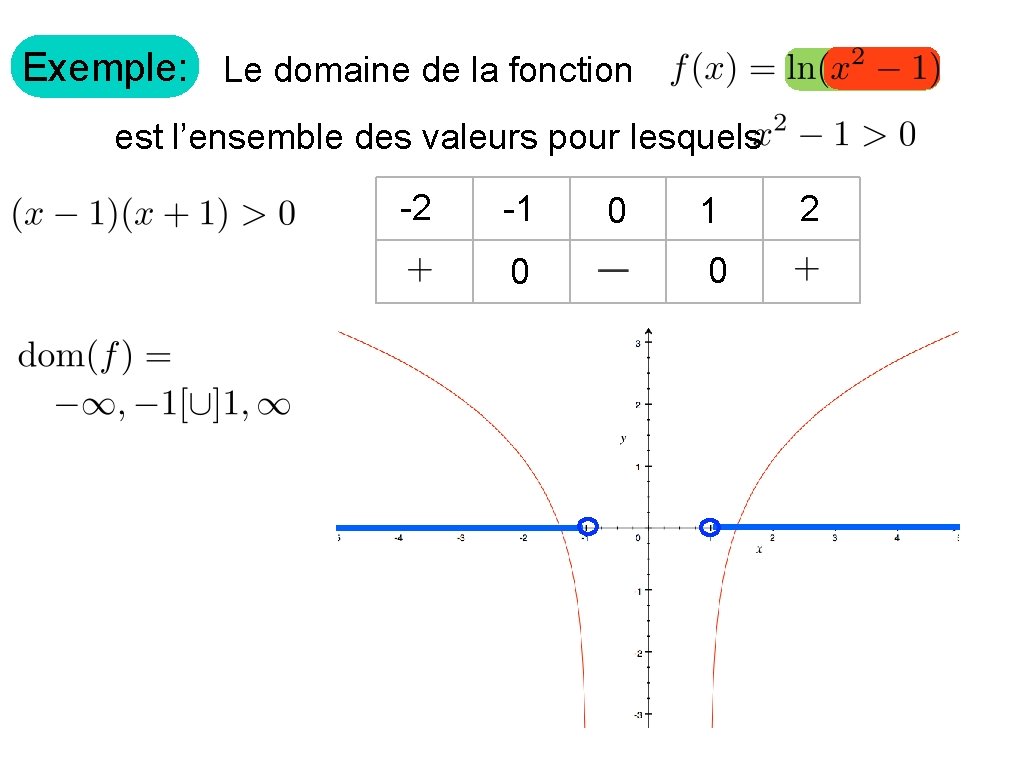
Exemple: Le domaine de la fonction est l’ensemble des valeurs pour lesquels -2 -1 0 0 1 0 2

Faites les exercices suivants #2. 26 et #2. 27
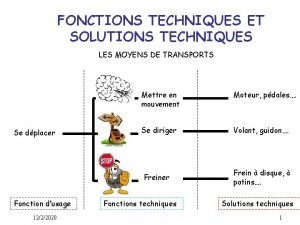
 Fonctions techniques et solutions techniques
Fonctions techniques et solutions techniques Groupe verbal
Groupe verbal Les 5 fonctions de la peau
Les 5 fonctions de la peau Les fonctions mécaniques élémentaires
Les fonctions mécaniques élémentaires Le rôle de la fonction technique
Le rôle de la fonction technique La fonction impressive
La fonction impressive Les fonctions de la famille
Les fonctions de la famille Raphaël chevènement
Raphaël chevènement Les anticoagulants cours ifsi
Les anticoagulants cours ifsi Les suites du cours
Les suites du cours Les incoterms cours
Les incoterms cours Cours sur la gestion axée sur les résultats
Cours sur la gestion axée sur les résultats Guillaume villemaud
Guillaume villemaud Hormone thyroïdienne
Hormone thyroïdienne Les helminthes cours
Les helminthes cours Compteur asynchrone modulo 5
Compteur asynchrone modulo 5 Cours sur les trames
Cours sur les trames J'aime les gros nichons
J'aime les gros nichons Hélène ségara on ne dit pas
Hélène ségara on ne dit pas Zoé et les gros monstres
Zoé et les gros monstres La plus grosse grue du monde
La plus grosse grue du monde Primitive
Primitive Fonctions des engrenages
Fonctions des engrenages Titres et fonctions
Titres et fonctions Fonctions exécutives
Fonctions exécutives Dérivée des fonctions usuelles
Dérivée des fonctions usuelles Cours mimo
Cours mimo Méthode hay grille
Méthode hay grille Cours ihm
Cours ihm Encadrement nombre chromatique
Encadrement nombre chromatique Drain thoracique surveillance infirmière
Drain thoracique surveillance infirmière