TRIGONOMETRI KOMPETENSI DASAR 3 15 Memahami konsep perbandingan

TRIGONOMETRI

KOMPETENSI DASAR 3. 15 Memahami konsep perbandingan trigonometri pada segitiga siku-siku melalui penyelidikan diskusi tentang hubungan perbandingan sisi-sisi yang bersesuaian dalam beberapa segitiga siku- siku sebangun

PENGERTIAN TRIGONOMETRI Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

TRIGONOMETRI • PERBANDINGAN TRIGONOMENTRI PADA SEGITIGA • RUMUS-RUMUS TRIGONOMETRI PADA SEGITIGA

NILAI TRIGONOMETRI SUDUT Perbandingan trigonometri pada segitiga siku-siku Secara umum, pada segitiga siku-siku yang sebangun, perbandingan sisi-sisi menurut salah satu sudutnya bernilai tetap. Perbandingan antara sepanjang sisi pada segitiga siku-siku yang sebangun itulah yang disebut perbandingan trigonometri. C Miring Depan α A Samping B

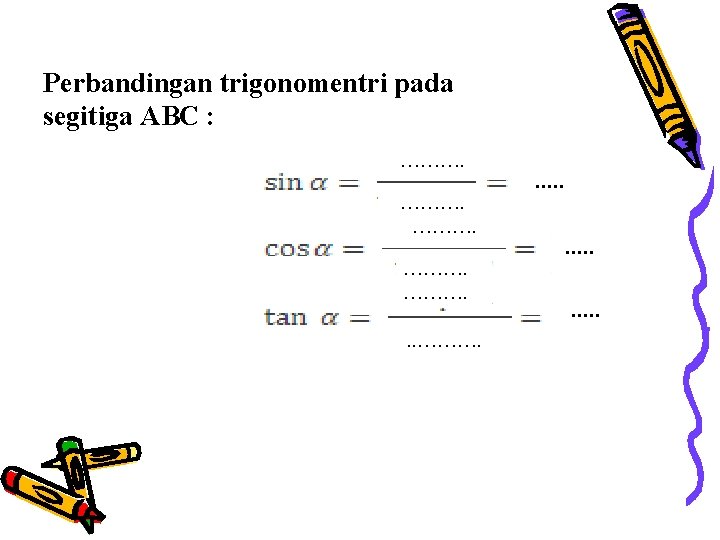
Perbandingan trigonomentri pada segitiga ABC : ………. . . . .

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA DALAM SUMBU KARTESIUS Sb y 1. Sinus = y r 2. Cosinus = 3. Tangan = x Sb x

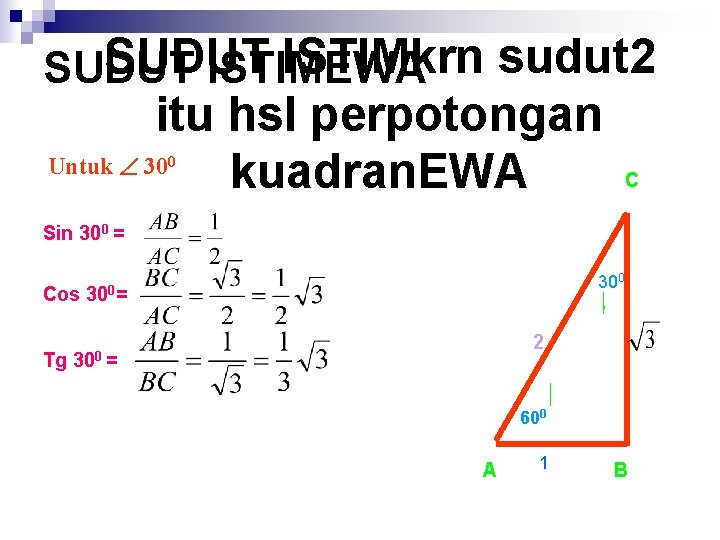
SUDUT ISTIMkrn sudut 2 SUDUT ISTIMEWA itu hsl perpotongan Untuk 30 kuadran. EWA 0 C Sin 300 = Cos Tg 300= 2 300 = 600 A 1 B

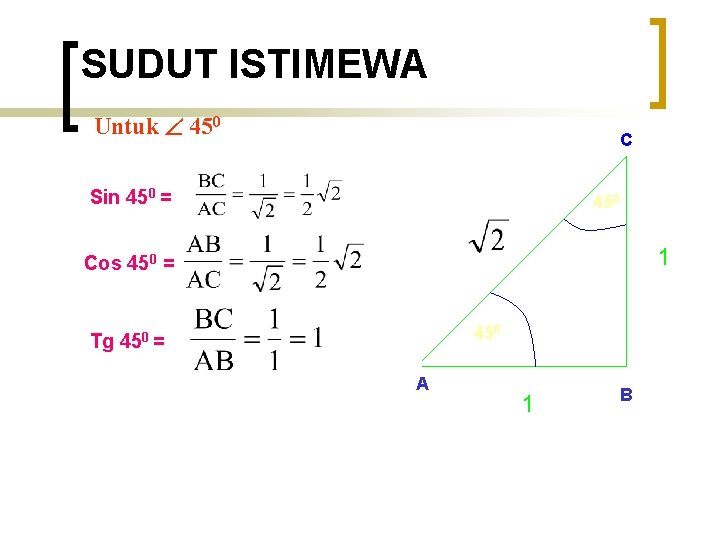
SUDUT ISTIMEWA Untuk 450 C Sin 450 = 450 1 Cos 450 = 450 Tg 450 = A 1 B

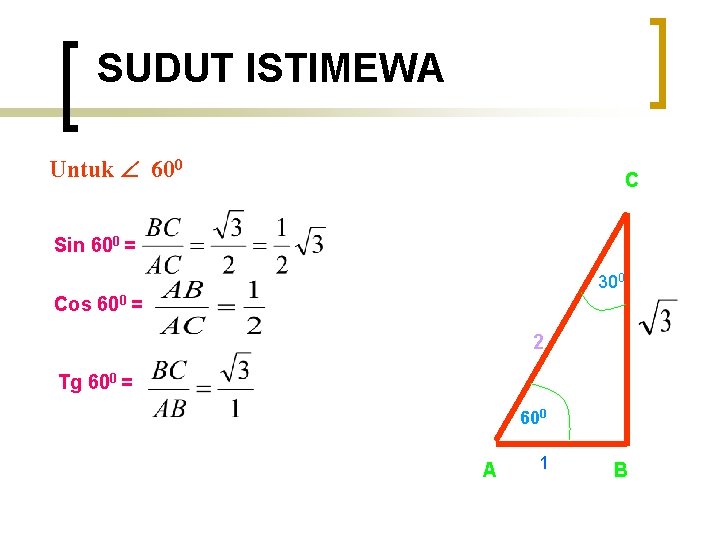
SUDUT ISTIMEWA Untuk 600 C Sin 600 = 300 Cos 600 = 2 Tg 600 = 600 A 1 B

SUDUT ISTIMEWA Untuk 900 Klik salah satu gambar di bawah ini!

Silahkan cari nilai dari sin, cos, dan tan dari sudut 90°!

KESIMPULAN SUDUT ISTIMEWA 0 O Sin 0 1 Cos 1 0 Tg 0 1 Ctg 1 0 30 O 45 O 60 O 90 O

Hitunglah hasilnya! a. Sin 30 o + Cos 30 o + Tan 30 o b. 4 Tan 45 o – 2 Cos 60 o + Sin 60 o Jawab : a. Sin 30 o + Cos 30 o + Tan 30 o b. 4 Tan 45 o – 2 Cos 60 o + Sin 60 o

RUMUS-RUMUS TRIGONOMETRI PADA SEGITIGA 1. RUMUS LUAS SEGITIGA Perhatikan segitiga ABC berikut. A b C Luas segitiga ABC adalah Apabila alas segitiga adalah BC = a. t a c B Maka tinggi segitiga dapat dicari sebagai berikut.

2. RUMUS SINUS DAN RUMUS COSINUS Perhatikan segitiga ABC berikut. C b A a. Pada ∆ADC t a Dari (i) dan (ii) diperoleh: c B b. Pada ∆BDC

Rumus Cosinus a. Pada ∆ADC: CD 2 = AC 2 - AD 2 t 2 = b 2 – (b cos α)2 . . . (iii) b. Pada ∆BDC: CD 2 = CB 2 – BD 2 t 2 = a 2 – (c – b cos α)2 . . . (iv)

Dari (iii) dan (iv) diperoleh: a 2 – (c – b cos α)2 = b 2 – b 2 cos 2 α >> a 2 = b 2 – b 2 cos 2 α + (c – b cos α)2 >> a 2 = b 2 – b 2 cos 2 α + c 2 – 2 bc cos α + b 2 cos 2 α >> a 2 = b 2 + c 2 – 2 bc cos α

Secara umum, pda segitig ABC sembarang berlaku rumus sinus dan rumus cosinus sebagai berikut Rumus Sinus Rumus Cosinus a 2 = b 2 + c 2 – 2 bc cos α b 2 = a 2 + c 2 – 2 ac cos β c 2 = a 2 + b 2 – 2 ab cos λ

SOAL-SOAL LATIHAN

CONTOH SOAL : Pada segitiga ABC, diketahui a = 6, b = 4 dan sudut C = 1200 Tentukan panjang c

PENYELESAIAN : c 2 = a 2 + b 2 – 2. a. b. cos C c 2 = (6)2 + (4)2 – 2. (6). (4). cos 1200 c 2 = 36 + 16 – 2. (6). (4). ( – ½ ) c 2 = 52 + 24 c 2 = 76 c =√ 76 = 2√ 19

CONTOH SOAL : Pada segitiga ABC, diketahui c = 6, sudut B = 600 dan sudut C = 450. Tentukan panjang b !

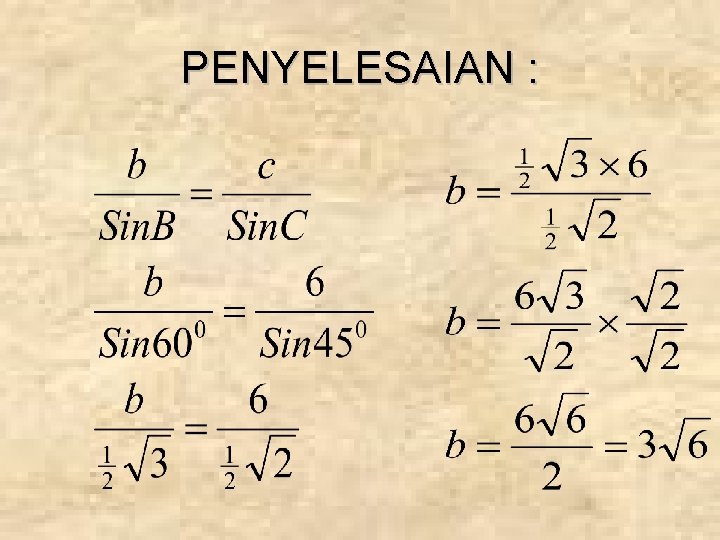
PENYELESAIAN :