TRIGONOMETRI Khabibatul M Siti Wulandari Ilmiawan BU Presented

TRIGONOMETRI

Khabibatul M Siti Wulandari Ilmiawan BU Presented by Den Markindo Syamsul Hadi Indah Tri R

STANDART KOMPETENSI 5. Menggunakan perbandingan, fungsi, persamaan, dan identitas trigonometri dalam pemecahan masalah KOMPETENSI DASAR 5. 1 Melakukan manipulasi aljabar dalam perhitungan teknis yang berkaitan dengan perbandingan, fungsi, persamaan dan identitas trigonometri 5. 2 Merancang model matematika dari masalah yang berkaitan dengan perbandingan, fungsi, persamaan dan identitas trigonometri 5. 3 Menyelesaikan model matematika dari masalah yang berkaitan dengan perbandingan, fungsi, persamaan dan identitas trigonometri, dan penafsirannya

PENGERTIAN TRIGONOMETRI Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

SUB BAB TRIGONOMETRI • SUDUT DAN SATUANNYA • NILAI TRIGONOMETRI SUDUT • IDENTITAS TRIGONOMETRI • RUMUS-RUMUS TRIGONOMETRI PADA SEGITIGA

SUDUT DAN SATUANNYA • Sudut adalah suatu besaran yang dibangun oleh sinar yang diputar dengan pusat perputaran suatu titik tertentu dari suatu posisi awal ke suatu posisi terminal. • Satuan sudut ada dua yaitu : 1. Satuan Derajat 2. Satuan Radian

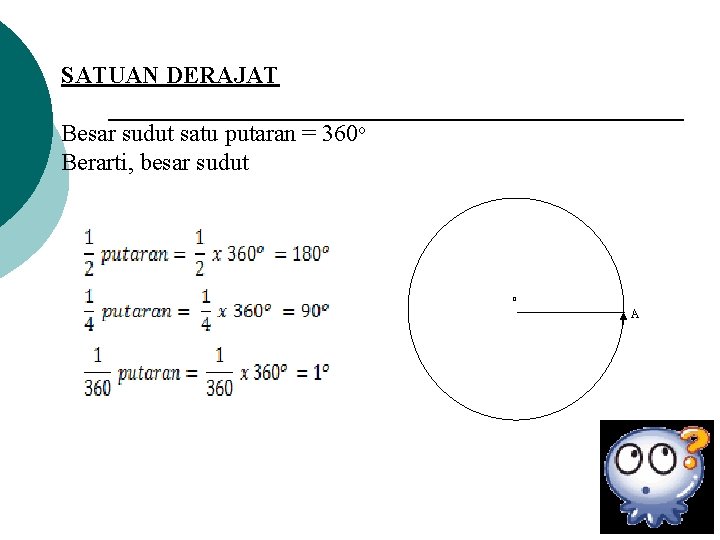
SATUAN DERAJAT Besar sudut satu putaran = 360 o Berarti, besar sudut o A

SATUAN RADIAN Pada lingkaran yang berpusat di O dan berjari-jari r diketahui panjang busur MN sama dengan panjang jari. Besar sudut θ, yaitu sudut pusat lingkarang yang menghadap ke busur MN, didefinisikan sebagai ukuran satu radian. M r o θ r = 1 rad r N

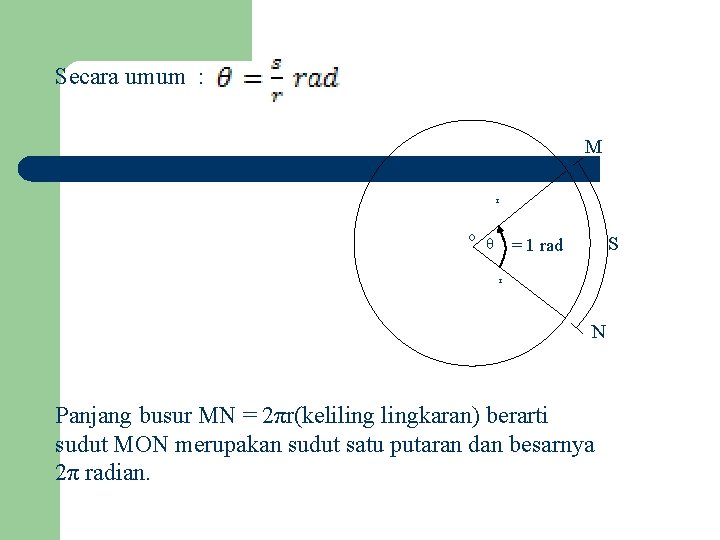
Secara umum : M r o θ S = 1 rad r N Panjang busur MN = 2πr(kelilingkaran) berarti sudut MON merupakan sudut satu putaran dan besarnya 2π radian.

Hubungan satuan derajat dan radian Satuan besar sudut dapat menggunakan derajat atau radian. Kedua satuan itu terdapat hubungan yang menarik. Besar sudut 1 putaran = 360 o Besar sudut 1 putaran = 2π radian 360 o = 2π radian = 360 o ½ putaran → 180 o = π radian ½ putaran → π radian = 180 o

NILAI TRIGONOMETRI SUDUT Perbandingan trigonometri pada segitiga siku-siku Secara umum, pada segitiga siku-siku yang sebangun, perbandingan sisi-sisi menurut salah satu sudutnya bernilai tetap. Perbandingan antara sepanjang sisi pada segitiga siku yang sebangun itulah yang disebut perbandingan C trigonometri. Miring Depan α A B

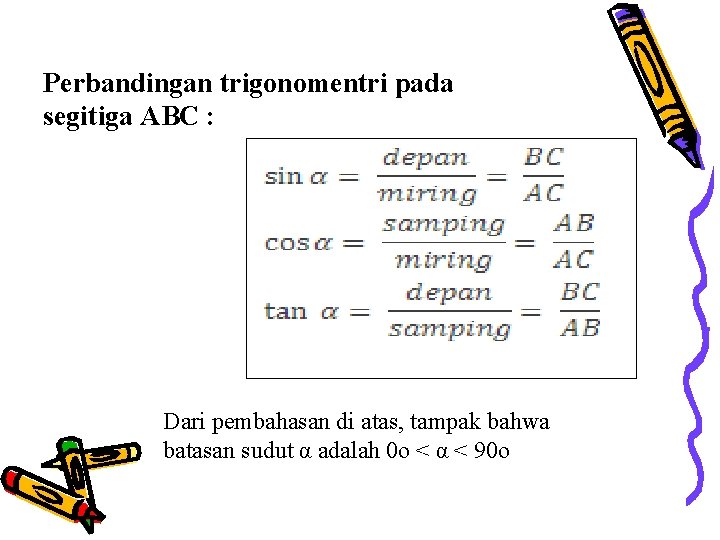
Perbandingan trigonomentri pada segitiga ABC : Dari pembahasan di atas, tampak bahwa batasan sudut α adalah 0 o < α < 90 o

SUDUT PENYIKU Segitiga ABC siku-siku di B A + B + C = 180 o α + 90 o + β = 180 o α+β = 90 o – α jadi, β merupakan sudut penyiku α. C β α A B

PERBANDINGAN TRIGONOMETRI PADA SEGITIGA DALAM SUMBU KARTESIUS Sb y 1. Sinus = y r 2. Cosinus = 3. Tangan = x Sb x

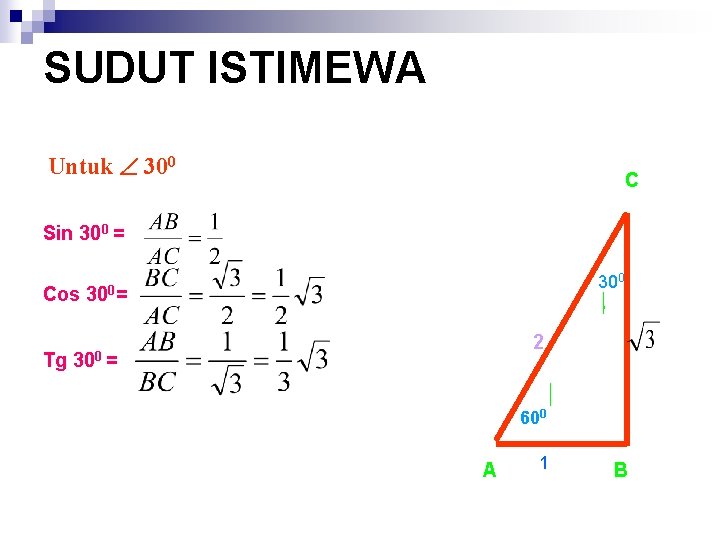
SUDUT ISTIMEWA Untuk 300 C Sin 300 = Cos Tg 300= 2 300 = 600 A 1 B

SUDUT ISTIMEWA Untuk 450 C Sin 450 = 450 1 Cos 450 = 450 Tg 450 = A 1 B

SUDUT ISTIMEWA Untuk 600 C Sin 600 = 300 Cos 600 = 2 Tg 600 = 600 A 1 B

KESIMPULAN SUDUT ISTIMEWA 0 O Sin 0 1 Cos 1 0 Tg 0 1 Ctg 1 0 30 O 45 O 60 O 90 O

Hitunglah hasilnya! a. Sin 30 o + Cos 30 o + Tan 30 o b. 4 Tan 45 o – 2 Cos 60 o + Sin 60 o Jawab : a. Sin 30 o + Cos 30 o + Tan 30 o b. 4 Tan 45 o – 2 Cos 60 o + Sin 60 o

PERBANDINGAN TRIGONOMETRI DI BERBAGAI KUADRAN Sudut di Kuadran I = Sin bernilai (+) Cos bernilai (+) Tan bernilai (+) Sudut di Kuadran II = β = (180 - ) Hanya Sin bernilai (+) Sudut di Kuadran III =γ =(180 + ) Hanya Tan bernilai (+) Sudut di Kuadran IV =θ =( 360 - ) Hanya Cos bernilai (+)

Sudut di Kuadran I Sin �= ( bernilai positif ) Cos �= ( bernilai positif ) Tan �= ( bernilai positif ) Sin ( 90 - � )° = = cos � Cos ( 90 - � )° = = sin � Tan ( 90 - � )° = = cotan �

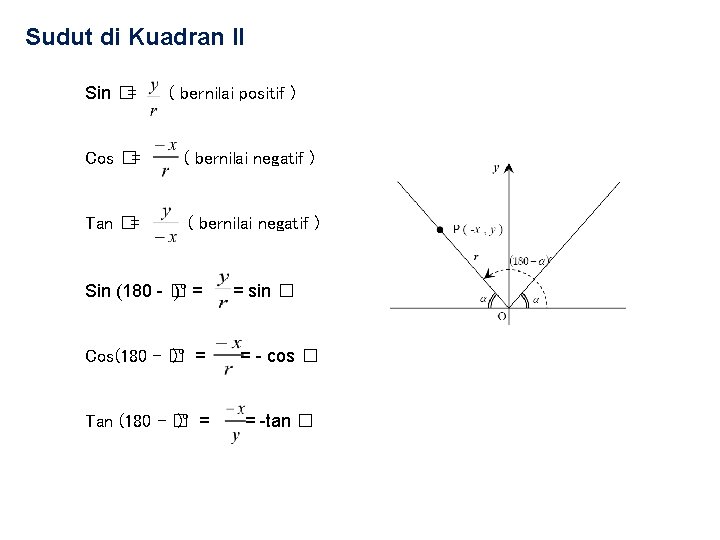
Sudut di Kuadran II Sin �= ( bernilai positif ) Cos �= ( bernilai negatif ) Tan �= ( bernilai negatif ) Sin (180 - � )° = = sin � Cos(180 - � )° = = - cos � Tan (180 - � )° = = -tan �

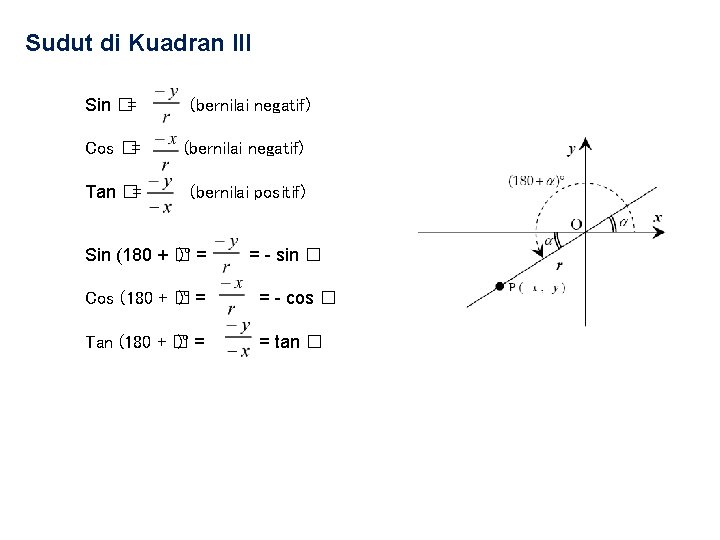
Sudut di Kuadran III Sin �= (bernilai negatif) Cos �= (bernilai negatif) Tan �= (bernilai positif) Sin (180 + � )° = = - sin � Cos (180 + � )° = = - cos � Tan (180 + � )° = = tan �

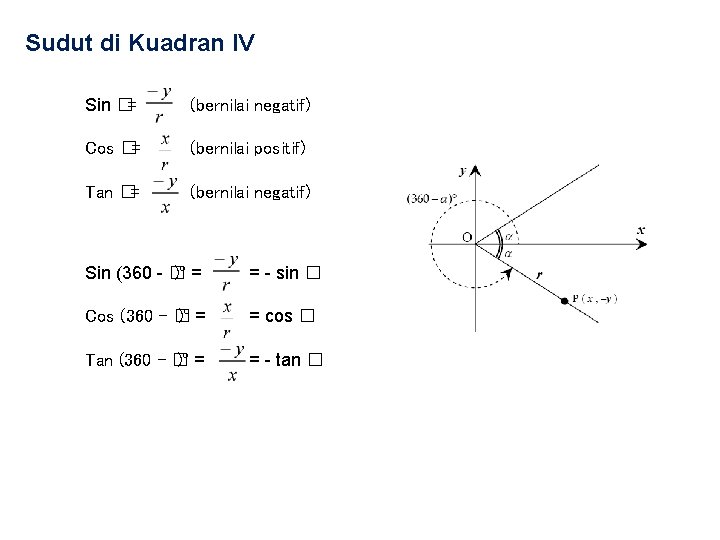
Sudut di Kuadran IV Sin �= (bernilai negatif) Cos �= (bernilai positif) Tan �= (bernilai negatif) Sin (360 - � )° = = - sin � Cos (360 - � )° = = cos � Tan (360 - � )° = = - tan �

Rumus Trigonometri Sudut Yang Lebih Besar dari 360 o atau Sudut Negatif Segitiga siku-siku OPP’ tidak berubah apabila putaran jarum jam OP diputar satu putaran, baik searah putaran jarum jam maupun berlawanan arah jarum jam. Sehingga nilai perbandingan trigonometri sudut α sama dengan nilai perbandingan trigonometri sudut α + k. 360 o di mana k sembarang bilangan bulat positif maupun negative. Jadi, untuk k bilangan bulat berlaku hubungan : Sin α = sin (α + k. 360 o) cos α = cos (α + k. 360 o) tan α = tan (α + k. 360 o)

Hitunglah! Sin 135 o – Cos 225 o + Tan 240 o Jawab : = Sin (180 - 45)o – Cos (180 + 45)o + Tan (180 + 60)o = Sin 45 o – (- Sin 45 o) + Tan 60 o

Identitas Trigonometri

Dua buah fungsi f dan g dikatakan sama identik jika untuk setiap x di mana kedua fungsi didefinisikan. Persamaan seperti di atas disebut suatu identitas.

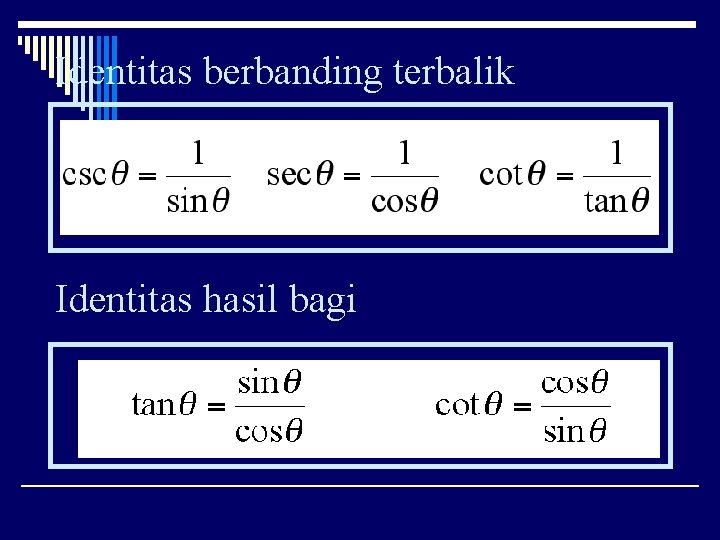
Identitas berbanding terbalik Identitas hasil bagi

Sifat-sifat periodik

Sifat-sifat genap-ganjil

Identitas Pythagoras

Menunjukkan suatu identitas: dengan berdasarkan dasar-dasar identitas dan sejumlah manipulasi aljabar, ditunjukkan bahwa ruas kiri dan ruas kanan suatu identitas adalah sama.

Ditunjukkan identitas :

Ditunjukkan identitas : http: //mediapemb. blogspot. com

Ditunjukkan identitas :

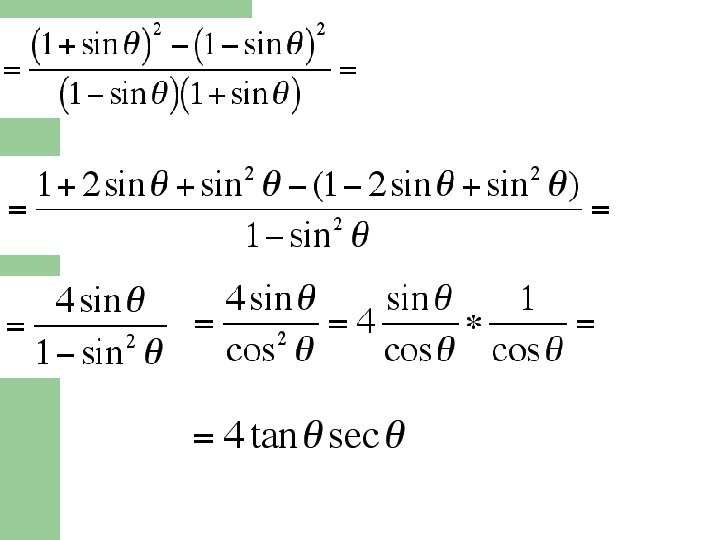
RUMUS-RUMUS TRIGONOMETRI PADA SEGITIGA 1. RUMUS LUAS SEGITIGA Perhatikan segitiga ABC berikut. A b C Luas segitiga ABC adalah Apabila alas segitiga adalah BC = a. t a c B Maka tinggi segitiga dapat dicari sebagai berikut.

2. RUMUS SINUS DAN RUMUS COSINUS Perhatikan segitiga ABC berikut. C b A a. Pada ∆ADC t a Dari (i) dan (ii) diperoleh: c B b. Pada ∆BDC

Rumus Cosinus a. Pada ∆ADC: b. CD 2 = AC 2 - AD 2 c. t 2 = b 2 – (b cos α)2 . . . (iii) b. Pada ∆BDC: CD 2 = CB 2 – BD 2 t 2 = a 2 – (c – b cos α)2 . . . (iv)

Dari (iii) dan (iv) diperoleh: a 2 – (c – b cos α)2 = b 2 – b 2 cos 2 α >> a 2 = b 2 – b 2 cos 2 α + (c – b cos α)2 >> a 2 = b 2 – b 2 cos 2 α + c 2 – 2 bc cos α + b 2 cos 2 α >> a 2 = b 2 + c 2 – 2 bc cos α

Secara umum, pda segitig ABC sembarang berlaku rumus sinus dan rumus cosinus sebagai berikut Rumus Sinus Rumus Cosinus a 2 = b 2 + c 2 – 2 bc cos α b 2 = a 2 + c 2 – 2 ac cos β c 2 = a 2 + b 2 – 2 ab cos λ

SOAL-SOAL LATIHAN

CONTOH SOAL : Pada segitiga ABC, diketahui a = 6, b = 4 dan sudut C = 1200 Tentukan panjang c

PENYELESAIAN : c 2 = a 2 + b 2 – 2. a. b. cos C c 2 = (6)2 + (4)2 – 2. (6). (4). cos 1200 c 2 = 36 + 16 – 2. (6). (4). ( – ½ ) c 2 = 52 + 24 c 2 = 76 c =√ 76 = 2√ 19

CONTOH SOAL : Pada segitiga ABC, diketahui c = 6, sudut B = 600 dan sudut C = 450. Tentukan panjang b !

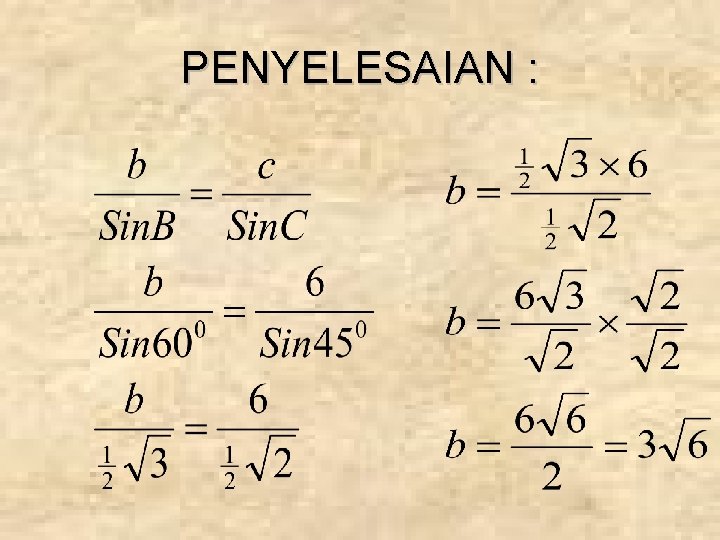
PENYELESAIAN :