Tercer trimestre Ingeniero en Computacin Unidad de aprendizaje







































































- Slides: 92

Tercer trimestre Ingeniero en Computación Unidad de aprendizaje: Álgebra

Competencias El alumno interpreta y aplica los conocimientos de Álgebra lineal mediante procesos y herramientas computacionales para resolver problemas del área con una actitud crítica, responsable y de respeto hacia sus compañeros. 12/03/2021 Página 2

Contenido 1. Conceptos preliminares 2. Números complejos 3. Polinomios 4. Matrices y determinantes 5. Espacios vectoriales 6. Transformaciones lineales 12/03/2021 Página 3

Bibliografía básica 1. Lehmann, Charles (2006). Álgebra. Editorial Limusa. 2. Uspensky, J. V. (1995). Teoría de ecuaciones. Editorial Limusa. México. 3. Anton, Howard (2008). Introducción al Álgebra Lineal. Editorial Limusa. México. 4. Grossman, Stanley I. (2007). Algebra Lineal. Editorial Mc. Graw Hill. 5. Larson, Ron y Falvo, David C. (2010). Fundamentos de Álgebra Lineal. Editorial CENGAGE. 6. Cantoral, Ricardo y otros (2003). Desarrollo del pensamiento matemático. Editorial Trillas. 12/03/2021 Página 4

http: //www. sectormatematica. cl/libros. htm 12/03/2021 Página 5

Evaluación Unidad 1 y 2 3 y 4 5 y 6 Examen Primer parcial Segundo parcial Tercer parcial Evaluación diaria Examen final Calificación 40% 9 exento 60%

Reglamento escolar Artículo 48. Los exámenes parciales se aplicarán en las fechas acordadas entre profesor y estudiantes, en el aula correspondiente, sin suspensión del resto de las clases y dentro del horario de funcionamiento de la Unidad Académica. El estudiante que obtenga un promedio de nueve, tendrá derecho a exentar el examen final. Artículo 49. Las evaluaciones finales se aplicarán en las fechas establecidas en el calendario escolar aprobado por el H. Consejo Universitario, en las instalaciones de las unidades académicas y en los horarios fijados por las mismas.

Artículo 50. Sólo tendrá derecho a presentar examen final, el estudiante cuya asistencia a clases no sea menor a ochenta por ciento. Para hacer efectiva esta disposición, el académico deberá llevar el control de asistencias. Artículo 51. Los exámenes finales, con la excepción de talleres y prácticas de laboratorio, siempre serán escritos, y el material de evaluación consistirá en el contenido total de la unidad de aprendizaje. Serán elaborados por el cuerpo de académicos del área de la academia que imparta la unidad de aprendizaje. Cuando el estudiante no haya reprobado ningún examen parcial o el promedio de las evaluaciones parciales no sea inferior a ocho, tendrá derecho a que si obtiene en la evaluación final una calificación superior a las evaluaciones parciales, ésta será la calificación definitiva que se reporte.

Aplicación de algunas nomenclaturas para reporte de calificaciones NA (No acreditada): A quienes no se hayan presentado al examen parcial o final y tengan una asistencia del 60%, ellos tienen derecho a presentar el examen extraordinario o a recursarla. NC (No cursada): Cuando el alumno no se presentó a clases, presentando la solicitud por escrito de acuerdo a los tiempos establecidos en el calendario escolar y: a) Podrá cursar la unidad de aprendizaje b) No podrá presentar examen extraordinario SD (Sin derecho): Cuando el alumno no se presentó a clases, o se presentó menos del 60%, deberá recursar la unidad de aprendizaje. De acuerdo con al art. 58 inciso c del Reglamento Escolar vigente.

1. Conceptos preliminares 12/03/2021 Página 10

Teoría de conjuntos Rama de las matemáticas que estudia las propiedades de los conjuntos. Los conjuntos son colecciones abstractas de objetos, consideradas como objetos en sí mismas, y son una herramienta básica en la formulación de cualquier teoría matemática. La teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, etc. , y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática. La propia teoría de conjuntos es objeto de estudio por sí misma, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. 12/03/2021 Página 11

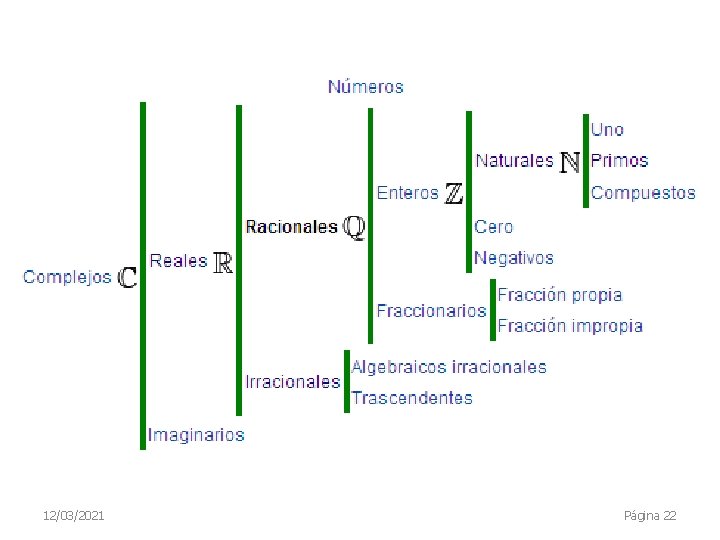
Un conjunto es una colección de objetos considerada como un objeto en sí. Los objetos de la colección pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Pueden ser finitos o infinitos Cada uno de los objetos en la colección es un elemento o miembro del conjunto. Ejemplo, el conjunto de los colores del arcoíris: A = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta} Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, los números naturales. 12/03/2021 Página 12

12/03/2021 Página 13

Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que utilizó el ser humano para contar objetos. Otro conjunto: Los números primos P = {2, 3, 5, 7, 11, 13, . . . } Un número primo es un número natural mayor que 1 que tiene únicamente dos divisores distintos: él mismo la unidad y sus respectivos opuestos. Conjunto de los números compuestos. 12/03/2021 Página 14

Conjunto de los números racionales Número racional es todo número que puede representarse como el cociente de dos números enteros, es decir, una fracción común a/b con numerador a y denominador b distinto de cero. El término racional alude a fracción o parte de un todo. El conjunto de los números racionales se denota por Q (o bien , en Blackboard bold) que deriva de «cociente» (Quotient en varios idiomas europeos). Fracción propia Fracción impropia 12/03/2021 Página 15

Número irracional Es cualquier número real que no es racional, es decir, es un número que no puede ser expresado como una fracción, y que expresados como números decimales no están compuestos por ningún periodo 12/03/2021 Página 16

Números decimales Se denominan números decimales aquellos que poseen una parte decimal, en oposición a los números enteros que carecen de ella. Número decimal exacto Son los números decimales cuya parte decimal tiene un número finito de cifras. Los números enteros pertenecen a este conjunto. Se pueden escribir como fracción, y por tanto, pertenecen a un subconjunto de los números racionales. 12/03/2021 Página 17

Número decimal periódico Son los números cuya parte decimal tiene un número infinito de cifras que se repiten siguiendo un patrón, llamado periodo. Decimal periódico puro Son los números decimales en los que la parte decimal se repite periódicamente, inmediatamente después del separador decimal. La parte periódica se suele señalar usualmente con una línea horizontal superior. 0. 33333 12/03/2021 0. 3 Página 18

Decimal periódico mixto Son los números decimales en cuya parte decimal hay una parte no periódica, denominada antiperiodo, y otra periódica. La parte periódica se suele señalar con una línea horizontal superior. 0. 1666 0. 16 Al igual que los números decimales periódicos puros, los números decimales mixtos siempre pueden ser expresados en forma de fracción; en el caso del ejemplo, la fracción equivalente es 1/6 12/03/2021 Página 19

Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, . . . ), los negativos de los números naturales (. . . , − 3, − 2, − 1) y al cero, 0. Los enteros negativos, como − 1 ó − 3, son menores que todos los enteros positivos (1, 2, . . . ) y que el cero. Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo «más» delante de los positivos: +1, +5, etc. Cuando no se le escribe signo al número se asume que es positivo. El conjunto de todos los números enteros se representa por la letra ℤ = {. . . , . . . }, que proviene del alemán Zahlen (números) 12/03/2021 Página 20

12/03/2021 Página 21

12/03/2021 Página 22

Existen dos maneras de describir o especificar los elementos de un conjunto: Por definición intensiva o comprensión: Se hace una descripción de una condición que cumplen sus elementos: A es el conjunto cuyos miembros son los números enteros positivos menores que 5. B es el conjunto de colores de la bandera de México. Por extensión: Listando cada miembro del conjunto en una definición extensiva se escriben los elementos del conjunto entre llaves: C = {4, 2, 3, 1} D = {blanco, rojo, verde} 12/03/2021 Página 23

Otra notación habitual para denotar por comprensión es: A = {m : m es un entero, y 1 ≤ m ≤ 5} B = {c : c es un color de la bandera de México} F = {n 2 : n es un entero y 1 ≤ n ≤ 10} , 12/03/2021 Página 24

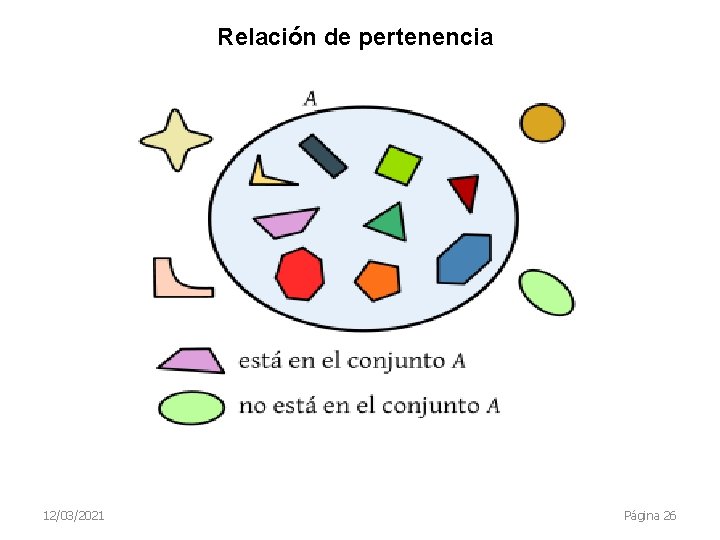
La relación clave en un conjunto es la pertenencia: Cuándo es un elemento miembro de un conjunto. Si a es un miembro de B, se denota por a ∈ B, y si no lo es, se denota por a ∉ B. Por ejemplo: respecto a los conjuntos A, B y F de la lámina anterior: 4 ∈ A , 36 ∈ F , verde ∈ B 7 ∉ A , 8 ∉ F , azul ∉ B Se dice entonces que 4 pertenece al conjunto A, 4 es un miembro de A, 4 está en A o A contiene a 4. 12/03/2021 Página 25

Relación de pertenencia 12/03/2021 Página 26

Los conjuntos pueden ser finitos o infinitos. En un conjunto finito podemos contar sus elementos. El número de elementos de un conjunto finito es su cardinal. El cardinal se denota por |A|, card(A) o #A. En los ejemplos anteriores, se tiene que; |A| = 4 (cuatro números), |B| = 3 (tres colores) y |F| = 10 (diez cuadrados). El único conjunto cuyo cardinal es 0 es el conjunto vacío ∅. 12/03/2021 Página 27

12/03/2021 Página 28

12/03/2021 Página 29

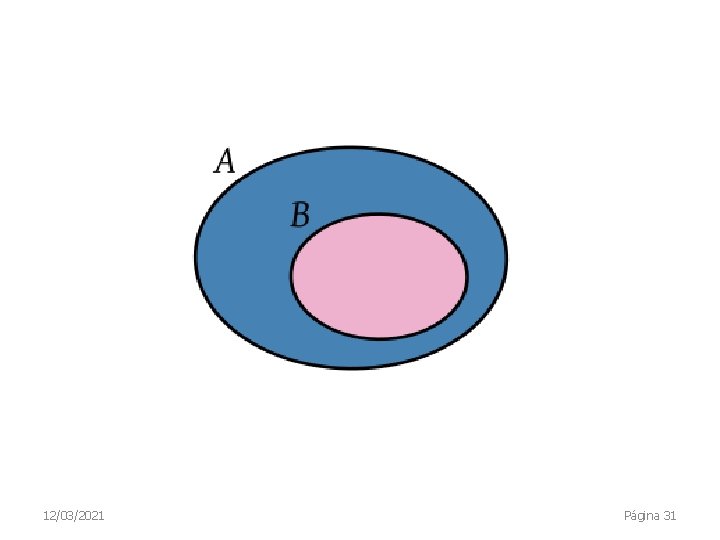
Subconjuntos Un subconjunto A de un conjunto B, es un conjunto que contiene algunos o todos los elementos de B: Un conjunto A es un subconjunto del conjunto B si cada elemento de A es a su vez un elemento de B Si A es un subconjunto de B, se escribe como A ⊆ B y se dice que «A está contenido en B» . También puede escribirse B ⊇ A, y decirse que B es un superconjunto de A y también «B contiene a A» o «B incluye a A» . Si A no sólo contiene algunos sino todos los elementos de B, A no sólo es un subconjunto de B, sino que ambos conjuntos son iguales, A = B. 12/03/2021 Página 30

12/03/2021 Página 31

El otro caso posible es que A contenga algunos pero no todos los elementos de B: A es un subconjunto de B pero no son iguales. Se dice entonces que A es un subconjunto propio de B y se denota A ⊊ B, es decir: A ⊆ B pero A ≠ B (y equivalentemente, para un superconjunto propio, B ⊋ A). También se utiliza la notación A ⊂ B y B ⊃ A 12/03/2021 Página 32

12/03/2021 Página 33

En un conjunto infinito no hay un número finito de elementos. Es el caso por ejemplo de los números naturales: N = {1, 2, 3, . . . }. Sin embargo, los conjuntos infinitos pueden compararse, y resulta que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es un número transfinito. 12/03/2021 Página 34

Operaciones conjuntos Unión La unión de dos conjuntos A y B es el conjunto A∪B que contiene todos los elementos de A y de B. 12/03/2021 Página 35

De la definición de unión puede deducirse directamente: Idempotencia. La unión de un conjunto A consigo mismo es el propio A : A ∪ A = A Tanto A como B son subconjuntos de su unión: A ⊆ A ∪ B y B ⊆ A ∪ B La unión de un conjunto A con un subconjunto suyo B lo deja inalterado: B ⊆ A implica que A ∪ B = A 12/03/2021 Página 36

La unión de conjuntos posee también propiedades similares a las operaciones con números: Propiedad asociativa La unión de los conjuntos A y B ∪ C es igual que la unión de los conjuntos A ∪ B y C : (A ∪ B) ∪ C = A ∪ (B ∪ C) 12/03/2021 Página 37

Propiedad conmutativa La unión de los conjuntos A y B es igual a la unión de los conjuntos B y A: A ∪ B = B ∪ A 12/03/2021 Página 38

Elemento neutro La unión de un conjunto A con el conjunto vacío es el mismo conjunto A: A ∪ ∅ = A 12/03/2021 Página 39

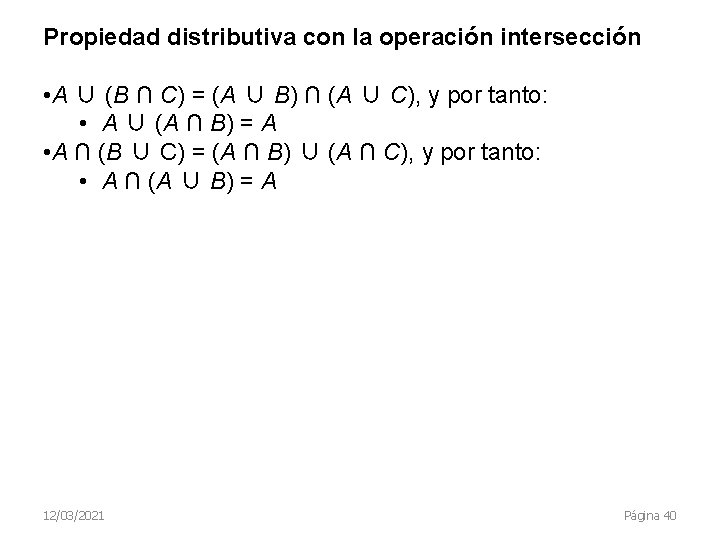
Propiedad distributiva con la operación intersección • A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: • A ∪ (A ∩ B) = A • A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: • A ∩ (A ∪ B) = A 12/03/2021 Página 40

12/03/2021 Página 41

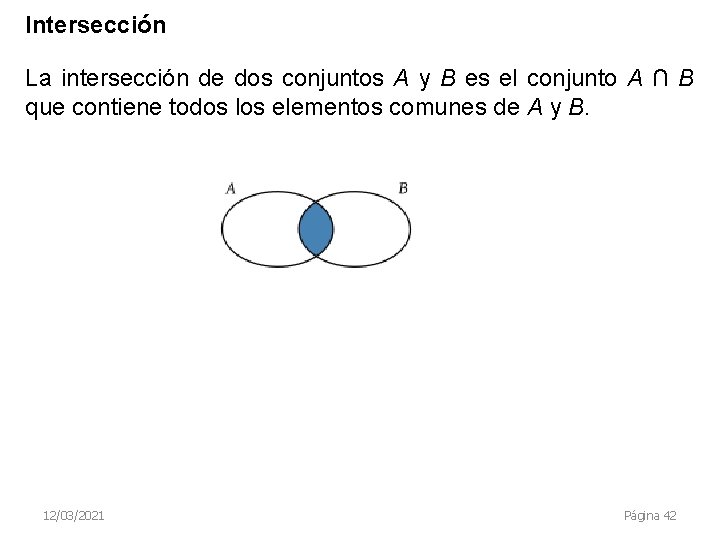
Intersección La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B. 12/03/2021 Página 42

12/03/2021 Página 43

La intersección de conjuntos posee también propiedades similares a las operaciones con números: Propiedad asociativa La intersección de los conjuntos A y B ∩ C es igual a la intersección de los conjuntos A ∩ B y C : (A ∩ B) ∩ C = A ∩ (B ∩ C) 12/03/2021 Página 44

Propiedad conmutativa La intersección de los conjuntos A y B es igual a la intersección de los conjuntos B y A : A ∩ B = B ∩ A 12/03/2021 Página 45

Elemento absorbente La intersección de un conjunto A con el conjunto vacío ∅ es ∅: A ∩ ∅ = ∅ 12/03/2021 Página 46

Propiedad distributiva con la operación unión • A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), y por tanto: • A ∪ (A ∩ B) = A • A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), y por tanto: • A ∩ (A ∪ B) = A 12/03/2021 Página 47

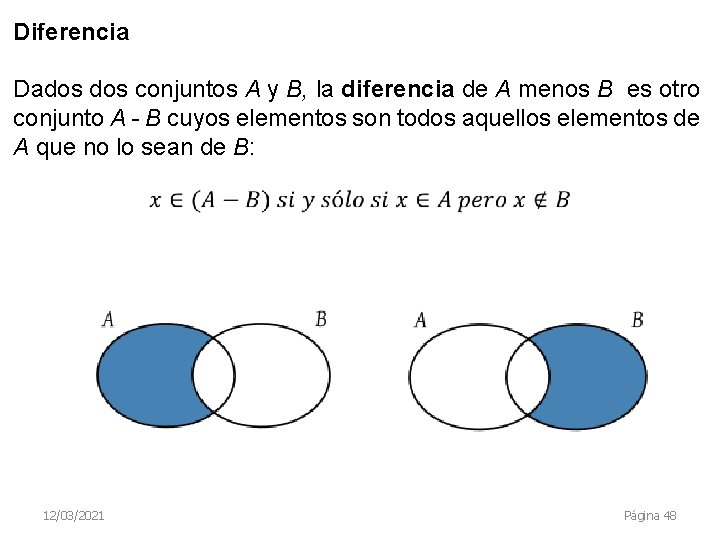
Diferencia Dados conjuntos A y B, la diferencia de A menos B es otro conjunto A - B cuyos elementos son todos aquellos elementos de A que no lo sean de B: 12/03/2021 Página 48

Elemento neutro La diferencia entre un conjunto y el conjunto vacío es el propio conjunto: A − ∅ = A La diferencia de un conjunto menos él mismo es el conjunto vacío: A − A = ∅ 12/03/2021 Página 49

La diferencia entre dos conjuntos es el conjunto vacío si y sólo si el primero es un subconjunto del segundo: A − B = ∅ si y sólo si A ⊆ B La diferencia entre dos conjuntos es igual al primer conjunto si sólo si ambos conjuntos son disjuntos: A − B = A si y sólo si A ∩ B = ∅ 12/03/2021 Página 50

La intersección de dos conjuntos es la parte que tienen en común, mientras que la diferencia es la parte que no comparten. Esto se traduce en la siguiente propiedad: Dados conjuntos, su intersección y su diferencia son disjuntos entre sí, pero su unión es el primero de los conjuntos iniciales: (A ∩ B) ∩ (A - B) = ∅, pero (A ∩ B) ∪ (A - B) = A Esto quiere decir que la intersección y la diferencia entre A y B son una posible partición de A. 12/03/2021 Página 51

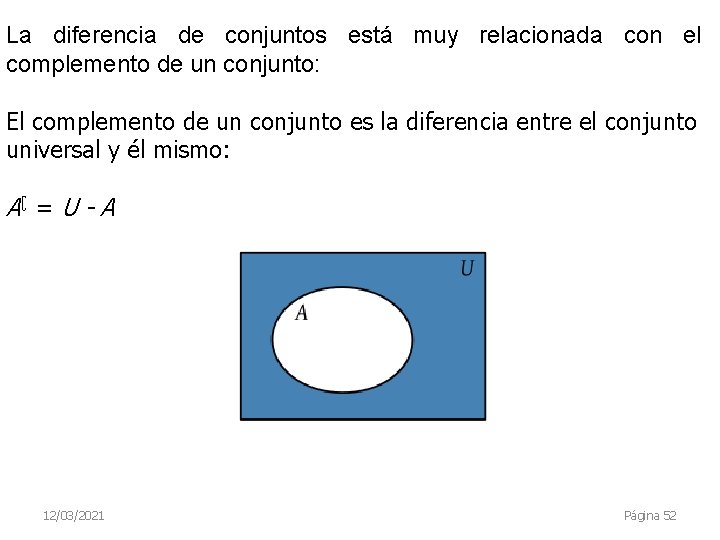
La diferencia de conjuntos está muy relacionada con el complemento de un conjunto: El complemento de un conjunto es la diferencia entre el conjunto universal y él mismo: A∁ = U - A 12/03/2021 Página 52

Producto cartesiano El producto cartesiano de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par del primer conjunto, y el segundo elemento del segundo conjunto. Ejemplo: Dados los conjuntos A = {1, 2, 3, 4} B = {a, b} Su producto cartesiano es: A × B = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b), (4, a), (4, b)} 12/03/2021 Página 53

. 12/03/2021 Página 54

12/03/2021 Página 55

12/03/2021 Página 56

12/03/2021 Página 57

Ejercicios 1. Enlístense las relaciones del ejemplo 5. 2. Diga cuál es el dominio en cada una de las dieciséis relaciones en el ejercicio anterior. 3. Diga cuál es la imagen en cada una de las relaciones del ejemplo 5. 4. En el ejemplo 5 indique cuáles relaciones tienen la propiedad de que su imagen y su codominio coinciden. 12/03/2021 Página 58

12/03/2021 Página 59

12/03/2021 Página 60

12/03/2021 Página 61

12/03/2021 Página 62

12/03/2021 Página 63

Representación de las relaciones Como tabulación: tabla que permite representar algunos valores discretos de la función. 12/03/2021 Página 64

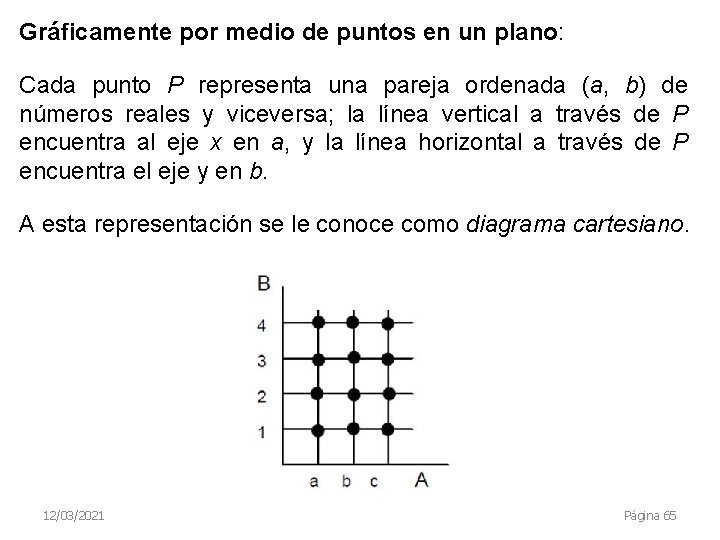
Gráficamente por medio de puntos en un plano: Cada punto P representa una pareja ordenada (a, b) de números reales y viceversa; la línea vertical a través de P encuentra al eje x en a, y la línea horizontal a través de P encuentra el eje y en b. A esta representación se le conoce como diagrama cartesiano. 12/03/2021 Página 65

Diagrama de flechas Se dibujan los puntos que pertenecen a A y los que pertenecen a B. Se trazan flechas que indican la relación que existe entre cada elemento del conjunto A y su correspondiente en el conjunto B. 12/03/2021 Página 66

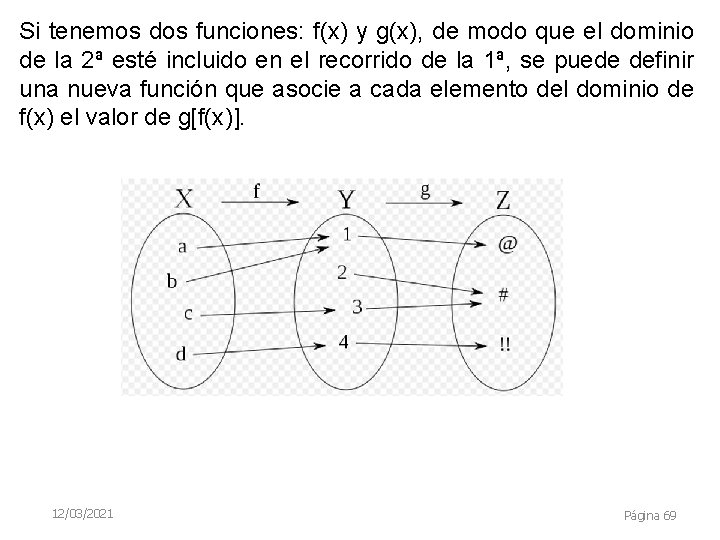
Composición de funciones Dadas dos funciones f: X → Y y g: Y → Z, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ∘ f ): X → Z como (g ∘ f)(x) = g (f(x)), para todos los elementos x de X. O de manera gráfica mediante un diagrama conmutativo: 12/03/2021 Página 67

12/03/2021 Página 68

Si tenemos dos funciones: f(x) y g(x), de modo que el dominio de la 2ª esté incluido en el recorrido de la 1ª, se puede definir una nueva función que asocie a cada elemento del dominio de f(x) el valor de g[f(x)]. 12/03/2021 Página 69

12/03/2021 Página 70

12/03/2021 Página 71

12/03/2021 Página 72

12/03/2021 Página 73

12/03/2021 Página 74

Propiedades Asociativa: f o (g o h) = (f o g) o h No es conmutativa. fog≠gof El elemento neutro es la función identidad, i(x) = x. f o i = i o f = f 12/03/2021 Página 75

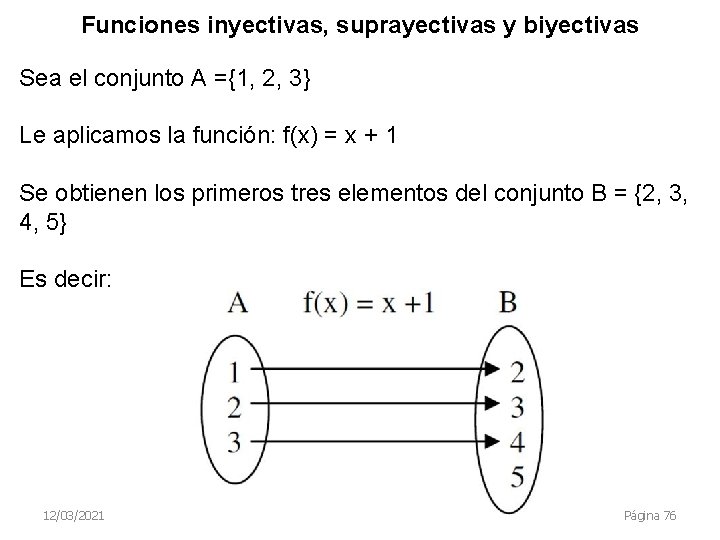
Funciones inyectivas, suprayectivas y biyectivas Sea el conjunto A ={1, 2, 3} Le aplicamos la función: f(x) = x + 1 Se obtienen los primeros tres elementos del conjunto B = {2, 3, 4, 5} Es decir: 12/03/2021 Página 76

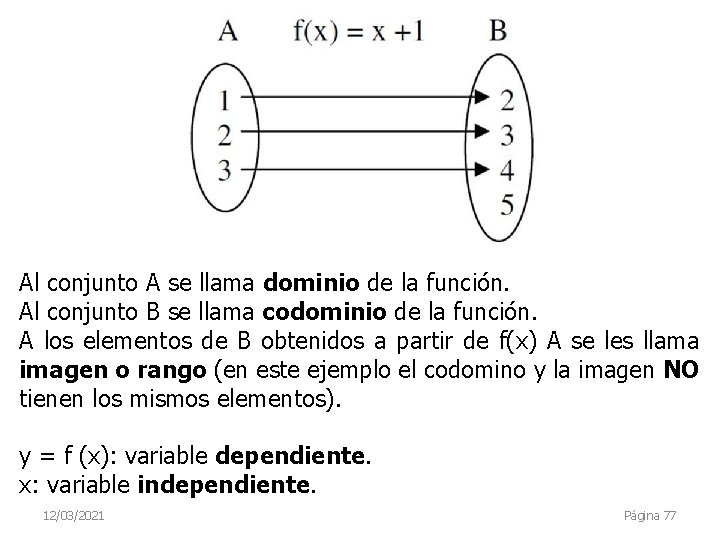
Al conjunto A se llama dominio de la función. Al conjunto B se llama codominio de la función. A los elementos de B obtenidos a partir de f(x) A se les llama imagen o rango (en este ejemplo el codomino y la imagen NO tienen los mismos elementos). y = f (x): variable dependiente. x: variable independiente. 12/03/2021 Página 77

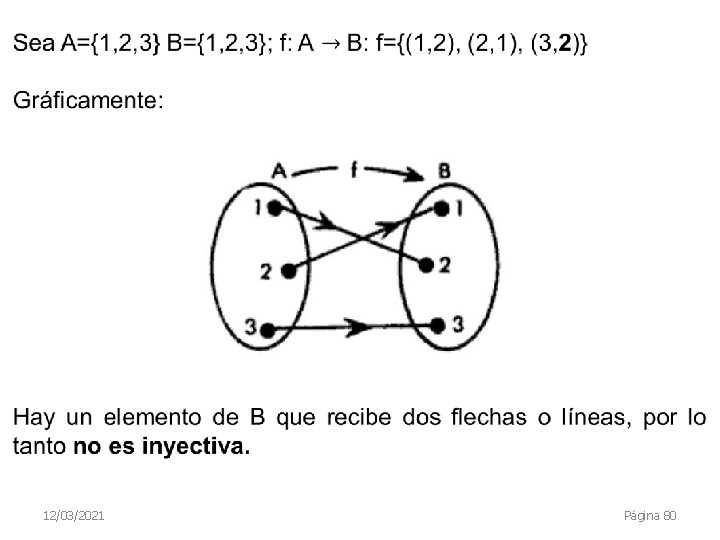
La función del ejemplo anterior también lo podemos indicar definiendo los conjuntos A y B; y posteriormente definir la función; es decir: A = {1, 2, 3} B = {2, 3, 4, 5} f = {(1, 2), (2, 3), (3, 4)} 12/03/2021 Página 78

12/03/2021 Página 79

12/03/2021 Página 80

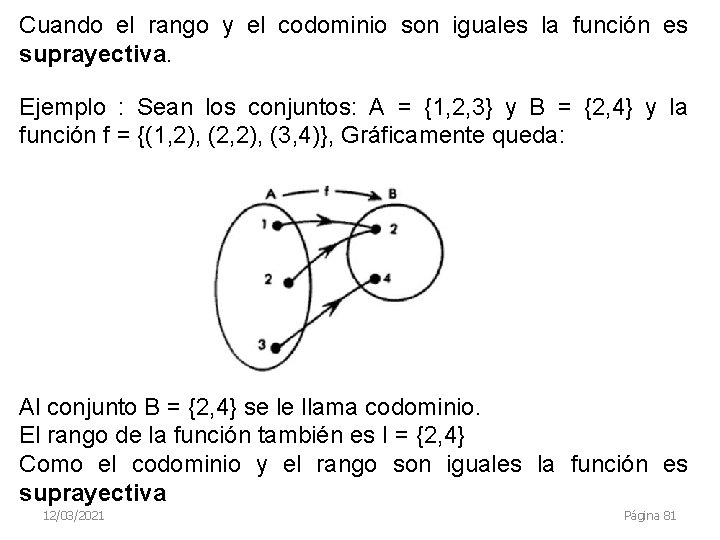
Cuando el rango y el codominio son iguales la función es suprayectiva. Ejemplo : Sean los conjuntos: A = {1, 2, 3} y B = {2, 4} y la función f = {(1, 2), (2, 2), (3, 4)}, Gráficamente queda: Al conjunto B = {2, 4} se le llama codominio. El rango de la función también es I = {2, 4} Como el codominio y el rango son iguales la función es suprayectiva 12/03/2021 Página 81

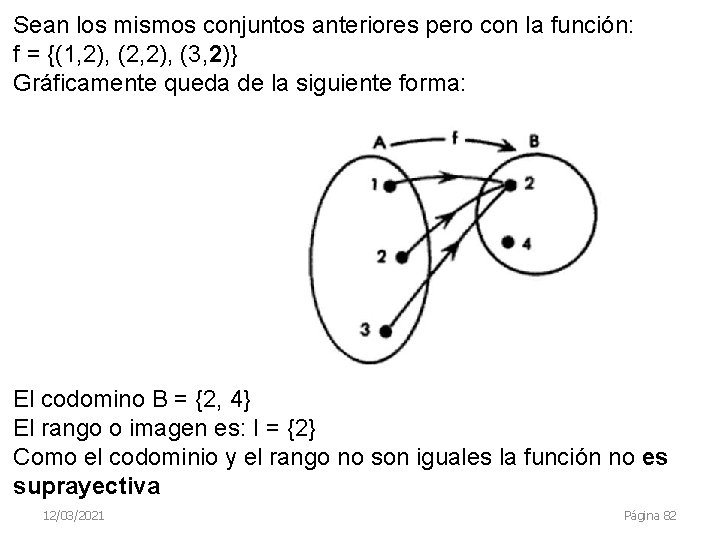
Sean los mismos conjuntos anteriores pero con la función: f = {(1, 2), (2, 2), (3, 2)} Gráficamente queda de la siguiente forma: El codomino B = {2, 4} El rango o imagen es: I = {2} Como el codominio y el rango no son iguales la función no es suprayectiva 12/03/2021 Página 82

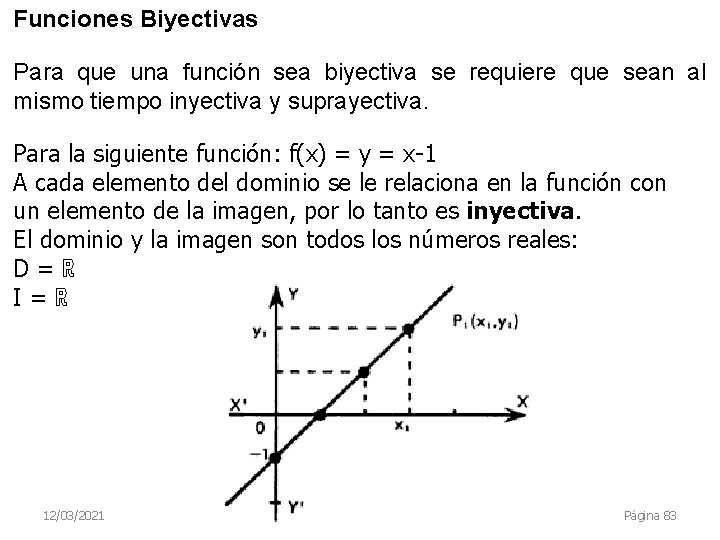
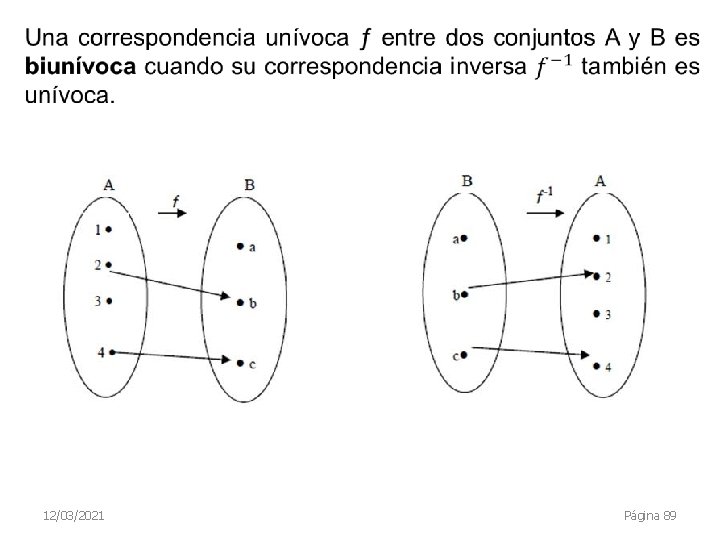
Funciones Biyectivas Para que una función sea biyectiva se requiere que sean al mismo tiempo inyectiva y suprayectiva. Para la siguiente función: f(x) = y = x-1 A cada elemento del dominio se le relaciona en la función con un elemento de la imagen, por lo tanto es inyectiva. El dominio y la imagen son todos los números reales: D = ℝ I = ℝ 12/03/2021 Página 83

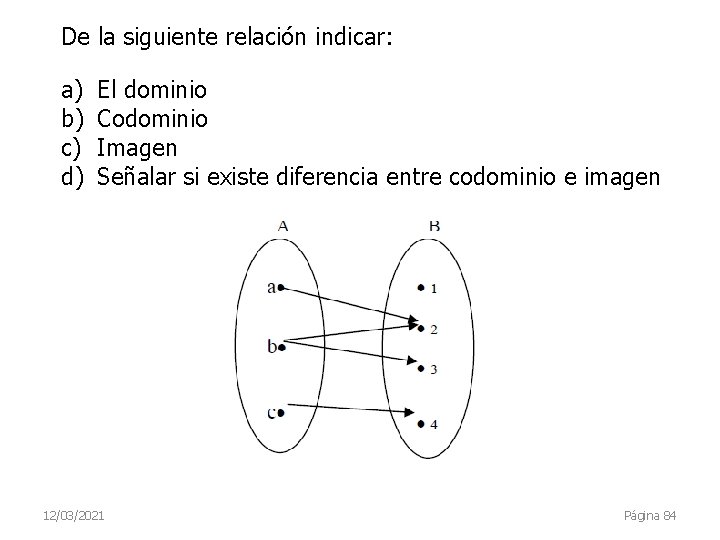
De la siguiente relación indicar: a) b) c) d) El dominio Codominio Imagen Señalar si existe diferencia entre codominio e imagen 12/03/2021 Página 84

12/03/2021 Página 85

12/03/2021 Página 86

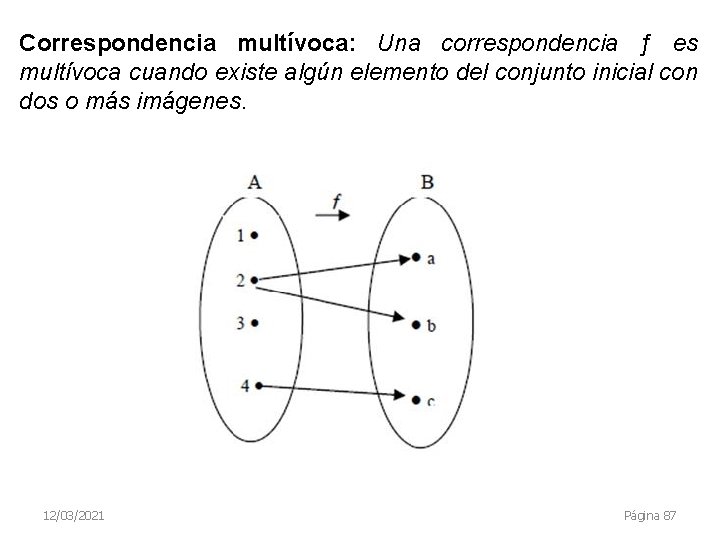
Correspondencia multívoca: Una correspondencia ƒ es multívoca cuando existe algún elemento del conjunto inicial con dos o más imágenes. 12/03/2021 Página 87

12/03/2021 Página 88

12/03/2021 Página 89

12/03/2021 Página 90

12/03/2021 Página 91

12/03/2021 Página 92
 Computacin
Computacin Computacin
Computacin Computacin
Computacin Computacin
Computacin Estimulo incondicionado
Estimulo incondicionado Unidad de aprendizaje curricular
Unidad de aprendizaje curricular Unidad de mil
Unidad de mil Ebd 1 trimestre 2019
Ebd 1 trimestre 2019 Mapa da trajetória do povo de israel no deserto
Mapa da trajetória do povo de israel no deserto 30 ejemplos de acento diacrítico
30 ejemplos de acento diacrítico Cuadro de honor segundo trimestre
Cuadro de honor segundo trimestre 2019 em romano
2019 em romano Ebd 1 trimestre 2019
Ebd 1 trimestre 2019 Placenta previa
Placenta previa Ebd 1 trimestre 2019
Ebd 1 trimestre 2019 Juanes biografia
Juanes biografia Objetivos de la ingenieria industrial
Objetivos de la ingenieria industrial Perro ingeniero
Perro ingeniero Habilidades de un ingeniero industrial
Habilidades de un ingeniero industrial Cuasi ingeniero
Cuasi ingeniero Regulacion profesion ingeniero industrial
Regulacion profesion ingeniero industrial Valores de ingenieria civil
Valores de ingenieria civil Manejo activo del tercer periodo
Manejo activo del tercer periodo El tercer elias
El tercer elias Disocoria
Disocoria Hito 31 de mayo schoenstatt
Hito 31 de mayo schoenstatt Cual es el tercer continente mas grande
Cual es el tercer continente mas grande Quejoso amparo
Quejoso amparo Tercer domingo de adviento ciclo c
Tercer domingo de adviento ciclo c Hbito
Hbito Tercer domingo de adviento ciclo c
Tercer domingo de adviento ciclo c Hola
Hola Uso frecuente
Uso frecuente Tercer bimestre animado
Tercer bimestre animado Tercer estado de conciencia gnosis
Tercer estado de conciencia gnosis Oracion del tercer paso
Oracion del tercer paso Tercer parcial
Tercer parcial Cantos tercer domingo de cuaresma ciclo c
Cantos tercer domingo de cuaresma ciclo c Tercer viaje misionero de pablo powerpoint
Tercer viaje misionero de pablo powerpoint Ejemplo de preguntas cerradas
Ejemplo de preguntas cerradas Sexto mes del calendario judio
Sexto mes del calendario judio Cuarto bimestre matemáticas
Cuarto bimestre matemáticas Sistema solar y sus planetas
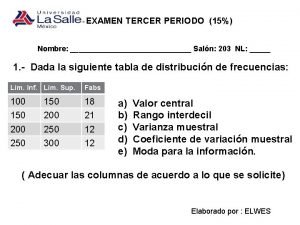
Sistema solar y sus planetas Examen tercer periodo
Examen tercer periodo Moniciones cuarto domingo de adviento ciclo c
Moniciones cuarto domingo de adviento ciclo c Color 271118
Color 271118 Tercer cuadrante del sistema coordenado rectangular
Tercer cuadrante del sistema coordenado rectangular Chistes de di casa
Chistes de di casa Tercer organizador de spitz
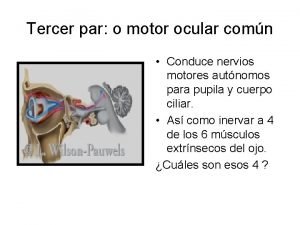
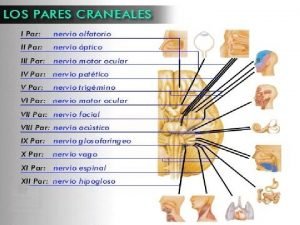
Tercer organizador de spitz Origen tercer par craneal
Origen tercer par craneal Tercer bimestre animado
Tercer bimestre animado Página 128 de español tercer grado
Página 128 de español tercer grado Marcos de tercer periodo
Marcos de tercer periodo Tercer mandamiento
Tercer mandamiento Primero segundo, tercero cuarto
Primero segundo, tercero cuarto Ley de newton
Ley de newton La piramide alimenticia y sus niveles
La piramide alimenticia y sus niveles Descolonización y tercer mundo
Descolonización y tercer mundo Tercer viaje de colón
Tercer viaje de colón Segundo principio de la termodinámica
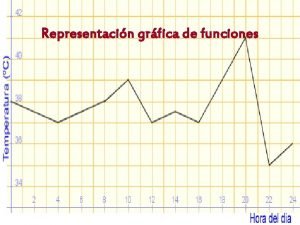
Segundo principio de la termodinámica Funciones lineales
Funciones lineales Discriminación de precios de tercer grado
Discriminación de precios de tercer grado Que es el tercer cielo biblicamente
Que es el tercer cielo biblicamente Multiplicaciones de radicales
Multiplicaciones de radicales 3er lapso
3er lapso Consumidores de tercer orden ejemplos
Consumidores de tercer orden ejemplos Cuarto misterio luminoso
Cuarto misterio luminoso Expresion grafica dibujo tecnico
Expresion grafica dibujo tecnico Características del tercer militarismo
Características del tercer militarismo Formula para cuartiles
Formula para cuartiles Ejemplo de santificar las fiestas
Ejemplo de santificar las fiestas Tulio hostilio rey de roma
Tulio hostilio rey de roma Periodo de los millones
Periodo de los millones Tercer metal que compone los latones especiales
Tercer metal que compone los latones especiales Cuarto presagio funesto lago en llamas
Cuarto presagio funesto lago en llamas Los viajes de pizarro mapa conceptual
Los viajes de pizarro mapa conceptual 1 misterio glorioso
1 misterio glorioso Dame un punto de apoyo
Dame un punto de apoyo Descolonización y tercer mundo
Descolonización y tercer mundo Iso a e iso e
Iso a e iso e Que son los angulos cuadrantales
Que son los angulos cuadrantales Clasificacion de quemaduras por superficie corporal
Clasificacion de quemaduras por superficie corporal Segundo principio de la termodinámica
Segundo principio de la termodinámica Visitación de la virgen maría a su prima isabel
Visitación de la virgen maría a su prima isabel Aprendizaje como proceso
Aprendizaje como proceso Ejemplo de actividad y tarea
Ejemplo de actividad y tarea Importancia del aprendisaje
Importancia del aprendisaje Dimensiones del aprendizaje marzano
Dimensiones del aprendizaje marzano Condicionantes del aprendizaje
Condicionantes del aprendizaje Escala de estrategias de aprendizaje acra
Escala de estrategias de aprendizaje acra Aprendizaje autorregulado
Aprendizaje autorregulado Estrategias de aprendizaje ejemplos
Estrategias de aprendizaje ejemplos Aprendizaje latente y mapas cognitivos
Aprendizaje latente y mapas cognitivos